スロットマシンでもう少し遊ぶ(UCBアルゴリズム)

はじめに

こんにちは。株式会社エイアイ・フィールドでプロダクト開発をしている久保です。この記事はエイアイ・フィールドアドベントカレンダー2021の5日目の記事です。この記事では、多腕バンディット問題について、前回の続きで、UCBアルゴリズムについての紹介をします。問題設定は前回記事をご覧ください。

コイントスを少し考えてみる

この記事ではUCB(Upper Confidence Bound)アルゴリズムを紹介します。その紹介でどうしてもこれから紹介する考え方が必要なのでお付き合いください。

さて、今手元に表になる確率が0.7のコインがあるとします。このコインを数回投げて、実際に表になる割合を可視化してみましょう。

import random
def coin_toss(n_repeat, ratio=0.7):
  res = 0
  for _ in range(n_repeat):
    res += random.random() < ratio
  return res

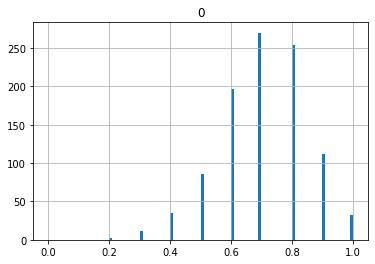
まずは10回投げたときの割合を1回の試行として1000試行したときにどうなるか見てみましょう。

import pandas as pd

results = []
n_repeat = 10
for _ in range(1000):
  
  results.append(coin_toss(n_repeat)/n_repeat)

df_ = pd.DataFrame(results)
df_.hist(range=[0,1], bins=100)

0.2から1.0まで広がっているのがわかると思います。
では、次に20, 50, 100, 200, 1000回投げたときの割合を1回の試行としてみましょう。

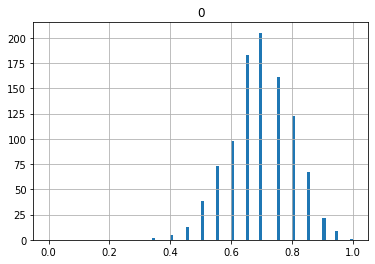
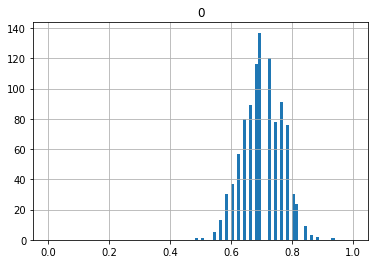
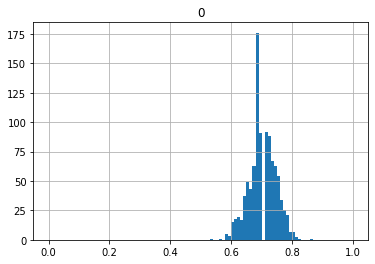
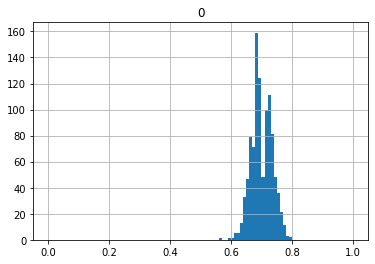
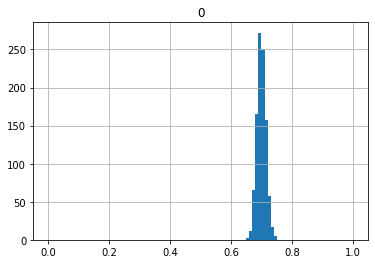
どんどん一つの点に収束していっているのがわかると思います。これを大数の法則といいます。
では逆に、1000回投げたときの割合が0.75だったときの真の値はいくつになるでしょうか？
上のグラフから考えるに1000回の時はおおよそ幅0.1に収まっているので、0.7から0.8になりそうだというのがわかると思います。
このように真の値がいそうな幅のことを信頼区間(confidence interval)といい、その上限や下限をconfidence boundといいます。
上の図から明らかなように信頼区間は回数を重ねるごとに小さくなりそうです。この性質をつかって真の値はどれだけ大きくなりうるのか？を評価するのがUCB(Upper Confidence Bound)法です。

UCB法

UCB法は基本的には信頼区間の上限を見てそれが大きそうなものを試すやり方です。それにいくらか工夫を重ねて実際はUCBスコアと呼ばれる

$$
\hat{\mu}_i(t) + \sqrt{\frac{\log t}{2 N_i(t)}}
$$

という量で判断します。ここで、$\hat{\mu}_i$はマシン$i$の結果から推定される確率。$t$は現在までに使ったコインの数。$N_i$は現在までにそのマシンに使ったコインの数です。

実験のコードを用意します。

import random
import math

class PlayBoard:
  def __init__(self, n_machines=3, n_coins=100):
    self.reset_machines(n_machines)
    self.reset_history(n_coins)

  def reset_machines(self, n_machines):
    self.n_machines = n_machines
    self.machine_mu =  [random.random() for _ in range(self.n_machines)]

  def set_machines(self, machine_mu):
    self.n_machines = len(machine_mu)
    self.machine_mu = machine_mu

  def reset_history(self, n_coins):
    self.n_coins = 100
    self.history = []
    self.reward = 0

  def play(self, arm):
    if self.n_coins < 1:
      return
    self.n_coins -= 1
    record = {'arm': arm, 'result': None}
    if random.random() < self.machine_mu[arm]:
      record['result'] = 1
      self.reward += 1
    else:
      record['result'] = 0
    self.history.append(record)
    return record['result']

class Score:
  def __init__(self, arm):
    self.arm = arm
    self.n_tries = 0
    self.reward = 0

  def get_ucb_score(self, count):
    if self.n_tries == 0:
      return 100_000_000
    return self.reward / self.n_tries + math.sqrt(math.log(count) / 2 / self.n_tries)

class Scores:
  def __init__(self, n_scores):
    self.scores = [Score(arm) for arm in range(n_scores)]

  def select_score_ucb(self, count):
    res_ = []
    for score in self.scores:
      res_.append({'arm': score.arm, 'score': score.get_ucb_score(count)})
    max_arm = max(res_, key=lambda x: x['score'])
    return self.scores[max_arm['arm']]

def ucb1(pb):
  scores = Scores(pb.n_machines)
  count = 0
  n_coins = pb.n_coins
  for score in scores.scores:
    res = pb.play(score.arm)
    score.n_tries += 1
    score.reward += res
    count += 1
  while count < n_coins:
    score = scores.select_score_ucb(count)
    res = pb.play(score.arm)
    score.n_tries += 1
    score.reward += res
    count += 1
  return pb.reward

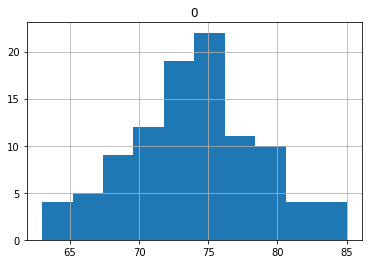
これで100回、前回と同様の条件で実験を行ってみます。

import pandas as pd

pb = PlayBoard()
pb.set_machines([0.3, 0.5, 0.8])


results = []
for _ in range(100):
  pb.reset_history(100)
  results.append(ucb1(pb))

df_ = pd.DataFrame(results)
df_.hist()

こちらは平均73.75と前回の70.9よりわずかに良くなっています。
どの条件下でどのアルゴリズムがよくなるかについては、次回DMED法を紹介した後に(もしくは独立した記事で)検討したいと思います。

おわりに

今回は多腕バンディット問題のなかでもUCB法について紹介しました。次回はより性能が得られるといわれるDMED法について紹介します。
さらに紙面があれば、今までのepsilon greedy, UCB, DMEDでどの条件下でどれが良いかについて考えてみたいと思います。次回も是非お付き合いください。