スロットマシンで稼ぐためには？（多腕バンディット問題入門）

　はじめに

こんにちは。株式会社エイアイ・フィールドでプロダクト開発をしている久保です。この記事はエイアイ・フィールドアドベントカレンダー2021の初日の記事です。この記事では、多腕バンディット問題と簡単なアルゴリズムの紹介をします。

　多腕バンディット問題とは

今、あなたはカジノに来ています。このカジノでは専用のコインを買い、そのコインをつかってスロットマシンで遊びます。スロットマシンからは当たれば現金が1万円出てくるものとします。（スロットマシンから出たコインではスロットマシンは起動できないものとします）。

さて、さっそくあなたはコインを100枚入手しました。

このコインをつかって、スロットマシンに挑みます。このカジノには3台のスロットマシンがあり、それぞれ当たる確率が異なることがわかっています。

さて、どのようにプレーをすれば最終的な獲得金額を最大化できるでしょうか？

このように、選択肢の候補から1つを選び、選んだ選択肢からは確率に従って報酬が得られ、それ以外の選択肢からは情報も得られない。それをN回繰り返すときに報酬を最大化する問題を多腕バンディット問題とよびます。

素朴な方法

獲得金額を最大化するためのもっともよいやり方は、3つのスロットマシンの中で最も当たる確率の高いものにすべてのコインを使うことです。しかし、最初の段階では、どのスロットマシンが最も当たる確率が高いのかは分かりません。なので、ある程度調査(探索)が必要になります。
例えば、100枚のうち、最初の30枚を調査に使い。その中で最も有望そうなマシンに残りの70枚を使って(知識利用して)みましょう。

以下に多少汚いですが、sample codeを置きます。

import random

class PlayBoard:
  def __init__(self, n_machines=3, n_coins=100):
    self.reset_machines(n_machines)
    self.reset_history(n_coins)

  def reset_machines(self, n_machines):
    self.n_machines = n_machines
    self.machine_mu =  [random.random() for _ in range(self.n_machines)]

  def set_machines(self, machine_mu):
    self.n_machines = len(machine_mu)
    self.machine_mu = machine_mu

  def reset_history(self, n_coins):
    self.n_coins = 100
    self.history = []
    self.reward = 0

  def play(self, arm):
    if self.n_coins < 1:
      return
    self.n_coins -= 1
    record = {'arm': arm, 'result': None}
    if random.random() < self.machine_mu[arm]:
      record['result'] = 1
      self.reward += 1
    else:
      record['result'] = 0
    self.history.append(record)

  def get_summary(self):
    ret = [{'arm': idx, 'n_choice': 0, 'n_reward': 0} for idx in range(self.n_machines)]
    for r in self.history:
      ret[r['arm']]['n_choice'] += 1
      ret[r['arm']]['n_reward'] += r['result']
    for r_ in ret:
      r_['est'] = r_['n_reward'] / r_['n_choice'] if r_['n_choice'] else 0
    return ret

def epsilon_greedy(pb, eps = 0.3):
  n_exploration = int(eps * pb.n_coins)
  n_exploitation = pb.n_coins - n_exploration
  for idx in range(n_exploration):
    pb.play(idx % pb.n_machines)
  max_arm = max(pb.get_summary(), key=lambda x: x['est'])['arm']
  for _ in range(n_exploitation):
    pb.play(max_arm)
  return pb.reward

PlayBoard は状況設定を表すクラスで、reset_machines, set_machinesはスロットマシンをresetのほうはランダムで、setのほうは任意で用意できます。reset_historyでは履歴とコインのリセットを、playではマシンを選んで遊ぶことを行います。最後のget_summaryは現在までにどのマシンをどれだけ選んだか、そのマシンから報酬を得られたのは何回か、報酬を得られる経験的な割合はいくらかをまとめて出します。

epsilon_greedyは先ほど紹介した素朴なアルゴリズムで、全体のうちeps分だけ探索をして、最も有望そうなマシンに残り全部を使います。

これらのコードを用いて、何回も実験を行い。最終的にどのように報酬が得られるか見てみることにしましょう。

pb = PlayBoard()
pb.set_machines([0.3, 0.5, 0.8])

今回は、マシンとして確率0.3, 0.5, 0.8で報酬を返すものを用意しました。なので、最も良いマシンを選び続けたときの報酬の期待値は80万円となります。

results = []
for _ in range(100):
  pb.reset_history(100)
  results.append(epsilon_greedy(pb))

このようなコードで100回ほど実験をしてみました。

import pandas as pd
df_ = pd.DataFrame(results)
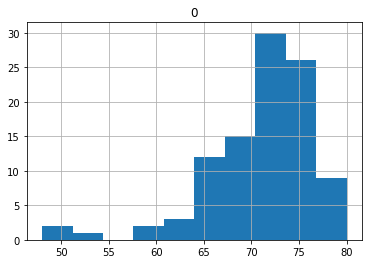
df_.hist()

結果

となり、平均70.9の報酬がもらえました。まだ、50のところに山がありそうで、0.5の報酬に引っ張られたように見受けられます。
探索が足りなかったかもしれないので、epsを0.4まで上げてみましょう。

results = []
for _ in range(100):
  pb.reset_history(100)
  results.append(epsilon_greedy(pb, 0.4))

df_ = pd.DataFrame(results)
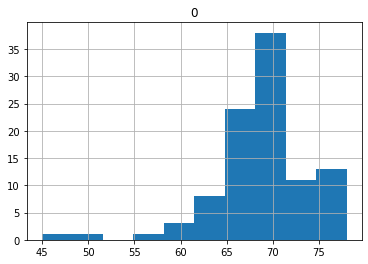
df_.hist()

結果、このようになりました。50へ引っ張られているものは減りましたが、探索を増やした分期待報酬も減ってしまい。平均では68.81となっています。

ほかの方法

このバンディット問題ですが、上に紹介した素朴なアルゴリズムはepsilon greedy法と呼ばれています。ほかのアルゴリズムも考案されており、UCB法やUBT法、また問題を強化学習と考えQ-Learningで解く方法などがあります。この記事が長くなってしまったので、これらについては次回以降の記事でできれば紹介したいと思います。

おわりに

今回は多腕バンディット問題の紹介とその中でも最も素朴なアルゴリズムであるepsilon greedy法について紹介しました。多腕バンディット問題はこのようなスロットマシンの問題だけでなく、もう少し問題を拡張することによって広告配信や推薦、囲碁などのゲーム木探索などにも応用されているます。また、問題の形式を少し変えることによって、デザインにおけるA/Bテストの世界ともつながっていきます。
興味がわいた方は、本多さんの本などを読んでみるとよいかもしれません。もちろん次回以降にも他のアルゴリズムや拡張問題について書いていくつもりですので、ぜひご期待ください。