ノンパラメトリックベイズは無限次元のベイズモデルと言われます。
前回の記事でやったガウス過程もノンパラメトリックベイズですが、もうひとつ有名なものはディリクレ過程です。
理論的な説明は、「ノンパラメトリックベイズ(機械学習プロフェッショナルシリーズ)」やこちらのQiita記事が参考になります。
そもそもベイズ推論は以下の3ステップで行います。
- パラメータの事前分布と事象の確率モデルを定義する
- 得られたデータと確率モデルから尤度を計算し、パラメータの事前分布と掛けることでパラメータ事後分布を計算する(ベイズの定理)
- パラメータ事後分布と確率モデルからデータの予測確率分布を生成する
この2つ目のステップの際に事前分布と事後分布が同じ分布になるものを共役事前分布と言います、
ベータ分布はニ項分布モデルの共役事前分布であるように、ディリクレ分布は多項分布モデルの共役事前分布になります。
つまり、ディリクレ分布はベータ分布を多変量にした分布になります。
無限次元でのディリクレ分布を考えたものがディリクレ過程になります。
ガウス過程が無限次元の多変量ガウス分布であるのと同じような感じです。
ただしガウス過程は無限区間ですが、ディリクレ過程は0から1の有限区間です。
そのため、ディリクレ過程はクラスタ割合の確率モデルとなるイメージです。
これによって、クラスタ数を自動的に決定するクラスタリング(ディリクレ過程混合モデル(DPMM))が可能になります。
ただし、ディリクレ過程は無限個の要素があるため実装することが難しいです。
そこで方法としては2つです。
①無限ではなく有限次元で近似する方法。打切り棒折り過程(TSB)や有限対称ディリクレ分布(FSD)を用います。変分ベイズで解くことが可能です。
②無限個の要素を積分消去した中華料理店過程 (CRP)、ピットマン・ヨー過程を用いる方法。この方法では変分ベイズをすることができず、MCMCしかできません。
今回はPyroで①による実装を行います。
*Tensorflow Probabilityによる実装ではこちらの記事が参考になります。
参考文献
Bingham, E., Chen, J. P., Jankowiak, M., Obermeyer, F., Pradhan, N., Karaletsos, T. et al. (2019).
Pyro: Deep universal probabilistic programming. The Journal of Machine Learning Research, 20(1), 973-978.
コードは以下にあるものを改変して使用しています。
https://github.com/pyro-ppl/pyro (Apache-2.0 License)
Pyroでディリクレ過程混合モデル(TSB)
例えばk-means法やガウス混合モデルでのクラスタリングでは、クラスタ数をパラメータとして指定する必要があります。(この場合はAICなどを計算して最適なものを決定する。)
それに対して、このディリクレ過程混合モデルでのクラスタリングでは自動的にクラスタ数が決定できるため、柔軟なクラスタリングが可能とされています。
Pyroでは、ディリクレ過程はガウス過程のように専用のclassはないのでモデルから実装することになります。
今回は公式チュートリアルの例を参考にTSB(打切り棒折り過程)を実装します。
import torch
import pyro
import pyro.distributions as dist
import matplotlib.pyplot as plt
pyro.set_rng_seed(101)
まずはデータを作成します。
4つの二次元ガウス分布から200個ずつのデータをサンプリングします。
num = 200
data = torch.cat((dist.MultivariateNormal(-8 * torch.ones(2), torch.eye(2)).sample([num]),
dist.MultivariateNormal(8 * torch.ones(2), torch.eye(2)).sample([num]),
dist.MultivariateNormal(torch.tensor([-5., 5.]), torch.eye(2)).sample([num]),
dist.MultivariateNormal(torch.tensor([6., -5.]), torch.eye(2)).sample([num])
))
plt.scatter(data[:, 0], data[:, 1])
plt.show()
この800個のデータをクラスタ数(この場合では4)を指定せずにクラスタリングします。
棒折りをする関数を定義します。
import torch.nn.functional as F
def mix_weights(beta):
beta1m_cumprod = (1 - beta).cumprod(-1)
return F.pad(beta, (0, 1), value=1) * F.pad(beta1m_cumprod, (1, 0), value=1)
TSBの確率モデルを定義します。
alphaは集中度パラメータで、クラスタ割合のばらつき度合いを表します。
Tはクラスタ数の上限です。今回は10に設定しました。
N = data.shape[0]
T = 10
alpha = 0.1
def model(data):
with pyro.plate("beta_plate", T-1):
beta = pyro.sample("beta", dist.Beta(1, alpha))
with pyro.plate("mu_plate", T):
mu = pyro.sample("mu", dist.MultivariateNormal(torch.zeros(2), 5 * torch.eye(2)))
with pyro.plate("data", N):
z = pyro.sample("z", dist.Categorical(mix_weights(beta)))
pyro.sample("obs", dist.MultivariateNormal(mu[z], torch.eye(2)), obs=data)
autoguideは使えないので、自分でguide関数を定義します。
from torch.distributions import constraints
def guide(data):
kappa = pyro.param('kappa', lambda: dist.Uniform(0, 2).sample([T-1]), constraint=constraints.positive)
tau = pyro.param('tau', lambda: dist.MultivariateNormal(torch.zeros(2), 3 * torch.eye(2)).sample([T]))
phi = pyro.param('phi', lambda: dist.Dirichlet(1/T * torch.ones(T)).sample([N]), constraint=constraints.simplex)
with pyro.plate("beta_plate", T-1):
q_beta = pyro.sample("beta", dist.Beta(torch.ones(T-1), kappa))
with pyro.plate("mu_plate", T):
q_mu = pyro.sample("mu", dist.MultivariateNormal(tau, torch.eye(2)))
with pyro.plate("data", N):
z = pyro.sample("z", dist.Categorical(phi))
変分ベイズを実行します。
from pyro.optim import Adam
from pyro.infer import SVI, Trace_ELBO
from tqdm import tqdm
optim = Adam({"lr": 0.05})
svi = SVI(model, guide, optim, loss=Trace_ELBO())
losses = []
num_step = 1000
pyro.clear_param_store()
for j in tqdm(range(num_step)):
loss = svi.step(data)
losses.append(loss)
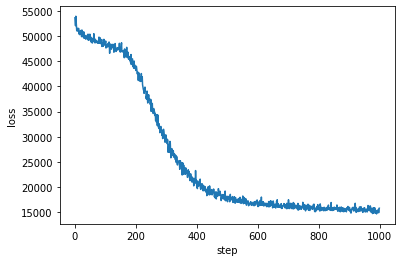
plt.plot(losses)
plt.xlabel("step")
plt.ylabel("loss")
事後確率の少ないクラスを消去する(打切りをする)関数を定義します。
def truncate(alpha, centers, weights):
threshold = alpha**-1 / 100.
print(threshold)
true_centers = centers[weights > threshold]
true_weights = weights[weights > threshold] / torch.sum(weights[weights > threshold])
return true_centers, true_weights
事後確率の少ないクラスを消去して、予測結果を表示します。
Bayes_Centers, Bayes_Weights = truncate(alpha, pyro.param("tau").detach(), torch.mean(pyro.param("phi").detach(), dim=0))
plt.scatter(data[:, 0], data[:, 1], color="blue")
plt.scatter(Bayes_Centers[:, 0], Bayes_Centers[:, 1], color="red")

4つのクラスが認識されました。中心もかなり正確に捉えていると思います。
これはうまくいった例ですが、alphaやTの値によってはうまく行かなかったです。
他の応用
構造変化推定
時系列データに対して線形回帰モデルを当てはめるときに、ディリクレ過程によって無限の線形モデルを考えます。
モデルごとにクラスタリングをすることで、時系列データの分節化を行うことが出来ます。
参考:https://www.slideshare.net/shotarosano5/in-62843951
HDP-LDA
LDA(潜在的ディリクレ配分法)は教師なし学習で、トピックモデルに使われます。(LDAのPyro実装例)
HDP(階層ディリクレ過程)を使用したHDP-LDAは適切なトピック数が自動が決定できます。
GensimというPythonライブラリで簡単に行えるようです。
階層ディリクレ過程はCRP(中華料理店過程)を1段階複雑にした、CRF(中華料理店フランチャイズ)がモデルになります。
終わり
ノンパラメトリックベイズはパラメータが無いのではなく、無限または多数のパラメータを考えている(パラメータ数の制約が無い)ということだと思いました。
しかし、今回のTSBの実装ではクラスタ数の上限を設定しなければならないので注意です。
上限を設定しなくて良いCRPの実装もやってみたいですね。