ノンパラメトリックベイズ入門
ノンパラメトリックベイズのことを最近勉強したので頭の整理もかねてまとめてみました。
特に専門でもないので間違いがあったら指摘していただけると助かります。
モチベーション
ノンパラメトリックベイズは簡単に言えば無限次元のベイズモデルです。(パラメータがない訳ではないです)理論自身はかなり前からもう既に大体出来ていて2000年代になってから機械学習の文脈でそれが使えるってなってきたらしいです。
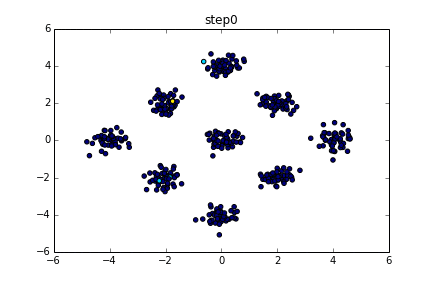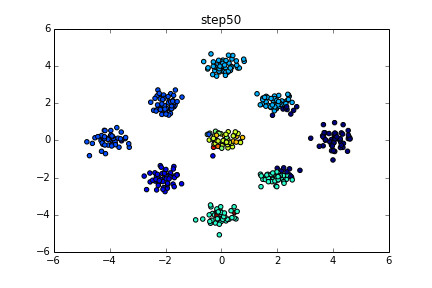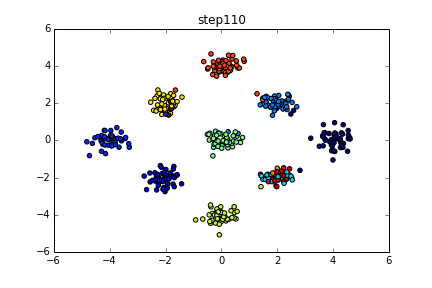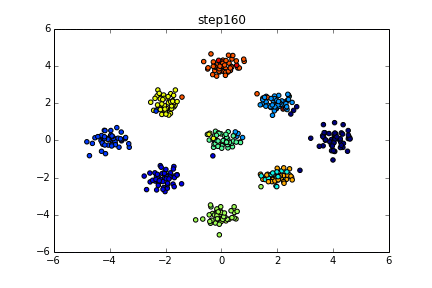
例えばクラスタリングをするとき普通、混合数を指定します。しかしノンパラメトリックベイズでは一旦、無限個のクラスターがあると考えることで自動的に混合数が決まります。
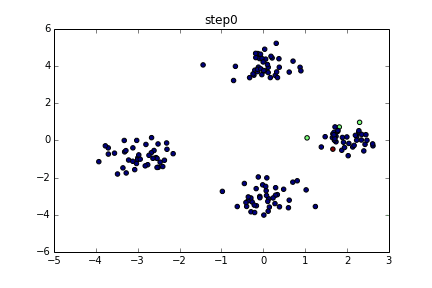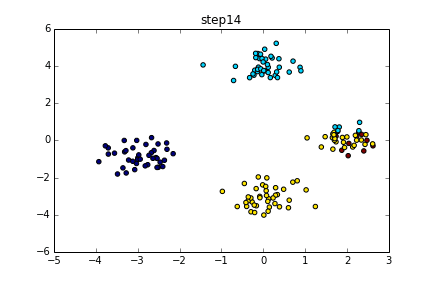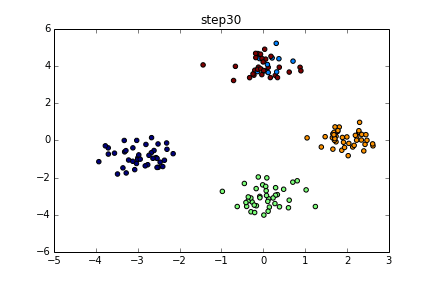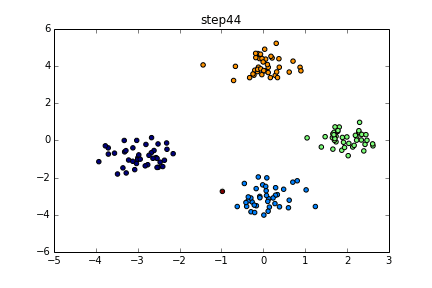
具体的にいうと下のようなgifのようになります。
色が同じだと同じクラスターとしています。クラスター数を指定している訳ではないですが上手くクラスタリングできていることが分かると思います。今回はこの無限混合モデルの実装を目標とします。
コードは
https://github.com/Ma-sa-ue/practice/tree/master/machine%20learning(python)/nonparabayes
にあげてあります。ノンパラベイズのクラスタリング以外での機械学習での応用例としては
- 回帰(カーネル回帰はGaussian processを使っている。関数にpriorを敷いてると言えノンパラメトリックベイズの一種と言える。)
- 隠れマルコフモデル(潜在数などを固定しない。)
- 推薦モデル(Collaborative filtering)
- 密度推定
があります。またメリットとしては(重なっていますが)以下のようなことがあります。
- 表現できる関数が豊富になる
- OverfitもせずUnderfitもしない
- 従来的な意味でのモデル選択をしなくてよい
簡単な概要
さきほど言ったよう無限混合モデルの実装を目標とします。
そのためにまずノンパラベイズにおける部品となるDirichlet process, Stick breaking process, Chinese restaurant processについて説明します。3者は別々のものではなく、見方の違いでもあるということが重要です。
その後、混合分布モデルの文脈で上を再整理します。そして無限混合モデルの実装を行います。
またその後で理論的な背景について整理しました。
偉そうなこと言える立場では全然ありませんが、自分が勉強したときは一つの文献では全然よく分からなかったので、色んな文献を参照したり実装してみることをオススメします。
基本編
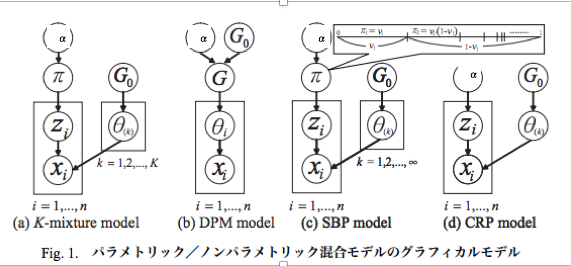
これは上田先生のチュートリアル(文献1)から引用させて頂いた図です。この図を理解すること一つの目標と言えます。
有限混合モデル
まず無限の前に有限混合モデルがどうなるかについて書きます。
(a)のようなgraphical modelで表すことができます。具体的には
$\theta_{k}\sim G_{0}$, $\pi =(\pi_{1},...,\pi_{K}) \sim Dirichlet(\frac{\alpha}{K},...,\frac{\alpha }{K})$
$z_{i}|\pi \sim Multinomial(\pi)$
$x_{i}|z_{i},\theta_{k} \sim f(\theta_{z_{i}})$
となります。$x=(x_{1},...,x_{n})$が観測値で$z=(z_{1},...,z_{n})$がラベルとなります。
$\pi $がラベルを決めるためのサイコロです。
混合Gauss分布の場合、fはGauss分布で$\theta =(\theta_{1},...,\theta_{k})$ はK個あるそれぞれのクラスの平均になります。$G_{0}$はパラメータのpriorです。混合Gauss分布の場合で共役にとるとこちらもGauss分布になります。
観測できるのは$x$だけですが、本当は真の$z$(ラベル)を知りたいとします。有限混合モデルの場合、基本的には$z$と$\theta$に関してGibbs samplingすることで求めることができます。また$K$を無限に持って行くことで無限混合モデルにおいての手法を作ることができます。しかしこれをいざ"そのまま"実装するとなると無限個のクラスがあって無理なことが分かります。
Dirichlet分布
Beta分布の多変数バージョンがDirichlet分布です。Dirichlet分布はベイズだと多項分布のpriorとしてよく出てきます。このときK次元のDirichlet分布から生成されたサンプルは和が1となることが重要です。
ここでは$G =\sum _{k=1}^{K} \pi _{k} \delta _{\theta _{k}}$について考えます。
($\pi \sim Dirichlet(\alpha/K,...,\alpha /K),\theta \sim H$に注意)
そうすると混合モデルにおいて$p(x)=\int p(x|\theta)G(\theta )d\theta$となることが分かります。(zが消去されます)
すると有限混合モデルのgraphical modelの形は(b)みたいになります。
このときKの個数が無限となった場合のGからサンプリングしてきたいというモチベーションでDirichlet processを使うことになります。
Dirichlet Process
もともとのDirichlet processの導入は理論編の所に書いてあります。Dirichlet processは$DP(\alpha ,H)$と表示します。
先ほど言った通りDirichlet processはほとんど至る所離散で$G =\sum _{k}^{\infty} \pi _{k} \delta _{\theta _{k}}$(無限和)となります。Dirichlet processからサンプリングしてくるためにはStick-Breaking processを使います。
Stick-Breaking Process
Dirichlet processからサンプリングするためには
$\theta_{k} \sim H$,$v_{k} \sim Beta(1,\alpha )$,$\pi_{k}=v_{k}\prod_{j=1}^{k-1} (1-v_{j})$,$G=\sum _{k=1}^{\infty} \pi _{k} \delta _{\theta _{k}}$
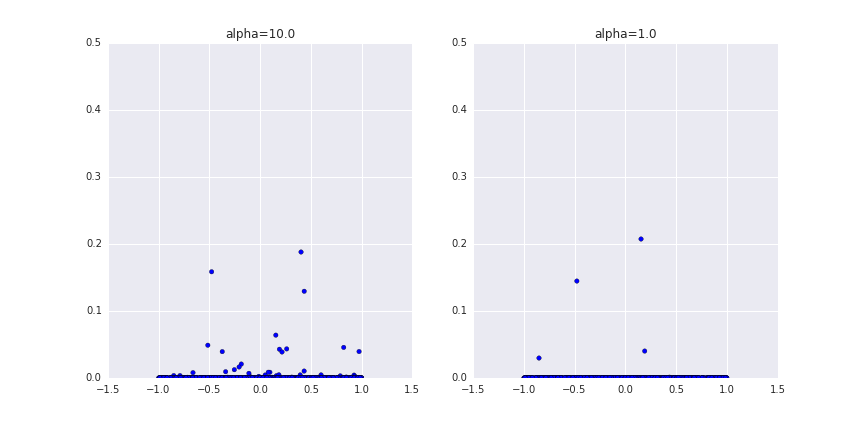
としてサンプリングします。$\pi _{k}$の和が1になるように整合性が取れています。だんだん枝を折っていく感じだからStick-Breaking Processと言われていると思われます。サンプリング例を下に記します。
もちろん無限個の和となったGは本来は作れないので近似的なものです。$\alpha $が大きいほど枝がたくさんできることが分かると想います。
あと実際の実装で使う重要なことして以下のような性質があります。
$\theta_{i}|\theta_{-i} \sim \frac{1}{i-1+\alpha}\sum_{j=1}^{i-1} \delta (\theta_{j}) + \frac{\alpha }{i-1+\alpha }G_{0}$
Chinese Restaurant Process(CRP)
CRPとはクラスターのインデックスのpartionの分布です。
とりあえず天下り的な導入をまずします。
例えば全体集合を$[n]=[1,2,...n]$と表記しpartionの元を$\rho $と書くようにします。
$\rho $の例としては全体集合が[4]のとき[[1],[2,3],[4]]とか[[1,2],[3,4]]が考えられます。partionの以下のような作り方がCRPとなります。
まず中華料理店に次々に一人一人入っていきテーブルに座っていくことを想像します。
n人が座っている時のn+1人目の座り方が
P(既にあるテーブルcに座る確率)=$\frac{n_{c}}{a+n}$,P(新しいテーブルに座る確率)= $\frac{\alpha}{\alpha + n}$
となるとして、これを続けていったときの最終的なpartionの分布がCRPとなります。($\alpha$は定数、$n_{c}$はcに既に座っている人の数です)
例えば既に4人が入っていて一人、三人と座っていると[[1],[2,3,4]]というようになります。
そこで5人目の入り方を考えます。
すると$\alpha =1$とすると1番目のテーブルに座りる確率は$\frac{1}{1+4}$,2番目のテーブルに座る確率は$\frac{3}{1+4}$,3番目(新しい)テーブルに座る確率は$\frac{1}{1+4}$となります。
既にたくさんの人が座っているテーブルはさらに人が集まるという性質に注意してください。
partionを作るということはまさにクラスタリング(ラベルづけ)と同じ行為であることにも注意してください。
例えば上の例で人をテーブル番号でラベル付けしてみます。5人目が新しいテーブルに座るとすると[2,1,1,1]の状態から[2,1,1,1,3]に移るということです。
また$\alpha $が大きくなるにつれ客がまばらに座るという性質にも注意してください。
実際に実装してみます。基本的には上をそのまま実装してみればいいのですがあっているかよく分からないかもしれません。その時はテーブルの個数と客の人数に対する関係が成り立つことを見れば大体確認できます。
その関係は
$E[|\rho |] \approx \alpha \log(1+\frac{n}{\alpha})$
となっていて実際にグラフを書いてみるとしたのようになります。
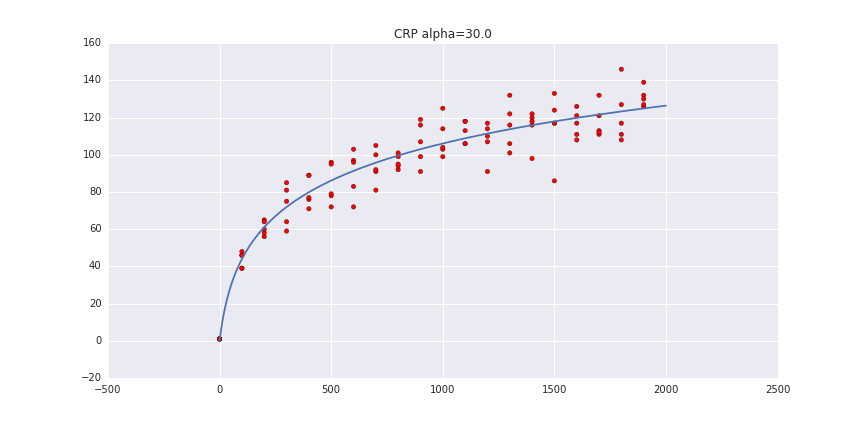
x軸は客の人数でy軸はテーブルの個数です。赤い点はサンプリンングしてきた点で青い線が期待値の近似値です。大体それっぽくなっていることが分かると思います。
混合モデル再考
今までことを考慮して再度以下の図を整理してみます。
(a)は先ほど言った通りです。学習方針としては$z$,$\theta $のGibbs samplingがあります。
(b)も基本的には先ほど言った通りです。Dirichlet processを直接扱うのは難しいので実質的には(c)となります。この場合はラベル(z)は明示的に求めず$\theta $を求めることになります。これは$\theta $に関するGibbs samlingによって求めます。このときGからのサンプリングを行う必要がありますが厳密な意味ではできないことに注意してください。この場合、$\theta$と$\pi$を無限個用意する必要があるからです。
しかしよく考えてみればデータ点におけるクラスターだけに注目すればいいと分かります。これが(d)となります。そのためにまず有限混合モデル(a)におけるzの事後分布について考えてみます。すると簡単な計算($\pi$を積分消去)により
$P(z_{i}=c|z_ {-i},\alpha ,K)=\frac{n_{c}+\alpha /K}{n-1 + \alpha }$ ($n_c$はcにクラスタリングされているzの個数、Kはクラスター数、$z_{-i}$は$z_{i}$以外のz)
となります。$K \to \infty$とすることによって分子が$n_{c}$となり$z_{i}$が客、クラスがテーブルとすることによってまさにCRPとなることが分かります。
式で書くと(d)は下のようになります。
$z |\alpha \sim CRP([n],\alpha )$,$\theta _{c}|H \sim H(c\in \rho)$
$x_{i}|\theta _{c} \sim F(\theta _{c})$
(CRPはpartionの分布といいましたが[n]に対してpartionを作るということは$z_{i}$にラベル付けすることと同じなことに注意してください。CRPからpartion:$\rho $が生成されてそれに基づいてラベルづけたのがzとなるという意味で解釈してください)
実装編
いよいよ実装パートに移ります。基本的にはMCMCを使います。方針としては先ほどのgraphical modelに基づいて忠実にMCMCしていく感じです。Nealの論文(参考文献5)に基づいて実装しています。今までのことや実装法も分かりやく書いてあるのでぜひ読むことをお勧めします。
CRPによる実装
まず図の(d)に基づいた実装を行います。$z$と$\theta $に対して1次元ずづ順番に遷移させていくという手法を使います。
まず単純に思いつくのが下の式を利用してGibbs samplingすることです。
$P(z_{i}|z_{-i},x_{i},\theta )\sim P(z_{i}|z_{-i})P(x_{i}|z_{i},\theta )$
If $c=z_{j}$ for some $j\neq i$ then $P(z_{i}=c|z_{-i})= \frac{n_{-i,c}}{n+1+\alpha}$, $P(x_{i}|z_{i},\theta ) = f(x_{i}|\theta_{z_{i}})$
If $c=z_{i}$ is new then $P(z_{i}|z_{-i}) = \frac{\alpha }{n+1+\alpha}$, $P(x_{i}|z_{i},\theta ) = \int f(x_{i},\theta )dG_{0}(\theta)$
一番上の式をそのまま利用して$z$をgibbs samplingしていくことはあまり良くないです。なぜなら遷移確率を計算するときに積分計算が出てくるからです。しかも正規化されていないので正規化項を計算する必要があります。
そこでそもそもGibbs samplningは採択率が1となっているMetropolis-Hastings alogrithmであったことを思い出してみます。
と同時に$P(z_{i}|z_{-i})$の計算が簡単であることをみてみます。
すると遷移確率を$P(z_{i}|z_{-i})$とすることによってMetropolis-Hastingsすれば遷移するための計算の手間が簡単になることに気づきます。採択率を計算するときに積分が残ってしまうという説がありますがそれは一回のサンプリングで回避します。
つまり採択率は$\alpha (z_ {i}^{*},z_ {i})$ は
$min[1,\frac{f(y_{i},\theta_{z_{i}}^{*})}{f(y_{i},\theta_{z_{i}})}]$
となります。アルゴリズムを整理すると以下のようになります。
- repeat the following procedure many times
- for i=1,...n repeat the following update of $z_{i}$ R times:
- draw a candidate $z_{i}^{*}$ from $P(z_{i}|z_{-i})$
- if $z_{i}^{*}$ is not a new value, calucate the acceptance rate.
- if $z_{i}^{*}$ is a new value, draw $\theta$ from $G_{0}$ then calucate the acceptance rate
- update $z_{i}$ according to the acceptance rate
- for all $\theta$, draw a new value from posterior distibution
- for i=1,...n repeat the following update of $z_{i}$ R times:
K-meansっぽくなっていることが分かると思います。$\theta$の更新は事後分布からすると書いてありますが今回はpriorにgauss分布を使ったので事後分布もgauss分布となっています。
またRは3回以上が推奨されます。R=1だと新しいクラスターにあまり人が集まらない場合があるからです。
実際に実装してみると以下のようになります。
$\alpha$はクラスター数が出来過ぎないように大きくない値が推奨されます。(1ぐらいとか?)最初のgifではきちんと4つに分かれていましたが今回はさらに複雑にしています。
SBPによる実装(explicit-G-sampler)
次に図の(b)と(c)に基づいた実装を行います。
具体的なモチベーションは$\theta $の事後分布から以下の式を使ってサンプリングすることになります。
$\theta_{i}|\theta_{-i} \sim \frac{1}{n-1+\alpha }\sum_{j=1}^{n-1} \delta (\theta_{j}) + \frac{\alpha }{n-1+\alpha }G_{0}$
もちろんGのサンプリングはできないため擬似的なサンプリングになります。
$\theta_{i}$の添え字の意味がクラスターからサンプルに対してになっていることに注意してください。
今回もCBPのときの実装みたいにただそのままGibbs samplingをするのではなく遷移確率を$\theta_{i}|\theta_{-i} $とします。採択率は$\alpha (\theta_{i}^{*},\theta_{i})$ は
$min[1,\frac{f(y_{i},\theta_{*})}{f(y_{i},\theta_{i})}]$
となります。整理すると$\theta_{i}(i=1,...n)$を上の採択率で順番にサンプリングしていけばいいと分かります。すると下のようになります。
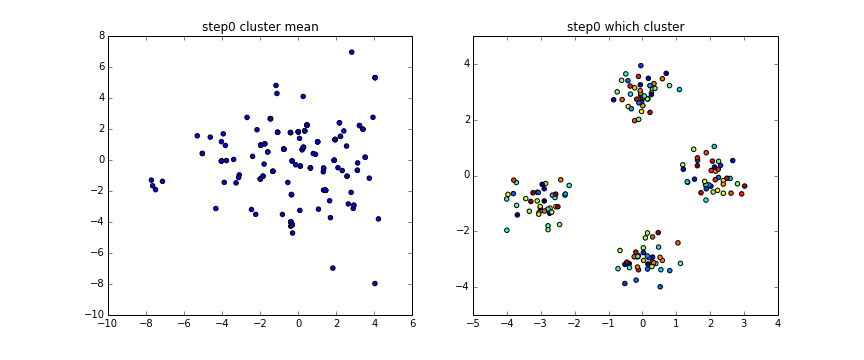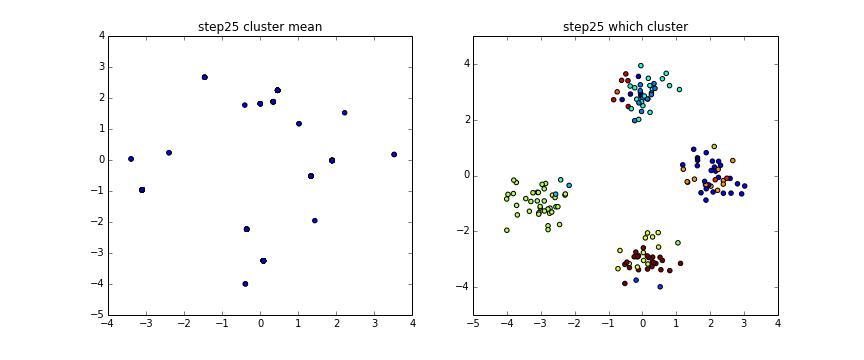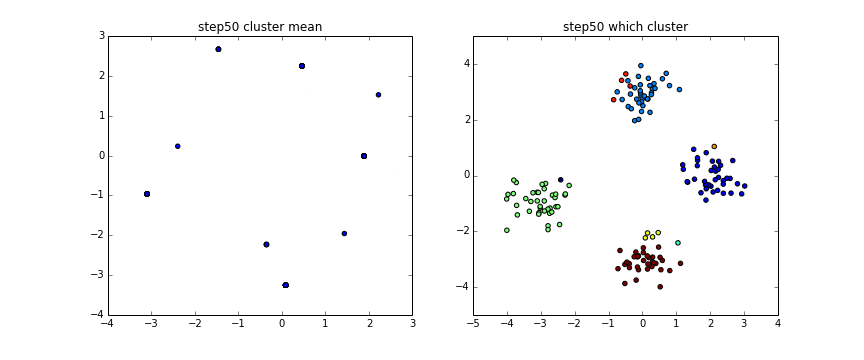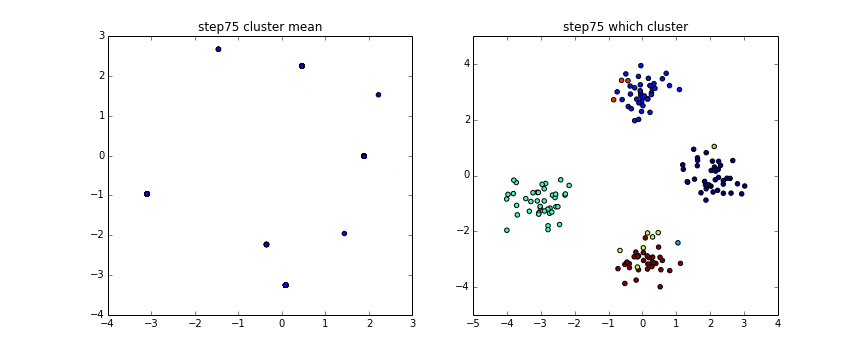
上のgifでは$\alpha =1$としています。
左が$\theta$、右がそれから得られるクラスターによって色分けしたものです。
完全に4つには分かれてはいませんがもっとstep数増やすともう少しうまく別れます。
理論編
"機械学習系"の人にとって理論的なことを書きます。"統計学系"の人にとって理論的なことを知りたければ加藤先生のtutorial(参考文献9)とかを読むといいと思います。(自分は読んでいないです)
De Finetti's Theorem
ベイズ流を正当化するDe Fineti's theoremについてまず書きます。
上で扱ったCRPとかは観測が交換可能でした。つまり$X_{1}, X_{2},...,X_{n},...$という確率変数があったときにインデックスを置換しても同時確率は変わりませんでした。数式でいうと
$P(X_{1}=x_{1},X_{2} = x_{2},...)$=$P(X_{1}=x_{\sigma (1)},X_{2}=x_{\sigma_{2}},...)$
となります。ちなみに交換可能という条件はi.i.dという条件より弱いです。
De Finetti's Theoremは交換可能な$X_{1},X_{2},...$という確率変数があるとき以下を満たす$\theta $が
$P(X_{1},...,X_{n}) = \int P(\theta )\prod_{i=1}^{n}P(X_{i}|\theta )d\theta$
存在することを主張します。この定理によってベイズ流が正当化されます。上の無限混合モデルでは$P(\theta)$はrandomなpdf($G=\sum \pi_{k}\delta _{\theta _{k}})$となっていました。
そもそものDirichlet processの定義
Dirichlet proceessは確率空間があって(randomな)測度をGとするとき任意の分割$A_{1},...,A_{n}$に対して$(G(A_{1}),...,G(A_{n}))$が$(\alpha H(A_{1}),...,\alpha H(A_{n}))$をパラメータとするようなDirichlet分布に基づいているときの$G$というのが定義です。
これだとよくイメージが掴めないですがGはほとんど至る所離散でSBPでやったように表示できることが知られています。
連続時間の確率過程の表現1
一般的に確率変数$X$($X$は$\Omega$から$\mathbb{R}$への可測関数) が与えられたら普通は引き戻し測度みたいなのを$\mathbb{R}$のボレル空間上に定義してその後、Radon–Nikodymによりpdfを考えたりします。
そのような確率変数の集合が確率過程{$X_{t}$}($t\in T$)です。
最も簡単なi.i.dな確率過程が有限個ある場合は直積空間に直積測度を考えることによって存在が保証されます。Tが無限集合であったりi.i.dでない場合そのような確率過程の存在を言いたかったらKolmogorovの拡張定理を使います。
Kolmogoroveの拡張定理とはTが可算集合の場合、任意のTの有限部分集合のいかなる同時分布にも整合性が存在するならそのような確率過程が存在するという定理です。
例えばBrownian motionであったりPoisson processの場合は$T=\mathbb{R}$ですが一旦、$\mathbb{Q}$に拡張定理を使って$\mathbb{Q}$は$\mathbb{R}$の中で稠密という性質を使って連続的に定義してあげます。
しかしDirichlet processの場合この$T$がまさかの$\mathbb{R}$のボレル集合な訳です。可算では勿論ないのでボレル集合の中で可算となるような集合をとってきてさらに連続的に伸ばして構成するらしいです。もはや連続時間というイメージからはかけ離れてしまいます。
連続時間の確率過程の表現2
上の構成からだとDirichlet processは訳わかんない感じになっていますが幸いなことにSBPとして表せることが知られていてそれを使ってサンプリングすることができます。上の実装でもその表現を使いました。
その他
雑多に上に書いていないことで重要そうなことを書いています。
Pitman-Yor Process
せっかくCRPをやったのでPitman-Yor Processについても触れておきます。PYPはCRPを少し変えてやったやつです。
式としてはCRPと同じシチュエーションで下のようになります。
P(既にあるテーブルcに座る確率)=$\frac{n_{c}-d}{a+\sum_{c\in \rho} n_{c}}$,P(新しいテーブルに座る確率)= $\frac{\alpha +d|\rho|}{\alpha + \sum_{c\in \rho} n_{c}}$
またd=0.9(緑)、d=0.5(青)、d=0.1(黄)としてグラフ(log10 scale)を描くと下のようになります。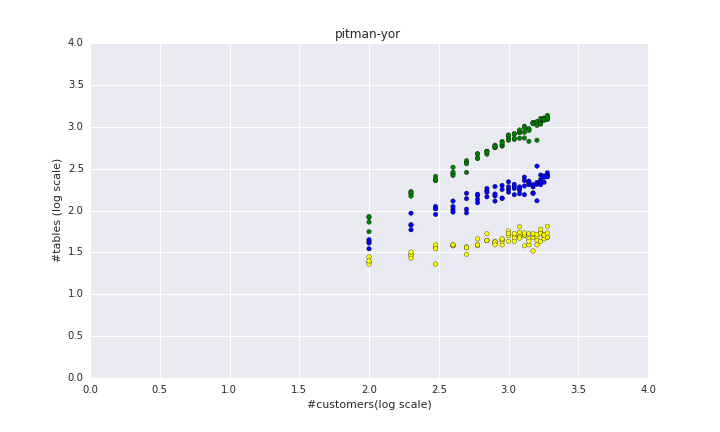
上を見ると$d$を増やすごとにテーブル数が増えていくことが分かります。
$d$はテーブルあたりの人数を減らしているというのもありますが同時にテーブル数とテーブルあたりの客の数がべき乗則に従うように調節しています。(ネットワークの本とかを読んだ人知っているかもしれませんが世の中のクラスター数とクラスターあたりの人はべき乗則に従うという経験的な法則があります)
Pitman-yor processは現実データに即しているということで自然言語処理とか画像処理とかでも使われます。
ノンパラベイズはどういうときに使えるのか?
理論的なとこでも触れたようDirichclet processでは観測が交換可能で同質(同じ基底分布からきている)になっています。例えば無限混合モデルのgibbs samplingにおいてもこの同質性を暗に使っています。
しかし残念ながら世の中の現象は全てそんな同質な基底分布ばかりから来ている訳ではないです。
そこでさらにDirichlet processからサンプルしてそれを基底分布としてさらにDirichclet processを生成するHierarchil Dirichlet processを使ったりします。
MCMC以外の手法は?
勿論、変分ベイズでもできるらしいです。しかしMCMCの方が(アルゴリズムを作るのが)簡単です。
触れていないけど重要そうな話題
今回触れていないけど重要そうなことをkeywordであげてみました。
Infinite HMM, Indian buffet process,Polya Trees,Hierarchical Dirichlet Processes.
また自分も勉強中なので実際に実装してみたらまた記事にしてみるかもしれません。
参考文献
- NTTの上田先生の作ったtutorial とても分かりやすくまとまっている。この記事もかなり影響を受けている。IRMとかについて詳しく載っている。続パタにも勿論載っています。
http://www.kecl.ntt.co.jp/as/members/yamada/dpm_ueda_yamada2007.pdf - 京大の吉井先生の作ったスライド とても分かりやすい。
http://sap.ist.i.kyoto-u.ac.jp/members/yoshii/slides/mus91-tutorial-npb.pdf - OxfordのYee Whye Tehのホームページ 参考になるtutorialがたくさん載っている。http://www.stats.ox.ac.uk/~teh/npbayes.html
- ↑の先生の自分の聞いた講義 最初聞いたときはよく分からなかったけど、改めて見返すと素晴らしい。この記事もかなり影響を受けている。
http://videolectures.net/mlss2011_teh_nonparametrics/ - Toronto大のNealが書いた論文です。今回の記事のことを実装するためには必読。
http://www.stat.columbia.edu/npbayes/papers/neal_sampling.pdf - 実際の実装の載ったtutorial https://datamicroscopes.github.io/
- これだけみてもよく分からないが一度軽く勉強したあと見ると理解が深まる http://mlg.eng.cam.ac.uk/zoubin/talks/uai05tutorial-b.pdf
- Columbiaの先生のホームページ 充実した講義ノートが載っている http://stat.columbia.edu/~porbanz/npb-tutorial.html
- 東大の経済学部の加藤先生が書いたDirichlet過程をしっかり書いたチュートリアル。難しい。
https://docs.google.com/viewer?a=v&pid=sites&srcid=ZGVmYXVsdGRvbWFpbnxra2F0b3N0YXR8Z3g6MmE0NmFkYmU5MzM4YjllNg - Pymcでのノンパラベイズについてのコードがあります。 http://xiangze.hatenablog.com/entry/2016/04/09/225754
- 言わずと知れたBDA http://www.stat.columbia.edu/~gelman/book/
- あともうすぐ出版の佐藤先生のノンパラベイズ本がオススメになると思われます