ガウス過程は、もともとは連続時間確率過程の1つですが、確率モデルとして機械学習への応用されています。
要点としては、ガウス過程とは無限次元の多変量ガウス分布であるということです。
関数だとすると、異なる入力に対する出力の1つ1つがガウス分布に従います。
カーネルで入力の類似度が定義されます。入力が類似していれば出力も類似するようになっており、そのため滑らかな曲線を予測することが出来ます。
別の見方をすると、基底関数をグリッド上に無限に配置した線形回帰モデルとして考えることが出来ます。
観測したデータが与えられると、カーネル行列が計算され、観測されていない場所での平均と分散が決まります。(ガウス分布であることは変化しません。)
計算では、カーネルトリックによって特徴ベクトルを計算することなく出力を得ることが出来ます。
ガウス過程の理論的な説明は「ガウス過程と機械学習(機械学習プロフェッショナルシリーズ)」が参考になります。
また、興味深いことにガウス過程はユニット数が無限のニューラルネットワークと等価であることが分かっています。
今回は前回の記事で導入したPyroでガウス過程を実装してみます。
参考文献
Bingham, E., Chen, J. P., Jankowiak, M., Obermeyer, F., Pradhan, N., Karaletsos, T. et al. (2019).
Pyro: Deep universal probabilistic programming. The Journal of Machine Learning Research, 20(1), 973-978.
コードは以下にあるものを改変して使用しています。
https://github.com/pyro-ppl/pyro (Apache-2.0 License)
Pyroでガウス過程回帰
Pyroの公式チュートリアルの例をやっていきます。
公式ドキュメントも参考になります。
import matplotlib.pyplot as plt
import torch
import pyro
import pyro.contrib.gp as gp
import pyro.distributions as dist
pyro.set_rng_seed(100)
y = 0.5 * sin(3x)から20点を取り出して観測データとします。
N = 20
X = dist.Uniform(0.0, 5.0).sample(sample_shape=(N,))
y = 0.5 * torch.sin(3*X) + dist.Normal(0.0, 0.2).sample(sample_shape=(N,))
plt.plot(X.numpy(), y.numpy(), 'kx')

この20点の観測データから、元の関数(今回ではy = 0.5 * sin(3x)となる)を予測します。
カーネルを決めて、ガウス過程回帰を行います。
# ハイパーパラメータを設定
variance = torch.tensor(0.1)
lengthscale = torch.tensor(0.1)
noise = torch.tensor(0.01)
# 回帰
kernel = gp.kernels.RBF(input_dim=1, variance=variance, lengthscale=lengthscale)
gpr = gp.models.GPRegression(X, y, kernel, noise=noise)
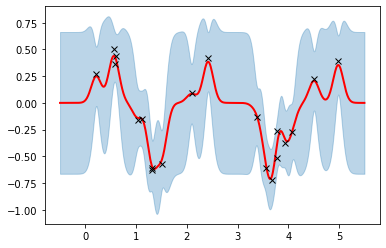
これで回帰ができました。予測結果を表示します。
Xtest = torch.linspace(-0.5, 5.5, 500)
with torch.no_grad():
mean, cov = gpr(Xtest, full_cov=True, noiseless=False)
sd = cov.diag().sqrt()
plt.plot(Xtest.numpy(), mean.numpy(), 'r', lw=2)
plt.fill_between(Xtest.numpy(), (mean - 2.0 * sd).numpy(), (mean + 2.0 * sd).numpy(), color='C0', alpha=0.3)
plt.plot(X.numpy(), y.numpy(), 'kx')
ガウス過程回帰は、上図のように関数の雲(予測曲線の集合)として予測関数が表現されます。
この点はベイズ線形回帰の結果と似てますね。
ただ、この結果はカーネルなどのハイパーパラメータ(variance, lengthscale, noise)が適当に決められた時の結果です。
適切なカーネルのハイパーパラメータに調整するために、変分推論の勾配降下法で最適化します。(MCMCでも可)
optimizer = torch.optim.Adam(gpr.parameters(), lr=0.005)
loss_fn = pyro.infer.Trace_ELBO().differentiable_loss
losses = []
num_steps = 2500
for i in range(num_steps):
optimizer.zero_grad()
loss = loss_fn(gpr.model, gpr.guide)
loss.backward()
optimizer.step()
losses.append(loss.item())
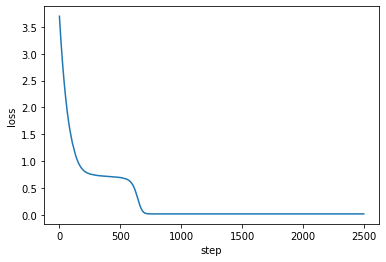
# loss曲線をプロット
plt.plot(losses)
plt.xlabel("step")
plt.ylabel("loss")
# 最適化結果を表示
print('variance = {}'.format(gpr.kernel.variance))
print('lengthscale = {}'.format(gpr.kernel.lengthscale))
print('noise = {}'.format(gpr.noise))
variance = 0.15705525875091553
lengthscale = 0.4686208963394165
noise = 0.017524730414152145
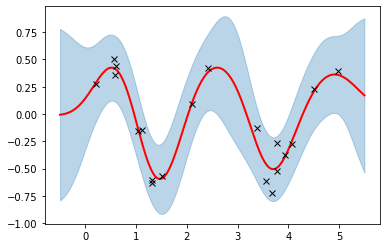
予測結果を表示します。
Xtest = torch.linspace(-0.5, 5.5, 500)
with torch.no_grad():
mean, cov = gpr(Xtest, full_cov=True, noiseless=False)
sd = cov.diag().sqrt()
plt.plot(Xtest.numpy(), mean.numpy(), 'r', lw=2)
plt.fill_between(Xtest.numpy(), (mean - 2.0 * sd).numpy(), (mean + 2.0 * sd).numpy(), color='C0', alpha=0.3)
plt.plot(X.numpy(), y.numpy(), 'kx')
前の図よりも雲の形が滑らかになって、元関数(y = 0.5 * sin(3x))にも近くなりました。
ハイパーパラメータ調整で、予測結果が改善されたと思います。
他の応用
ベイズ最適化
https://pyro.ai/examples/bo.html
回帰で予測関数を出して、探索していきながら最小値を求めることが出来ます(近似解法)。
ガウス過程潜在変数モデル(GPLVM)
https://pyro.ai/examples/gplvm.html
GPLVMは教師なし学習で、出力から入力を求めることで次元削減を行うことが出来ます。
終わりに
通常のデータ解析では、状況にあった確率モデルを自分で決めなければいけません。
例えばベイズ統計モデリングではモデルを定義して事前分布を決めます。
その点ガウス過程ではカーネル(サンプル間の類似度)を指定するのみ良いため、汎用性が高そうです。
そしてそのカーネルさえもARD(関連度自動決定)によって自動的に決定できるようです。
またガウス過程は不確実性も表現できて、少ないサンプルでも柔軟に学習をすることが出来ると思います。
ただしモデルとしては複雑で、解釈が難しいですね。