確率的プログラミング言語は、ベイズ統計モデリングに使われます。
R言語でStanやBUGS、JAGSを使う方法は書籍などがいくつもあって一般的だと思います。
Pythonの確率的プログラミングのライブラリとしては、PyMCやPyStan、TensorFlowの拡張機能であるEdward(現在のTensorFlow Probability)があります。
2018年にはPyroがリリースされました。
PyroはUberが開発しているPyTorchをベースにした確率的プログラミングライブラリです。
最近では同社からJaxをベースにしたNumPyroもリリースされてます。
Pyroの論文:http://jmlr.org/papers/v20/18-403.html
NumPyroの論文:https://arxiv.org/abs/1912.11554
PyroやNumPyroは簡単にベイズ深層学習を実装でき、これから応用されていくのではないでしょうか。(実装した記事)
今回はPyroの公式のチュートリアルから基本的なところをやってみます。
以下のブログ記事も参考にしました。
https://www.hellocybernetics.tech/entry/2019/12/08/033824
https://www.hellocybernetics.tech/entry/2019/12/08/193220
参考文献
Bingham, E., Chen, J. P., Jankowiak, M., Obermeyer, F., Pradhan, N., Karaletsos, T. et al. (2019).
Pyro: Deep universal probabilistic programming. The Journal of Machine Learning Research, 20(1), 973-978.
コードは以下にあるものを改変して使用しています。
https://github.com/pyro-ppl/pyro (Apache-2.0 License)
Pyroのインストール
Pythonは3.4以上で、PyTorchがインストールされていることが前提です。
筆者の環境はUbuntsu16.04、CUDA10、Anaconda、Python3.6、Pytorch1.2.0で行いました。
pip install pyro-ppl
Pyro1.3.1がインストールされました。
また、自動的にPyTorchが1.4.0にアップグレードされました。
実装①:確率分布の定義とサンプリング
インポートとset seedをします。
set seedはサンプリングの再現性のために必要です。
pyro.set_rng_seedをすれば、pytorchでのseed値も決まるようです。
import torch
import pyro
pyro.set_rng_seed(101)
pyro.distributionsはtorch.distributionsと同じようなことができます。
今回はベルヌーイ分布と正規分布で天気と気温を定義します。
def weather():
cloudy = pyro.sample('cloudy', pyro.distributions.Bernoulli(0.3))
cloudy = 'cloudy' if cloudy.item() == 1.0 else 'sunny'
mean_temp = {'cloudy': 55.0, 'sunny': 75.0}[cloudy]
scale_temp = {'cloudy': 10.0, 'sunny': 15.0}[cloudy]
temp = pyro.sample('temp', pyro.distributions.Normal(mean_temp, scale_temp))
return cloudy, temp.item()
これに積み上げてアイスクリームの売上を定義します。つまり階層の確率モデルになります。
def ice_cream_sales():
cloudy, temp = weather()
expected_sales = 200. if cloudy == 'sunny' and temp > 80.0 else 50.
ice_cream = pyro.sample('ice_cream', pyro.distributions.Normal(expected_sales, 10.0))
return ice_cream
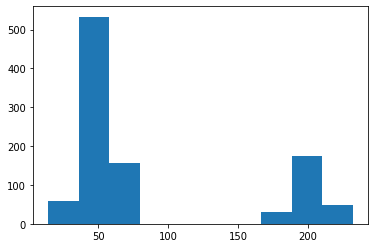
アイスクリームの売上をサンプリングしてヒストグラムで表してみます。
import matplotlib.pyplot as plt
N = 1000 #サンプル数
x_list = []
for _ in range(N):
x = ice_cream_sales()
x_list.append(x)
plt.hist(x_list)
pyro.plateメソッドでベクトル化
pyro.plateメソッドを使えばベクトル化によってfor文で繰り返さないでサンプリングできるようです。
独立同分布から並列的にサンプリングが行われるということです。
今までのコードをpyro.plateを使って書き換えてみました。
モデルの定義
def model(N):
with pyro.plate("plate", N):
cloudy = pyro.sample('cloudy', pyro.distributions.Bernoulli(0.3))
mean_temp = 75.0 - 20.0 * cloudy
scale_temp = 15.0 - 5.0 * cloudy
temp = pyro.sample('temp', pyro.distributions.Normal(mean_temp, scale_temp))
expected_sales = 50.0 + 150.0 * (1 - cloudy) * (temp > 80.0)
ice_cream = pyro.sample('ice_cream', pyro.distributions.Normal(expected_sales, 10.0))
return ice_cream
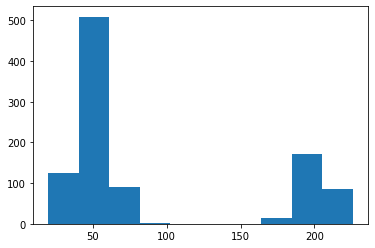
ヒストグラムを表示します。
import matplotlib.pyplot as plt
N = 1000 #サンプル数
x_list = model(N)
plt.hist(x_list)
同じようなヒストグラムになりました。少し違いがあるのは、ベクトル化による並列でサンプリングした影響でしょうか?
pyroの重要な特徴としてpyro.sample("hoge", dist)のように、第一引数で変数名を指定しています。これは、グローバルな確率変数であることを定義するために必要であるようです。(詳細はよく分かりません。)
実装②:ベイズ推論
前項で確率モデルからデータを生成する方法がわかりました。
本項でデータから確率モデルを推論する方法をやってみます。
import torch
import pyro
pyro.set_rng_seed(101)
import matplotlib.pyplot as plt
データとして、1の値×6個と0の値×4個の、計10個のデータを用意します。
data = []
for _ in range(6):
data.append(torch.tensor(1.0))
for _ in range(4):
data.append(torch.tensor(0.0))
data = torch.tensor(data) #Pyroで扱うためにtensor化する
plt.hist(data)
このデータに対して、確率分布をモデリングします。
今回はベータ分布に従うパラメータ"latent_fairness"を持つベルヌーイ分布で考えます。
import pyro.distributions as dist
def model(data):
alpha0 = torch.tensor(10.0)
beta0 = torch.tensor(10.0)
f = pyro.sample("latent_fairness", dist.Beta(alpha0, beta0))
with pyro.plate("data_plate"):
pyro.sample("obs", dist.Bernoulli(f), obs=data)
このモデルに当てはまるようなパラメータを推論します。
推論の方法はいくつかありますが、変分ベイズとMCMCが主な方法です。
変分ベイズ
推論手法の中でも、Pyroでは変分ベイズの機能が一番充実しているようです。
これは、PyroのベースであるPyTorchの自動微分や最適化手法が変分ベイズのSVI(確率的変分推論)に使用されるためであると思われます。
まずは変分近似分布を用意します。
自分で定義することもできますが、pyro.infer.autoguide.guidesクラスで自動的に行うこともできます。
guide = pyro.infer.autoguide.guides.AutoDelta(model)
変分推論を実行します。
from pyro.optim import Adam
from pyro.infer import SVI, Trace_ELBO
adam_params = {"lr": 0.0005, "betas": (0.90, 0.999)}
optimizer = Adam(adam_params)
pyro.clear_param_store()
svi = SVI(model, guide, optimizer, loss=Trace_ELBO())
n_steps = 1000 #ステップ数
losses, f = [], [] #後でplotするための記録用
for step in range(n_steps):
loss = svi.step(data)
losses.append(loss)
f.append(pyro.param("AutoDelta.latent_fairness").item())
これで推論ができました。
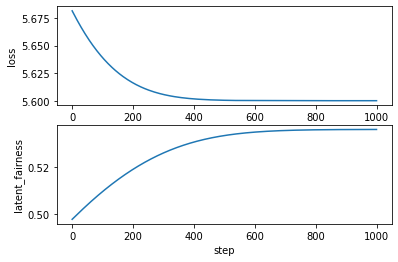
経過をプロットします。
plt.subplot(2,1,1)
plt.plot(losses)
plt.xlabel("step")
plt.ylabel("loss")
plt.subplot(2,1,2)
plt.plot(f)
plt.xlabel("step")
plt.ylabel("latent_fairness")
パラメータ"latent_fairness"は約0.5357に収束していきました。
最終的な値は以下で表示できます。
for name in pyro.get_param_store():
print("{}: {}".format(name, pyro.param(name)))
AutoDelta.latent_fairness: 0.535700261592865
推論したモデルから予測確率分布を表示します。
1000個のサンプルを取り出します。
from pyro.infer import Predictive
predictive_dist = Predictive(model=model, guide=guide,num_samples=1000, return_sites=["obs"])
plt.hist(predictive_dist.get_samples(None)["obs"].view(1,-1))
データのヒストグラムと同じような分布になりました。(若干違うのは元々のデータ数が10と少ないからでしょうか?)
MCMC
MCMCは力技的な手法で時間がかかります。
from pyro.infer import NUTS, MCMC
nuts_kernel = NUTS(model)
mcmc = MCMC(nuts_kernel, num_samples=5000, warmup_steps=1000)
mcmc.run(data)
これで推論ができました。
結果を見ます。
mcmc.summary()
| parameter | mean | std | median | 5.0% | 95.0% | n_eff | r_hat |
|---|---|---|---|---|---|---|---|
| latent_fairness | 0.53 | 0.09 | 0.54 | 0.38 | 0.68 | 1894.58 | 1.00 |
MCMCではposterior_samplesにパラメータのサンプルを渡すことで予測確率分布を表せます。
f_mcmc = mcmc.get_samples()["latent_fairness"]
from pyro.infer import Predictive
predictive_dist = Predictive(model=model, posterior_samples={"latent_fairness": f_mcmc}, return_sites=["obs"])
plt.hist(predictive_dist.get_samples(None)["obs"].view(1,-1))
こちらもデータのヒストグラムと同じような分布になりました。
他の推論方法
MAP推定やラプラス近似があります。
MAP推定はベイズ推論の特殊形で、点推定であるため確率分布は求められません。
確率分布を求めないから推論(inference)ではなくて推定(estimation)なんですね。(参考記事)
*上記で行った変分ベイズは変分近似分布としてデルタ分布を選んでいるため、MAP推定と等価です。
ラプラス近似は、autoguideのAutoLaplaceApproximationで出来るようです。
応用事項
混合ガウスモデル、ガウス過程、ベイズ最適化、NMF、カルマンフィルタ、隠れマルコフモデルなど様々なことが出来るようです。
終わりに
まだPyroを始めたばかりですが、なんとなく使い方がわかってきました。
数式では難しい理論をここまで簡潔に実装できるのは素晴らしい技術だと思います。