今回は,確率的プログラミング言語『Pyro』を使って2層ベイズニューラルネットワークモデルに対して変分推論(平均場近似),ラプラス近似,MCMC(NUTS)の3つの手法を試してみました.
『ベイズ深層学習』第5章5.1節の図5.2のデータを使います.
環境
Python 3.7.5
PyTorch 1.3.0
Pyro 0.5.1
ソースコード
今回のソースコードはGitHub上(こちら)に上げました.
ベイズニューラルネットワークモデル
入力の次元を$H_{0}$, 出力の次元を$D$とするデータ集合$\mathcal{D} = \{ \mathbf{x}_n, \mathbf{y}_n \}_{n = 1}^{N}$が与えられたとします.ただし,データは$\mathcal{i.i.d}$であると仮定します.
この時,入力$\mathbf{x}_n \in \mathbb{R}^{H_{0}}$に対する出力$\mathbf{y}_n \in \mathbb{R}^{D}$を予測する回帰問題を考えます.
ここで,回帰モデルとして,次のベイズニューラルネットワークモデルを仮定しようと思います.
観測モデルは, $$ p\left( \mathbf{y}_n | \mathbf{x}_n, \mathbf{W} \right) = \mathcal{N}\left(
\mathbf{y}_n | \mathbf{f}(\mathbf{x}_n ; \mathbf{W}), \sigma_y^2\mathbf{I} \right) $$ ここで,$\mathbf{f}(\mathbf{x}_n ; \mathbf{W})$はパラメータを$\mathbf{W}$としたニューラルネットワークです.
パラメータ$\mathbf{W}$の事前分布は, $$ p(\mathbf{W}) = \prod_{l=1}^{L}\prod_{i=1}^{H_{l}}\prod_{j=1}^{H_{l-1}}\mathcal{N}(w_{i,j}^{(l)} | 0, \sigma_w^2) $$
ここで,$L$はニューラルネットワークの層の数,$H_l$は第$l$層のユニット数で,$H_L = D$です.
以上より,入力データ$ \mathbf{X} = \{ \mathbf{x}_1, \ldots, \mathbf{x}_N \} $が与えられたもとでの,観測データ$ \mathbf{Y} = \{ \mathbf{y}_1, \ldots, \mathbf{y}_N \} $とパラメータ$\mathbf{W}$の同時分布は,
\begin{align}
p(\mathbf{Y}, \mathbf{W} | \mathbf{X})
&= p(\mathbf{W})\prod_{n=1}^{N}p\left( \mathbf{y}_n | \mathbf{x}_n, \mathbf{W} \right) \\
&= \left\{\prod_{l=1}^{L}\prod_{i=1}^{H_{l}}\prod_{j=1}^{H_{l-1}}\mathcal{N}(w_{i,j}^{(l)} | 0, \sigma_w^2)\right\}\prod_{n=1}^{N}\mathcal{N}\left(
\mathbf{y}_n | \mathbf{f}(\mathbf{x}_n ; \mathbf{W}), \sigma_y^2\mathbf{I} \right)
\end{align}
となります.
ニューラルネットワークの仮定
今回は,$L = 2$,$D = 1$,活性化関数$\phi$を双曲線正接関数としたニューラルネットワークを考えることにします.
f(\mathbf{x}_n ; \mathbf{W}) = \sum_{h_{1}=1}^{H_{1}} w_{h_{1}}^{(2)} {\rm Tanh} \left( \sum_{h_{0}=1}^{H_{0}} w_{h_{1}, h_{0}}^{(1)} x_{n, h_{0}} \right)
実装
確率的プログラミング言語『Pyro』を利用して実装を行います.
Pyroについて全く知識のない方は,公式チュートリアルやHELLO CYBERNETICSさんの記事等をご覧になると良いと思います.
以下のコードでは自作クラスを用いているため,selfがたくさん出てきて見づらいかもしれませんがご容赦ください.BNNクラスがベイズニューラルネットワークモデルのクラスとなっています.
コードの説明が長々と続くため,結果だけ見たい方はこの節は飛ばしてください.
共通事項
各層の次元
データは入出力共に1次元のものを使いますが,バイアス項を導入するために,入力ベクトルは$(x, 1)^{\top}$と,2次元に拡張します.
H_0 = 2 # 入力次元
H_1 = 4 # 中間層のユニット数
D = 1 # 出力次元
訓練データセット
『ベイズ深層学習』第5章5.1節の図5.2のデータを読み取って使うことにします.
# data
data = torch.tensor([[-4.5, -0.22],
[-4.4, -0.10],
[-4.0, 0.00],
[-2.9, -0.11],
[-2.7, -0.33],
[-1.5, -0.20],
[-1.3, -0.08],
[-0.8, -0.21],
[0.1, -0.34],
[1.5, 0.10],
[2.0, 0.11],
[2.1, 0.14],
[2.6, 0.21],
[3.5, 0.23],
[3.6, 0.38]])
x_data = data[:, 0].reshape(-1, 1)
x_data = torch.cat([x_data, torch.ones_like(x_data)], dim=1) # biasごと入力に含ませる
y_data = data[:, 1]
plotしてみます.
ハイパーパラメータ
比較のため,ハイパーパラメータは各手法で以下の共通の値とします.
w_sigma = torch.tensor(0.75)
y_sigma = torch.tensor(0.09)
変分推論
まず,変分推論によるベイズ推論をベイズニューラルネットワークモデルに適用してみます.
今回は,変分推論の中でも最もシンプルな,平均場近似を採用してみます.
ライブラリのimport
必要なライブラリをimportします.
import matplotlib.pyplot as plt
import torch
import pyro
from pyro.distributions import Normal, Delta
from pyro.infer.autoguide.guides import AutoDiagonalNormal
from pyro.infer import SVI, Trace_ELBO
from pyro.optim import Adam
from pyro.infer.predictive import Predictive
生成モデル
確率的プログラミング言語であるPyroのフレームワークでモデルの記述を行うことで,SVIクラスを利用して変分推論を簡単に行うことができます.
def model(self, x_data, y_data):
# パラメータの生成
with pyro.plate("w1_plate_dim2", self.hidden_size):
with pyro.plate("w1_plate_dim1", self.input_size):
w1 = pyro.sample("w1", Normal(0, self.w_sigma))
with pyro.plate("w2_plate_dim2", self.output_size):
with pyro.plate("w2_plate_dim1", self.hidden_size):
w2 = pyro.sample("w2", Normal(0, self.w_sigma))
f = lambda x: torch.mm(torch.tanh(torch.mm(x, w1)), w2)
# 観測データの生成
with pyro.plate("map", len(x_data)):
prediction_mean = f(x_data).squeeze()
pyro.sample("obs", Normal(prediction_mean, self.y_sigma), obs=y_data)
return prediction_mean
Pyroでは,自分の定めた確率的生成モデルをmodelという関数にて記述します.
記述の仕方としては,各確率変数の従う分布からサンプルを生成していくように記述していきます.
サンプルの生成には,pyro.sample(site_name, distribution)を使います.
確率変数の名前をsite_nameで,確率変数の従う分布をdistributionで指定することで,サンプルが生成されます.
また,pyro.plateというコンテキストマネージャが存在します.このwithステートメント内では独立にサンプルが生成されることになります.したがって,独立性を仮定している場合はpyro.plateを使いましょう.
変分モデル
Pyroで変分推論を行う場合,変分モデルも記述する必要があります.modelと同様に各確率変数に関して近似分布を記述してサンプルを生成させても良いのですが,pyro.infer.autoguide.guides.AutoGuideクラスを使うことで,典型的な変分モデルであれば自動的に用意してくれます.
self.guide = AutoDiagonalNormal(self.model)
今回はパラメータの近似分布としてAutoDiagonalNormal,つまり対角ガウス分布を使います.これによって,すべてのパラメータが完全独立分解近似されます.従って,平均場近似を行っていることになります.
推論
生成モデル(model)と変分モデル(guide)を定義したので,準備は完了です.
実際に変分推論をしていきます.
def VI(self, x_data, y_data, num_samples=1000, num_iterations=30000):
self.guide = AutoDiagonalNormal(self.model)
optim = Adam({"lr": 1e-3})
loss = Trace_ELBO()
svi = SVI(self.model, self.guide, optim=optim, loss=loss)
# train
pyro.clear_param_store()
for j in range(num_iterations):
loss = svi.step(x_data, y_data)
if j % (num_iterations // 10) == 0:
print("[iteration %05d] loss: %.4f" % (j + 1, loss / len(x_data)))
# num_samplesだけ事後分布からサンプルを生成
dict = {}
for i in range(num_samples):
sample = self.guide() # sampling
for name, value in sample.items():
if not dict.keys().__contains__(name):
dict[name] = value.unsqueeze(0)
else:
dict[name] = torch.cat([dict[name], value.unsqueeze(0)], dim=0)
self.posterior_samples = dict
まずはじめに,変分推論をどのような設定で行うかを定めるために,SVIクラスのインスタンスを生成します(SVI(model, guide, optim, loss, ...)).引数としては,生成モデルmodel,変分モデルguide,最適化手法optim,損失関数lossを渡す必要があります.
最適化手法はAdamを,損失関数は変分下界ELBO(の-1倍)を利用します.
後は,svi.step(x_data, y_data)によって近似分布を真の事後分布に近づけていきます.
近似事後分布が求まったら,num_samplesだけ事後分布からパラメータをサンプリングして,self.posterior_samplesにサンプルの辞書を格納します.
予測
事後分布の推論が完了したので,事後予測分布を推論してみます.
Pyroでは,事後予測分布からのサンプルを生成することもできます.
def predict(self, x_pred):
def wrapped_model(x_data, y_data):
pyro.sample("prediction", Delta(self.model(x_data, y_data)))
predictive = Predictive(wrapped_model, self.posterior_samples)
samples = predictive.get_samples(x_pred, None)
return samples["prediction"], samples["obs"]
ここで,$y$の予測分布だけでなく,$y$の平均,つまりニューラルネットワークの出力$f$の予測分布も取得してみることにしましょう.
modelで返り値としていた$y$の平均prediction_meanを,その点でのみ$\infty$の確率密度を持つ分散$0$の分布に従う確率変数として,modelをラッピングしたwrapped_modelを新たに定義しました.
これによって,$y$の平均も確率変数として扱うことができるようになり,予測分布を求めることができます.
Predictive(model, posterior_samples).get_samples(x_pred, None)で,事後予測分布からのサンプルを得ることができます.
今回は,$y$("obs")とその平均("prediction")の事後予測分布からのサンプルを取得しています.
結果の図示
それでは,予測結果を図示してみましょう.
左は$y$の平均,つまりニューラルネットワークの出力$f$の予測分布からのサンプルです.
右は$y$の予測分布からのサンプルです.$y$の分散を考慮しているので左に比べて分散が大きくなっていることがわかります.
どちらも緩やかな予測曲線を描いていますね.
ラプラス近似
次は,ラプラス近似を適用してみます.
pyro.infer.autoguide.guidesにはラプラス近似を行えるAutoLaplaceApproximationクラスが存在しますが,使い方が間違っているのか望ましい結果が出せなかったので,MAP推定をPyroで行い,そこからはPyTorchの自動微分を利用して実装を行いました.
ライブラリのimport
必要なライブラリをimportします.
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import pyro
from pyro.distributions import Normal
from pyro.infer.autoguide.guides import AutoDelta
from pyro.infer import SVI, Trace_ELBO
from pyro.optim import Adam
生成モデル
後に利用するため,PyTorchのニューラルネットワークモデルをまず用意します.
# バイアス項なし全結合Layerを定義
class NonBiasLinear(nn.Module):
def __init__(self, input_size, output_size):
super(NonBiasLinear, self).__init__()
self.weight = nn.Parameter(data=torch.randn(input_size, output_size), requires_grad=True)
def forward(self, input_tensor):
return torch.mm(input_tensor, self.weight)
# 2層ニューラルネットワークモデル
class Net(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(Net, self).__init__()
self.fc1 = NonBiasLinear(input_size, hidden_size)
self.fc2 = NonBiasLinear(hidden_size, output_size)
def forward(self, x):
output = self.fc1(x)
output = torch.tanh(output)
output = self.fc2(output)
return output
Pyroでは,PyTorchのnn.Moduleクラスで記述した決定論的なモデルをpyro.random_moduleによって確率的生成モデルへと"lift"することができます.ただし,決定論的なモデルから確率的生成モデルにするために,各確率変数の分布を記述する必要があることには注意してください.
def model(self, x_data, y_data):
# 事前分布
w1_size = (self.input_size, self.hidden_size)
w2_size = (self.hidden_size, self.output_size)
w1_prior = Normal(torch.zeros(size=w1_size), self.w_sigma * torch.ones(size=w1_size))
w2_prior = Normal(torch.zeros(size=w2_size), self.w_sigma * torch.ones(size=w2_size))
priors = {'fc1.weight': w1_prior, 'fc2.weight': w2_prior}
# lift
lifted_module = pyro.random_module("module", self.net, priors)
lifted_bnn_model = lifted_module()
with pyro.plate("map", len(x_data)):
prediction_mean = lifted_bnn_model(x_data).squeeze()
pyro.sample("obs", Normal(prediction_mean, self.y_sigma), obs=y_data)
return prediction_mean
推論
ラプラス近似では,まずMAP推定値を計算し,それから後述する式を計算して近似事後分布を求めます.
ラプラス近似によるベイズ推論の理論の詳細に関しては,『ベイズ深層学習』4.2.3節や,5.1.2節を参照してください.
まず,MAP推定値を求めます.AutoDeltaクラスを利用すれば,Pyroの変分推論の枠組みでMAP推定値を得ることができます.
# MAP推定
def MAPestimation(self, x_data, y_data, num_iterations=10000):
guide = AutoDelta(self.model)
svi = SVI(self.model, guide, Adam({"lr": 1e-3}), loss=Trace_ELBO())
# train
pyro.clear_param_store()
for j in range(num_iterations):
loss = svi.step(x_data, y_data)
if j % (num_iterations // 10) == 0:
print("[iteration %05d] loss: %.4f" % (j + 1, loss / len(x_data)))
# MAP推定値を取得
param_dict = {}
for name, value in pyro.get_param_store().items():
param_dict[name] = value.data
w1_MAP = param_dict['auto_module$$$fc1.weight']
w2_MAP = param_dict['auto_module$$$fc2.weight']
self.net.fc1.weight.data = w1_MAP
self.net.fc2.weight.data = w2_MAP
return w1_MAP, w2_MAP
求まったMAP推定値$\mathbf{W}_{\rm MAP}$に対して,ラプラス近似によるパラメータ$\mathbf{W}$の近似事後分布は,
q(\mathbf{W}) = \mathcal{N}(\mathbf{W} | \mathbf{W}_{\rm MAP}, \left\{ \mathbf{\Lambda}(\mathbf{W}_{\rm MAP}) \right\}^{-1})
となります.ただし,$\mathbf{W}, \mathbf{W}_{\rm MAP}$は重みパラメータを1列に並べた列ベクトルの形になっているものとします.
ここで,精度行列$\mathbf{\Lambda}$は,
\begin{align}
\mathbf{\Lambda}
&= - \nabla_{\mathbf{W}}^2 \ln{p(\mathbf{W} | \mathbf{Y}, \mathbf{X})} \\
&= \frac{1}{\sigma_{y}^{2}} \mathbf{I} + \frac{1}{\sigma_{w}^{2}} \nabla_{\mathbf{W}}^2 E(\mathbf{W}) \\
&\approx \frac{1}{\sigma_{y}^{2}} \mathbf{I} + \frac{1}{\sigma_{w}^{2}} \sum_{n=1}^{N} \left( \nabla_{\mathbf{W}}\mathbf{a}_{n}^{(L)} \right) \left( \nabla_{\mathbf{W}}\mathbf{a}_{n}^{(L)} \right)^\top
\end{align}
と近似します.ここで,ヘッセ行列の計算に『ベイズ深層学習』p.34 式(2.58)の近似を用いることにしました.
# ヘッセ行列の計算
def _compute_hessian(self, x_data, hessian_size):
hessian_matrix = torch.zeros(size=(hessian_size, hessian_size))
for x in x_data:
x.unsqueeze_(0)
f = self.net.forward(x)
f.backward(retain_graph=False)
with torch.no_grad():
grad_w1 = self.net.fc1.weight.grad
grad_w2 = self.net.fc2.weight.grad
grad_f = torch.cat([grad_w1.reshape(-1, 1), grad_w2.reshape(-1, 1)], dim=0) # 勾配(列ベクトル)の形に整形
hessian_matrix += torch.mm(grad_f, torch.t(grad_f))
self.net.zero_grad() # 勾配を0に戻す
return hessian_matrix
# ラプラス近似分布の計算
def LaplaceApproximation(self, x_data, y_data):
# 平均ベクトルについて
w1_MAP, w2_MAP = self.MAPestimation(x_data, y_data)
W_MAP_vector = torch.cat([w1_MAP.reshape(-1, 1), w2_MAP.reshape(-1, 1)], dim=0)
# 共分散行列について
M = W_MAP_vector.shape[0]
hessian_matrix = self._compute_hessian(x_data, hessian_size=M)
lambda_matrix = (self.w_sigma ** (-2)) * torch.eye(M) + (self.y_sigma ** (-2)) * hessian_matrix
self.lambda_mat_inv = torch.inverse(lambda_matrix)
予測
パラメータ$\mathbf{W}$の事後分布が求まったら,新規入力点$\mathbf{x}_{\ast}$に対する出力$y_{\ast}$の事後予測分布を求めます.
この事後予測分布を,
p(y_{\ast} | \mathbf{x}_{\ast}, \mathbf{Y}, \mathbf{X})
\approx \mathcal{N}(y_{\ast} | f(\mathbf{x}_{\ast} ; \mathbf{W}_{\rm MAP}), \sigma_y^2+\mathbf{g}^\top \left\{ \mathbf{\Lambda}(\mathbf{W}_{\rm MAP}) \right\}^{-1} \mathbf{g})
と近似します.ただし,$ \mathbf{g} = \nabla_{\mathbf{W}} f(\mathbf{x}_{\ast} ; \mathbf{W}) \mid _{\mathbf{W} = \mathbf{W}_{\rm MAP}} $と置いています.
# 事後予測分布の計算
def predict(self, x_pred):
f_pred = self.net.forward(x_pred)
f_pred.backward(retain_graph=False)
with torch.no_grad():
grad_w1 = self.net.fc1.weight.grad
grad_w2 = self.net.fc2.weight.grad
g = torch.cat([grad_w1.reshape(-1, 1), grad_w2.reshape(-1, 1)], dim=0)
y_pred_sigma2 = self.y_sigma ** 2 + torch.mm(torch.t(g), torch.mm(self.lambda_mat_inv, g)) # 予測分散
self.net.zero_grad() # 勾配を0に戻す
return f_pred, torch.sqrt(y_pred_sigma2)
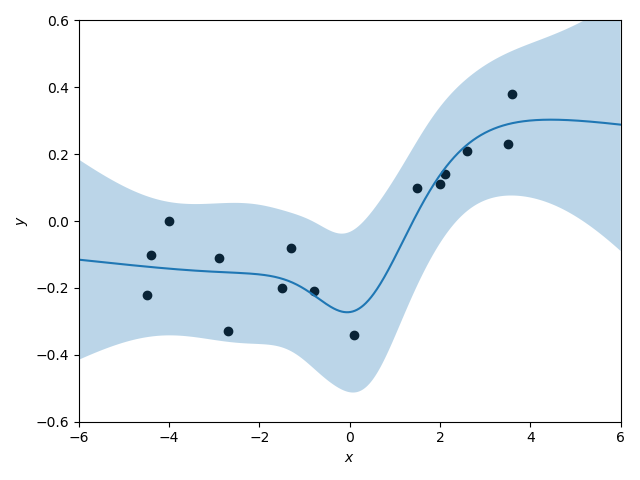
結果の図示
それでは,こちらも予測結果を図示してみましょう.
こちらは解析的な計算に基づいて$y$の分布のパラメータを求めていますので,平均の曲線と分散の2倍の予測区間を図示しました.
先ほどの平均場近似に比べて,複雑度の高い予測曲線となっているように思われます.
MCMC
最後にMCMCを適用してみましょう.
ライブラリのimport
必要なライブラリをimportします.
import matplotlib.pyplot as plt
import torch
import pyro
from pyro.distributions import Normal, Delta
from pyro.infer.mcmc.api import MCMC
from pyro.infer.mcmc.nuts import NUTS
from pyro.infer.mcmc.util import predictive
生成モデル
生成モデルは先ほどの変分推論の時と同じですので省略します.
推論
MCMCの手法のうち,今回はHMCの発展版であるNUTSを使います.
def nuts_sampling(self, x_data, y_data, num_samples, warmup_steps):
nuts_kernel = NUTS(self.model, target_accept_prob=0.99)
mcmc = MCMC(nuts_kernel, num_samples=num_samples, warmup_steps=warmup_steps)
mcmc.run(x_data, y_data)
self.posterior_samples = mcmc.get_samples()
MCMC(kernel, num_samples, warmup_steps, ...)としてインスタンスを生成し,runメソッドを呼び出すことでMCMCサンプリングが行われます.
その後,get_samplesメソッドを呼び出すことで生成したサンプルを取得できます.
予測
def predict(self, x_pred):
def wrapped_model(x_data, y_data):
pyro.sample("prediction", Delta(self.model(x_data, y_data)))
samples = predictive(wrapped_model, self.posterior_samples, x_pred, None)
return samples["prediction"], samples["obs"]
MCMCによる事後分布の推論をした後の予測分布の求め方は,変分推論の時とほぼ同じです.おそらく正式リリースの時には統合されていると思いますが,現在,MCMCではPredictiveではなくpredictiveを使います.
結果の図示
こちらも結果を図示してみましょう.
変分推論の時と同様,左は$y$の平均,右は$y$の予測分布です.
複雑度の高い予測分布が得られています.
比較
最後に,3つの手法の比較を行います.
実行速度
変分推論(VI),ラプラス近似(LA),MCMCそれぞれに対して,推論にかかった時間を測定しました.(各1回しか測定してないので目安程度ですが)
time: 93.1693[sec]
time: 19.8220[sec]
sample: 100%|██████████| 1500/1500 [25:57, 1.04s/it, step size=9.50e-03, acc. prob=0.984]
MCMCに関しては,PyroでMCMCを走らせることで上記のように表示が出ます.25分57秒かかっているようです.
最適化による推論アルゴリズムである変分推論とラプラス近似が非常に高速であることがわかります.変分推論よりラプラス近似が速いのは,最適化ステップ数が少ないためです.
精度
もう一度,各手法の予測分布の図を載せます.
MCMCは,理論的には真の事後分布からのサンプリングが可能であり,図をみても最も正確に予測分布からのサンプリングができていそうです.一方,変分推論やラプラス近似は,近似によって表現能力が制限されていることが見て取れます.特に,変分推論では平均場近似をしたので,とても制限されたものになっています.
まとめ
今回扱ったモデルは,たった2層のベイズニューラルネットワークモデルであり,隠れユニット数も4つと,ニューラルネットワークとしては単純なモデルです.データサイズもたった15です.それでもMCMCは収束までに結構時間がかかりました.より複雑なベイズモデルを学習させるのには,ミニバッチを利用するなどの計算時間削減の工夫が必須であることを体感できました.
参考文献
『ベイズ深層学習』
『Pyro Documentation』(Pyroの公式ドキュメント)
『Welcome to Pyro Examples and Tutorials!』(Pyroの公式チュートリアル)
『確率的プログラミング言語Pyroと変分ベイズ推論の基本』(HELLO CYBERNETICSさんの記事)