東京大学・株式会社Nospareの菅澤です.
前回の記事で,馬蹄事前分布(horseshoe prior)について紹介しました.今回は馬蹄事前分布を使った線形回帰モデルとその推定のためのMCMCアルゴリズムについて紹介していきます.
線形回帰モデルと馬蹄事前分布
線形回帰モデル
y=X\beta + \varepsilon, \ \ \ \ \varepsilon\sim N(0,\sigma^2 I_n)
の回帰係数ベクトル$\beta=(\beta_1,\ldots,\beta_p)^{\top}$の各要素に対する馬蹄事前分布は
\beta_k \ | \ \lambda_k\sim N(0, \lambda_k^2\tau^2\sigma^2), \ \ \ \ \lambda_k\sim C^{+}(0,1), \ \ \ \ k=1,\ldots,p
で表現されます.簡単のため,回帰モデルにおける分散パラメータ$\sigma^2$には逆ガンマ事前分布$\sigma^2\sim {\rm IG}(a_{\sigma}, b_{\sigma})$を用います.
ここで$a_{\sigma}, b_{\sigma}$は固定したハイパーパラメータです.(以下の数値例では$a_{\sigma}=b_{\sigma}=1$を用います.)
この事前分布は条件付き共役となり,後述のように$\sigma^2$の完全条件付き分布も逆ガンマ分布となります.
$\tau^2$の事前分布としては$\lambda_k$と同様に半コーシー分布$C^{+}(0,1)$を用いることが推奨されています.
少し話は逸れますが,階層モデルにおける($\tau^2$のような)スケールパラメータの妥当な事前分布に関する研究(Gelman (2006)やPolson and Scott (2012)など)で,
半コーシー分布は逆ガンマ分布に替わる事前分布として推奨されています.
馬蹄事前分布の階層表現
馬蹄事前分布を用いてMCMCを実行するにあたり,$\beta_k$と$\lambda_k$の完全条件付き分布からサンプリングする必要があります.Bayesian Lassoの記事でも紹介したように,$\beta_k$の条件付き事前分布は正規分布になってますので,その完全条件付き分布も正規分布になります.では$\lambda_k$の完全条件付き分布はどうでしょうか?
馬蹄事前分布の定義から$\lambda_k$の完全条件付き分布は以下に比例することがわかります.
\frac{1}{\lambda_k(1+\lambda_k^2)}\exp\left(-\frac{\beta_k^2}{2\lambda_k\tau^2\sigma^2}\right), \ \ \ \ \lambda_k>0.
これは馴染みのある分布でないため,この分布からのサンプリングは必ずしも自明ではありません.しかし,$\lambda_k$の事前分布に追加的な階層構造を導入することで,より簡単に$\lambda_k$のサンプリングを実行することができます.実は以下のような関係が成り立ちます.
\lambda_k\sim C^{+}(0,1) \ \ \ \ \Leftrightarrow \ \ \ \ \lambda_k^2\ | \ \nu_k\sim {\rm IG}\left(\frac12, \frac1{\nu_k}\right), \ \ \ \nu_k\sim {\rm IG}\left(\frac12, 1\right)
上記の表現を用いると,馬蹄事前分布は三段階の階層によって表されることがわかります.
\beta_k\ | \ \lambda_k\sim N(0, \lambda_k^2\tau^2\sigma^2), \ \ \ \ \lambda_k^2\ | \ \nu_k\sim {\rm IG}\left(\frac12, \frac1{\nu_k}\right), \ \ \ \nu_k\sim {\rm IG}\left(\frac12, 1\right), \ \ \ \ k=1,\ldots,p.
また,$\tau^2$の事前分布に関しても同様の階層表現
\tau^2\ | \ \xi\sim {\rm IG}\left(\frac12, \frac1{\xi}\right), \ \ \ \xi\sim {\rm IG}\left(\frac12, 1\right)
を用います.
ギブスサンプリングによるMCMC
馬蹄事前分布の階層表現を用いることで,全てのパラメータの同時事後分布は以下のような形になります.
\pi(\beta,\sigma^2,\lambda,\nu,\tau^2,\xi \ | \ y)\propto
\exp\left\{-\frac{1}{2\sigma^2}(y-X\beta)^T(y-X\beta)-\frac{1}{2\sigma^2\tau^2}\sum_{k=1}^p\frac{\beta_k^2}{\lambda_k^2}-\sum_{k=1}^p\frac{1}{\nu_k}\left(1+\frac{1}{\lambda_k^2}\right)\right\}\\
\times (\sigma^2)^{-(n+p)/2-a_\sigma-1}(\tau^2)^{-(p+1)/2-1}\xi^{-2}\left\{\prod_{k=1}^p (\lambda_k^2)^{-2}\nu_k^{-2}\right\}\exp\Big(-\frac{b_{\sigma}}{\sigma^2}-\frac{1}{\xi\tau^2}-\frac{1}{\xi}\Big).
したがって各パラメータの完全条件付き分布が以下のように求まります.
-
$\beta$の完全条件付き分布: $N(A^{-1}X^Ty, \sigma^2 A^{-1})$.ただし$A=X^TX+D$, $D={\rm diag}(\lambda_1^{-2},\ldots,\lambda_p^{-2})/\tau^2$.
-
$\sigma^2$の完全条件付き分布: ${\rm IG}(\ a_\sigma+(n+p)/2, \ b_\sigma+(y-X\beta)^T(y-X\beta)/2+\beta^TD\beta/2 \ )$.
-
$\lambda_k^2$の完全条件付き分布: ${\rm IG}(1, 1/\nu_k+\beta_k^2/2\tau^2\sigma^2)$.
-
$\nu_k$の完全条件付き分布: ${\rm IG}(1, 1+1/\lambda_k^2)$.
-
$\tau^2$の完全条件付き分布: ${\rm IG}((p+1)/2, 1/\xi+\sum_{k=1}^p \beta_k^2/2\sigma^2\lambda_k^2)$.
-
$\xi$の完全条件付き分布: ${\rm IG}(1, 1+1/\tau^2)$.
このように各パラメータの完全条件付き分布は全て標準的な分布になり,簡単にMCMCが実行できます.
Rでのデモ
馬蹄事前分布を用いた際のギブスサンプリングを実装したものが以下のコードです.
HS.Gibbs <- function(Y, X, mc=2000, burn=500, sig.prior=c(1,1)){
## preparation
XX <- cbind(1, X)
n <- dim(XX)[1]
p <- dim(XX)[2]
a.sig <- sig.prior[1]
b.sig <- sig.prior[2]
## vectors/matrices to store posterior samples
Beta.pos <- matrix(NA, mc, p)
Sig.pos <- rep(NA, mc)
Tau.pos <- rep(NA, mc)
Lam.pos <- matrix(NA, mc, p)
## initial values
init.fit <- lm(Y~X)
Beta <- coef(init.fit)
Sig <- summary(init.fit)$sigma
Tau <- 1
Lam <- rep(1, p) # latent variable for beta
Nu <- rep(1, p) # latent variable for lambda
mat <- t(XX)%*%XX
Xi <- 1 # latent variable for tau
## MCMC
for(k in 1:mc){
# Beta
invA <- solve( mat + diag(1/Lam^2)/Tau^2 )
hbeta <- as.vector( invA%*%t(XX)%*%Y )
Beta <- mvrnorm(1, hbeta, Sig^2*invA)
Beta.pos[k,] <- Beta
# Sigma
resid <- as.vector( Y-XX%*%Beta )
at.sig <- a.sig + 0.5*(n+p)
bt.sig <- b.sig + 0.5*sum(resid^2) + 0.5*sum(Beta^2/(Lam^2*Tau^2))
Sig <- sqrt( rinvgamma(1, at.sig, bt.sig) )
Sig.pos[k] <- Sig
# Lam
Lam <- sqrt( rinvgamma(p, 1, 1/Nu+Beta^2/(2*Tau^2*Sig^2)) )
Lam.pos[k,] <- Lam
# Nu
Nu <- rinvgamma(p, 1, 1+1/Lam^2)
# Tau
at.tau <- (p+1)/2
bt.tau <- 1/Xi + 0.5*sum(Beta^2/(Sig^2*Lam^2))
Tau <- sqrt( rinvgamma(1, at.tau, bt.tau) )
Tau.pos[k] <- Tau
# Xi
Xi <- rinvgamma(1, 1, 1+1/Tau^2)
}
## Summary
om <- 1:burn
Beta.pos <- Beta.pos[-om,]
Sig.pos <- Sig.pos[-om]
Tau.pos <- Tau.pos[-om]
Lam.pos <- Lam.pos[-om,]
Res <- list(beta=Beta.pos, sig=Sig.pos, tau=Tau.pos, lam=Lam.pos)
return(Res)
}
以下ではシミュレーションデータを使ってBayesian Lasso(ラプラス事前分布)と馬蹄事前分布の性能を比較してみます.
まず$n=100$, $p=20$として以下から擬似データを生成します.
y_i=\beta_0+\beta_1x_{i1}+\cdots+\beta_px_{ip}+\varepsilon_i, \ \ \ \ \varepsilon_i\sim N(0,\sigma^2)
ここで$(x_{i1},\ldots,x_{ip})$は平均$(0,\ldots,0)$, 分散共分散行列の$(j,k)$成分が$(0.5)^{|j-k|}$の多変量正規分布から生成します.また真のパラメータの値として$\beta_0=\beta_1=\beta_3=0.5,
\beta_2=-0.5, \beta_4=\cdots=\beta_p=0$, $\sigma=0.5$と設定します.
library(MASS)
set.seed(1)
n <- 100
p <- 20
Beta <- 0.5*c(1, -1, 1, rep(0, p-3))
mat <- matrix(NA, p, p)
for(k in 1:p){
for(j in 1:p){
mat[k,j] <- 0.5^(abs(k-j))
}
}
X <- mvrnorm(n, rep(0, p), mat)
Y <- 0.5 + as.vector(X%*%Beta) + 0.5*rnorm(n)
シミュレーションデータに対して上記のHS.Gibbs関数およびこちらの記事で作成したBL.GibbsとBR.Gibbsも比較のため適用します.
fit.HS <- HS.Gibbs(Y=Y, X=X, mc=3000, burn=1000) # Horseshoe
fit.BL <- BL.Gibbs(Y=Y, X=X, mc=3000, burn=1000) # Bayesian Lasso
fit.BR <- BR.Gibbs(Y=Y, X=X, mc=3000, burn=1000) # uniform prior
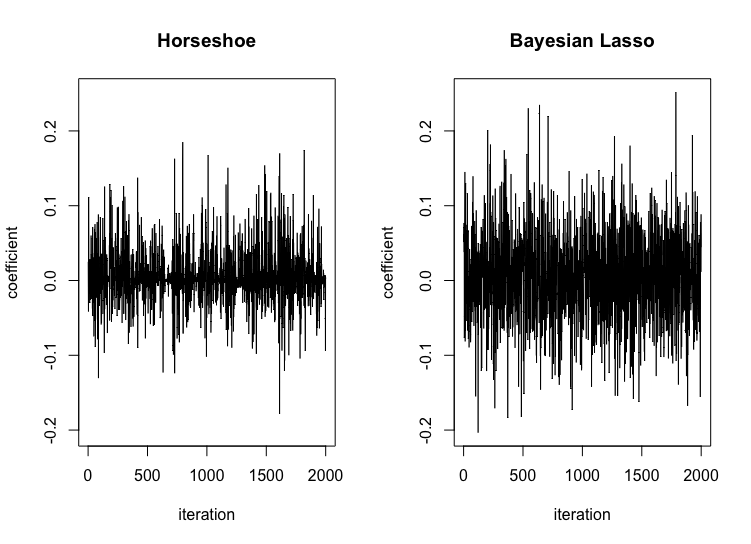
Bayesian Lassoと馬蹄事前分布の$\beta_{10}$の事後サンプルを比較してみます.
par(mfcol=c(1, 2))
ran <- range(fit.HS$beta[,10], fit.BL$beta[,10])
plot(fit.HS$beta[,10], type="l", ylab="coefficient", main="Horseshoe", xlab="iteration", ylim=ran)
plot(fit.BL$beta[,10], type="l", ylab="coefficient", main="Bayesian Lasso", xlab="iteration", ylim=ran)
$\beta_{10}$の真値は0ですが,馬蹄事前分布の方がBayesian Lassoと比べてより0付近に集中した事後サンプルが生成されていることがわかります.
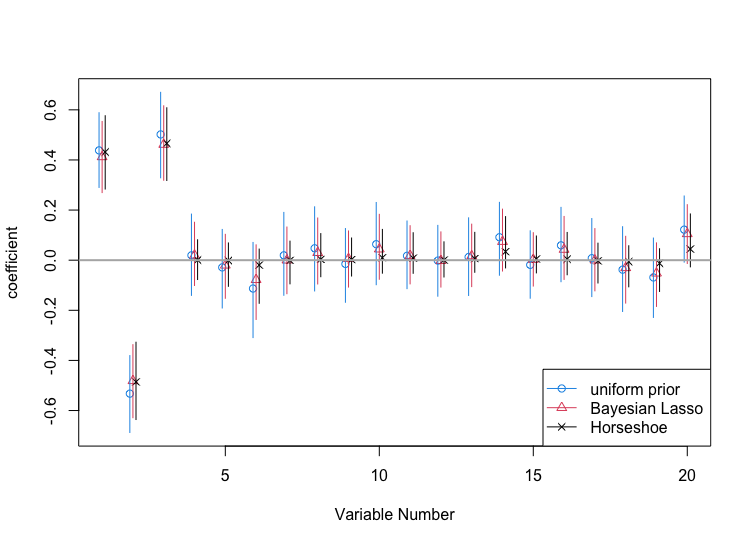
次に3つの事前分布によって得られた結果を点推定値と$95%$信用区間によって比較してみます.
PM.HS <- apply(fit.HS$beta, 2, median)[-1]
PM.BL <- apply(fit.BL$beta, 2, median)[-1]
PM.BR <- apply(fit.BR$beta, 2, median)[-1]
CI.HS <- apply(fit.HS$beta, 2, quantile, prob=c(0.025, 0.975))[,-1]
CI.BL <- apply(fit.BL$beta, 2, quantile, prob=c(0.025, 0.975))[,-1]
CI.BR <- apply(fit.BR$beta, 2, quantile, prob=c(0.025, 0.975))[,-1]
ran <- range(CI.BR, CI.HS, CI.BL)
p <- dim(X)[2]
bb <- seq(-0.1, 0.1, length=3)
pch <- c(1, 2, 4)
col <- c(4, 2, 1)
par(mfcol=c(1, 1))
plot(NA, xlim=c(1,p), ylim=ran, xlab="Variable Number", ylab="coefficient", main="")
points(cbind((1:p)+bb[1], PM.BR), ylim=ran, pch=pch[1], col=col[1])
points(cbind((1:p)+bb[2], PM.BL), ylim=ran, pch=pch[2], col=col[2])
points(cbind((1:p)+bb[3], PM.HS), ylim=ran, pch=pch[3], col=col[3])
for(k in 1:p){
lines(rep(k+bb[1],2), CI.BR[,k], col=col[1])
lines(rep(k+bb[2],2), CI.BL[,k], col=col[2])
lines(rep(k+bb[3],2), CI.HS[,k], col=col[3])
}
abline(h=0, lwd=2, col=grey(0.7))
legend("bottomright", legend=c("uniform prior", "Bayesian Lasso", "Horseshoe"), col=col, lty=c(1,1,1), pch=pch)
この結果から,真値が0の回帰係数に対して馬蹄事前分布による点推定値はBayesian Lassoと比べて0に近くなっており,馬蹄事前分布の強い縮小作用が確認できます.また,馬蹄事前分布は他の手法と比べて短い信用区間を与えており,効率的な事後推測ができていることもわかります.このように,馬蹄事前分布の推定値がほぼ0(または信用区間が0を含む)となっている変数をモデルから取り除くことで適切な変数選択ができることがわかります.
関連する話題
上記の数値例でも確認できたように,馬蹄事前分布は「0に近い値は強力に縮小する」性質を持っています.このような性質は回帰係数だけでなく様々な応用が考えられます.例えばFaulkner and Minin (2018)ではトレンド推定,Shin et al. (2020)ではノンパラメトリック回帰への応用が議論されています.
おわりに
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.