東京大学・株式会社Nospareの菅澤です.
こちらの記事でLassoのベイズ版であるBayesian Lassoのメカニズムについて紹介しました.今回はRのパッケージや自作関数を用いてBayesian Lassoを実際に使っていく方法を紹介していきたいと思います.
Diabetes data
今回はBayesian Lassoの元論文でも扱われているDiabetes data(糖尿病データ)を用いて進めていきます.このデータはlarsパッケージから利用可能です.
library(lars)
data(diabetes)
Y <- diabetes$y
X <- diabetes$x
このデータは442個のサンプル($n=442$)に対して10個の説明変数($p=10$)が与えられています.
Bayesian LassoのためのRパッケージ
Bayesian Lassoが実装されているRのパッケージはいくつかありますが,今回はBLRパッケージを使います.関数BLRを用いて以下のように簡単にBayesian Lassoを実行できます.
library(BLR)
bfit <- BLR(y=Y, XL=X, nIter=3000, burnIn=1000)
上のコードでnIterは全体のMCMCの長さ,burnInは収束前の期間(バーンイン期間)の長さを表しており,nIter - burnInの数だけ事後サンプルが得られます.出力として回帰係数の事後平均や事後標準誤差などが得られます.
フルスクラッチで実装してみる
前回の記事でギブスサンプリングを実行するために必要な完全条件付き分布の形を与えましたので,そこから繰り返しサンプルを生成する手順を実装することで,比較的簡単にBayesian Lassoの自作関数が作れます.以下でその一例を示します.
library(MCMCpack)
library(statmod)
BL.Gibbs <- function(Y, X, mc=2000, burn=500, lam.prior=c(1,1), sig.prior=c(1,1)){
## preparation
XX <- cbind(1, X)
n <- dim(XX)[1]
p <- dim(XX)[2]
a.lam <- lam.prior[1]
b.lam <- lam.prior[2]
a.sig <- sig.prior[1]
b.sig <- sig.prior[2]
## vectors/matrices to store posterior samples
Beta.pos <- matrix(NA, mc, p)
Sig.pos <- rep(NA, mc)
Lam.pos <- rep(NA, mc)
## initial values
init.fit <- lm(Y~X)
Beta <- coef(init.fit)
Sig <- summary(init.fit)$sigma
Lam <- 1
U <- rep(1, p) # latent variable
mat <- t(XX)%*%XX
## MCMC
for(k in 1:mc){
# Beta
invA <- solve( mat + diag(1/U) )
hbeta <- as.vector( invA%*%t(XX)%*%Y )
Beta <- mvrnorm(1, hbeta, Sig^2*invA)
Beta.pos[k,] <- Beta
# Sigma
resid <- as.vector( Y-XX%*%Beta )
Sig <- sqrt( rinvgamma(1, a.sig+0.5*(n+p-1), b.sig+0.5*sum(resid^2)+0.5*sum(Beta^2/U)) )
Sig.pos[k] <- Sig
# U
mu <- sqrt(Sig^2*Lam^2/Beta^2)
U <- 1/rinvgauss(p, mu, Lam^2)
# Lam
Lam <- sqrt( rgamma(1, a.lam+p, b.lam+0.5*sum(U)) )
Lam.pos[k] <- Lam
}
## Summary
om <- 1:burn
Beta.pos <- Beta.pos[-om,]
Sig.pos <- Sig.pos[-om]
Lam.pos <- Lam.pos[-om]
Res <- list(beta=Beta.pos, sig=Sig.pos, lam=Lam.pos)
return(Res)
}
上記の関数においてmcとburnはそれぞれ全体のMCMCの長さ,バーンイン期間の長さを表しています.結果としては,回帰係数(beta),誤差標準偏差(sig),罰則パラメータ(lam)の事後サンプルがリスト型のオブジェクトとして返ってくる形になっています.
上記の関数では逆ガンマ分布の乱数生成のためにMCMCpackパッケージ,逆ガウス分布からの乱数生成のためにstatmodパッケージを使用しています.
それではBL.GibbsをDiabetes dataに適用してみます.
fit.BL <- BL.Gibbs(Y=Y, X=X)
par(mfcol=c(2, 2))
plot(fit.BL$beta[,2], type="l", ylab="coefficient", xlab="iteration")
plot(fit.BL$beta[,3], type="l", ylab="coefficient", xlab="iteration")
plot(fit.BL$sig, type="l", ylab="sigma", xlab="iteration")
plot(fit.BL$lam, type="l",ylab="lambda", xlab="iteration")
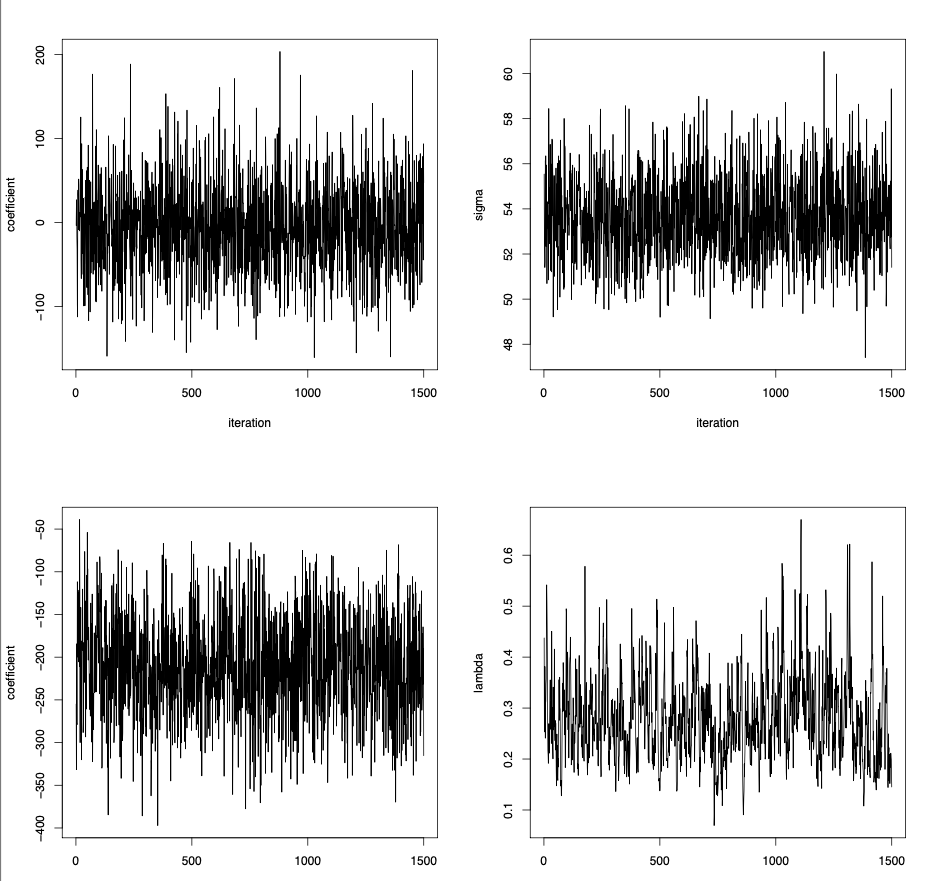
生成された事後分布のサンプルパス(左上:ageの回帰係数,左下:sexの回帰係数,右上:誤差標準偏差,右下:罰則パラメータ)は以下のようになり,うまく事後サンプルが生成できていそうなことがわかります.(厳密には収束判定などの数値的評価が必要です.)
また,BL.Gibbsで得られた事後サンプルから10個の回帰係数の事後平均を計算し,BLRの結果と比較してみます.
PM <- apply(fit.BL$beta, 2, mean)[-1]
bL <- bfit$bL # bfitはBLRの結果
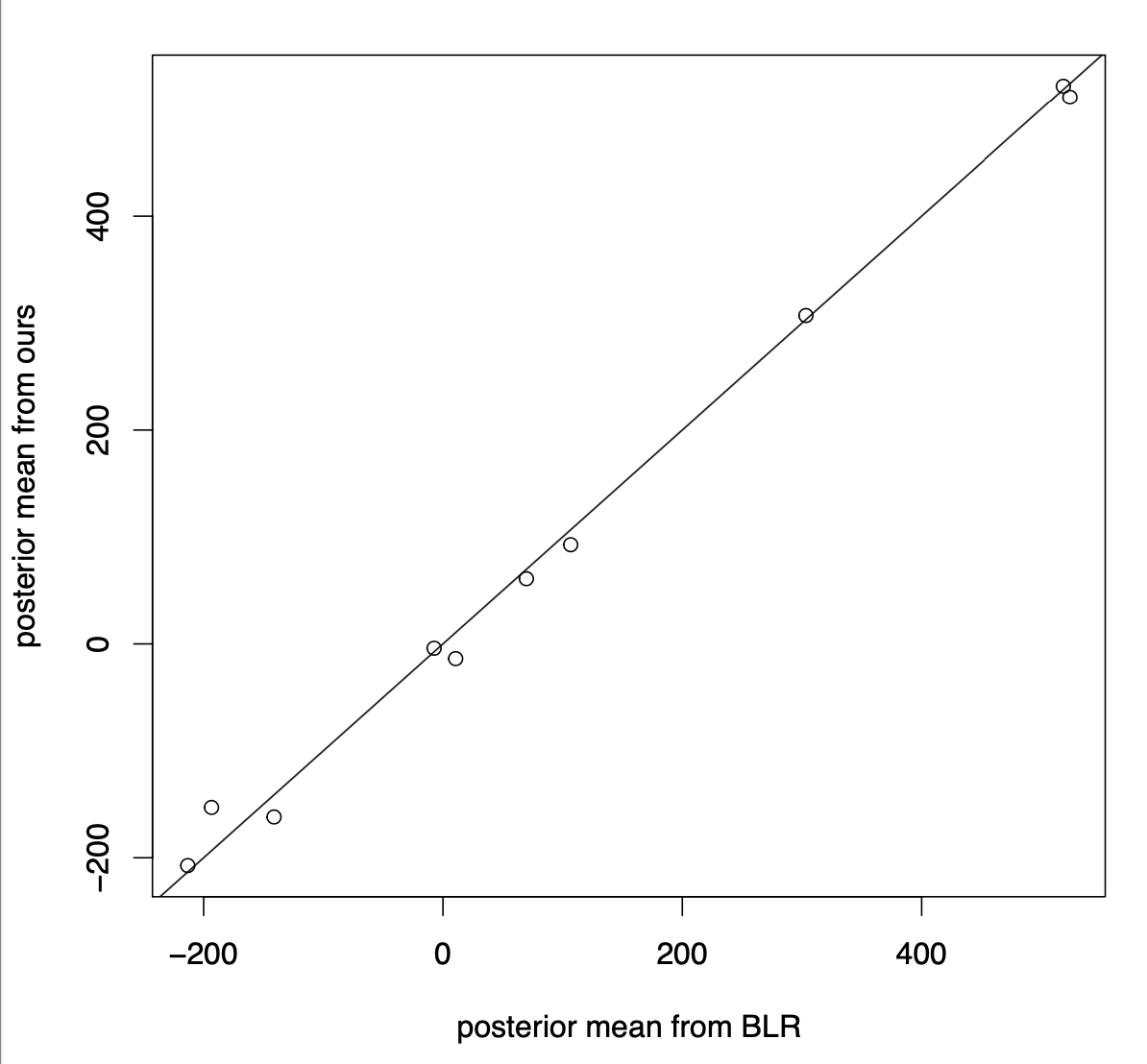
plot(bL, PM, xlab="posterior mean from BLR", ylab="posterior mean from ours")
abline(0, 1)
結果は以下のようになり,BLRパッケージによる結果と自作関数の結果がほぼ同じであることが確認できます.(同じ手法を実装しているので当たり前ですが.)
関連手法との比較
頻度論的なLassoおよび回帰係数にuniform prior(縮小事前分布でないもの)を用いた場合の結果と比較してみます.
まずはglmnetパッケージを用いて頻度論的なLassoを適用します.
set.seed(2)
library(glmnet)
opt.lam <- cv.glmnet(x=X, y=Y, nfold=10)$lambda.min
lfit <- glmnet(x=X, y=Y, lambda=opt.lam)
est.lasso <- coef(lfit)[-1]
est.lasso
ここではクロスバリデーションを用いて罰則パラメータの選択を行なっておりますが,乱数のシードを変えると結果がコロコロ変わってしまうのが難点です.(これはLassoの問題点というよりクロスバリデーションの問題点ですが...)
次に回帰係数に対してLaplace priorの代わりにuniform priorを用いることを考えます.これは通常の線形回帰の単純なベイズ版と捉えることができます.先ほどの自作関数を少し改変してuniform prior用の関数を作っておきます.
BR.Gibbs <- function(Y, X, mc=2000, burn=500, sig.prior=c(1,1)){
## preparation
XX <- cbind(1, X)
n <- dim(XX)[1]
p <- dim(XX)[2]
a.sig <- sig.prior[1]
b.sig <- sig.prior[2]
## vectors/matrices to store posterior samples
Beta.pos <- matrix(NA, mc, p)
Sig.pos <- rep(NA, mc)
## initial values
init.fit <- lm(Y~X)
Beta <- coef(init.fit)
Sig <- summary(init.fit)$sigma
invA <- solve(t(XX)%*%XX)
## MCMC
for(k in 1:mc){
# Beta
hbeta <- as.vector( invA%*%t(XX)%*%Y )
Beta <- mvrnorm(1, hbeta, Sig^2*invA)
Beta.pos[k,] <- Beta
# Sigma
resid <- as.vector( Y-XX%*%Beta )
Sig <- sqrt( rinvgamma(1, a.sig+0.5*n, b.sig+0.5*sum(resid^2)) )
Sig.pos[k] <- Sig
}
## Summary
om <- 1:burn
Beta.pos <- Beta.pos[-om,]
Sig.pos <- Sig.pos[-om]
Res <- list(beta=Beta.pos, sig=Sig.pos)
return(Res)
}
この関数をDiabetes dataに適用します.
fit.BR <- BR.Gibbs(Y=Y, X=X)
PM.BR <- apply(fit.BR$beta, 2, median)[-1] # 事後中央値
CI.BR <- apply(fit.BR$beta, 2, quantile, prob=c(0.025, 0.975))[,-1] # 95%信用区間
同じような要約量をBL.Gibbs(Bayesian Lassoの自作関数)の出力から計算します.
PM.BL <- apply(fit.BL$beta, 2, median)[-1] # 事後中央値
CI.BL <- apply(fit.BL$beta, 2, quantile, prob=c(0.025, 0.975))[,-1] # 95%信用区間
3つの手法の結果を図示します.
ran <- range(CI.BL, CI.BR)
p <- dim(X)[2]
bb <- seq(-0.1, 0.1, length=3)
pch <- c(1, 2, 4)
col <- c(4, 2, 1)
plot(NA, xlim=c(1,p), ylim=ran, xlab="Variable Number", ylab="coefficient", main="")
points(cbind((1:p)+bb[1], PM.BR), ylim=ran, pch=pch[1], col=col[1])
points(cbind((1:p)+bb[2], PM.BL), ylim=ran, pch=pch[2], col=col[2])
points(cbind((1:p)+bb[3], est.lasso), ylim=ran, pch=pch[3], col=col[3])
for(k in 1:p){
lines(rep(k+bb[1],2), CI.BR[,k], col=col[1])
lines(rep(k+bb[2],2), CI.BL[,k], col=col[2])
}
abline(h=0, lwd=2)
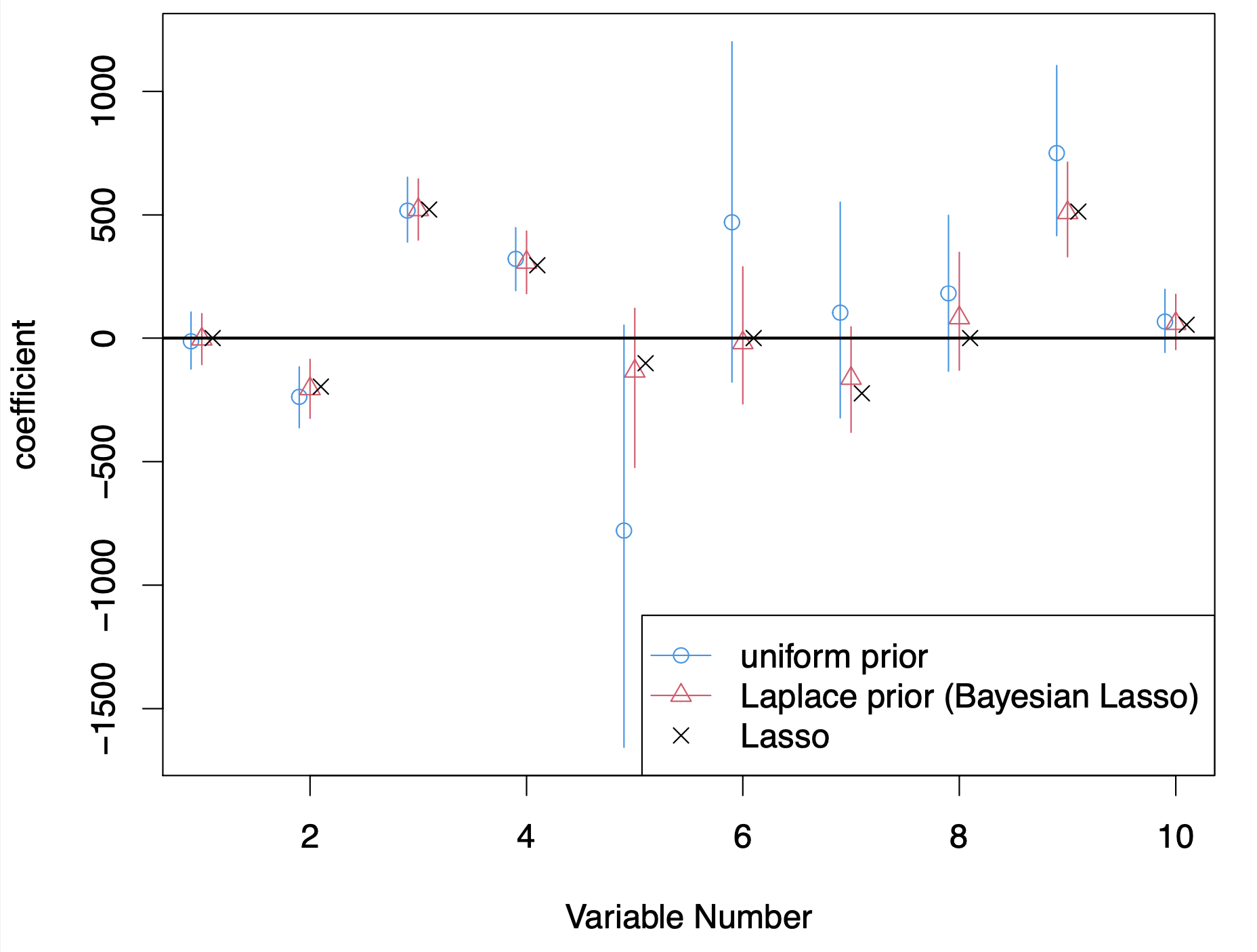
legend("bottomright", legend=c("uniform prior", "Laplace prior (Bayesian Lasso)", "Lasso"), col=col, lty=c(1,1,NA), pch=pch)
上記の結果から以下のことが観察できます.
-
Bayesian Lassoの事後中央値は頻度論的なLassoの推定値と近い値になっている.一方で,頻度論的なLassoと異なり,Bayesian Lassoの中央値はexactに0とはならない.
-
uniform priorとLaplace prior(Bayesian Lasso)の結果を比べると,後者の方は0への縮小効果を持ち,その結果として信用区間の長さが大幅に短くなっている.
前回紹介したように,Bayesian LassoのMAP推定値は頻度論のLassoの推定値と一致するのですが,MCMCの出力からMAPを推定するのは困難です.そこで事後中央値などMCMCの出力から簡単に計算できる量を使うことになるのですが,その結果「推定値がexactに0になる」性質は失われてしまいます.これは確かに欠点ではあるのですが,その代わりに信用区間を簡単に計算できる恩恵を受けられるのがBayesian Lassoの特徴です.
最後に
今回はBayesian LassoのRでの実装について紹介しました.比較の図から観察できたように,Bayesian Lassoでは点推定値がexactに0にならず,場合によっては若干中途半端な(0に近いけど0じゃない)推定値が出力される可能性があります.これをベイズ的に解決するには**「不必要な回帰係数に対してより強力な縮小作用を持つ事前分布」**が必要になります.
このような性質を持つ代表的な事前分布としてhorseshoe prior(馬蹄事前分布)があります.Bayesian Lassoに関する知識を持っていれば比較的容易に理解することができますので,詳しくは次の記事で紹介します.
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.