東京大学・株式会社Nospareの菅澤です.
こちらの記事でLassoのベイズ版であるBayesian Lassoのメカニズムについて紹介し,こちらの記事ではRでの実装について扱いました.
頻度論的なLassoと比べて,Bayesian Lassoの事後中央値はexactに0の値とならないことが欠点として挙げられていました.(その代わりに推定結果の不確実性評価が容易に実行できることが利点です.)
そこで,今回はBayesian Lassoの発展版である**Horseshoe prior(馬蹄事前分布)**について紹介します.
単純な設定(シグナル推定)における議論
Horseshoe priorのコンセプトを明確化するために,まずかなり単純化した以下のモデルで議論します.
y_i=\beta_i+\varepsilon_i, \ \ \ \varepsilon_i\sim N(0, 1), \ \ \ \ i=1,\ldots,n.
上のモデルでは$i$ごとの独立性を仮定しています.
このモデルは,$\beta_i$が真のシグナル,$y_i$はノイズが乗ったシグナルとして,$y_i$のノイズ除去(denoising)を行うモデルとして用いられます.
変数選択の際と同様に,$\beta_i$の多くの成分は0であること(スパース性)を想定します.今,$\beta_i$に対する事前分布として,以下のような正規分布のスケール混合のクラスを考えます.
(\beta_i \ |\ \lambda_i,\tau) \sim N(0, \lambda_i^2\tau^2), \ \ \ \ \ \ \ \lambda_i\sim \pi(\cdot), \ \ \ \ \ \
i=1,\ldots,n.
このモデルにおけるBayesian Lassoは$\beta_i$に対してラプラス分布を仮定することに相当しますが,それは上の混合表現において$\lambda_i^2\sim {\rm Exp}(2)$を考えることに相当します.
この枠組みにおいて,$\lambda_i$に対してどのような分布を使うのが好ましいか($\lambda_i^2\sim {\rm Exp}(2)$で良いのか)について考えていきます.
事後平均と縮小係数
$\lambda_i$の分布について議論していくために,$\beta_i$の事後平均を考えます.
以下では簡単のために$\tau=1$を仮定します.
$\lambda_i$が所与のもとで$\beta_i$の事後分布は正規分布になるので,(条件付き)事後平均は以下のような簡単な形で求めることができます.
E(\beta_i \ | \ y_i,\lambda_i^2)=\frac{\lambda_i^2}{1+\lambda_i^2}y_i \equiv (1-\kappa_i)y_i, \ \ \ \ \ \ \ \kappa_i=\frac{1}{1+\lambda_i^2}.
ここで$\kappa_i\in(0,1)$は縮小係数と呼ばれる量で,観測されたシグナル$y_i$を原点方向にどの程度縮小するかをコントロールしていることがわかります.
極端な状況としては以下の2つの場合です.
- ($\kappa_i=1$のとき) $y_i$を完全に0に縮小する.($\beta_i$を0と推定する.)
- ($\kappa_i=0$のとき) $y_i$を全く縮小しない. ($y_i$をそのまま$\beta_i$の推定に用いる.)
また,$\beta_i$の周辺事後平均は
E(\beta_i \ | \ y_i)=\int_{0}^1(1-\kappa_i)y_i\pi(\kappa_i|y_i)d\kappa_i
=\big(1-E[\kappa_i|y_i]\big)y_i.
となり,$\lambda_i$そのものではなく,それを変換した(パラメータ変換をした)$\kappa_i$の事後分布が,$\beta_i$の事後平均を考える上で重要であることがわかります.
「Horseshoe(馬蹄)」の由来
これまでの議論から$\lambda_i$よりも$\kappa_i$の事後分布の方が$\beta_i$の推定に直接的に重要であることがわかりましたので,$\kappa_i$に対する事前分布の議論を経由して$\lambda_i$に対する事前分布を議論していきましょう.
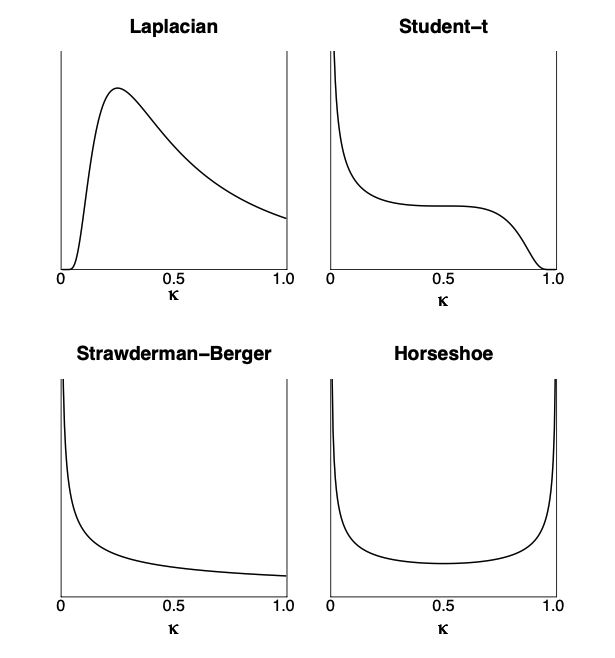
以下の図は Carvalho et al. (2009, AISTAT) に掲載されている図で,いくつかの$\lambda_i$の分布に対応した$\kappa_i$の事前分布の密度関数が図示されています.
左上のLaplacianがLaplace分布(すなわち$\lambda_i^2\sim {\rm Exp}(2)$)のケースに相当します.
右上および左下の事前分布も代表的なものとして知られていますが,今回の記事では深く触れないことにします.
Laplace分布が与える$\kappa_i$の事前分布のポイントは以下の2点です.
- $\kappa_i=0$付近に密度がほとんどない.
- $\kappa_i=1$の密度関数の値が有限な正の値になっている.
1は事後分布においても$\kappa=0$付近の値を取る可能性がほとんどないことを意味しています.すなわち,$\beta_i$の事後平均において任意のシグナル$y_i$は常にある程度縮小されてしまうことを意味しています.これは過剰縮小の問題として知られてまして,(ちょっと飛躍しますが)線形回帰モデルの文脈では,真の回帰係数の絶対値が大きい場合も事後平均において縮小されてしまって効果を過小評価していることに相当します.
一方で,2はスパース性に関連する性質で,$\kappa_i=1$に事前分布の段階である程度の重みを置いている($\beta_i$がスパースになることを事前に想定している)ことを意味しますので,これまでに紹介したBayesian Lassoの性質が$\kappa_i$の観点で見ても確認できることがわかります.
さて,これまでの議論が理解できれば,$\kappa_i$のスケールでより自然な事前分布が導入できることがわかります.
- 過剰縮小を避けるために$\kappa_i=0$周辺に密度を集中させたい.
- スパースな推定を行うために$\kappa_i=1$周辺に密度を集中させたい.
の要請を満たす自然な分布形が図の右下にHorseshoeとして与えられています.
まさに,この**$\kappa_i$の密度関数の形状がHorseshoe(馬蹄)に似ていることからHorseshoe prior(馬蹄事前分布)と呼ばれています**.
Horseshoe priorの具体的な形
$\kappa_i$のスケールにおける密度関数の具体的な関数形は$\kappa_i\sim {\rm Beta}(1/2, 1/2)$です.
また,これを元々の$\lambda_i$のスケールに戻すと以下のような分布が得られます.
\pi(\lambda_i)=\frac{2}{\pi}\frac{1}{1+\lambda_i^2}, \ \ \ \ \lambda_i>0 \ \ \ \ \
\Leftrightarrow \ \ \ \ \
\pi(\kappa_i)=\frac{1}{\pi}\kappa_i^{-1/2}(1-\kappa_i)^{-1/2}, \ \ \ \ \kappa_i\in (0,1).
$\lambda_i$の密度関数形は(標準)Half-Cauchy分布として知られており,$C^{+}(0,1)$と表します.
余談
勘が良い人は「$\kappa_i=0$と$\kappa_i=1$に密度を集中させたいなら$\kappa_i=0, 1$上の2点分布を使っちゃえばいいんじゃないの?」と思うかもしれません.
実はこのような事前分布はSpike-and-Slab priorとして知られているものです.
しかし,Spike-and-Slab priorを使った際は事後分布の計算コストが(特に線形回帰モデルの枠組みで)非常に高いことが知られています.端的な理由としては,$\beta_i$の周辺分布が有限混合モデルになるからです.一方で,$\kappa_i$に対して連続な分布を用いれば,Spike-and-Slab priorよりもはるかに計算コストが抑えられることがわかっています.この観点で見ると,Horseshoer priorは形的にSpike-and-Slab priorを連続関数で近似しているものであると捉えることもできます.
線形回帰モデルにおけるHorseshoe prior
線形回帰モデルにおけるHorseshoe priorについてまとめておきます.基本的にはシグナル推定で構成した事前分布を回帰係数の事前分布に用いるだけです.
線形回帰モデル
y=X\beta + \varepsilon, \ \ \ \ \ \varepsilon\sim N(0, \sigma^2I_n)
において,$\beta=(\beta_1,\ldots,\beta_p)^{\top}$の各要素に対するHorseshoe priorは
\beta_k \ | \ \lambda_k\sim N(0, \lambda_k^2\tau^2\sigma^2), \ \ \ \ \lambda_k\sim C^{+}(0,1), \ \ \ \ k=1,\ldots,p
で与えられます.
上記において$\lambda_k$を局所縮小パラメータ(local shrinkage parameter),$\tau^2$を大域縮小パラメータ(global shrinkage parameter)と呼ばれることが多いです.
それは$\lambda_k$および$\tau^2$がそれぞれ個々の説明変数の(局所的な)効果の縮小と全体的な係数推定の縮小をコントロールしているパラメータと解釈できるからです.
Horseshoe priorの注意点としては,$\lambda_k$を周辺化した$\beta_k$の周辺事前分布が解析的に求まらないことです. すなわち,Laplace priorと異なり,Horseshoe priorは回帰係数の罰則付き目的関数として見たときに罰則項がどのような形になっているかは自明ではないということになります.これは,Bayesian Lassoとは異なり,Horseshoe priorが頻度論的な議論からだけでは生まれにくい,まさにベイズ的な観点で生まれた縮小事前分布であると言えます.
また,実用上非常に重要な点として,$\beta_k$の周辺事前分布は解析的に求まらなくても,$\beta_k$の事後分布の計算(近似)はギブスサンプリングによるMCMCで容易に実行することができます.
この詳細についてはRでの実装も含め次回紹介していこうと思います.
おわりに
Horseshoe priorについてより詳しく勉強したい方は本文でも引用した Carvalho et al. (2009, AISTAT) やCarvalho et al. (2010, Biometrika)を参照してください.(どちらもオープンアクセスです.)
また高次元におけるHorseshoeの理論的な性質についてはBhadra et al. (2019, Statistical Science)に包括的にまとまっています.
株式会社Nospareでは統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.