こんにちは、高校 3 年生の square1001 です。
私が好きな競技プログラミングでは、AtCoder や TopCoder のコンテストに出場したり、情報オリンピックの日本代表選手に選ばれたりしています。TopCoder のアルゴリズム部門では「レッドコーダー」で、2020 年 6 月時点での世界ランクは 35 位です。また、読者の中で AtCoder に参加している人は、コンテスト作成者として見かけることもあるかと思います。
本記事では、大きな数の計算について書いていきます。一部の章では C++ での実装例を紹介していますが、読者が使うプログラミング言語に関係なく読める内容になっているでしょう。
【シリーズ】
- 前編:大きな数の四則計算を圧倒的な速度で! ← 本記事
- 後編:N! の計算から円周率 100 万桁の挑戦まで
0. はじめに
ところでみなさん、「大きな数の計算」に関連した興味を持ったことはありますか?例えば…
- $2$ の $1000$ 乗っていくつ?正確な値を計算してみたい!
- $N$ 桁 $\times$ $N$ 桁の掛け算は、$N^{2}$ 回よりも少ない計算回数でできるの?
- 円周率 $\pi = 3.141592...$ を、小数点以下何万桁もどうやって計算できるの?
こういう人も多いかと思いましたが、分かりやすく書かれている記事が見つからず、難しそうだな、と思った人もいるかもしれません。私だってそうでした。でも知った瞬間には、めっちゃ面白い!と思って、もう感動です。
この理由もあって、2018 年 12 月に開催されたパ研合宿(筑駒パソコン研究部と開成コンピューター部が共同で行った合宿)で、円周率 100 万桁の計算をゴールに、講演をしました。この講演には、中学 1 年の部員も多く参加していました。これでも、アルゴリズムの内容とその面白さが伝わって、メッチャうれしかったのを覚えています。
あれから 1 年半、今回は分かりやすくまとめる目的もあって Qiita に記事を書いてみました。面白い事実がたくさん隠されているので、ぜひこの記事を読んでほしいなと思っています。
多倍長整数演算とは?
本記事のタイトルにある「多倍長整数演算」とは何でしょう。
これは、普通にコードを書くと計算できないような大きな数を計算することをいいます。例えば、C++ の場合「long long 整数型」を使っても $2^{63}$、つまりおよそ $9 \times 10^{18}$ までしか計算できませんが、
なんと工夫すればそれが計算出来てしまうのです!!!
それだけでなく、Python など一部の言語にサポートされている「大きな数の計算ができるライブラリ(機能)」より速く計算出来てしまうアルゴリズムがあるのです。
本記事では、それについて分かりやすく、そして深く解説したいと思います。
本記事の構成について
本記事は、以下の 4 章構成になっています。自分のレベルと興味に合わせて読んでください。
第 1 章:はじめに ~メインを読むための準備~
| 章 | タイトル | 備考 |
|---|---|---|
| 1-1. | 人間の計算速度はどのくらい? | |
| 1-2. | コンピューターの計算速度はどのくらい? | |
| 1-3. | 計算回数をかぞえてみよう | 計算時間について扱います |
第 2 章:多倍長整数演算 ~初級編~
| 章 | タイトル | 備考 |
|---|---|---|
| 2-1. | プログラミングでも大きな数を扱いたい! | 大きな数の実装、スタート! |
| 2-2. | 大きな数の足し算 | |
| 2-3. | 大きな数の引き算 | |
| 2-4. | 繰り上がり処理 | 単純な実装には欠かせない! |
| 2-5. | 大きな数の掛け算 | |
| 2-6. | 大きな数の割り算 | |
| 2-7. | ここまでのまとめ |
第 3 章:多倍長整数演算 ~理論編~
| 章 | タイトル | 備考 |
|---|---|---|
| 3-1. | 1960 年 ~すべての始まり~ | |
| 3-2. | 画期的な掛け算の方法、カラツバ法! | 意外とシンプルです |
| 3-3. | さらに速い、Toom-Cook 法! | |
| 3-4. | 現在最速!FFT 掛け算 | 計算時間 O(N × log(N)) |
| 3-5. | ニュートン=ラフソンの割り算アルゴリズム | 計算時間 O(N × log(N)) |
| 3-6. | ゴールドシュミットの割り算アルゴリズム | O(N × log²(N)) だけど手軽! |
| 3-7. | ここまでのまとめ |
第 4 章:多倍長整数演算 ~応用編~
| 章 | タイトル | 備考 |
|---|---|---|
| 4-1. | N! の高速な計算 | 感動的なアルゴリズムかも? |
| 4-2. | √2 を精度よく求めよう | ここにもニュートン法が登場! |
| 4-3. | 円周率 100 万桁に挑戦! | |
| 4-4. | Constants コンテストへのいざない | |
| 4-5. | 大きな数を使った面白い問題の紹介 | |
| 5. | おわりに |
1. はじめに ~メインを読むための準備~
まず、大きな数の計算の話をする前に、少しコンピューターと計算回数について話しましょうか。
コンピューターは、現代ではソフトウェアやアプリケーションの開発に使われていますが、これには重要な背景があります。これは「計算がめっちゃ速いこと」です!人間なんかと比べたら、圧倒的な計算スピードを誇ります。
1-1. 人間の計算速度はどのくらい?
まず人間はどのくらいの速度で計算できるでしょうか?速い人も遅い人もいると思います。
例えば、$628 \times 463$ の計算を、今やってみましょう。10 秒以内で計算できたらかなり速い方でしょう。この計算では、次のように「単純計算」を合計 28 回もしていることになります。
- 9 回の 1 桁 × 1 桁の掛け算
- 6 回の 1 桁 × 1 桁の足し算
- 13 回の繰り上がり計算
もし $628 × 463$ が 10 秒で計算できたならば、1 秒間に 2.8 回のペースで単純計算ができていることになります。そう言われてみれば、かなり速いように感じるかもしれません。中には、そろばんに慣れている読者とかで、「一秒間に 10 回計算できる!」という人もいると思います。
世界ではフランスの アレクシス・ルメール さんが、**「100 桁の数の 13 乗根を 3.625 秒で計算した」**という世界記録を持っています。しかし、これでも計算速度は 1 秒につき 1,000 回程度にしかならないでしょう。
(https://www.theepochtimes.com/survey-1-out-of-5-adults-have-forgotten-how-to-do-fractions-or-percentages_1986839.html)
1-2. コンピューターの計算速度はどのくらい?
一般的なコンピューターでも、1 秒に 10 億回くらい計算ができる、と言われています。これは最も計算が早い人間よりも 100 万倍くらい速い、ということです。
また、つい最近に使われ始めたスーパーコンピューター「富岳」は 1 秒に 40 京回 ($4 \times 10^{17}$ 回) も計算できることが知られています。つまり、コンピューターはめっちゃ早く計算できる!ということです。
しかし、コンピューターの計算速度にも限界というものはあります。例えば、現代のコンピューターをしても、200 桁の数の素因数分解でさえ、非常に難しいとされています。
1-3. 計算回数をかぞえてみよう
例えば、$N$ 桁 $\times$ $N$ 桁の掛け算は、下の図のように筆算すると、どのくらいの計算回数を必要とするでしょうか?

答えは、以下の通りになります。
- オレンジの部分で、$N$ 桁 $\times$ $1$ 桁の掛け算を $N$ 回やっているから、$N^{2}$ 回くらいの掛け算と、$N^{2}$ 回以下の繰り上がり計算をしている。
- 赤の部分で、合計して $N^{2}$ 個くらいの数の足し算をしている。
ですから、計算回数は $3 \times N^{2}$ 回くらい、ということになるでしょう。1 秒に 10 億回くらいの計算ができる一般的なコンピューターで 1 万桁の掛け算の筆算をすると、1 秒以内で計算が終わることが想像できるでしょう。それに対して、100 万桁の掛け算の筆算をすると、コンピューターでも数時間かかることが分かります。とても長い時間がかかってしまうのです!
掛け算の筆算のプログラムの計算時間は $O(N^{2})$ です。このオーダー表記では「×3」などといった定数倍は、すべて無視します。すると、大まかな計算回数が見積もりやすいです。
「計算時間 (計算量オーダー) についてもっと知りたい!」という人は、こちらの記事も読みましょう。めっちゃ分かりやすいです。
実はもっと高速な方法がある
しかし、世の中には筆算の $O(N^{2})$ よりも速い計算時間で掛け算する方法が、実はあるんです。
これは意外と最近、1960 年にアナトリー・カラツバさんが発見した「カラツバ法」で、N 桁の掛け算を計算時間 $O(N^{1.59})$ でできます。天才的ですが、意外とシンプルな方法です。
現在知られている一番高速な掛け算のアルゴリズムの計算時間は $O(N \times \log N)$ です。単純に $N$ の値を当てはめて計算すると、$N = 2^{20}$ (およそ 100 万桁) でも計算回数が $20 \times 2^{20}$ 回です。実際は定数倍として、この数倍は計算回数が必要ですが、これでも 1 秒以内で計算できることを意味します。
なんか凄いですよね?
このなんかやばそうな掛け算のアルゴリズムは、第 3 章で説明することにするので、楽しみにしておいてください。
2. 多倍長整数演算 ~初級編~
ここから実際に、大きな数の計算に入っていきます!
第 2 章では、まず最初にプログラミングで大きな数をどうやって扱うのかを説明し、この上で大きな数の正確な足し算・引き算・掛け算・割り算を実現する方法を紹介します。
プログラミングの世界では、大きな整数の計算は**「多倍長整数演算」**とも呼ばれます。
多倍長整数演算は、普通の 32 ビットの整数型 (C++ や Java でいう「int 型」) や、浮動小数点数型 (C++ や Java でいう「double 型」) では扱えず、その代わりに 1 桁ごとのデータから計算するプログラムを実装して計算します。
本章では C++ での実装例も紹介しますが、「どんな方法を使って計算するのか?」(これをアルゴリズムといいます) の理解の補助的な役割として見るとよいでしょう。それさえ分かれば、使うプログラミング言語にかかわらず、実装できるでしょう!
2-1. プログラミングでも大きな数を扱いたい!
本節では、大きな数をどうやって管理するのか、計算の前段階を説明します。
2-1-1. しかし、普通には計算できない!
プログラミングで大きな数を計算したい!と思ったプログラマーは多いと思います。でも、普通の計算ではうまくいきません。
例えば、次の C++ のプログラムを動作してみましょう。
int x = 1234567890, y = 2005272115;
cout << x + y << endl; // <----「x + y の値を表示する!」という意味
答えは「3239840005」のはずです。しかし実行してみると、おそらく次のように表示されるでしょう。
-1055127291
明らかにおかしい値が表示されています。どうしてこんなことに!
なぜなら、「オーバーフロー」が起こっているからです。C++ や Java などでは、「int 型」は 32 ビットの整数型です。これは 32 桁の 2 進数のことです。つまり、
- int 型では、$-2^{31}$ 以上 $2^{31}-1$ 以下の数しか表せません
- この範囲は、-2,147,483,648 ~ 2,147,483,647 にあたります
- 計算結果がこの範囲を超えてしまうと「オーバーフロー」が起こります
参考程度に、C++ には「long long 型」もありますが、64 ビットなので $2^{63}$ 以上の数を扱うことができません。また小数を表せる double 型も 64 ビットなので、ある程度の大きな数になると誤差が出て、正確な値が計算できません。例えば、エクセルに $2^{100}$ を計算させて、下の 16 桁が全部 0 でおかしいなと思った人もいると思います。
つまり、どうすればいいのか?
$2^{63}$ 以上の大きな数を扱うためには、次のような方法が考えられます。
- Java や Python など、無限に大きな数を扱えるプログラミング言語を使う
- 自分で大きな数の計算のアルゴリズムを理解し、これを実装する
Java や Python を使える人にとっては、確かに 2, 3 章を読み飛ばしてよい!と思うかもしれませんが、どんな感じの方法で動いてるのか中身を知りたい!とか、標準ライブラリに頼らずに自分で実装したい!とかあるでしょう。
特に 3 章の内容は、知らない読者がほとんどだと思います。マジで面白いです。また、例えば Python の整数の型では、掛け算は計算時間 $O(N^{1.59})$、割り算は計算時間 $O(N^2)$ のアルゴリズムで実装されていますが、両方ともさらに高速なアルゴリズムがあります。
2-1-2. 大きな数はどうやって管理する?
だったら、大きな数はどうやって計算するのでしょうか?人間なら、例えば「14348907」は 8 つの数字からなる文字列として見ているでしょう。実装方法の例として、次の方法が考えられます。
| 方法 | 例 |
|---|---|
| N 桁の数を、長さ N の文字列として管理する | 14348907 → "14348907" |
| N 桁の数を、長さ N の配列として管理する |
14348907 → {7, 0, 9, 8, 4, 3, 4, 1}(詳しくは後述) |
どちらにせよ、1 桁ごとの数字の列として管理しなければならない、ということです!
本記事では主に 0 以上の整数の計算について扱います。負の数を使いたいなら、これとは別に「マイナスがついているか」の true/false の値と合わせて管理する必要があります。
$N$ 桁の数を、長さ $N$ の配列として管理する方法で実装例を説明します。$N$ 桁の整数 $A$ を、配列 $a = (a_0, a_1, a_2, ..., a_{N-1})$ を使って
$$A = a_0 + a_1 \times 10 + a_2 \times 100 + \cdots + a_{N-1} \times 10^{N-1}$$
と表すということです!実際の数の書き方と逆順になっています。
例えば、配列 digit = { 6, 1, 2, 7, 7, 7, 6, 1 } は、16777216 という整数を表しています。
大きな数を入力しよう!
C++ などのプログラミング言語の場合は、入力は文字列として受け取って、下のような配列に変換する関数を作ってこれを呼び出すようにすると、実装しやすいです。
vector<int> string_to_bigint(string S) {
int N = S.size(); // N = (文字列 S の長さ)
vector<int> digit(N);
for(int i = 0; i < N; ++i) {
digit[i] = S[N - i - 1] - '0'; // 10^i の位の数
}
return digit;
}
大きな数を表示しよう!
同じように、大きな数の表示は、下のように文字列に変換する関数を作ってやり、これを呼び出して表示する方法が、実装しやすいでしょう。
string bigint_to_string(vector<int> digit) {
int N = digit.size(); // N = (配列 digit の長さ)
string str = "";
for(int i = N - 1; i >= 0; --i) {
str += digit[i] + '0';
}
return str;
}
2-2. 大きな数の足し算
みなさんは小学 3 年生くらいで、大きな数の足し算を習ったと思います。この時を思い出して、筆算に似たアルゴリズムを使って、配列で表された大きな 2 つの数の足し算をしましょう!
例 1:「1524 + 2061」の計算
例えば、$1524 + 2061$ を、桁ごとの配列で表したまま計算すると…?
- $(4, 2, 5, 1)$ と $(1, 6, 0, 2)$ を足し合わせて $(5, 8, 5, 3)$ だから、答えは「3585」
基本的には、それぞれ足し合わせてもよさそうに見えますね…
例 2:「4623 + 2381」の計算
しかし、例えば $4623 + 2381$ の計算などで失敗します。
- $(3, 2, 6, 4)$ と $(1, 8, 3, 2)$ を足し合わせて $(4, 10, 9, 6)$ だから、答えは「69104」???
そう、繰り上がりがあるからです!それぞれの桁の数字は、0 以上 9 以下になるはずだから、10 以上になったところは繰り上がりをして 9 以下にする必要が出てきます。先ほどの例だと:
- まず、(4, 10, 9, 6) の 10 の位を繰り上げて、(4, 0, 10, 6) にする!
- 次に、(4, 0, 10, 6)の 100 の位を繰り上げて、(4, 0, 0, 7) にする!
- これで、4623 + 2381 = 7004 が求まった!
足し算を実装してみよう!
配列 $(4, 10, 9, 6)$ を $(4, 0, 0, 7)$ にするように、配列を「繰り上げる」プログラムができれば、配列を足し合わせるだけなので、簡単に実装できそうですね?
※関数 carry_and_fix は、2-4 節「繰り上がり処理」で出てきます。
vector<int> addition(vector<int> digit_a, vector<int> digit_b) {
int N = max(digit_a.size(), digit_b.size()); // a と b の大きい方
vector<int> digit_ans(N); // 長さ N の配列 digit_ans を作る
for(int i = 0; i < N; ++i) {
digit_ans[i] = (i < digit_a.size() ? digit_a[i] : 0) + (i < digit_b.size() ? digit_b[i] : 0);
// digit_ans[i] を digit_a[i] + digit_b[i] にする (範囲外の場合は 0)
}
return carry_and_fix(digit_ans); // 2-4 節「繰り上がり計算」の関数です
}
繰り上がりも最大 $N$ 回しかなさそうです。だから、足し算の計算時間は $O(N)$ です!
繰り上がりの関数を作りさえすれば、魔法のように一瞬です。
2-3. 大きな数の引き算
足し算と同じように、これも筆算ベースで行うことができます。小学生の頃に大きな数の足し算や引き算をしたと思いますが、繰り上がりと繰り下がりがちょっと違うけど似てるなあと思った人もいるでしょう。2 つの例で説明してみます。
例 1:「3859 - 1414」の計算
配列 $(9, 5, 8, 3)$ から配列 $(4, 1, 4, 1)$ を引くと、$(5, 4, 4, 2)$ になるので、答えは「2445」
例 2:「9630 - 5248」の計算
配列 $(0, 3, 6, 9)$ から配列 $(8, 4, 2, 5)$ を引くと、$(-8, -1, 4, 4)$ になる。ここで:
- (-8, -1, 4, 4) の 1 の位を繰り下げて、(2, -2, 4, 4) にする
- (2, -2, 4, 4) の 1 の位を繰り下げて、(2, 8, 3, 4) にする
- これで 9630 - 5248 = 4382 が求まった!!!
引き算を実装してみよう!
配列 $(-8, -1, 4, 4)$ を $(2, 8, 3, 4)$ にするように、配列を「繰り下げる」プログラムができれば、配列のそれぞれの値を引き算するだけなので、簡単に実装できそうですね?これは
で実装例として書く、繰り下がりをする関数「carry_and_fix」です。これを使えば、次のように超シンプルに大きな数の引き算ができます!!!
vector<int> subtraction(vector<int> digit_a, vector<int> digit_b) {
int N = max(digit_a.size(), digit_b.size()); // a と b の大きい方
vector<int> digit_ans(N); // 長さ N の配列 digit_ans を作る
for(int i = 0; i < N; ++i) {
digit_ans[i] = (i < digit_a.size() ? digit_a[i] : 0) - (i < digit_b.size() ? digit_b[i] : 0);
// digit_ans[i] を digit_a[i] - digit_b[i] にする (範囲外の場合は 0)
}
return carry_and_fix(digit_ans); // 2-4 節「繰り上がり計算」の関数です
}
繰り下がりも最大 $N$ 回しかなさそうです。だから、引き算の計算時間は $O(N)$ です!
実はこのプログラム、コメントアウトや関数の名前を除いて、大きな数の足し算の実装例とたった 1 文字しか違いません。さあ、どこでしょう?
# 2-4. 繰り上がり計算
足し算の繰り上がりと、引き算の繰り下がりを、1 つの関数でまとめて対処できると、実装がしやすいです。
繰り上がり・繰り下がりは、次のようなものと考えられます。
- 繰り上がり:ある桁を $10$ 引いて、その次の桁を $1$ 足す
- 繰り下がり:ある桁を $10$ 足して、その次の桁を $1$ 引く
筆算を思い出しましょう、一番下の位から繰り上がり/繰り下がりの計算をします。この桁が 0~9 になるまで、繰り上がり/繰り下がりを、くりかえすんですよね。
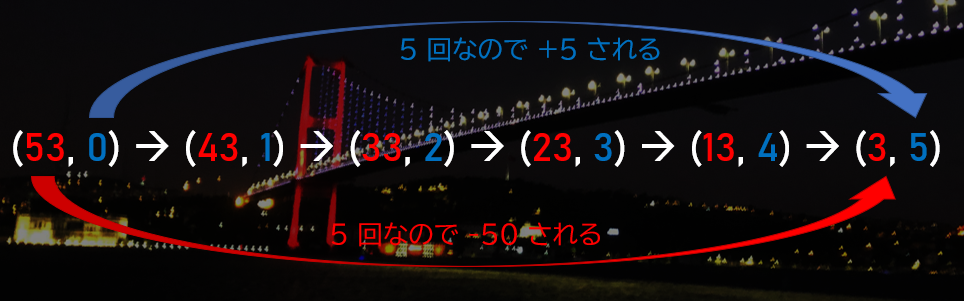
ちなみに、2 つの数の足し算・引き算ではありえない状態ですが、ある桁の数字が $20$ 以下の場合や $-10$ 以下になる場合にもうまくいきます。例を見てみましょう。
例:配列 (9, 23, -7, 15, 9) の繰り上がり/繰り下がり
例えば、配列 $(9, 23, -7, 15, 9)$ を繰り上がり/繰り下がりすると、どうなるでしょうか?
- まず 1 の位は、0 以上 9 以下なので OK
- 次に 10 の位の繰り上がりをする。(9, 23, -7, 15, 9) → (9, 13, -6, 15, 9) → (9, 3, -5, 15, 9)
- 次に 100 の位の繰り下がりをする。(9, 3, -5, 15, 9) → (9, 3, 5, 14, 9)
- 次に 1000 の位の繰り上がりをする。(9, 3, 5, 14, 9) → (9, 3, 5, 4, 10)
あれ?10000 の位が 10 になりましたね。桁数が足りないということなので、増やしましょう。
- 最後に 10000 の位の繰り上がりをする。(9, 3, 5, 4, 10, 0) → (9, 3, 5, 4, 0, 1)
- これで「104539」の繰り上がり/繰り下がりが完了!
大きな数の場合への対処
しかし、配列に $1000000$ や $-5000000$ など大きい値が出てきたらどうしましょう。これは、1 度に 10 ずつ繰り上がりをしていけば、時間がかかってしまいますよね。
ここで「値が $0~9$ になるまでに何回繰り上がりするか」を考えてみましょう!例えば先ほどの例で、「23」は 2 回の繰り上がりをしていました。
- 配列の値が $0$ 以上 $9$ 以下なら、繰り上がり/繰り下がりは必要ない
- $10$ 以上の整数 $X$ には、繰り上がりが「$X \div 10$ の商」回かかる
- $0$ 未満の整数 $-X$ には、繰り下がりが「$(X - 1) \div 10$ の商 + 1」回かかる
繰り上がりが $K$ 回ある場合、この桁を $10K$ 引いて、次の桁を $K$ 足せばよいです。
逆に、繰り下がりが $K$ 回ある場合は、この桁を $10K$ 足して、次の桁を $K$ 引けばよいです。
先ほど書いた通り、繰り上がり処理の前の配列の値が $1000000$ とか大きくなる場合でも、1 回の割り算で繰り上がり/繰り下がりの回数で求められます。
したがって、全部の桁を $0~9$ にする「整理」は、計算時間 $O(N)$ でできます!
繰り上がり処理の実装の例
C++ で実装すると、次のようになります。ここは少し複雑ですが、その分、足し算・引き算、さらには掛け算までが簡単に実装できるようになります!
C++ 以外のプログラミング言語を使っている読者さんも、さっきまでの説明が分かっていれば、この実装プログラムを見ながらでも、きっと自力で実装できると思います!
vector<int> carry_and_fix(vector<int> digit) {
int N = digit.size();
for(int i = 0; i < N - 1; ++i) {
// 繰り上がり処理 (K は繰り上がりの回数)
if(digit[i] >= 10) {
int K = digit[i] / 10;
digit[i] -= K * 10;
digit[i + 1] += K;
}
// 繰り下がり処理 (K は繰り下がりの回数)
if(digit[i] < 0) {
int K = (-digit[i] - 1) / 10 + 1;
digit[i] += K * 10;
digit[i + 1] -= K;
}
}
// 一番上の桁が 10 以上なら、桁数を増やすことを繰り返す
while(digit.back() >= 10) {
int K = digit.back() / 10;
digit.back() -= K * 10;
digit.push_back(K);
}
// 1 桁の「0」以外なら、一番上の桁の 0 (リーディング・ゼロ) を消す
while(digit.size() >= 2 && digit.back() == 0) {
digit.pop_back();
}
return digit;
}
第 2 章の前半のまとめ
ここまで長くなってしまいました。2-1 節から 2-4 節の内容をまとめると、以下の通りです!
- 大きな数を扱うときは、配列などを使って 1 桁ごとに値を管理しなければなりません
- $N$ 桁の足し算と引き算は、ともに計算時間 $O(N)$ でできます!
- $N$ 桁の数の「繰り上がり処理」も、計算時間 $O(N)$ でできます!
ここで練習問題です。$2^{1000}$ の値をプログラムを使って計算しましょう!
実は、ここまでの知識だけでこの問題は解けます。
2-5. 大きな数の掛け算
2-4. 節までで、$N$ 桁の足し算と引き算は $O(N)$ でできることが分かりました。
掛け算はどうでしょうか? 1-3 節「計算回数をかぞえてみよう」で述べたように、筆算をやるときは $N^2$ 回オーダーの計算が必要ですから、計算時間は $O(N^{2})$ になりそうですね。
もちろん筆算を実装することもできます。でも、もっと簡単な方法があります。2-4 節の「繰り上がり処理」の方法を使うことによって、こんな感じで計算することもできます!
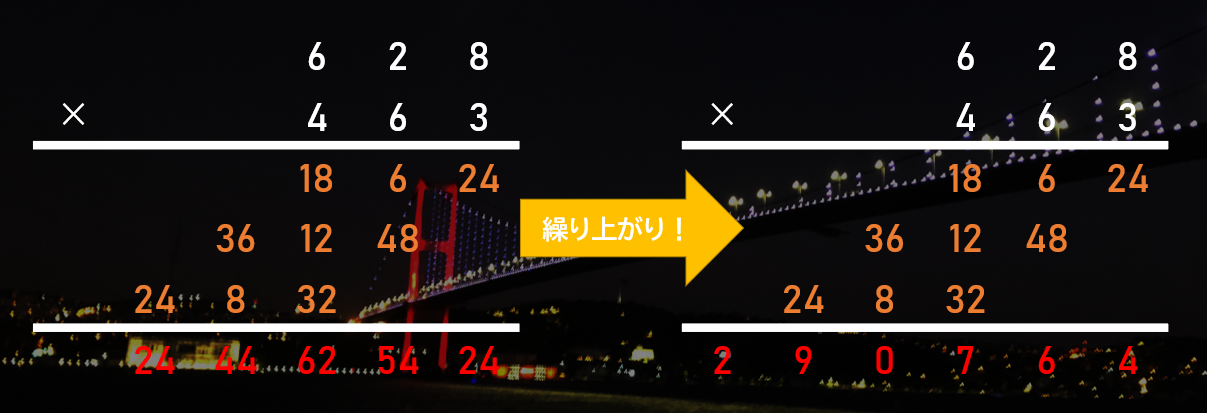
原理は同じです。ただ、筆算の繰り上がりをそのままの桁のところに書いただけです。
上の図の例でいう $(24, 54, 62, 44, 24)$ のような赤い部分の配列を「繰り上がり処理」すると $(4, 6, 7, 0, 9, 2)$ となり、正しい答え「290764」が求められます!
2-5-2. どうしてこれが正しいの?
そう思った人も多いかと思います。小学校でやった掛け算の筆算よりアルゴリズムが簡単なのに、なぜ?おそらく、そう思った人の多くが、掛け算の筆算がなぜ正しく動くのかの理由を考えたことがあまりないと思うので、ここで説明してしまいます。
例えば、$628 \times 463$ は、下図で表される長方形の面積 [$cm^{2}$] で表されます。下図の中には、上の筆算の図のオレンジで書かれた数が、たくさん見つかると思います。
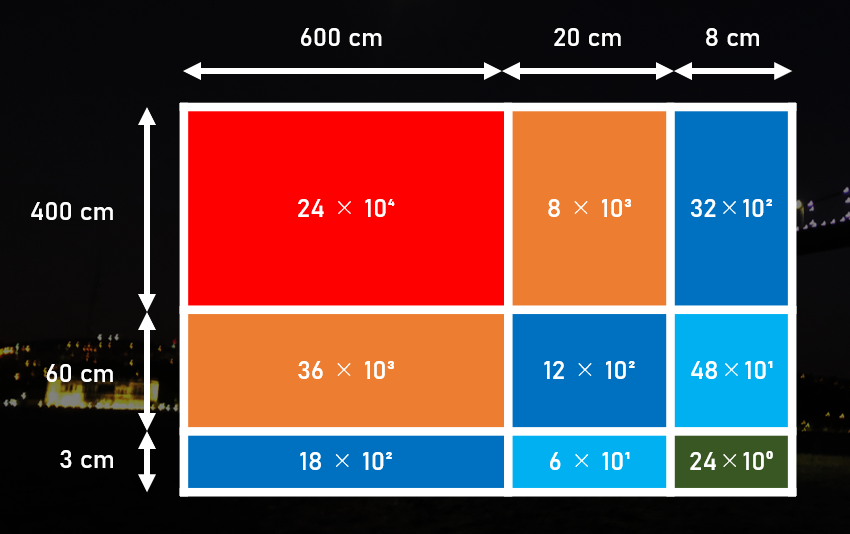
色は (1 つ目の数の位) $\times$ (2 つ目の数の位) によって決まっています。2-4 節のような「繰り上がり処理」を行う前の時点で、
| 1 の位 | 10 の位 | 100 の位 | 1000 の位 | 10000 の位 |
|:------:|:------:|:------:|:------:|:------:|:------:|
| 緑色 | 水色 | 青色 | 橙色 | 赤色 |
で表されています。それぞれの色の面積を、上の図を見て計算してみましょう。
- 緑色:$3 \times 8 = 24 cm^{2}$
- 水色:$(3 \times 2 + 6 \times 8) \times 10 = 540 cm^{2}$
- 青色:$(3 \times 6 + 6 \times 2 + 4 \times 8) \times 100 = 6200 cm^{2}$
- 橙色:$(6 \times 6 + 4 \times 2) \times 1000 = 44000 cm^{2}$
- 赤色:$4 \times 6 \times 10000 = 240000 cm^{2}$
これで、(1 の位, 10 の位, 100 の位, 1000 の位, 10000 の位) = $(24, 54, 62, 44, 24)$ としてもいいことが分かりましたね。これに「繰り上がり処理」をすれば $(4, 6, 7, 0, 9, 2)$ になって答え「290764」が求められる、という仕組みです!
2-5-3. 大きな数の掛け算を実装しよう!
筆算ベースのこのアルゴリズムを使ったとき、$N_{1}$ 桁の数と $N_{2}$ 桁の数の掛け算は、計算時間 $O(N_{1} \times N_{2})$ で求められそうです。さっきの長方形の図だと、これが $N_{1} \times N_{2}$ 分割されるので、計算回数もこのくらいになりそうですね?
特に、$N$ 桁 × $N$ 桁の掛け算の場合、計算時間は $O(N^{2})$ になります。
実装するとこんな感じです。「繰り上がり処理」を使えば、意外と単純です!1
vector<int> multiplication(vector<int> digit_a, vector<int> digit_b) {
int NA = digit_a.size(); // A の桁数
int NB = digit_b.size(); // B の桁数
vector<int> res(NA + NB - 1);
for(int i = 0; i < NA; ++i) {
for(int j = 0; j < NB; ++j) {
res[i+j] += digit_a[i] * digit_b[j];
// 答えの i+j の位に digit_a[i] * digit_b[j] を足す
}
}
return carry_and_fix(res);
}
2-5-4. 畳み込みについて (おまけ)
大きな数の計算とは直接関係ない話ですが、大きな数の掛け算と似ているので、畳み込み2 について説明しましょうか。次の問題を考えてみましょう。
配列 $A = (A_0, A_1, \dots, A_{N-1})$ と $B = (B_0, B_1, \dots, B_{M-1})$ が入力される。
- $0, 1, 2, \dots, N-1$ が書かれた赤いカードはそれぞれ $A_0, A_1, \dots, A_{N-1}$ 枚ある。
- $0, 1, 2, \dots, M-1$ が書かれた青いカードがそれぞれ $B_0, B_1, \dots, B_{M-1}$ 枚ある。
赤いカードを 1 枚、青いカードを 1 枚選ぶ。このとき、2 枚のカードに書かれた数を足すと $0, 1, 2, \dots, N+M-2$ のいずれかになるが、それぞれの場合について、選び方が何通りあるか計算してください。
例えば、$N = 3, M = 3$ のパターンで、$A = (8, 2, 6)$ と $B = (3, 6, 4)$ が入力された場合、2 枚のカードに書かれた数の合計が $0, 1, 2, 3, 4$ となる選び方はそれぞれ $(24, 54, 62, 44, 24)$ 通りです。
これが「畳み込み」です!例えば、2 つの配列 $(8, 2, 6)$ と $(3, 6, 4)$ を畳み込みすると、$(24, 54, 62, 44, 24)$ になる、ということです。なんか既視感ありませんか…?
そう!先ほどの例で、$628 \times 463$ の掛け算が出てきましたが、これが「繰り上がり処理」をする前の、計算結果を表す配列になっていますね~。つまり、
畳み込みができれば、あとは繰り上がり処理をするだけで掛け算の計算結果が求められる
ということです!
大きな数の掛け算と畳み込みとの関係性はつかめたでしょうか?普通に実装すると、長さ $N$ の配列と長さ $M$ の配列は、計算時間 $O(N \times M)$ で畳み込みできます。実はもっと高速な方法もあります。これは第 3 章を読んでいけば、きっと分かると思います…!
多項式の掛け算との関連性
例えば、$P(x) = 8 + 2x + 6x^2, Q(x) = 4 + 6x + 3x^2$ として、$P(x) \times Q(x)$ を計算します。
これは $24 + 54x + 62x^2 + 44x^3 + 24x^4$ です。畳み込みの結果と同じになるのは、$P(x) \times Q(x)$ の式を展開してみると、理由が分かってくると思います。
つまり、畳み込みをするのは、多項式を掛け算することと同じということなんです!
2-6. 大きな数の割り算
足し算・引き算・掛け算が終われば、次は割り算も実装したいですよね?
小学校だと、割り算は四則演算の中で一番最後に習う内容です。人によっては、割り算の筆算に苦しんだ思い出があるかもしれません。4 つの四則演算の筆算の中で、最も複雑なアルゴリズムです。
試しに、$1111111 ÷ 4649$ の商を、筆算で計算してみましょう!

こんな感じです!具体的には、こんな感じで動いています。少し複雑なプログラムを実装する際には、ひとつの具体例について「どんな感じでプログラムを動かしたいか」考えると良いです。
- 桁数:$464900 \leq 1111111 < 4649000$ なので、答えは 3 桁になることが分かる
- 100 の位:$4649×2 \leq 11111 < 4649×3$ なので、答えの 100 の位は「2」で、$11111 - 4649×2 = 1813$ が降りる
- 10 の位:$4649×3 \leq 18131 < 4649×4$ なので、答えの 10 の位は「3」で、$18131 - 4649×3 = 4184$ が降りる
- 1 の位:$4649×9 \leq 41841 < 4649×10$ なので、答えの 1 の位は「9」で、$41841 - 4649×9 = 0$ が降りる
- あまり:降りてきたのが $0$ なので、$1111111 ÷ 4649$ のあまりは「0」
こんな感じで割り算ができますね。偶然なことにも、1111111 は 4649 で割り切れます。
2-6-2. 割り算の計算時間はどのくらい?
まず、筆算で 1 段下げる (商の 1 つの桁を求める) のにどんな計算をしているか考えましょう。
例えば、先ほどの例の 10 の位の場合、$18131$ と比べて $4649$ $\times$ (いくつ) が初めて大きくなるかを、こんな感じで調べる必要があります。
- $18131$ より $4649 \times 1 = 4649$ の方が大きいか? → NO
- $18131$ より $4649 \times 2 = 9298$ の方が大きいか? → NO
- $18131$ より $4649 \times 3 = 13947$ の方が大きいか? → NO
- $18131$ より $4649 \times 4 = 18596$ の方が大きいか? → YES
- これで、商の 10 の位が「3」と分かった!
各ステップでは、次の 2 つのことをやっています。(これを [操作A] とします)
- $M$ 桁 × $1$ 桁の掛け算 ー これには計算時間 $O(M)$ がかかる
- $M$ 桁くらいの $2$ つの数の比較 ー これにも計算時間 $O(M)$ かかる
つまり、各ステップの計算時間は $O(M)$ です。これを「×1 はどうかな?」「×2 だとどうかな?」…「×9 でどうかな?」までやるので、この 9 倍です。だから、筆算で 1 段下げる (商の 1 つの桁を求める) のに計算時間 $O(M)$ かかります。
計算時間 $O(M)$ とはいえ、定数倍はざっと見積もって $2 \times 9 = 18$ かかっています。つまり、見た目よりも動作が遅いと思った方がよいでしょう。
$N$ 桁 ÷ $M$ 桁の割り算の商の桁数は、大体 $N-M$ 桁くらいになります。よって、[操作A] が大体 $N-M$ 回だから、計算時間は $O(M × (N-M))$、と見積もることができます。
つまり、「N 桁 ÷ 1 桁の割り算」「N 桁 ÷ N-1 桁の割り算」などは、計算時間 $O(N)$ なので速いですが、$N$ 桁 ÷ $(N/2)$ 桁の割り算などは、計算時間 $O(N^2)$ なので遅いです。計算時間の定数倍が大きいことを考えると、例えば ($20000$ 桁) ÷ ($10000$ 桁) の割り算にも数十秒かかりそうです。
しかし、もっと高速なアルゴリズムもあります!これは第 3 章のお楽しみに。
2-6-3. まずは大小比較の実装から
割り算をするためには、大小比較をする必要があります。桁数が違う数の大小比較は簡単です。同じ場合も、2 つの数の桁が違う一番大きい位 (一番左のところ) の大小で決まります。
例えば、123456789 と 123498765 は、後者の方が大きいです。なぜなら桁数も「1234」も同じで、初めて値が違う 10000 の位が前者が小さい「5」に対して後者が大きい「9」となっているからです。
2 つの数 $A, B$ が、それぞれ配列 $(a_0, a_1, \dots, a_{N_A - 1})$ と $(b_0, b_1, \dots, b_{N_B - 1})$ で表されているとき:
- $N_A > N_B$ ならば、$A$ の方が桁数が多いので、$A$ が大きい!
- $N_A < N_B$ ならば、$B$ の方が桁数が多いので、$B$ が大きい!
- もし $N_A = N_B$ の場合、この桁数を $N$ とすると…?
- $10^{N-1}$ の位:もし $a_{N-1}$ と $b_{N-1}$ が違えば、これが大きい方が大きい。$a_{N-1} = b_{N-1}$ ならば、この時点では分からない
- $10^{N-2}$ の位:もし $a_{N-2}$ と $b_{N-2}$ が違えば、これが大きい方が大きい。$a_{N-2} = b_{N-2}$ ならば、この時点では分からない
- ... (中略) ...
- $10$ の位:もし $a_1$ と $b_1$ が違えば、これが大きい方が大きい。$a_1 = b_1$ ならば、この時点では分からない
- $1$ の位:もし $a_0$ と $b_0$ が違えば、これが大きい方が大きい。$a_0 = b_0$ ならば、2 つの数は同じ
意外と単純ですね!?例えば、C++ で実装するとこんな感じになります。
下の compare_bigint 関数は、2 つが等しいなら「0」、左が大きいなら「+1」、右が大きいなら「-1」を返す関数となっています。
int compare_bigint(vector<int> digit_a, vector<int> digit_b) {
int NA = digit_a.size(); // A の桁数
int NB = digit_b.size(); // B の桁数
if(NA > NB) return +1; // 左が大きい
if(NA < NB) return -1; // 右が大きい
for(int i = NA - 1; i >= 0; --i) {
if(digit_a[i] > digit_b[i]) return +1; // 左が大きい
if(digit_a[i] < digit_b[i]) return -1; // 右が大きい
}
return 0;
}
2-6-4. いざ割り算を実装してみよう!
さて、大小比較ができたところで、割り算を実装してみましょう!
少し複雑なので、特に C++ を使っていない人などで、下のプログラムが何をやっているか分からない人は、自分の思うように「大きな数の割り算」のプログラムを実装してみるのもよいかと思います。
vector<int> division(vector<int> digit_a, vector<int> digit_b) {
int NA = digit_a.size(), NB = digit_b.size();
if(NA < NB) return { 0 };
// ----- ステップ 1. A ÷ B の桁数を求める ----- //
int D = NA - NB;
// digit_a_partial : A の上 NB 桁を取り出したもの
vector<int> digit_a_partial(digit_a.begin() + (NA - NB), digit_a.end());
if(compare_bigint(digit_a_partial, digit_b) >= 0) {
// (A の上 NB 桁) が B 以上だったら...?
D = NA - NB + 1;
}
// ----- ステップ 2. A ÷ B を筆算で求める ----- //
if(D == 0) return { 0 };
vector<int> remain(digit_a.begin() + (D - 1), digit_a.end());
vector<int> digit_ans(D);
for(int i = D - 1; i >= 0; --i) {
digit_ans[i] = 9;
for(int j = 1; j <= 9; ++j) {
vector<int> x = multiplication(digit_b, { j });
if(compare_bigint(x, remain) == 1) {
digit_ans[i] = j - 1;
break;
}
}
vector<int> x_result = multiplication(digit_b, { digit_ans[i] });
remain = subtraction(remain, x_result);
if(i >= 1) {
// 新しく 10^(i-1) の位が降りてくる
remain.insert(remain.begin(), digit_a[i - 1]);
}
}
return digit_ans;
}
この実装例では、割り算のあまりは、最終的な remain の値になっていると思います。
筆算では、割り算の商とあまりを同時に求めているので、よさそうですね?
2-7. ここまでのまとめ
お疲れ様でした、これで大きな整数の計算が一通り実装できました!
第 2 章で書いたのは、正の整数の入力・出力・大小比較・足し算・引き算・掛け算・割り算です!
例えば、上に書いた大きな数の計算のプログラムを全部載せた上で3、次のようにプログラムを書いてみます。
int main() {
string S, T;
cin >> S >> T;
vector<int> NS = string_to_bigint(S);
vector<int> NT = string_to_bigint(T);
vector<int> ans = division(NS, NT);
cout << bigint_to_string(ans) << endl;
return 0;
}
例えば、123456789 54321 と入力します。すると、正しく「2272」が表示されていると思います。
ライブラリさえ最初に作ってしまえば、大きな数は int 型と実質同じような感じで扱えます!
C++ などのプログラミング言語を使っている場合、大きな数のクラスを作って、演算子のオーバーロードを実装すると、さらに使い勝手がよいかもしれません。
この基本的な四則演算さえできれば、高速ではないにしろ、4 章に載っているような応用的なこともできます。世の中の色々な計算は、足し算・引き算・掛け算・割り算がもとになっていますからね。
2-7-2. 計算時間について
筆算ベースのアルゴリズムでの、足し算・引き算・掛け算・割り算にかかる計算時間をまとめます。
| 計算の種類 | N 桁と N 桁 | N1 桁と N2 桁 (N1 > N2) |
|---|---|---|
| 足し算 | 計算時間 $O(N)$ | 計算時間 $O(N_1)$ |
| 引き算 | 計算時間 $O(N)$ | 計算時間 $O(N_1)$ |
| 掛け算 | 計算時間 $O(N^2)$ | 計算時間 $O(N_1 \times N_2)$ |
| 割り算 | 計算時間 $O(N^2)$* | 計算時間 $O(N_2 \times (N_1 - N_2))$ |
| (注*:割り算については、$N$ 桁 ÷ $(N/2)$ 桁の計算について書いています) |
筆算ベースのアルゴリズムだと、速さ順には (足し算) = (引き算) < (掛け算) < (割り算) と思っておくとよいと思います。実際に、割り算は掛け算よりも 10 倍程度遅いです。
しかし、これは小学校で習うような筆算でやった場合です。現代では、もっと高速に計算する方法が見つかっています!すべての始まりは 1960 年でした… 次の 3 章は、「60 年前」という数学の歴史ではつい最近の出発点からの高速なアルゴリズムを解説していきます。
それでは準備はいいですか?
3. 多倍長整数演算 ~理論編~
第 2 章で説明した「筆算」ベースのアルゴリズムでは、$N$ 桁の足し算と引き算の計算時間は $O(N)$ でした。これはこれ以上高速化のしようがないことは、分かると思います。
しかし、掛け算と割り算の計算時間は $O(N^2)$ です。$N$ 桁オーダーを読み取って、$N$ 桁オーダーの値を計算する。これに $O(N^2)$ かかっているのです。まだ改善できそうではありませんか!
みなさんは小学生の時、例えば 4 桁 × 4 桁の掛け算の計算に時間がかかり、「もっと速く掛け算する方法はないのか?」と考えたことがあるかもしれません。実は、4 桁 × 4 桁などの (コンピューターにとっては) 小さいサイズの掛け算では、計算回数の面では筆算がほぼ最適です。
しかし、1000 桁 × 1000 桁となると、事情が変わってきます。計算回数 100 万回もかかるでしょうか?実はもっと速いアルゴリズムがあります。でもこの問題は、多くの人が疑問を持っておきながら、解決されたのは意外と最近のことなのです。
3-1. 1960 年 ~すべての始まり~
1960 年の秋、ソビエト連邦、モスクワ大学。
当時 57 才の有名な数学者 アンドリー・コルモゴロフ さん4が、計算理論のセミナーを開いていました。
この時に彼は言いました。「$N$ 桁 × $N$ 桁の掛け算は、計算時間 $O(N^2)$ より速いアルゴリズムがないことが予想されているよ。」
このセミナーを受けていた 23 才の アナトリー・カラツバ さんは、これから 1 週間も経たずに、$O(N^2)$ より高速な掛け算のアルゴリズムを思いついてしまったのです!これが 3-2 節で解説する「カラツバ法」です。
この瞬間を原点にして、掛け算や割り算のアルゴリズムが次々と高速化され、その後に $\sqrt{2} = 1.4142...$ や円周率 $\pi = 3.1415...$ の値の計算が、一気に精度よく進むようになったほか、RSA 暗号などにも使われる素数判定も高速になったりとか、次の数十年で色々進歩しました!
3-2. 画期的な掛け算の方法、カラツバ法!
まずは、この原点になった 1962 年に発表された「カラツバ法」を解説します。
1960 年の発明だから、難しいのではないか?と思うかもしれませんが、意外とシンプルです!
中学生でも理解できる人は多いかと思います。
3-2-1. N 桁の掛け算を小さな問題に分割
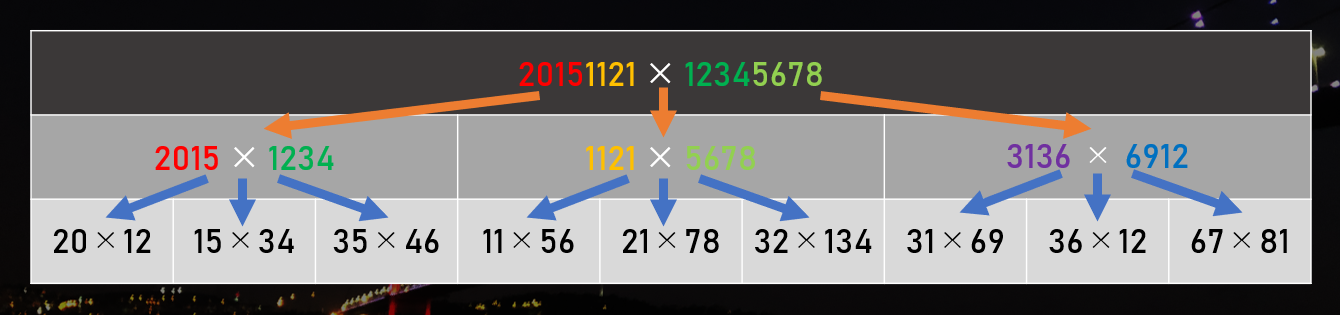
例として、8 桁 × 8 桁の掛け算「$20151121 \times 12345678$」を計算してみます。
その際に、上 4 桁と下 4 桁で分けてみましょう。こんな感じで計算できます。

なんで 20151121 × 12345678 = 2015×1234×10⁸ + ... + 1121×5678 になるのでしょうか?これは、2-5. 節の掛け算のところで出てきた図のように、長方形を縦で 2 分割、横で 2 分割すると、分かりやすいです。(数学的にいえば、「式の展開」の話とつながってきます。これは中学 3 年の数学で習う内容ですので、高校生以上の読者や、式の展開を知っている人は、展開のイメージで考えてもよいでしょう。)
結果的に、8 桁 × 8 桁の掛け算「$20151121 \times 12345678$」は、**4 桁 × 4 桁の掛け算 4 つの答えを求める問題に「落とし込む」ことができました。**これが終われば、あとは足し算 (これは桁数に比例する計算時間でできるので速いです!) をするだけです!
桁数が $N$ の場合 (一般の場合) を考えると、$N$ 桁 × $N$ 桁の掛け算は、おおよそ $(N/2)$ 桁 × $(N/2)$ 桁の掛け算の問題 4 つに落とし込むことができます!
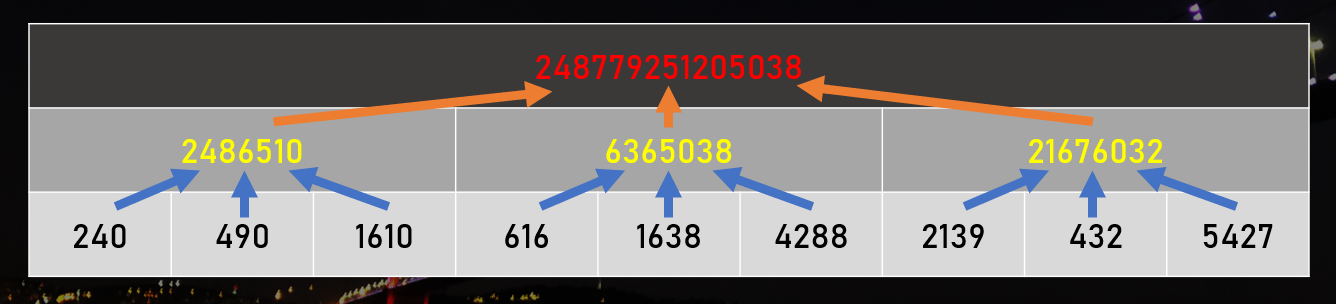
今、20151121 × 12345678 で、以下の 3 つを求める問題に落とし込むことができましたね。これについて、少し考えを深めてみましょう。
- 2015 × 1234 (これは 10⁸ 倍されて足される)
- 1121 × 1234 + 2015 × 5678 (これは 10⁴ 倍されて足される)
- 1121 × 5678 (これはそのまま足される)
これについて、少し考えを深めてみましょう。
- 1 つ目の式「2015 × 1234」は、1 回の掛け算でできてるので、これ以上改善できそうにない
- 3 つ目の式「1121 × 5678」も、1 回の掛け算でできてるので、これ以上改善できそうにない
この 2 つは、これ以上改善できそうにないですね。
残った 1 つの式は「1121 × 1234 + 2015 × 5678」です。これは 2 回の掛け算で求めています。これも改善できそうに… ないですよね…
いや、ちょっと待った!本当に改善できないですか???
3-2-2. (N/2) 桁 × (N/2) 桁の掛け算 3 つにする魔法
実は、さっき残った 1 つの式「1121 × 1234 + 2015 × 5678」は、"魔法" を使えばたった 1 回の掛け算で計算できるのです!
こんな魔法、本当にあるのでしょうか?と思うかもしれません。こんなことができるならば、$20151121 \times 12345678$ の計算が、たった 3 つの 4 桁 × 4 桁の掛け算に落とし込めてしまいます。
2 つ目の式について、よく考えてみると…?
- 1121 × 1234 + 2015 × 5678 = (2015 + 1121) × (1234 + 5678) - 2015 × 1234 - 1121 × 5678
あれ?よく見てください。なんと 2015 × 1234 と 1121 × 5678 は、「1 つ目の式」と「3 つ目の式」として、既に計算されているではありませんか!
つまり、(2015 + 1121) × (1234 + 5678)、すなわち 3136 × 6912 の計算結果さえ分かれば、あとは引き算をするだけで「2 つ目の式」の計算結果が求まるんです!

これは、この魔法のようなアルゴリズムを使えば、「$N$ 桁 × $N$ 桁の掛け算の計算量」は「$(N/2)$ 桁 × $(N/2)$ 桁の掛け算 3 つの計算量」と同じにできる5ことを意味しています。
そんなことある?私だって初めてカラツバ法を知った時はそう思いました。
だって、「$20151121$ だから $2015+1121=3136$」と、「$12345678$ だから $1234+5678=6912$」みたいな、見るからにテキトーな感じのことを掛け算して、実際にめっちゃ上手くいってるんですよね。マジで魔法ですね。
しかし、読んでいるあなたは、そう思うかもしれません。
- $(N/2)$ 桁 $\times$ $(N/2)$ 桁の掛け算の計算時間が $(N/2)^{2}$ = $N^{2} \times 0.25$ 回で、これが 3 回で $N^2 \times 0.75$ 回。
- だから、3/4 倍の高速化にしかなっていないのでは?
そんなことはありません!あと一工夫で、計算量を $O(N^{2})$ から減らせます。
もう一歩手前まで来ています!
3-2-3. N÷2 桁の掛け算 3 つにもさらに魔法が使える!
実は、$N/2$ 桁の掛け算 3 つにも、さっきと同じ魔法を適用させてみましょう。
ほい、$N/4$ 桁の掛け算 9 つに落とし込むことができました!
そして、$N/4$ 桁の掛け算 9 個にも、さっきと同じ魔法を適用させてみましょう。
すると、$N/8$ 桁の掛け算 27 個に落とし込むことができました!
さらに、$N/8$ 桁の掛け算 27 個にも、さっきと同じ魔法を適用させてみましょう。
すると、$N/16$ 桁の掛け算 81 個に落とし込むことができました!
この「落とし込み」を繰り返すと、例えば 1024 桁 × 1024 桁の掛け算は、どうなるでしょうか?
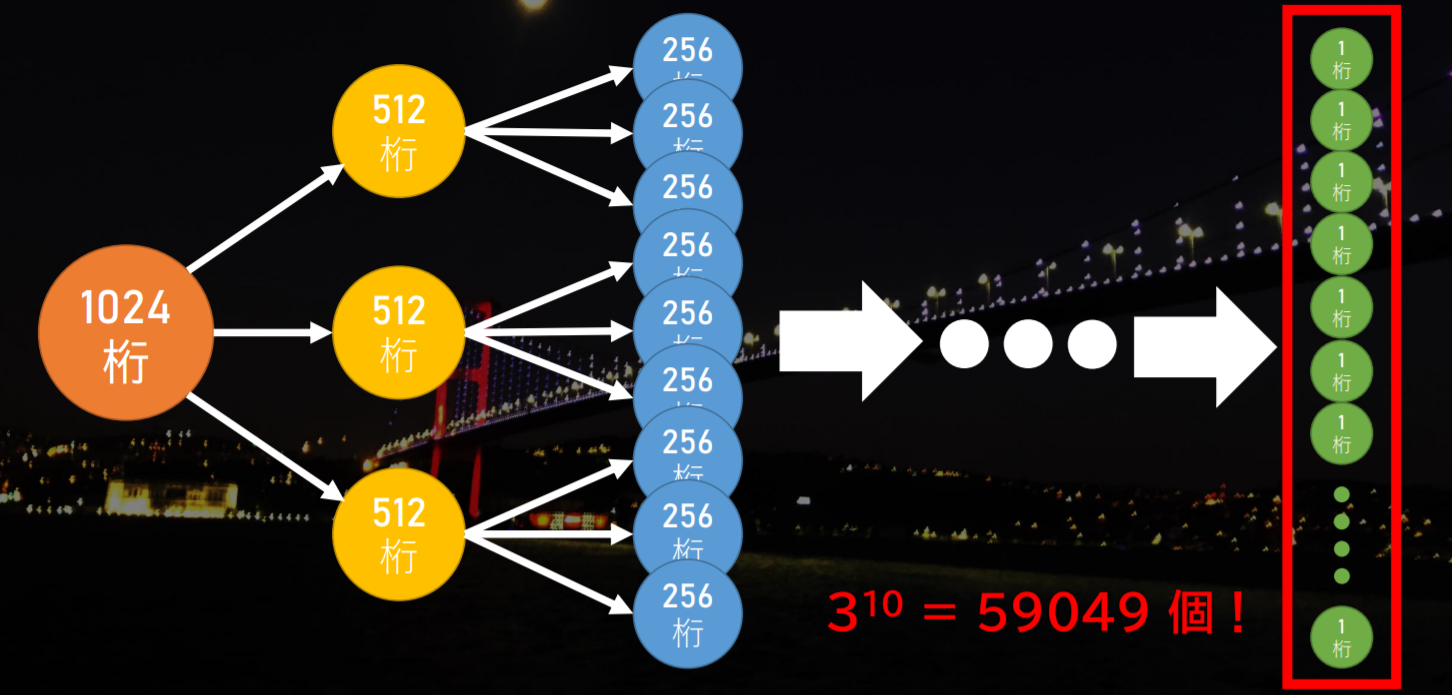
そう!1 桁 × 1 桁の掛け算6を、$3^{10} = 59049$ 個に落とし込むことができました。これさえできれば、あとは時間のかからない足し算と引き算だけで、2048 桁にわたる掛け算の結果が求まるんです。イメージとしては、九九の計算問題を 59049 回解いて、あとは適切に足し算と引き算をしてやれば、1024 桁 × 1024 桁の掛け算の計算結果が求まる、と思ってよいでしょう。
3-2-4. カラツバ法の計算量
例えば、1024 桁 × 1024 桁の掛け算について考えてみましょう。計算内容は「みなし」です。例えば最下段では 1 桁の掛け算ということになっていますが、3 桁までならありえます。しかし、1 桁の掛け算とみなしても計算時間のオーダーは変わりません。
| 段 | 計算内容 (みなし) | 計算回数 (みなし) |
|---|---|---|
| 最下段 | 1 桁の掛け算が $3^{10}$ 回 | $3^{10}$ 回 |
| 2 段目 | 2 桁の足し算・引き算がそれぞれ $3^{9} \times 2$ 回 | $3^{9} \times 4$ 回 |
| 3 段目 | 4 桁の足し算・引き算がそれぞれ $3^{8} \times 2$ 回 | $3^{8} \times 4$ 回 |
| : | : | : |
| 10 段目 | 512 桁の足し算・引き算がそれぞれ $3^{1} \times 2$ 回 | $3^{1} \times 4$ 回 |
| 11 段目 | 1024 桁の足し算・引き算がそれぞれ $3^{0} \times 2$ 回 | $3^{0} \times 4$ 回 |
これを合計して、全体の計算回数を見積もってみましょう。ほとんど $3^{10} \times 3$ と同じになっています。だから、計算回数は $3^{10}$ $\times$ (定数倍) と考えられそうですね。
$N = 2^{n}$ の場合だと、これが「ほぼ $3^{n} \times 3$ 回」になるので、計算時間は $O(3^n)$ です。
これは、$N$ 桁 × $N$ 桁の掛け算が、カラツバ法を使うと計算時間 $O(N^{1.59})$ でできることを意味しています!
なぜ O(N1.59) なのか
高校 2 年生の数学で習う「対数関数」を使うと、$O(N^{1.59})$ である理由が分かります。
対数関数 $\log_a b$ は、$a^x = b$ となる $x$ のことです。具体的には、$\log_2 3$ は、$2^x = 3$ となる $x$ のことで、これは $x = 1.584962...$ です。
- $N = 2^n$ なので、$n = \log_2(N)$ と考えることができる
- カラツバ法を使った計算時間は $O(3^n) = O(3^{log_2 N})$
- ここで、$3^{\log_2(N)} = (2^{(\log_2 3)})^{\log_2 N} = (2^{(\log_2 N)})^{\log_2 3} = N^{\log_2 3}$ と計算できる
- だから、計算量は $O(N^{\log_2 3}) = O(N^{1.5849\dots}) ≒ O(N^{1.59})$ になっていると分かる!
これを見るに、100 万桁の掛け算でも、現代のパソコンでは数十秒程度で計算することができそうですね。大きな数の掛け算になればなるほど、筆算ベースでのアルゴリズムよりも速さが顕著になります。
3-2-5. カラツバ法の実装
カラツバ法の実装として、「再帰関数」を使う方法がよく使われています。
しかし、再帰関数は難しいんです。正直に言うと、私が中 1 の時に情報オリンピックの本選に行けて、この時は最短経路問題を解く「ダイクストラ法」も書けましたが、この時点でまだ再帰関数は書けませんでした。
だから今回は、再帰関数を使わずにカラツバ法を実装する方針を書きます!
ステップ 1
まずは、下図のような構造 (これを「カラツバ・ツリー」ということにする) を書きます。カラツバ・ツリーの段数 $D+1$ は、$2^{D}$ が桁数 $N$ 以上になるように設定します。例えば
- 1024 桁だと $D=10$、
- 10 万桁だと $D=17$
みたいな感じです。(下図では、図のレイアウト上、仕方なく $D=2$ にしています)
これは、一番上を番号 0、真ん中の段のマスの番号を左から順に 1, 2, 3、下の段のマスの番号を左から順に 4, 5, 6, 7, ..., 12、と振ると、実装しやすいと思います。そうすると、一つの配列を使って、番号 0 のマスから順に「このマスに?×?が入る」を計算することができます。7
ステップ 2
次に、カラツバ・ツリーの番号の大きいマスから順に、このマスに入る掛け算の結果を計算します。まずは一番下の段の計算を普通に終わらせます。それ以外の段は、下の 3 マスの計算結果が求まっている状態だと、足し算だけで計算することができます。7
カラツバ法は普通の掛け算に比べて計算時間の "定数倍" が大きいので、数十桁程度の掛け算ではカラツバ法よりも $O(N^2)$ のアルゴリズムの方が速いといわれています。だから、段数を $D-5$ にするなどあえて減らし、カラツバ・ツリーの一番下の段の掛け算の結果を筆算ベースの掛け算で求める、というのも一つの手です。
再帰関数を使う場合は「100 桁以内になったら再帰を打ち切って計算結果は筆算ベースの掛け算で求める」実装手段もあります。そうすると、計算時間のオーダーは変わりませんが、プログラムの実行が速くなります。
3-2-6. 畳み込みへの応用
カラツバ法は、元々は大きな数の掛け算として開発されたアルゴリズムですが、畳み込みにも応用することができます。アルゴリズムはほとんど同じなので、気になる人は自分で考えたり調べたりしましょう。
3-3. さらに速い!Toom-Cook 法
カラツバ法が発表された 1962 年から 1 年が経ちました。
1963 年、アンドレ・トゥームさんとスティーブン・クックさんによって、さらに速い掛け算のアルゴリズム「Toom-Cook 法」が開発されました!
3-3-1. N÷3 桁の掛け算 5 つに落とし込みたい!
カラツバ法は、$N$ 桁の掛け算を「$N/2$ 桁の掛け算 3 つ」に落とし込むことに成功し、$N$ 桁の掛け算の計算時間を $O(N^{1.59})$ にしました。
ここでおそらく彼らはそう考えたのでしょう。
- カラツバ法は $N$ 桁の掛け算を「$N/2$ 桁の掛け算 3 つ」に落とし込んだ。
- 同じように、$N$ 桁の掛け算を「$N/3$ 桁の掛け算 5 つ」に落とし込めないか?
なんとこれは、今から説明するような方法で、できます!
例えば、123456789 × 741852963 を計算することにしましょう。カラツバ法の考え方を使えば、次の 5 つの値が求まれば、あとは足し算するだけで元の答えが分かりますね。
- 123 × 741 (これは 1012 倍されて足される)
- 123 × 852 + 456 × 741 (これは 10⁹ 倍されて足される)
- 123 × 963 + 456 × 852 + 789 × 741 (これは 10⁶ 倍されて足される)
- 456 × 963 + 789 × 852 (これは 10³ 倍されて足される)
- 789 × 963 (これはそのまま足される)
この 5 つの値を求めることを、5 回の 3 桁 × 3 桁の掛け算でできれば、勝ちです。
ここで数学の問題!
ここで問題です!
2 次関数 $ax^{2} + bx + c$ の $x = 1$ の時の値が $1$、$x = 2$ の時の値が $5$、$x = 3$ の時の値が $7$ です。このとき、$a, b, c$ の値を求め、この 2 次関数を "復元" してください。
この式に $x = 1, 2, 3$ を代入すると、次の 3 つが成り立つことが分かるでしょう。
- x = 1 のとき: 2 次関数の式は「$a + b + c = 1$」… ①
- x = 2 のとき: 2 次関数の式は「$4a + 2b + c = 5$」… ②
- x = 3 のとき: 2 次関数の式は「$9a + 3b + c = 7$」… ③
この ①, ②, ③ の式の 連立方程式 を解くと、答えが $(a, b, c) = (-1, 7, -5)$ と求まります。
したがって、元の 2 次関数は「$-x^{2} + 7x - 5$」です。
これと同じ考え方が使える!
先ほどの例で、次の多項式を考えてみましょう。
$$P(x) = 123x^2 + 456x + 789, Q(x) = 741x^2 + 852x + 963$$
ここで $R(x) = P(x) \times Q(x)$ を、下の図のように示してみました。
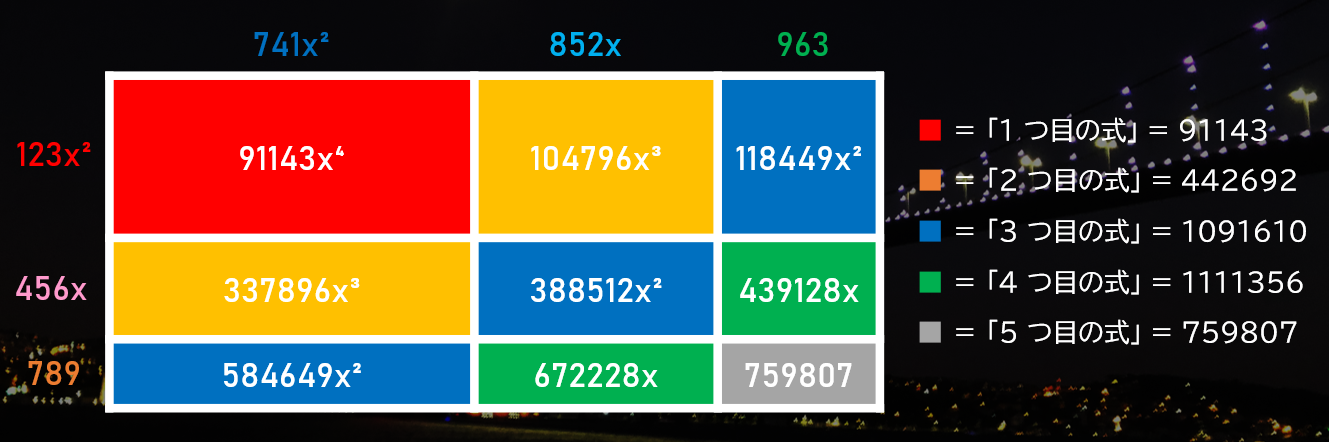
$x = 10^3$ のときに、長方形の面積が 123456789 × 741852963 になっていますね?
$R(x)$ の式は、$c_4 x^4 + c_3 x^3 + c_2 x^2 + c_1 x + c_0$ の形で表されます。この $c_4, c_3, c_2, c_1, c_0$ の値こそが、求める「1 つ目の式」~「5 つ目の式」なのです!
しかし、そのまま式の展開をしたら、上の図の 9 マスの面積をそれぞれ求めることになるので、$(N/3)$ 桁の掛け算を 9 回必要とします。これだと、計算時間 $O(N^2)$ から何の改善もしていません。
ここで、先ほどの問題の考え方が使えます! これは、$R(-2), R(-1), R(0), R(1), R(2)$ の値が分かれば、$c_4, c_3, c_2, c_1, c_0$ の値は連立方程式を使って復元できる、ということです!
- R(-2) = P(-2) × Q(-2) = (123×4 - 456×2 + 789) × (741×4 - 852×2 + 963) = 369 × 2223
- R(-1) = P(-1) × Q(-1) = (123 - 456 + 789) × (741 - 852 + 963) = 456 × 852
- R(0) = P(0) × Q(0) = 789 × 963
- R(1) = P(1) × Q(1) = (123 + 456 + 789) × (741 + 852 + 963) = 1368 × 2556
- R(2) = P(2) × Q(2) = (123×4 + 456×2 + 789) × (741×4 + 852×2 + 963) = 2193 × 5631
$N$ 桁 $\times$ $1$ 桁の掛け算は、筆算ベースのアルゴリズムで $O(N)$ で計算できるので、足し算と同じくらい "最高に速い" と思ってもよいです。これで、3~4 桁の掛け算 5 つに「落とし込め」ました。
この $R(-2), R(-1), R(0), R(1), R(2)$ が求まれば、連立方程式を使って $c_4, c_3, c_2, c_1, c_0$ の値を復元できますね?さて、解いてみましょう!
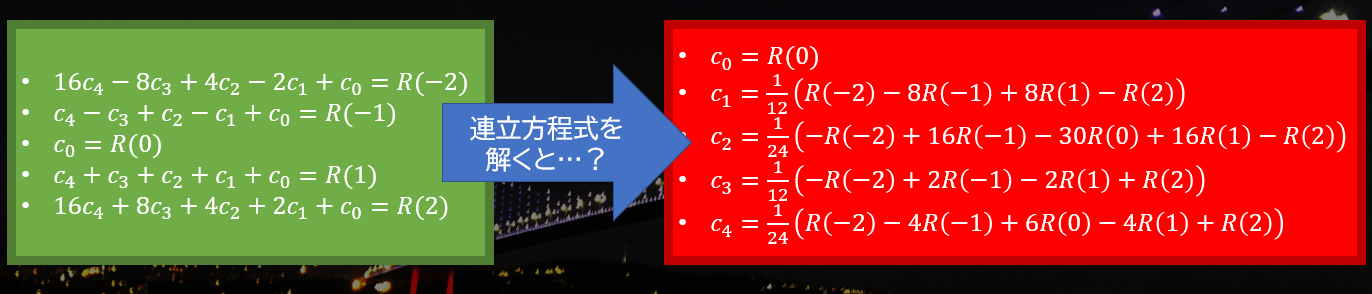
つまり、
- 足し算・引き算
- 16 や 30 などの小さな数で掛け算
- 12 や 24 の小さな数で割り算
だけをすることで「1 つ目の値」~「5 つ目の値」を全部復元できるということです。この計算時間は全部 O(N) です。
この方法を使うと、N 桁 × N 桁の掛け算は、5 つの (N/3) 桁 × (N/3) 桁の掛け算に落とし込め、エクストラに O(N) の計算時間しかかからないということです。
まさにカラツバ法で見たのと同じ構図です!
3-3-2. Toom-Cook-3 法の計算量は?
カラツバ法と同じ考え方で、$N = 3^n$ のときに計算時間が $O(5^n)$ になることが分かるでしょう。
よって、計算時間は $O(N^{\log_3 5}) = O(N^{1.464973...})$ になります。8
これが Toom-Cook-3 法9です!
3-3-3. Toom-Cook 法はどこまで…
第 3 章のここまでの内容を振り返ってみましょう。
- $N$ 桁の掛け算を「$N/2$ 桁の掛け算 3 つ」に落とし込むことで、$N$ 桁の掛け算を $O(N^{1.59})$ で計算できる!(カラツバ法)
- $N$ 桁の掛け算を「$N/3$ 桁の掛け算 5 つ」に落とし込むことで、$N$ 桁の掛け算を $O(N^{1.47})$ で計算できる!(Toom-Cook-3 法)
ここまで来れば、そう考える読者も多いと思います。
「$N/4$ 桁の掛け算 7 つに落とし込むことで、$N$ 桁の掛け算を $O(N^{1.41})$ で計算できないか?」
これは先ほどの Toom-Cook-3 法と同じアイデアで求められます!6 次多項式10は、7 個の x での値が求まれば復元できます。だから、$R(-3), R(-2), R(-1), R(0), R(1), R(2), R(3)$ を計算して、元の 6 次多項式 R(x) を連立方程式で復元してやればいいのです!
いわゆる「Toom-Cook-4 法」です。$N$ 桁の掛け算を、$N/4$ 桁の掛け算 7 つに落とし込むことができましたね!だから、計算時間 $O(N^{1.41})$ で掛け算できます。
みなさん、想像がつくと思いますが、この方法で Toom-Cook-5 法・Toom-Cook-6 法・Toom-Cook-7 法… も実現できてしまいます!
- 4 分割すると 6 次多項式を復元するので 7 個の掛け算、計算時間は $O(N^{1.404})$
- 5 分割すると 8 次多項式を復元するので 9 個の掛け算、計算時間は $O(N^{1.366})$
- 6 分割すると 10 次多項式を復元するので 11 個の掛け算、計算時間は $O(N^{1.339})$
- 7 分割すると 12 次多項式を復元するので 13 個の掛け算、計算時間は $O(N^{1.319})$
- $d$ 分割すると $2d-2$ 次多項式を復元するので $2d-1$ 個の掛け算、計算量は $O(N^{\log_d(2d+1)})$
$d$ の値を上げれば上げるほど計算量がどんどん小さくなので、どんどん速くなるのでは…?と思う読者さんもいると思いますが、世の中は厳しいので、そんな上手いこといきません。
Toom-Cook 法にも限界はある
多くに分割したら、連立方程式の解が大変なことになれば、計算が大変なことになってしまいます。
だから、全く速くならないどころか、むしろ遅くなってしまいます!例えば「Toom-Cook-100 法」が実用的かと言われると全く違い、計算時間の定数倍が超巨大になりますから、実用的な桁数では筆算ベースよりも遅くなるでしょう。
残念なことに Toom-Cook-5 以上は、実用的には速さで Toom-Cook-3 に負けてしまいます。
3-3-4. Toom-Cook-3 法の実装と改良
実装はカラツバ法に比べたら複雑ですが、連立方程式の解などはその通りに計算すればいいだけなので、やばいことにはならないと思います。
また、実用的には、$R(-2), R(-1), R(0), R(1), R(2)$ の値を求める代わりに
- $R(-1), R(0), R(1), R(2), R(∞)$ の値を求める
- ただし、$P(∞)$ $=$ ($P(x)$ の $x^{2}$ の係数)、$Q(∞)$ $=$ ($Q(x)$ の $x^{2}$ の係数) とする
そうすると、連立方程式の答えの分母が最大でも 6 になるので、元の方法よりも実行スピードが (定数倍の面で) 少し高速になります。
3-4. 現在最速!FFT 掛け算
みなさんは「高速フーリエ変換 (FFT)」を知っていますか?知っている読者も知らない読者もいると思います。フーリエ変換は、波のグラフを周波数ごとに分ける変換で、物理など色々な分野に応用されています。
ただしフーリエ変換は、複素数平面など難しい数学の知識を必要とするため、ここでは軽く説明する程度にとどめておきます。
- フーリエ変換を宇宙一分かりやすく解説してみる (フーリエ変換、知りたい!という人向け)
高速フーリエ変換は、長さ $N$ の配列のフーリエ変換11を $O(N \log N)$ の計算時間でやるアルゴリズムです。例えば、以下のようなアルゴリズムが知られています。
-
クーリー=テューキーの FFT アルゴリズム
- 配列の長さ $N$ が $2, 4, 8, 16, …, 2^{k},...$ の場合に、計算時間 $O(N \log N)$ でフーリエ変換するアルゴリズムです。これは 1965 年に発明された、世界初の FFT アルゴリズムです。
-
ブルースタインの FFT アルゴリズム
- 配列の長さ $N$ によらず、計算時間 $O(N \log N)$ でフーリエ変換するアルゴリズムです。レオ・ブルースタインさんが 1968 年に発明しました。
しかし、物理で使うような波の周波数を扱う「FFT」を使うと、全く関係がなさそうに見える N 桁の掛け算の計算が、計算時間 $O(N \log N)$12 でできてしまいます!
3-4-1. FFT と畳み込み
実は、FFT を使うと、配列の「畳み込み」が計算時間 $O(N \log N)$ でできるんです!発展的な内容で難しいので、これは読み飛ばしても構いません。あとで分かりやすい実装例のリンクがあるので、安心してください。
ざっと説明すると、配列 $a = (a_0, a_1, \cdots, a_{N-1})$ と $b = (b_0, b_1, \cdots, b_{N-1})$ は、FFT を使って次のように畳み込みできます。
- 複素数 $w_k = \cos(\pi k / N) + i \times \sin(\pi k / N)$ とする
- 配列 $a$ を長さ $2N$ に伸ばして「高速フーリエ変換」すると、多項式 $P(x) = a_0 + a_1 x + \cdots + a_{N-1} x^{N-1}$ の $x = w_0, w_1, \cdots, w_{2N-1}$ の時の値が求まる
- 配列 $b$ を長さ $2N$ に伸ばして「高速フーリエ変換」すると、多項式 $Q(x) = b_0 + b_1 x + \cdots + b_{N-1} x^{N-1}$ の $x = w_0, w_1, \cdots, w_{2N-1}$ の時の値が求まる
- と 3. の結果を掛け合わせて、$P(x) \times Q(x)$ の $x = w_0, w_1, \cdots, w_{2N-1}$ の時の値が求まる
- $P(x) \times Q(x)$ は $2N-1$ 次多項式なので、4. で求まった $2N$ 個の $x$ の値から「復元」することができる。復元は「高速逆離散フーリエ変換」でできる。
つまり、FFT を 3 回するということです!これで畳み込みができましたね(?)
そもそも FFT ってどういうアルゴリズムなの?とか、FFT はどうやって実装するの?とか思った人は、下の記事を読みましょう。(この部分だけは他の記事に完全に頼りっきりになってしまった…)
2 つの配列を長さが $2^{k}$ になるように伸ばすと、シンプルな「クーリー=テューキーのアルゴリズム」を使えて便利です。この場合は、例えば長さ $100000$ の配列の畳み込みは、長さ $131072 = 2^{17}$ に伸ばして、伸ばした分を 0 で埋めてから、畳み込みをします。
3-4-2. FFT の畳み込みで掛け算!
で説明したように、畳み込みができれば、$N$ 桁の掛け算ができます!
FFT を使うと畳み込みが $O(N \log N)$ で計算できるので、N 桁の掛け算は $O(N \log N)$ で計算できる、という原理です。
例えば、2 つの配列 $(5, 2, 8, 4)$ と $(3, 7, 4, 1)$ を畳み込みすると $(15, 41, 58, 81, 62, 24, 4)$ になります。これに 2-4 節で説明した「繰り上がり処理」を行うことによって、配列が $(5, 2, 2, 7, 0, 1, 7)$ になり、答え「7107225」が分かります。
3-4-3. <発展> 実数を使わずに畳み込み!NTT
(注:この部分は発展編なので、難しいな… と思ったので読み飛ばしても OK です。)
FFT は実数を使うので、桁数が大きくなった時の誤差が怖いですよね?ここで、整数を使って畳み込みをする「NTT(数論変換)」というアルゴリズムの紹介します。
NTT では、FFT でいう複素数 $\cos(\pi/N) + i \times \sin(\pi/N)$ の代わりに「$mod$ $p$ ($p$ は素数) での 1 の $2N$ 乗根」を使って、畳み込みの結果を $mod$ $p$ で求めるアルゴリズムがあります。ここではクーリー=テューキーのアルゴリズムを使うので、$N = 2^{k}$ の形で表されているとします。1 の $N$ 乗根がないような $p$ がほとんどですが、特殊な $p$ を使うことでできます。
長さ $N$ の配列を使うとき、1 の $2N$ 乗根を使うので、素数 $p$ に $2^{k}$ 乗根まである場合、長さ $N$ が $2^{k-1}$ 以下なら畳み込みできます。つまり $2^{k-1}$ 桁までなら正確に動作する、ということです!
比較的大きな $N$ に使える「NTT で便利な素数 $p$ の値」をいくつか書いておきます!
| p の値 (p < 231) | 2k 乗根まで | 2k 乗根の例 (最小) |
|---|---|---|
| 2013265921 = 15 × 227 + 1 | 227 まで | 137 |
| 469762049 = 7 × 226 + 1 | 226 まで | 30 |
| 1811939329 = 27 × 226 + 1 | 226 まで | 136 |
| 167772161 = 5 × 225 + 1 | 225 まで | 17 |
| 1107296257 = 33 × 225 + 1 | 225 まで | 309 |
| 1711276033 = 51 × 225 + 1 | 225 まで | 40 |
| 2113929217 = 63 × 225 + 1 | 225 まで | 551 |
| 754974721 = 45 × 224 + 1 | 224 まで | 362 |
| 1224736769 = 73 × 224 + 1 | 224 まで | 149 |
| 2130706433 = 127 × 224 + 1 | 224 まで | 958 |
また、競技プログラミングで出題される問題で、よく「答えを 998244353 で割った余りを求めてください」というものがありますが、これは素数で $998244353 = 119 \times 2^{23} + 1$ なので、$N \leq 2^{22}$ までなら NTT を使って畳み込みできます。
また、畳み込みの結果が $p$ 以上となってしまう場所がある場合、2 つの $p$ を使って復元することができます。例えば:
- $X$ を $p_1 = 469762049$ で割った余りが $60475902$
- $X$ を $p_2 = 167772161$ で割った余りが $161139195$
この場合、$X = 1000000000$ と "復元" することができます。これは中国剰余定理を使えば、計算時間 $O(\log p)$ で復元できます。この際に $mod$ $p$ での逆元を計算します。
これを使えば、畳み込みの結果が $p$ の値を超える時があっても、2 つの素数 $p$ で NTT を使って計算し、この結果を "復元" すれば解決します。13
「$mod$ $p$ の世界についてもっと知りたい!」という人は、こちらの記事を読むのがおすすめです。$mod$ $p$ の逆元についてだけでなく、$mod$ $p$ での累乗・二項係数・離散対数についてまで詳しく書かれています。
3-4-4. <発展> FFT を使った N1 桁 × N2 桁の掛け算
FFT を使うと、$N = max(N_1, N_2)$ として計算時間 $O(N \times \log N)$ かかるので、例えば $N$ 桁 × 1 桁の掛け算の場合などにおいて、必要以上に時間がかかるのではないか?と思うかもしれません。
しかし、これは改善することができます。例えば、$1234567891234567 \times 8912$ を計算するとして、これをわざわざ「$1234567891234567 \times 0000000000008912$」としなくても良さそうですよね?
この例であれば、$1234 \times 8912$, $5678 \times 8912$, $9123 \times 8912$, $4567 \times 8912$ の「4 桁の掛け算 4 個」に落とし込むことができます。この計算にかかる「log」の部分は、$\log N$ ではなく $\log(\min(N_1, N_2))$ ですから、$N_1$ と $N_2$ の差が大きい場合に速くなっています。
このようにすると、$N_1$ 桁 $\times$ $N_2$ 桁の掛け算を、計算時間 $O(\max(N_1, N_2) \times \log(\min(N_1, N_2)))$ ですることができます。
3-4-5. FFT 掛け算のスピード感
速い実装をすると、現代のコンピューターでは、長さ 100 万の配列の畳み込みを 1 秒程度で実行してくれます。これは、100 万桁の掛け算を 1 秒程度でできることを意味し、筆算ベースのアルゴリズムや、カラツバ法、Toom-Cook 法よりも速いです。
計算時間のオーダーだけでなく、実用上もスピーディーだということを意味しています。私が知る限りでは、FFT 掛け算は、今知られている掛け算のアルゴリズムの中で計算量的にも実用的にも最速です!
しかし、もっと速くしたい!という場合は、1 桁ごとに数を配列で管理するのではなく、5 桁ごととかで数を配列で管理すると、速くなります。例えば、「20151121」を長さ 2 の配列 (51121, 201) で管理する、みたいな感じです。
なぜなら、配列の長さが 1/5 になるからです。ただ、配列の 1 つの値に入れる桁数が多すぎると、オーバーフローしたり、FFT に誤差が生じたり、NTT でやる場合もたくさんの p で計算してから復元する必要が出てきたりするので、このことも考えないといけません。
3-5. ニュートン=ラフソンの割り算アルゴリズム
いま、$N$ 桁の掛け算が $O(N \times \log N)$ の計算時間できるようになりましたね?今のところ、$N$ 桁の四則演算の計算時間はこんな感じです。
| 計算の種類 | N 桁と N 桁 |
|---|---|
| 足し算 | 計算時間 $O(N)$ |
| 引き算 | 計算時間 $O(N)$ |
| 掛け算 | 計算時間 $O(N \log N)$ |
| 割り算 | 計算時間 $O(N^2)$ |
あれれ?割り算だけ遅いですね。これはあまりに不自然です。
もっと速く、計算時間 $O(N \log^{2} N)$ とか $O(N \log N)$ で計算できないでしょうか?
実は、ニュートン=ラフソンの割り算アルゴリズムを使うと、計算時間 $O(N \log N)$ で割り算ができます。
3-5-1. 逆数を精度よく求めれば割り算できる
$A÷B$ を計算することを考えましょう。$1÷B$ ($B$ の逆数) を精度よく求めることさえできれば、これに $A$ を掛けることで求められます。
- 例えば、A = 123456、B = 789 の場合 (123456 ÷ 789 を求める)
- 1÷B = 0.001267427 (精度 7 桁) をなんとかして計算する
- すると、(1÷B) × A = 0.001267427 × 123456 = 156.471467712 と計算できる
- 実際の A÷B は 156.471482889... で、最初の 7 桁が一致している!
つまり、$1÷B$ の値を精度よく求めたら、その分だけの精度で $A÷B$ の値も正確に求まるということです!
小数が出てきたけど、対処できるの?
例えば先ほどの例で出てきた「0.001267427」は、$10^{9}$ 倍すれば「1267427」という整数になるので、整数として計算することができます。先ほどの例での $(1÷B) \times A$ の計算は、$1267427 \times 123456$ を計算すると答えが分かるので、整数の掛け算でできているのが分かると思います。
どのくらいの精度が必要?
$A÷B$ を計算する際に必要な逆数の精度は、($A$ の桁数) ÷ ($B$ の桁数) + 1 桁程度です。
これは、逆数 $1÷B$ を小数第 ($B$ の桁数) 位くらいまで求めるとよい、ということです!
逆数がこの精度で求まれば、(求めた $1÷B$) $\times A$ の計算は、$N$ 桁の掛け算なので計算時間 $O(N \log N)$ でできます。だから、もし逆数 $1÷B$ が計算時間 $O(N \log N)$ で求められるならば、$A÷B$ の商は $O(N \log N)$ で求まるでしょう。
うまくいかない場合もあるのでは?
例えば、$9149999 ÷ 1177$ を計算することを考えましょう。この場合:
- 逆数 1÷1177 を精度 4 桁で求めて、これ以下を切り捨てると「0.0008496」
- このとき、(求めた 1÷1177 の値) × 9149999 は 0.0008496 × 9149999 = 7773.8391504
- これで「9149999 ÷ 1177」の商は 7773 と求まるが、実際は 7774
この場合は答えが 1 だけ下にずれています。これはマズい、と思うかもしれません。
しかし、どんな場合でも答えが 1 までしか下にずれない14ので、この例の場合では答えが 7773 または 7774 であることが確定します。このどちらであるかの判定は:
- 「9149999 は、1177 × 7774 以上ですか?」 → YES なので、答えは「7774」と分かる
こんな感じでできます。
判定は $N$ 桁オーダーの掛け算を 1 回するだけなので、追加で計算時間 $O(N \log N)$ しかかかりません。
3-5-2. 逆数を効率的に求めたい!
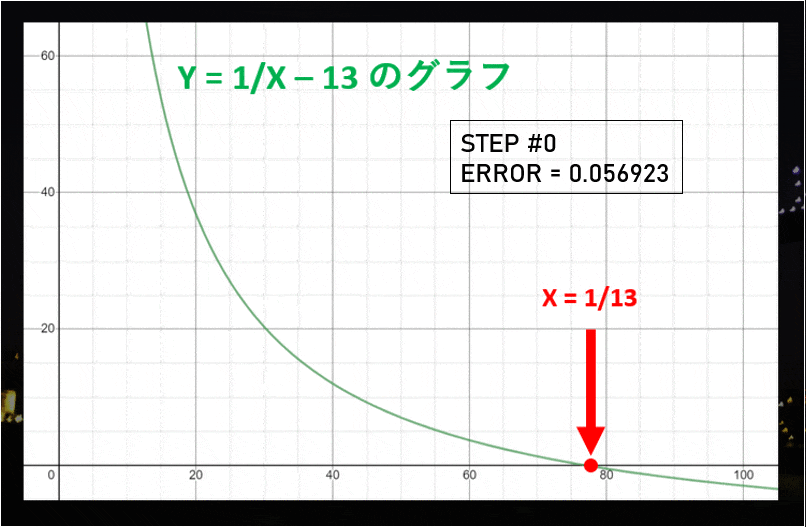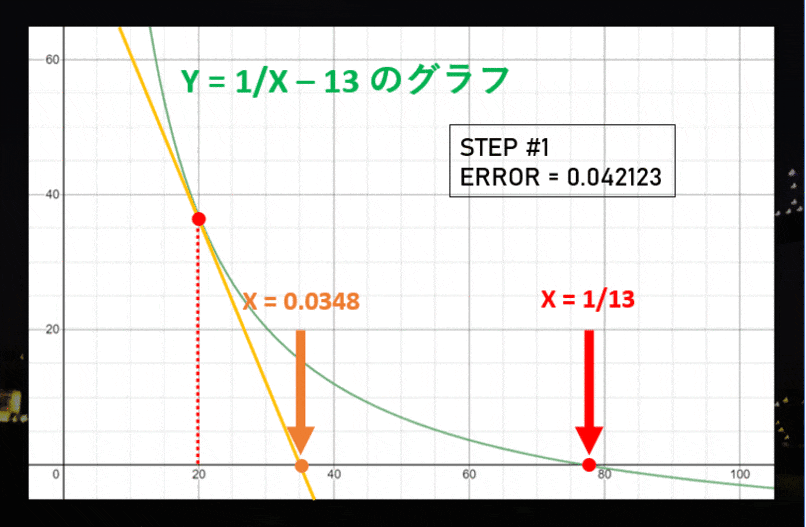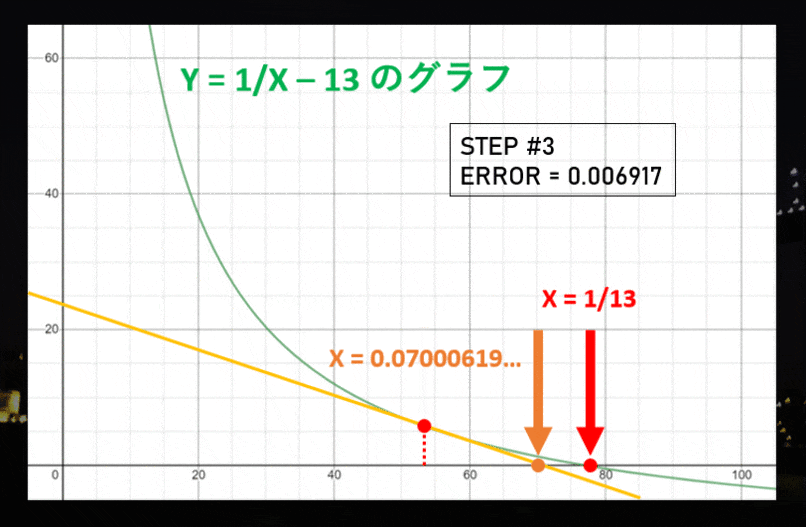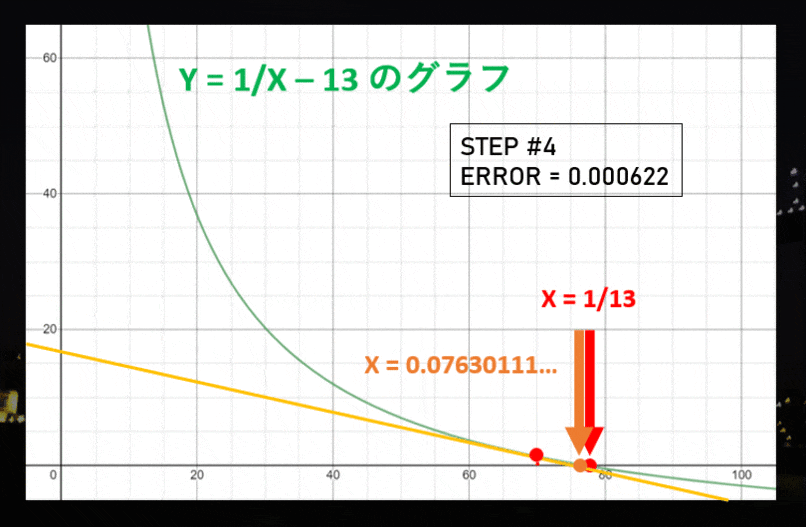
ここで、$Y = 1/X - B$ のグラフを考えましょう。このグラフと X 軸との交点 ($Y = 0$ となる X の値) は「$X = 1/B$」つまり「B の逆数」になっていると思います。
例えば、$B = 13$ の場合、グラフは次のようになります。 (表示の都合上 X 軸を 1,000 倍しています)
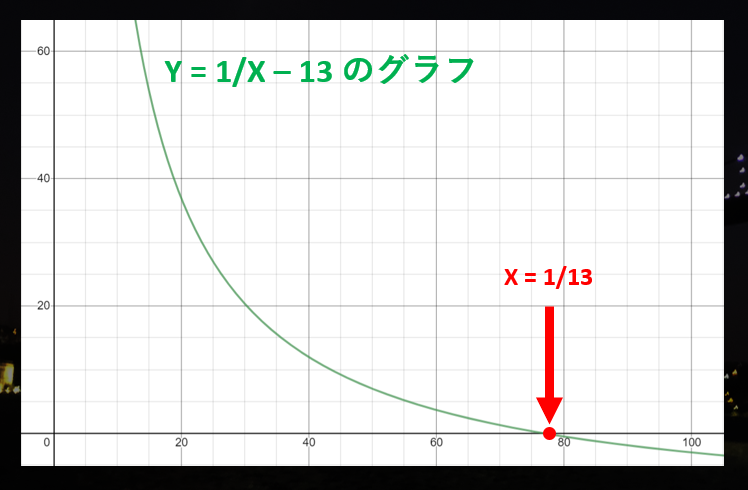
ステップ 0
ここで例えば、大ざっぱに「$1/13$ は大体 $0.02$ になるな!」と予想を付けることにしましょう。
ステップ 1
ただし、実際の $1/13$ の逆数は、$0.02$ より少し大きいですよね?だから、グラフの $X = 0.02$ の部分に接する直線を引いてみると、X 軸との交点は元々よりも「本当の値に近い」位置になってるはずです!
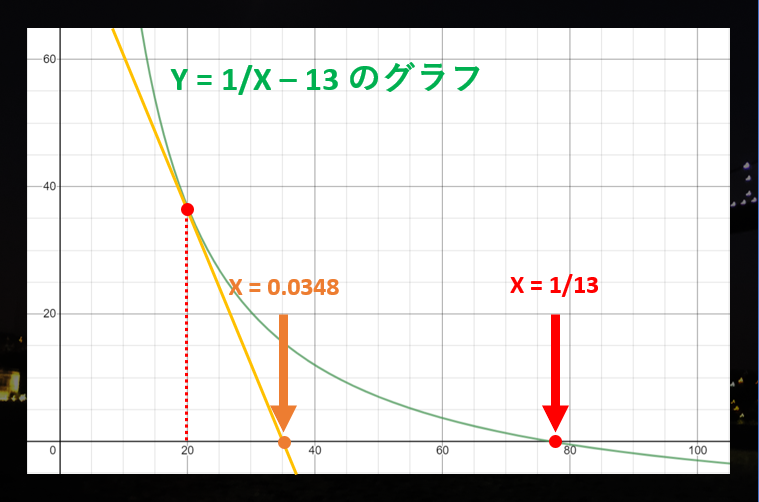
これで、新たな予想「$1/13$ は大体 $0.0348$ になるな!」が立ちました。
ステップ 2
これは前の予想よりも本当の値に近くなっていますが、まだまだです。さっきと同じように、グラフの $X = 0.0348$ の部分に接する直線を引いてみると、X 軸との交点は元々よりも「本当の値に近い」位置になってるはずです!
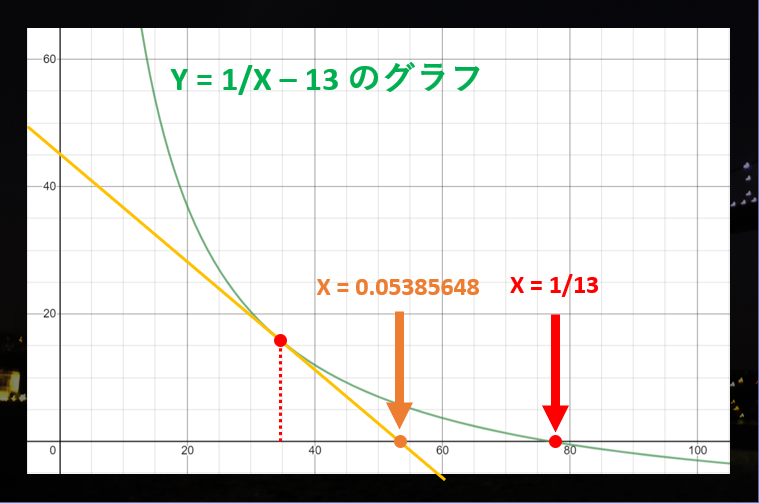
これで「新たな予想「$1/13$ は大体 $0.05385648$ になるな!」が立ちました。これは前の予想よりも本当の値に近くなっていますが、まだまだです。ステップ #3 以降は、こんな感じで進んでいきます。
本当の値に近くなればなるほど速いペースで近づいてるのが分かると思います。
実際に、$X = 0.02$ を初期値にした場合、次の 7 ステップではこんな感じになります。
| ステップ数 | X の値 | 精度 |
|---|---|---|
| 初期値 | 0.02 | 0 桁 |
| 1 回終了 | 0.0348 | 0 桁 |
| 2 回終了 | 0.05385648 | 0 桁 |
| 3 回終了 | 0.0700061943061248 | 1 桁 |
| 4 回終了 | 0.07630111447629989521944768872448... | 2 桁 |
| 5 回終了 | 0.07691804803836931180318924405574... | 3 桁 |
| 6 回終了 | 0.07692307659431106484511823745278... | 8 桁 |
| 7 回終了 | 0.07692307692307692167179221291744... | 16 桁 |
| 8 回終了 | 0.07692307692307692307692307692307... | 32 桁 |
本当の値は 1/13 = 0.0769230769230... です。これと一致する桁数は、3 ステップ目の終了で初めて 1 桁になりますが、ここからは一致する桁数が 1 ステップで約 2 倍ずつ増えていきます。
つまり、逆数を $N$ 桁の精度で求めるのに、大体 $\log N$ ステップしか掛からないんです!
3-5-3. 「次のステップの逆数の予測値」の出し方
どんな感じで動いてるのかが分かりましたね?しかし、「$0.02$ から次の予測値は $0.0348$」「$0.0348$ から次の予測値は $0.05385648$」などという具体的な数値は、どのようにして計算するのでしょうか?
まず、$Y = 1/X - B$ のグラフ上の、$X = a$ の場所に接する直線の傾きは、$-1/a^{2}$ であることが知られています15。例えばグラフの $X = 0.02$ の場所に接する直線の傾きは $-2500$ です。
ここで、グラフの $X = a$ の場所の座標は、$(a, 1/a - B)$ となっています。この Y 座標 $1/a - B$ から、$1/a^{2}$ のペースで直線がグラフを降りていくと、X 座標はいくつ増えるでしょうか?
答えは、$(1/a - B) \times a^{2} = a - b \times a^{2}$ です。例えば、$a = 0.02, B = 13$ の場合、計算すると X 座標が元より 0.0148 増えることになります。だから、新しい予測値は
$$a + (a + B \times a^{2}) = a × (2 - B \times a)$$
になる、ということです!
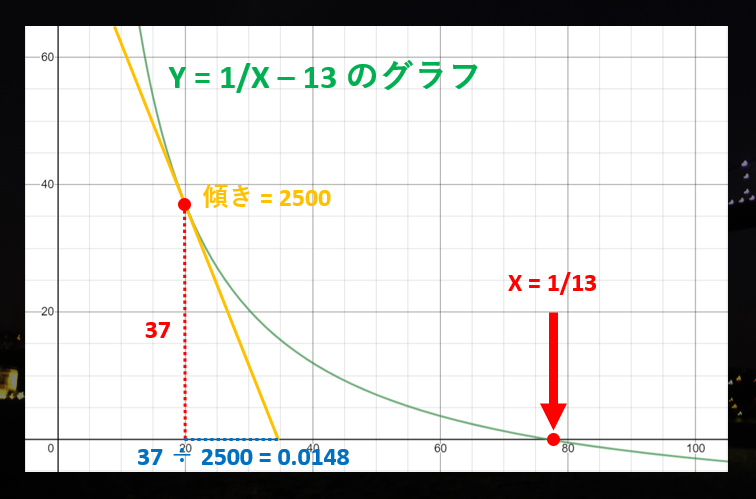
つまり、元の予測値が $X$ の場合、**新しい予測値は「$X × (2 - B \times X)$」で計算できます!**この式に当てはめると、先ほどの表の $X$ の予測値が正しく計算されていることが分かると思います。
よく見てください。なんと驚くべきことに、これは引き算と掛け算だけで実現されています。なんと上手いことか、**この方法では「割り算を使わずに逆数を求められる」**のです!
3-5-4. 計算時間はどのくらい?
次のよう $B$ の桁数で初期値を決定すれば、逆数 $1÷B$ の初期値は誤差 10 倍以内にできます。
- $1 \leq B \leq 9$ の場合、逆数の初期値は 0.1
- $10 \leq B \leq 99$ の場合、逆数の初期値は 0.01
- $100 \leq B \leq 999$ の場合、逆数の初期値は 0.001
- $1000 \leq B \leq 9999$ の場合、逆数の初期値は 0.0001
- ... (後略)
このようにすると、数ステップ目以降からどんどん一致する桁数が 2 倍ずつ増えていきます。したがって、精度 $N$ 桁で計算する場合は、ステップが $\log N$ 回程度になります。
また、$X$ は精度 $N$ 桁で計算すればよいので、各ステップで「$N$ 桁の掛け算 2 回と $N$ 桁の引き算を 1 回」をします。だから、各ステップにかかる計算時間は $O(N \log N)$ です。
したがって、計算時間 $O(N \log^{2} N)$ で、逆数 $1÷B$ が精度 $N$ 桁で計算できますね。
3-5-1 節で書いたように、逆数が精度 $N$ 桁で求められれば $N$ 桁の割り算ができますから、この方法で **N 桁の割り算は $O(N \log^{2} N)$ で計算できます。**筆算の $O(N^{2})$ に比べたら圧倒的成長です!現代の技術は素晴らしいですね。
3-5-5. 少しの工夫でさらに高速化!
実は、ほんの少しの工夫だけで、計算量 $O(N \log N)$ に高速化できます!
例えば、精度 100 万桁で逆数を求めたいとしましょう。この時、最初の数ステップでは、100 万桁も記録する必要なんてありませんよね?この時点での精度が 10 桁もない状況で、100 万桁の計算を行っても計算時間の無駄です。
だから、計算途中の $X$ の精度を、各ステップで桁数にして 2 倍ずつ上げていこうではありませんか!
1 桁が一致した状態からだと、これから一致桁数が 1 → 2 → 4 → 8 → 16 → … と 2 倍ずつ増えていくことが予想されるので、その時点からは「$X$ の計算精度」の桁数を 2 倍ずつ増やします。
つまり、こんな感じで計算していきます!この例は、初期値 $X = 0.03$ で $1/13$ を計算するときです。
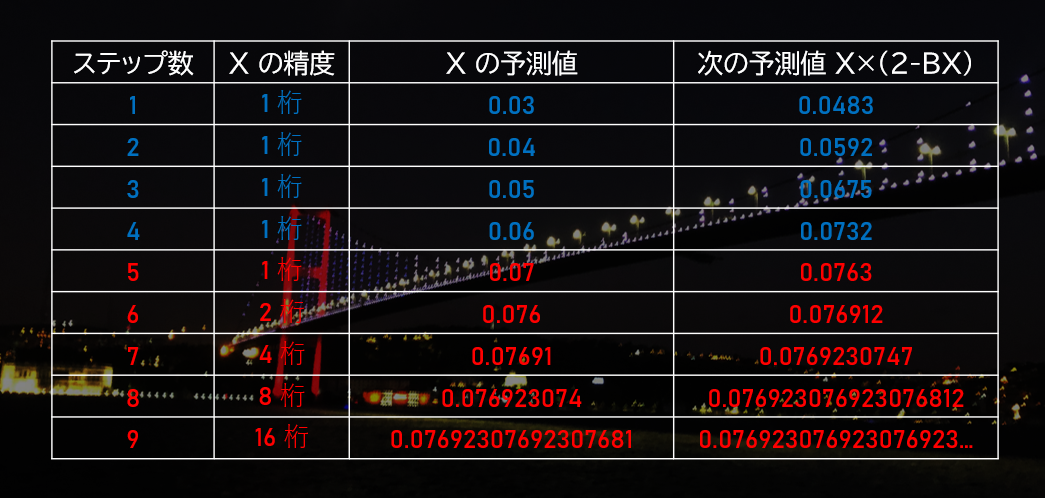
これで計算回数は、$O(1 \times \log(1) + 2 \times \log(2) + 4 \times \log(4) + 8 \times \log(8) + ... + N \times \log(N))$ みたいにになって、これは $O(N \log N)$ です。だから、逆数を精度 $N$ 桁で求めるのは、$O(N \log N)$ で計算できます!!!
これで、N 桁の割り算も $O(N \log N)$ で計算できる、ということなんです。
3-5-6. あまりの計算
ここまでで、N 桁の割り算の商が $O(N \log N)$ で計算できました。しかしニュートン=ラフソンの割り算アルゴリズムは、筆算とは違って商とあまりを同時に求めているわけではありません。
でも、商が求まれば、あまりは求まります。例えば、$123456 ÷ 789$ の商が $156$ であることが分かっているとしましょう。この時、あまりはいくつになるでしょうか?
これは「$123456$ 個の中で、$789×156$ 個から "余らされた" ものの個数」と考えることができるので、**あまりは「$123456 - 789×156 = 372$」**と計算ができます。
このようにすれば、商が分かっていれば、あまりは 1 回の掛け算と引き算で求まります。掛け算の計算量は $O(N \log N)$ ですから、結局あまりも商と同じ計算時間オーダー $O(N \log N)$ で計算できました。16
3-6. ゴールドシュミットの割り算アルゴリズム
3-6 節では、ゴールドシュミットの割り算アルゴリズムについて説明します。1964 年にロバート・ゴールドシュミットさんが発明したことから、このように名づけられています。現代でも CPU プロセッサー上での割り算の計算に使われていることもあります。
計算量は $O(N \log^{2} N)$ でニュートン=ラフソンの割り算アルゴリズムより遅いですが、けっこうシンプルで分かりやすいので紹介します。
3-6-1. 「123456 ÷ 789 → ?????? ÷ 1000」
もし、$123456 ÷ 789$ が「$?????? ÷ 1000$」の形で表されれば、この $??????$ の値を使って割り算の商を計算することができます。完全に正確とはいえませんが、これが「$156471 ÷ 1000$」と表されるならば、この商は 156 だと分かると思います。
ゴールドシュミットの割り算では、**"なんとかしてでも" こういう上手い形にしたいと思います。このために、分子と分母に同じ数を掛け算します。**どのくらい掛け算すればいいのか考えてみましょう。
ステップ 1
0.789 の 1 について対称な位置は 1.211 です。だから、0.789 × 1.211 は 1 に近くなりそうですね?だから、分子と分母に 1.211 を掛け算してみましょう。実際にやってみるとこんな感じです。
- 分子は 123456×1.211 ≒ 149505 になり、分母は 789×1.211 ≒ 955 になる。
- すると、現時点での割り算は「149505 ÷ 955」です。
ステップ 2
0.955 の 1 について対称な位置は 1.045 です。だから、0.955 × 1.045 は 1 に近くなりそうですね?だから、分子と分母に 1.045 を掛け算してみましょう。実際にやってみるとこんな感じです。
- 分子は 149505×1.211 ≒ 156232 になり、分母は 955×1.045 ≒ 997 になる。
- すると、現時点での割り算は「156232 ÷ 997」です。
結果
もう 2 回目の時点で、分母が「997」と 1000 とほとんど同じになりました。とても速いです!
$N$ 桁の割り算をするとき、各ステップは分母と分子に $N$ 桁くらいの数を掛けるので計算時間は $O(N \log N)$ になります。このステップを $\log N$ 回程度繰り返すと "上手い形" が出来上がります。
よって、この方法だと $N$ 桁の割り算を $O(N \log^{2} N)$で計算できます。
3-6-2. 必要なステップ数はどのくらい?
かりに分母が小数で表されて、これが $x \ (0 < x < 1)$ のときを考えましょう。この分母をゴールドシュミットの割り算で "なんとかして" 1 にしようとします。分母に $2-x$ を掛けると…?
$$x \times (2-x) = -x^2 + 2x = 1 - (1-x)^2$$
つまり、$x$ の「1 との差」が 2 乗されているということです!例えば $x = 0.6$ の時、「1 との差」は 0.4 ですが、ステップを終えると分母は 0.84 になっています。これの「1 との差」は 0.4² = 0.16 ですね?そういうことです。
次のステップでさらに「1 との差」は 2 乗され、その次のステップでも「1 との差」は 2 乗され… これが繰り返されます。「1 との差」が 2 乗されるというのは、精度の桁数が 2 倍になるということです。N 桁の割り算では、精度を $N$ 桁オーダーにする必要がありますから、$\log N$ ステップ程度かかります。
みなさん、ゴールドシュミットの割り算を理解できましたか?
私にとっては「けっこうシンプルだけど方法が面白いなあ」と感じました。
3-7. ここまでのまとめ
これで第 3 章「理論編」はおしまいです。お疲れ様でした!
ここで説明した N 桁の掛け算・割り算のアルゴリズムは、次の通りです!
| アルゴリズム | 種類 | 計算時間 | (参考) 英語名 |
|---|---|---|---|
| カラツバ法 | 掛け算 | $O(N^{1.59})$ | Karatsuba's Algorithm |
| Toom-Cook-3 法 | 掛け算 | $O(N^{1.47})$ | Toom-Cook-3 Algorithm17 |
| FFT 掛け算 | 掛け算 | $O(N \log N)$ | FFT-based Multiplication |
| NTT 掛け算 | 掛け算 | $O(N \log N)$ | NTT-based Multiplication 18 |
| ニュートン=ラフソン法 | 割り算 | $O(N \log N)$ | Newton-Raphson Division |
| ゴールドシュミット法 | 割り算 | $O(N \log^{2} N)$ | Goldschmidt Division |
また、$N_1$ 桁 $\times$ $N_2$ 桁の掛け算は、FFT 掛け算を少し工夫することで、$O(\max(N_1, N_2) \times \log(\min(N_1, N_2)))$ で計算できるようになります。
こんな感じです。掛け算も割り算も $O(N \log(N))$ でできてしまいました!
これを使いこなせるとめっちゃ強いです!例えば、$\sqrt{2} = 1.4142…$ や円周率 $\pi = 3.1415…$ の小数点以下の値が高速に求められるだけでなく… 4 章を楽しみにしておいてください。
実装したプログラムを AOJ で確認しよう!
多倍長整数を実装して、プログラムを確認したい!と思う時があるかもしれません。
ここでおすすめのサイトを紹介します。**「会津大学オンラインジャッジ (AOJ)」**という、会津大学が管理している競技プログラミングの練習サイトがあります。
これは「コース」と「チャレンジ」の 2 種類に分かれていて:
- コース:プログラミングの初歩的な問題 (Introduction to Programming) や、典型アルゴリズムの問題が用意されている。プログラムを提出すると自動採点される。
- チャレンジ:日本情報オリンピックなどの競技プログラミングの大会で出題された問題のジャッジが用意されている。プログラムを提出すると自動採点される。解いた問題数のランキングもある。
なんと、**「コース」**に多倍長整数のジャッジが用意されています!
NTL-2「多倍長整数」 です。実装して自動採点されたい!とか、結果を確認したい!という人は、このジャッジにあなたが書いたプログラムを提出するといいと思います。
多倍長整数を自分で実装できれば、あとは第 4 章で扱う √2 や円周率 π の小数点以下が高速に求められたりなど、いろんなことができます。みなさんもぜひ多倍長整数を自分でも実装してみて、AOJ にプログラムを提出してみましょう!
多倍長整数以外にも色々なアルゴリズムを実装したい!という人は、「コース」の他の問題を解いてみるのもいいですし、プログラミングやアルゴリズムを使った面白い問題を解いてみたい!という人は、AOJ の「チャレンジ」で情報オリンピックなどの問題に挑戦してみてもいいかもしれません…!
つづく
第 4 章「応用編」に続きます。
いま、掛け算・割り算を $O(N \log N)$ で計算する方法を獲得しました。次の章では、この圧倒的なスピードを使いこなしていきます!
後編(第 4 章)も是非ご覧ください!
-
1 回のループで足される数が最大 9×9=81 で、これが約 2600 万回重なれば、int 型 (32 ビットの整数型) をオーバーフローします。計算時間的にあまり現実的でないと思いますが、万が一「掛け算する 2 つの数がともに 2600 万桁以上になる」ことがある場合は 64 ビット整数型を使うなど工夫するといいと思います。 ↩
-
厳密な意味だと「離散畳み込み」です。もうひとつは難しいですが、連続関数を積分で畳み込みする「連続畳み込み」もあります。本記事では解説しませんが、気になる人は調べてみましょう。 ↩
-
必要な #include は済ませておきましょう。#include , #include , #include , #include が必要です。 ↩
-
コルモゴロフは、「ヒルベルトの第 13 問題」を解決したことなどで知られています。 ↩
-
N/2+1 桁になる場合もありますが、オーダーの意味では同じです。1 桁は誤差のようなものなので、計算時間を見積もる際にはあまり関係がありません。 ↩
-
2~3 桁になることもあります。桁をちょうど 2 等分する実装では、減り方が 1024 → 513 → 258 → 130 → 66 → 34 → 18 → 10 → 6 → 4 → 3 桁、になるのが最悪の場合です。この場合でも、普通の掛け算を使って、定数時間で (つまり一瞬で) 計算することができます。 ↩
-
番号 k のマスの下にある 3 頂点の番号 l, l+1, l+2 を計算時間 O(1) で返す関数を作ると、実装がしやすいです。これはステップ #2 でも同じです。 ↩ ↩2
-
N÷3 桁の掛け算 5 つに落とし込む前に、O(N) かかる計算をを数十回しなければならず、N÷3 桁の掛け算 5 つに落とし込んだ後も、O(N) かかる計算を数十回する必要があります。したがって、計算時間の定数倍は非常に大きく、実用的な速度ではカラツバ法とあまり変わらないでしょう。 ↩
-
これは「Toom-3 法」とも呼ばれます。「Toom-Cook 法」は、後ほど解説する 4 分割, 5 分割,… の場合も含めたときの呼び方です。 ↩
-
$a_6 x^6 + a_5 x^5 + a_4 x^4 + a_3 x^3 + a_2 x^2 + a_1 x^1 + a_0$ で表される式のことです。 ↩
-
厳密な意味だと、ここでは離散フーリエ変換を指しています。これは、波の単位周期 2π を N 等分した x での波の座標が入力されたときに、周期 2π, 2π/2, 2π/3,..., 2π/N の波の大きさに変換するものです。連続関数を積分を使ってフーリエ変換する「連続フーリエ変換」もあります。 ↩
-
この計算時間は、コンピューターの bit 数 (例えば、32 bit のパソコン、64 bit のパソコン) を B、コンピューターのメモリサイズを S とするとき、2B が S に応じて動くという現代のコンピューターモデルを仮定しています。FFT する配列の長さ N は普通に考えると S 以下になりますが、FFT の結果の実数 (double 型など) の精度は B ビット程度あると考えてよいので、うまくいきます!このコンピューターモデルを仮定しなければ、N が無限に大きくなる場合、FFT 系のアルゴリズムを用いた N 桁の掛け算の計算時間は O(N × log(N) × log(log(N))) になるとされています。 ↩
-
実際に高速な「大きな数の計算」を実装したいときは、1 桁ごとではなくて 5 桁ごととかで数を配列で管理します。この際には畳み込みの結果が $p_1 \times p_2$ も超えることがあり、2 つの素数を使っても復元できない場合があります。この場合は 3 つの素数を使って畳み込みを計算し、これを復元すればよいです。 ↩
-
これは「逆数の精度 N 桁より下を切り捨てた値」が正確に求まった場合の話です。もう少し誤差のある値が逆数として求まれば、ずれが 1 より大きくなる場合が出てきます。 ↩
-
高校 2~3 年生の数学で習う「微分」を知っておくと理由が分かります。「Y = 1/X - B」を X で微分すると、「Y' = -1/X²」になります。これは、グラフ上の X = a の部分に接する直線の傾きが -1/a² であることを意味しています。 ↩
-
逆に、あまりが分かっている状態で商を復元するのは、足し算・引き算・掛け算だけでは難しいです。 ↩
-
より一般的には「Toom-3 Algorithm」あるいは「Toom-Cook 3-way Multiplication Algorithm」などの呼び方が使われています。 ↩
-
NTT は「Number Theoretic Transform」の略です。また、NTT 掛け算の一種として「シューンハーゲ・シュトラッセンのアルゴリズム」(Schönhage–Strassen Algorithm) があります。 ↩