0. はじめに
からの続きです!!
後編は第 4 章「多倍長整数演算 ~応用編~」です。
第 3 章で、$N$ 桁の数の掛け算・割り算を計算時間 $O(N \log N)$ でやる方法を手に入れたので、これを利用していろいろなものを効率的に計算していきたいと思います!
目次
第 1 章:はじめに ~メインを読むための準備~
| 章 | タイトル | 備考 |
|---|---|---|
| 1-1. | 人間の計算速度はどのくらい? | |
| 1-2. | コンピューターの計算速度はどのくらい? | |
| 1-3. | 計算回数をかぞえてみよう | 計算時間について扱います |
第 2 章:多倍長整数演算 ~初級編~
| 章 | タイトル | 備考 |
|---|---|---|
| 2-1. | プログラミングでも大きな数を扱いたい! | 大きな数の実装、スタート! |
| 2-2. | 大きな数の足し算 | |
| 2-3. | 大きな数の引き算 | |
| 2-4. | 繰り上がり処理 | 単純な実装には欠かせない! |
| 2-5. | 大きな数の掛け算 | |
| 2-6. | 大きな数の割り算 | |
| 2-7. | ここまでのまとめ |
第 3 章:多倍長整数演算 ~理論編~
| 章 | タイトル | 備考 |
|---|---|---|
| 3-1. | 1960 年 ~すべての始まり~ | |
| 3-2. | 画期的な掛け算の方法、カラツバ法! | 意外とシンプルです |
| 3-3. | さらに速い、Toom-Cook 法! | |
| 3-4. | 現在最速!FFT 掛け算 | 計算時間 O(N × log(N)) |
| 3-5. | ニュートン=ラフソンの割り算アルゴリズム | 計算時間 O(N × log(N)) |
| 3-6. | ゴールドシュミットの割り算アルゴリズム | O(N × log²(N)) だけど手軽! |
| 3-7. | ここまでのまとめ |
第 4 章:多倍長整数演算 ~応用編~
| 章 | タイトル | 備考 |
|---|---|---|
| 4-1. | N! の高速な計算 | 感動的なアルゴリズムかも? |
| 4-2. | √2 を精度よく求めよう | ここにもニュートン法が登場! |
| 4-3. | 円周率 100 万桁に挑戦! | |
| 4-4. | Constants コンテストへのいざない | |
| 4-5. | 大きな数を使った面白い問題の紹介 | |
| 5. | おわりに |
4-0. ここまでのおさらい
N 桁の足し算・引き算・掛け算・割り算は、最速で次の計算時間でできます!
第 4 章を読む上で、これだけは分かってください。
| 計算の種類 | 計算時間 | (参考) 最速アルゴリズム |
|---|---|---|
| 足し算 | $O(N)$ | 筆算 |
| 引き算 | $O(N)$ | 筆算 |
| 掛け算 | $O(N \log N)$ | FFT 掛け算 |
| 割り算 | $O(N \log N)$ | ニュートン=ラフソン法 |
4-1. N! の高速な計算
$N! = 1 \times 2 \times 3 \times 4 \times \cdots \times N$ を計算してみましょう。
$N!$ は場合の数を求める問題でよく出てきて、こんな感じのものが求まります。
- $1, 2, ..., N$ が書かれたトランプのカードが 1 枚ずつあるとき、これを一列に並べる順番は何通りあるか?
例えば、$N = 13$ の場合 $13! = 6,227,020,800$ 通り、のように計算できます。
また、$N!$ は二項係数 $_NC_K$ を求めるのにも使われます。
$N!$ が求まれば、$_NC_K = N! \div K! \div (N-K)!$ で掛け算・割り算するだけで計算できますね。
- $N$ 個の区別できるボールから $K$ 個を選ぶ方法は何通りか?
これが $_NC_K$ になります。例えば、$N = 7, K = 3$ の場合「35 通り」です。パスカルの三角形に出てくることで知っている人も多いかと思います。
だから $N!$ の計算は、色々なタイプの「何通りあるか数え上げる」問題、いわゆる数え上げ問題の答えを求めるのに便利になってきます。もっと数え上げ問題について知りたい!って人はこれを読みましょう。
4-1-1. N! は普通に求めると時間がかかる!
第 3 章で、掛け算を $O(N \log N)$ で計算できる方法を手に入れました。
例えば、$N!$ を $1×2 = 2, 2×3 = 6, 6×4 = 24, 24×5 = 120, 120×6 = 720$,… という感じで計算すると…?

この時の計算時間はどのくらいになっているのでしょうか?$K$ 回目のステップでは $(K-1)!$ に $K$ を掛け算していますが、$K!$ の桁数は大体 $K \times \log_{10}K$ 程度です。
だから各ステップは、($K \times \log_{10}K$ 桁くらい) × ($\log_{10}K$ 桁くらい) の掛け算になります。すると、1 ステップの計算時間は $O(K \log^{2} K)$ になります。
だから、残念なことに、$N!$ を求めるのに計算時間 $O(N^{2} \log^{2} N)$ もかけているのです…
普通の筆算でも FFT でもほとんど計算時間が変わらないのが分かるでしょう。そうなんです、従来の計算方法では、**FFT 掛け算のスピードが全く生かせていない**のです。
このままだと、$100000!$ を求めるだけでも、数十分という長い時間がかかることになって大変です。今回は**「分割統治法」**というアイデアを使って、FFT 掛け算のスピードを生かして高速に $N!$ を計算します。
4-1-2. FFT 掛け算のスピードを生かすために
FFT 掛け算は「2 つの数の桁数」が近い時に、筆算に比べて強さを発揮します。例えば 100 万桁 × 数十桁の掛け算だと、筆算と FFT 掛け算がほぼ同じスピードになりますが、100 万桁 × 100 万桁の掛け算だと FFT 掛け算の方が数万倍速いのは想像に難くないことでしょう。
でも N! の計算過程では、「100 万桁 × 数桁」のような FFT のスピードが全く生かせていない計算をたくさんやっています。どうりで速くならないわけです。
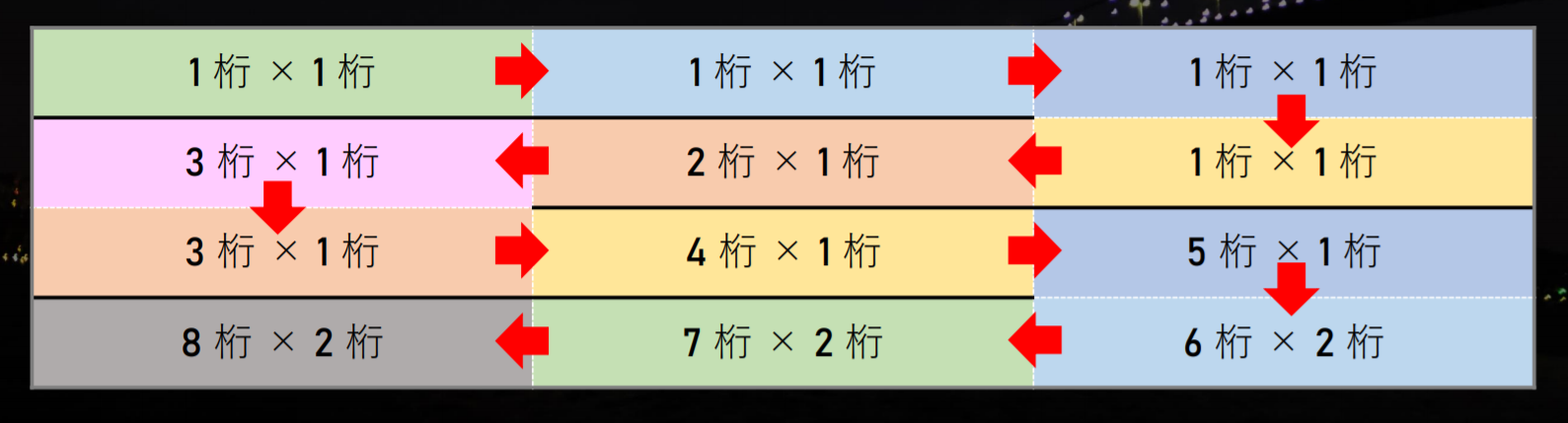
上の図を見ると、まさに絶望的な光景が広がっています。しかし、桁数をできるだけそろえるために、計算のやり方をちょっと変えてみましょう。
例えば、$16!$ の計算方法をちょっと変えて、こんな感じで計算してみましょう。
- 1×3×5×7×9×11×13×15 = 2027025 を頑張って計算する
- 2×4×6×8×10×12×14×16 = 10321920 を頑張って計算する
- すると、$16!$ は 2027025 × 10321920 で計算できる!
ここで、最後の掛け算は「7 桁 × 8 桁」になっています。ほとんどそろっていますね!
最後は $O($桁数 $\times$ $\log($桁数$))$ の計算時間でできているので、FFT 掛け算のスピードが生かせています。
こんな感じの工夫を至る所でやっていくことで、計算時間が大幅に短くなりそうですね!
4-1-3. 至る所で桁数をそろえよう
先ほど、奇数のグループと偶数のグループに分けて計算しましたが、例えば $100000!$ を求める時
- 1×3×5×7×9×…×99997×99999 と 2×4×6×8×10×…×99998×100000 を求める必要がある!
大きなスケールだと、それぞれを計算するのにも長い時間がかかるのが分かるでしょう。
ただ、これに長い時間がかかっているのは、FFT の掛け算のスピードが生かせていないからです。
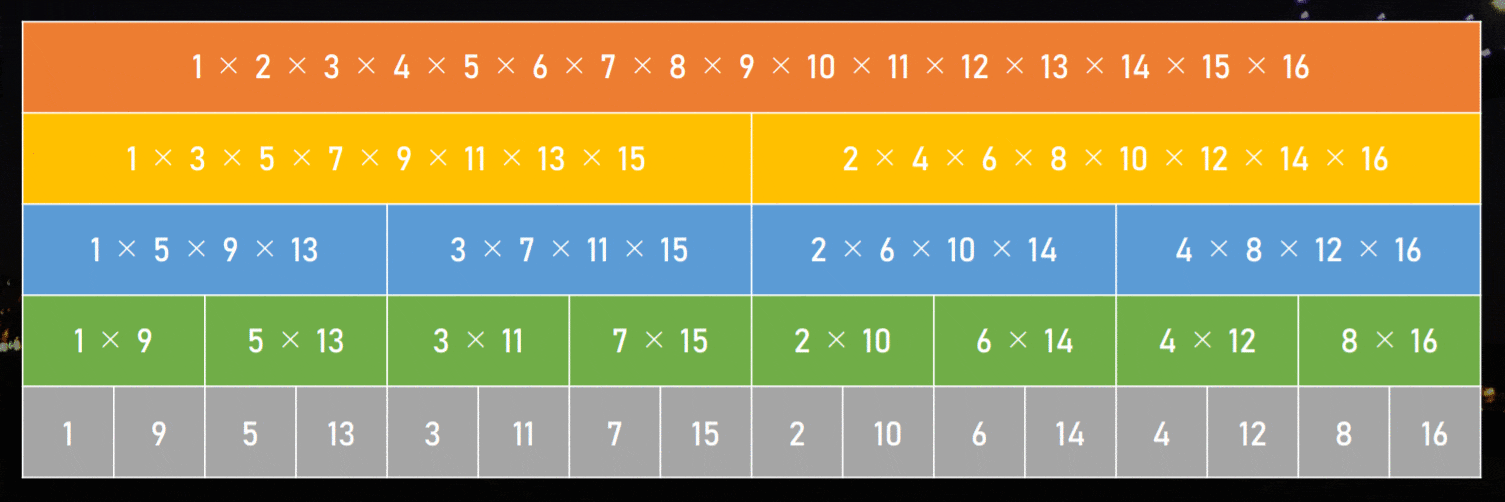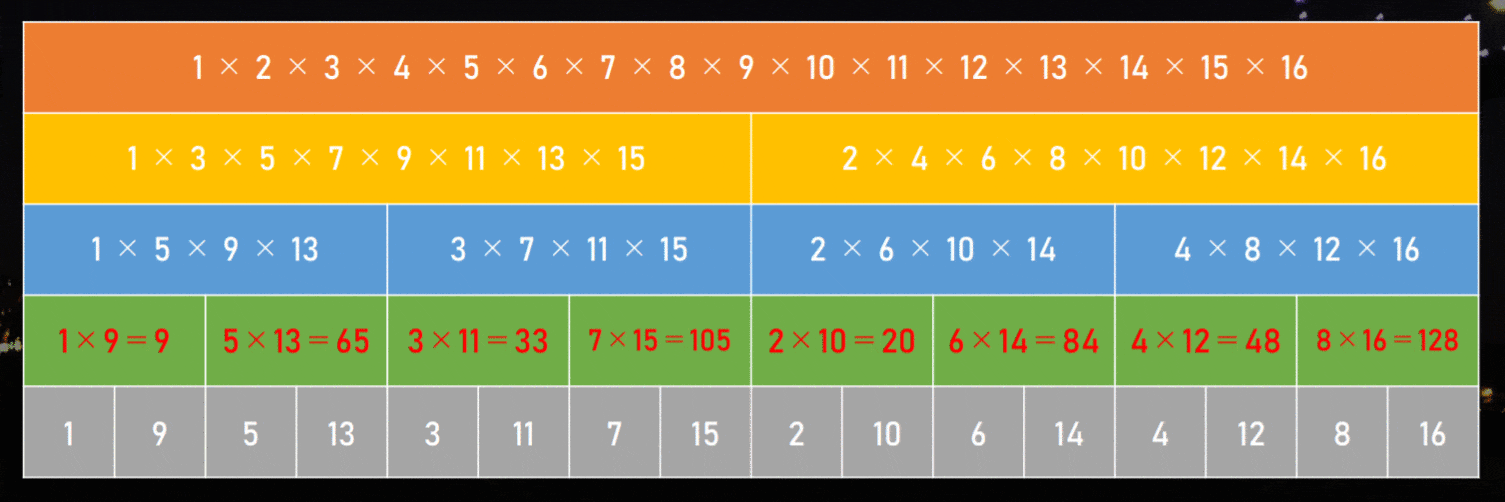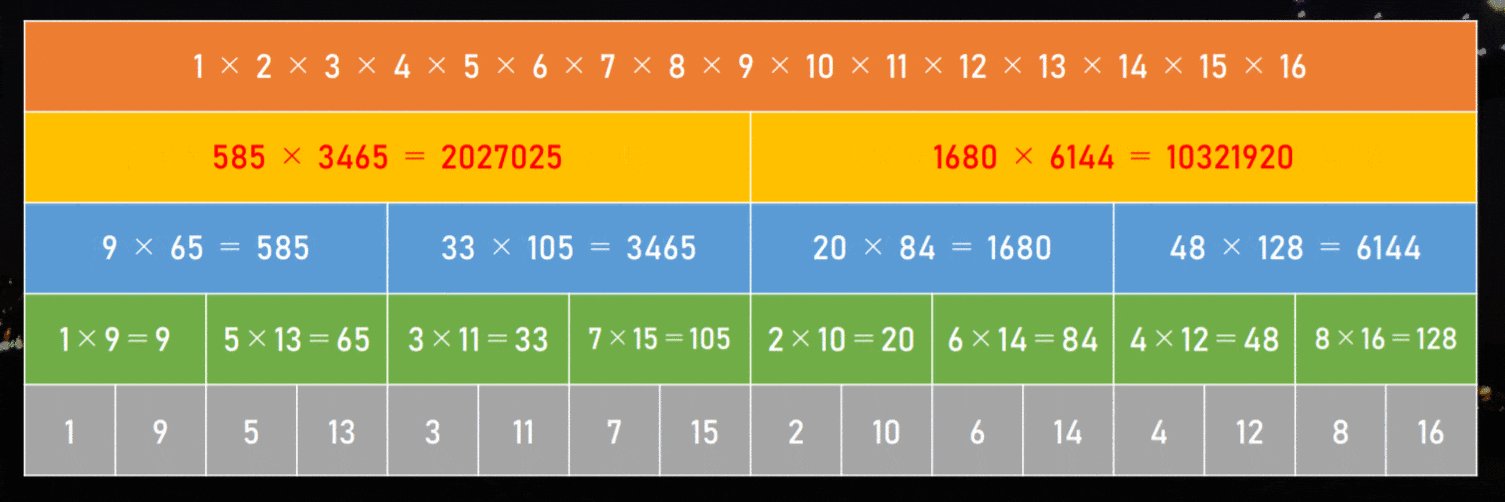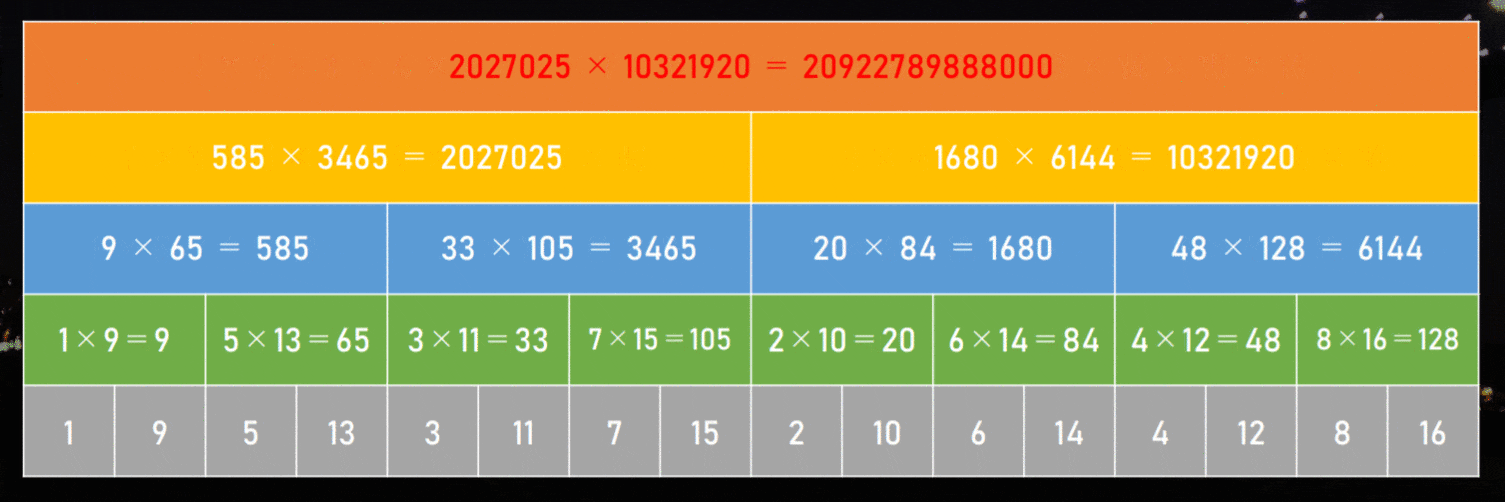
ここで、例えば 1×3×5×7×9×…×99997×99999 を計算する時にも、掛け算の桁数を可能な限りそろえる工夫ができるんです!
- 1×5×9×13×17×…×99993×99997 を計算する (この結果を A とする)
- 3×7×11×15×19×…×99995×99999 を計算する (この結果を B とする)
- すると、1×3×5×7×9×…×99997×99999 = A × B で計算でき、桁数がそろっているので速い!
この工夫を至るところでやると、こんな感じになります。
明らかに速くなりそうなのが一目瞭然だと思います!
4-1-4. 計算時間はどのくらい?
例えば、$64!$ の計算では、次の計算を順にやっています。FFT 掛け算の計算時間が $O(N \log N)$ なので、計算回数 (目安) は $N \log N$ で見積もっています。1
| 下からの段数 | 計算内容 | 計算回数 (目安) |
|---|---|---|
| 下から 2 層目 | 「2 桁以下の掛け算」× 32 回 | 64.0000 |
| 下から 3 層目 | 「4 桁以下の掛け算」× 16 回 | 128.0000 |
| 下から 4 層目 | 「7 桁以下の掛け算」× 8 回 | 157.2119 |
| 下から 5 層目 | 「12 桁以下の掛け算」× 4 回 | 172.0782 |
| 下から 6 層目 | 「23 桁以下の掛け算」× 2 回 | 208.0838 |
| 下から 7 層目 | 「46 桁の掛け算」× 1 回 | 254.0838 |
合計で 983.4578 回と見積もることができました。$N = 64$ くらいで、従来の方法とのスピードの差が明らかになってきます。$N$ がさらに大きくなれば、差がもっと明らかになります。
計算時間のオーダーを見積もろう
計算時間のオーダーはどのくらいでしょうか?
簡単のため、$N = 2^{K}$ の場合に、どんな計算をしているのか見てみましょう。
| 下からの段数 | やっている計算 |
|---|---|
| 下から 2 層目 | $K$ 桁くらい2の掛け算が $2^{K-1}$ 回 |
| 下から 3 層目 | $2K$ 桁くらいの掛け算が $2^{K-2}$ 回 |
| 下から 4 層目 | $4K$ 桁くらいの掛け算が $2^{K-3}$ 回 |
| ... | ... |
| 下から $K+1$ 層目 | $2^{K-1} \times K$ 桁くらいの掛け算が $1$ 回 |
したがって、下から $L+1$ 層目については、こんな感じです。
- 下から $L+1$ 層目では、$2^{L-1} \times K$ 桁くらいの掛け算が $2^{K-L}$ 回
- だから、計算時間は $2^{K-L} \times (2^{L-1} \times K) \times \log(2^{L-1} × K)$ つまり $2^{K-1} \times K \times L$ 回程度、と見積もれる!
これを全部足し算して、全体で計算時間は $O(2^{K} \times K^{3})$ になります!
従来の方法だと計算時間は $O(4^{K} \times K^{2})$ になるので、これと比べて圧倒的に速いのが分かります。
$N = \log(K)$ だから、計算時間は $O(2^{\log(N)} \times (\log_2(N))^3) = O(N \times \log^3(N))$ になります。
これを見ると、$100000!$ でも数秒で計算できそうに見えます。元の方法と比べてめっちゃ速いです!
4-1-5. 分割統治法がうまくいった!
どんな感じで計算時間を短くできたか分かりましたか?今回は…
- 小さな 2 つの問題に落とし込んで、この結果をまとめるのが高速にできれば、全体の問題も速く解ける!
というアイデアを使っています。これがまさに「分割統治法」です!
分割統治法で速く解ける問題の例
大きな数の計算とは少し話が違いますが、この問題は「分割統治法」を使って高速に解けます。
「バブルソートの交換回数」という、アルゴリズム分野においては有名な問題です。
長さ $N$ の配列 $A = (A_0, A_1, A_2, \dots, A_{N-1})$ が入力されます。
ここから 2 つの値を取り出す方法は $N \times (N-1) \div 2$ 通りありますが、そのうち「左の値よりも右の値の方が小さくなる」ものがいくつあるのか計算してください。
例えば、$A = (3, 1, 4, 2)$ が入力された場合、$(3, 1), (4, 2), (3, 2)$ を選ぶ $3$ 通りです。
この問題は、左半分の問題と右半分の問題の 2 つに落とし込んで、結果を高速に「まとめる」ことで上手く行きます。例えば、$(3, 1)$ の答えは「1」で、$(4, 2)$ の答えは「1」ですが、転倒数は $1 + 1 + ($いくつか$)$ で「3」と計算できます。上手くやると、この「いくつか」が高速に計算できるから、全通りチェックする計算時間 $O(N^{2})$ の解法よりも高速に解くことができる、というものです。
また、「カラツバ法」や「Toom-Cook 法」にも、「分割統治法」のアイデアが使われています。
もう一度 3 章の内容を振り返って見てみましょう。
4-1-6. かっこいい実装方法
さっきのアルゴリズムは少し複雑になりますが、「キュー (queue)」というデータ構造を使うとわずか 10 行程度で $N!$ の高速な計算プログラムが実装できます!
キュー (queue) とは何か
数が書かれたボールの入った筒みたいなものを想像して、
- ポップ操作:筒の左端から値を取り出す。
- プッシュ操作:筒の右端に値を入れる。
この 2 つの操作が計算時間 $O(1)$ でできます!3 C++ ユーザーにとってはこの説明が分かりやすいと思います。C++ 以外の多くのプログラミング言語は、キューは標準ライブラリとして使うことができます。詳しくは、以下の記事をご覧ください。
結局どうやって実装するのか?
そこで、キューを使うと $N!$ が以下のような感じで計算できます。
- まず、キューを左から順に $(1, 2, 3, ..., N)$ にする。
- キューに 2 つ以上の値が残っている間は、以下の操作を繰り返す。
- キューの左端から 2 個の値を取り出す。これを $b_{1}$ と $b_{2}$ とする。
- ここで、キューの右端に $b_{1} \times b_{2}$ を入れる。この計算は FFT 掛け算を使う。
これで、さっき説明した $O(N \times \log^{3} N)$ で $N!$ を計算する方法と、ほとんど同じようなことが実現できています。計算量はこれと変わらず $O(N \times \log^{3} N)$ になっているので、高速です。
以下、大きな数を扱える「bigint の型」を作ったとして、C++ での実装例を書きます。
シンプルなので、他のプログラミング言語のユーザーでも、簡単に読めると思います。
// ステップ 1:まず que = { 1, 2, 3, ..., N } にする
queue<bigint> que;
for(int i = 1; i <= N; ++i) {
que.push(bigint(i));
}
// ステップ 2:N! を計算する
while(que.size() >= 2) {
bigint b1 = que.front(); que.pop(); // que の先頭の要素を取り出す
bigint b2 = que.front(); que.pop(); // que の先頭の要素を取り出す
que.push(b1 * b2); // que の最後に b1 * b2 を入れる
}
cout << que.front() << endl; // これで N! が出力された!
実際にこのプログラムで、私が作った高速な bigint 型を使って計算すると、
- $100000!$ (456574 桁) がわずか 0.593 秒
- $1000000!$ (5565709 桁) がわずか 9.890 秒
4-1-7. さらに高速なアルゴリズム
実はさらに高速なアルゴリズムがあります。
1983 年、ピーター・ボルウェインさん (カナダの数学者)4 が、$N!$ を $O(N \log^{2}N \times \log(\log N))$ で計算するアルゴリズムを発見し、"On the Complexity of Calculating Factorials" という 5 ページの論文 を書きました。
私は中学 3 年の時にこの論文を読んで、めっちゃ感動して、アルゴリズム理論の世界に引きずり込まれたきっかけでもあります。1983 年という最近の論文なのにめっちゃシンプルですごいです。これを最初に思いついたピーター・ボルウェインさんは天才に違いありません。
これは、$N!$ の素因数分解に基づいています。例えば、
$$10! = 2^{8} \times 3^{4} \times 5^{2} \times 7$$
のようなものを求めます。例えば「$1000!$ は 7 で何回割り切れるか?」という問題は簡単に解くことができます5から、これを $N$ 以下のすべての素数に対して求めます。
ステップ 1
まず、$N$ 以下の素数を全部求めます。「エラトステネスの篩」というアルゴリズムを使うと、この計算に $O(N \times \log(\log N))$ かかります。
ステップ 2
ステップ 1 で求めた $N$ 以下の素数は $N ÷ \log N$ 個程度あります。この全てに対して $N!$ を何回割り切るかを計算します。各素数に対して、計算に最大でも $O(\log N)$ しかかからないので、ステップ 2 は計算時間 $O(N)$ でできます。
これで $N!$ の素因数分解が求まりました。ここまでの計算時間は $O(N \times \log(\log N))$ です。
ステップ 3
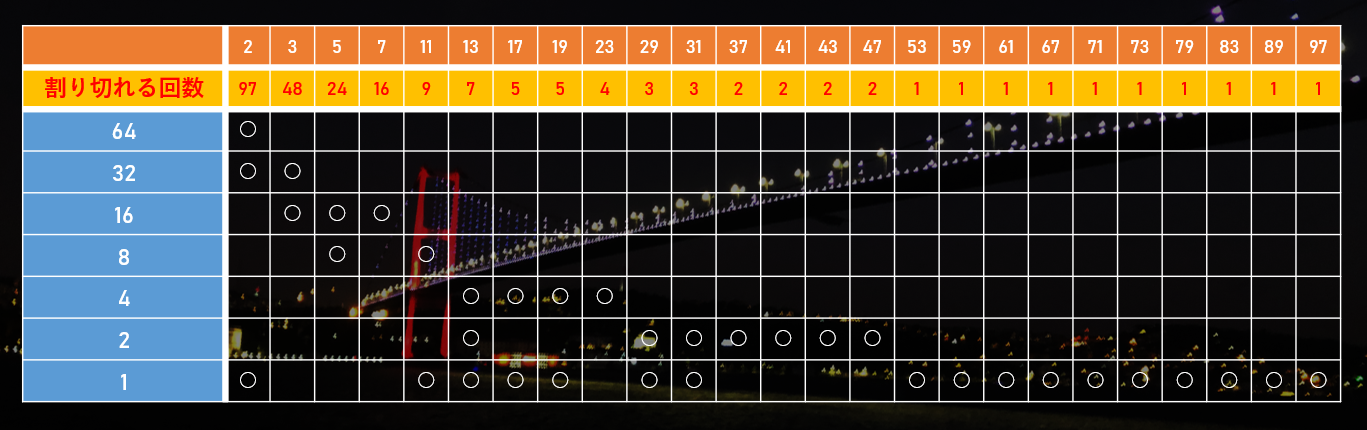
それぞれの素数に対して「何回割り切れるか」の 2 進数を計算します。下図が分かりやすいと思います。これは $100!$ を求める際の計算です。
ステップ 4
丸がつけられた素数の積を、1 の行, 2 の行, 4 の行, 8 の行, … それぞれについて分割統治法を用いて計算します。これを $\alpha_1, \alpha_2, \alpha_4, \alpha_8, \cdots$ とします。例えば上の図の場合で $\alpha_4$ は $13×17×19×23 = 96577$ です。
ステップ 5
$\alpha_1, (\alpha_2)^2, (\alpha_4)^4, (\alpha_8)^8,...$ を「繰り返し 2 乗法」を用いて計算します。これは、例えば $11^{8}$ を計算するのに、
- $11^{2} = 121$
- $121^{2} = 14641$
- $14641^{2} = 214358881$
という感じで 2 乗を繰り返して累乗の値を計算するアルゴリズムです。
ステップ 6
ステップ 5 で求めた $\log N$ 個の値の掛け算を、分割統治法を用いて計算する。
これで $N!$ が求まりました!FFT 掛け算を使うと、計算時間 $O(N \log^{2}N \times \log(\log N))$ になっています。証明は少し難しいのでここでは省略しますが、自信のある読者は自力で考えても良いでしょう。
ちなみに 1994 年に、シューンハーゲさん・グロテフェルトさん・ヴェッターさんによって、$N!$ を計算時間 $O(N \log^{2} N)$ で計算するアルゴリズムが発明され、これが現在最速のアルゴリズムになっています。
4-2. √2 を精度よく求めよう!
$\sqrt{2} = 1.41421356…$ を「一夜一夜にひとみごろ」と暗記した読者さんもいると思います。
こういう人にとっては、$\sqrt{2}$ を計算する方法を知って、びっくりするかもしれません。今から、この値「√2」を計算する方法について書きます。
平方根を求める方法として「開平法」を中学数学とかで習った人もいると思います。確かに、これは $\sqrt{2}$ の小数点以下 $N$ 桁を計算時間 $O(N^{2})$ で求めています。
また、$x^{2} = 2$ となる数 $x$ を二分探索によって求めることもできます。確かに、これは $\sqrt{2}$ の小数点以下 $N$ 桁を計算時間 $O(N^{2} \log N)$ で求めています。
これだと $\sqrt{2}$ の小数点以下 100000 桁が数分で計算できることになります。しかし、もっと速いアルゴリズムがあって、$\sqrt{2}$ の小数点以下 $N$ 桁を計算時間 $O(N \log N)$ で求めています!
掛け算と同じ計算時間オーダーだって、めっちゃ速そうですよね?今からこれを紹介します。
4-2-1. √2 の計算でもニュートン=ラフソン法が登場!
本記事の 3-5 節を読んだ人は、割り算のところでニュートン=ラフソン法が登場したのを覚えていると思いますが、なんとここにもニュートン=ラフソン法が登場します!
ここで、$Y = X^{2} - 2$ のグラフを考えてみましょう。ここで、X 軸 ($Y = 0$ の部分) との交点は $X = \sqrt{2}$ になります6。ここにできるだけ近い位置を計算するのが目標です。
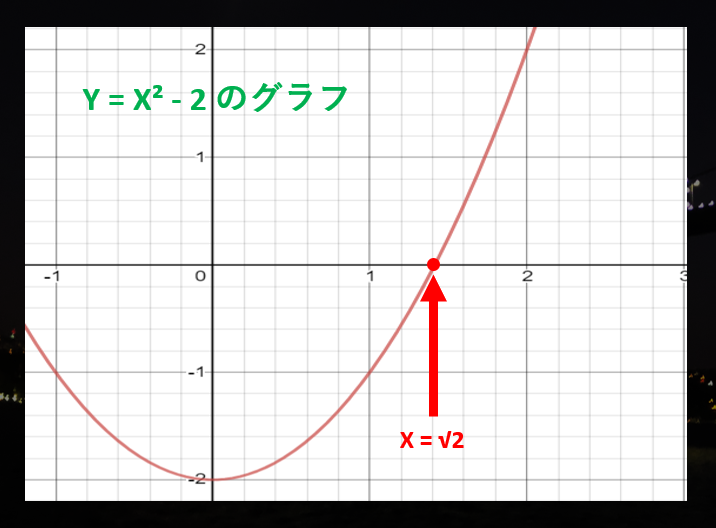
まず、初期値として「$\sqrt{2}$ の値は大体 2 くらいかな?」と設定します。**設定する初期値は、$\sqrt{2}$ 以上にしてください。**ここで、グラフの $X = 2$ の場所に接する直線を引いて、これが X 軸と交わる部分は $\sqrt{2}$ に近づいているはずです。
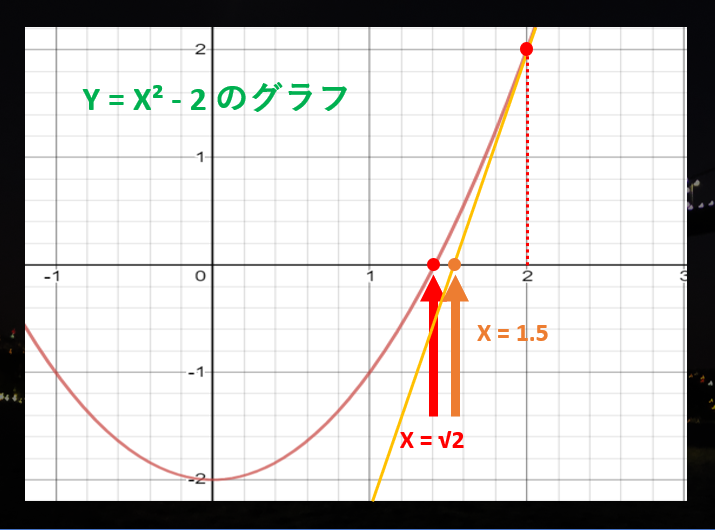
これで答えの新たな予想「$X = 1.5$」が分かりました。この時点で「$\sqrt{2}$ の値は大体 $1.5$ くらいかな?」となっています。ここで、グラフの $X = 1.5$ の場所に接する直線を引いて、これが X 軸と交わる部分は √2 に近づいているはずです。
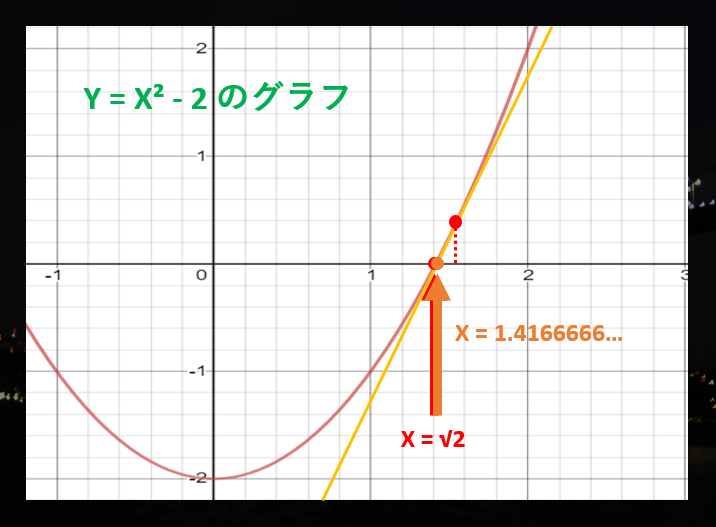
これで答えの新たな予想「$1.4166666...$」が分かりました。この時点で既に 3 桁が一致しています!
このようなステップを繰り返すと、予測値はどんどん近づいていきます。
| ステップ数 | X の値 | 精度 |
|---|---|---|
| 初期値 | 2.0000000000000000000000000 | 0 桁 |
| 1 回終了 | 1.5000000000000000000000000 | 1 桁 |
| 2 回終了 | 1.4166666666666666666666666 | 3 桁 |
| 3 回終了 | 1.4142156862745098039215686 | 6 桁 |
| 4 回終了 | 1.4142135623746899106262955 | 12 桁 |
| 5 回終了 | 1.4142135623730950488016896 | 24 桁 |
$\sqrt{2} = 1.41421356…$ と一致する桁数は、0 桁 → 1 桁 → 3 桁 → 6 桁 → 12 桁 → 24 桁という感じで、どんどん 2 倍ずつ増えています。だから、N 桁を求めるのには大体 $\log N$ ステップしか必要なさそうです。
4-2-2. どうやって「次の予測値」を求めるの?
さっき説明したような方法 (これが「ニュートン=ラフソン法」です!) を使うと、高速に $\sqrt{2}$ が計算できそうです。これは良さそうな方針ですね!
あとは今の予測値から次の予測値を算出する方法が分かれば完璧です。今からこれを説明していきたいと思います。
まず、$Y = X² - 2$ の $X = a$ の場所に接する直線の傾きは「$2a$」で計算できることが知られています7。例えば、グラフの $X = 1.5$ の場所に接する直線の傾きは「$3$」です。
これは、「$X$ が 1 減るにつれ $Y$ が 2a 減る」ということです。ただ、$X = a$ の場所の Y 座標は $a² - 2$ なので、X 軸と交わる場所に "持っていく" ためには、Y 座標を $a² - 2$ 減らす必要があります。
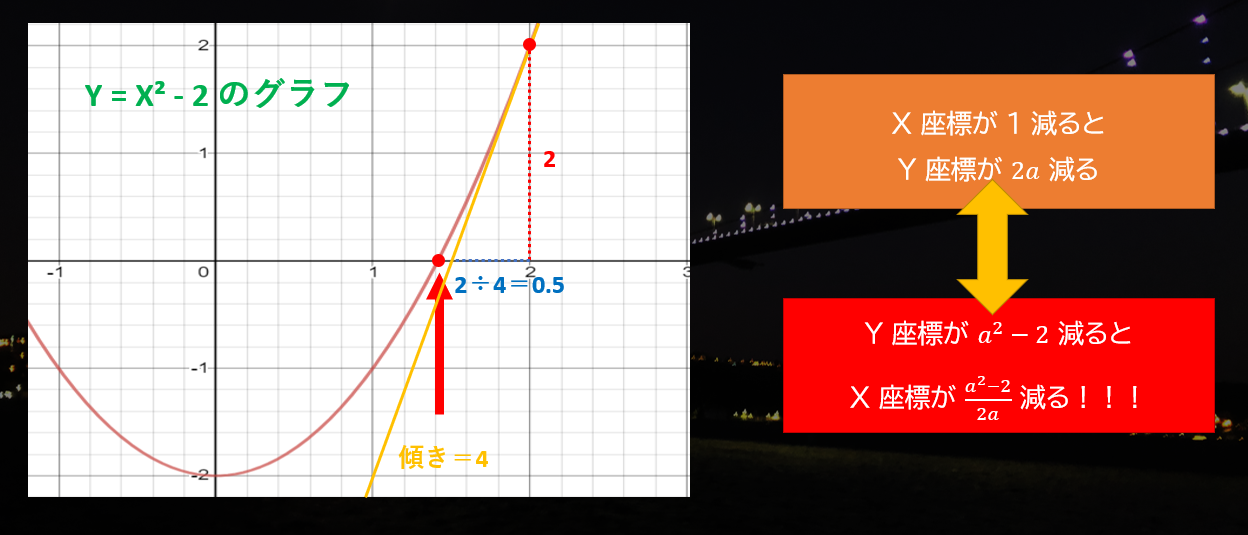
1 ステップで X 座標がどんな感じで減るかが、これで分かりましたね?
この式から、最初の予測値が $X$ のとき、 次の予測値 $X'$ はこう計算できます:
$$X' = X - \frac{X^2 - 2}{2X} = \frac{X^2 + 2}{2X}$$
例えば、$X = 1.5$ が予測値の時は、次の予測値 $X' = (1.5^2 + 2) ÷ (1.5 × 2) = 4.25 ÷ 3 = 1.416666...$ と計算することができます。これは足し算・引き算・掛け算・割り算だけで計算できています!
だから、FFT 掛け算とニュートン=ラフソンの割り算を使えば、1 ステップを $O(N \log N)$ で終わらせることができます。1 ステップで一致する桁数が約 2 倍になることを考えると、$\sqrt{2}$ を小数第 $N$ 桁まで計算するためには大体 $\log N$ ステップ程度必要なので…
**$\sqrt{2}$ の小数点以下 $N$ 桁の計算を $O(N \times \log^{2} N)$ の計算時間でできる**ということです!
これで、人力では到底できないような $\sqrt{2}$ の小数点以下 100 万桁も、わずか 1 分程度で計算できそうです。でも、まだ改善の余地はあります。
4-2-3. 計算量オーダーの改善
(これは 3-5-5 節と同じようなアイデアなので、3 章を読んだ人は思い出してみよう)
例えば、$\sqrt{2}$ の小数点以下 100 万桁をニュートン=ラフソン法で求めるとしましょう。
このとき、最初の数ステップでは、100 万桁の精度で計算する必要はありません。最初の数ステップの時点で、小数点以下 100 万桁まで全部「$\sqrt{2}$ の予測値」を記録しておく必要なんてないんです。この時点で数桁~数十桁の精度しかない状況なのに、100 万桁全部計算しても無駄です。
例えば $X = 17/12$ が現在の予測値の場合、100 万桁全部「$X = 1.4166666666666...$(中略)$...667$」として予測値を記録する必要はなく、「$X = 1.4167$」くらいの記録だけで十分、ということです。
だからステップが進むにつれて、「$\sqrt{2}$ の予測値」の精度の上がり方に応じて、計算する桁数を 2 倍くらいずつ上げていくと良いでしょう。
そうすると、計算回数が
$$1 \times \log(1) + 2 \times \log(2) + 4 \times \log(4) + 8 \times \log(8) + ... + N \times
\log(N)$$
みたいにになって、これを足し算すると、計算時間が $O(N \log N)$ と分かります。
これで、**$\sqrt{2}$ の小数点以下 $N$ 桁の計算を $O(N \log N)$ の計算時間でできる**方法が分かりましたね?
ニュートン=ラフソン法を使うと、$\sqrt{2}$ だけではなく、$\sqrt{3}, \sqrt{4}, \sqrt{5} …$ の場合も初期値さえうまく設定すれば正しく動作します。また、$\sqrt{X}$ の整数部分も $N$ $=$ $(X$ の桁数$)$ として計算時間 $O(N \log N)$ でできます。
4-2-4. 実際に計算してみよう
1 年半前にパ研合宿で講演をした際に作ったプログラムでは、実行時間はこんな感じでした。
(パ研合宿のスライドの 141 ページ目より引用)
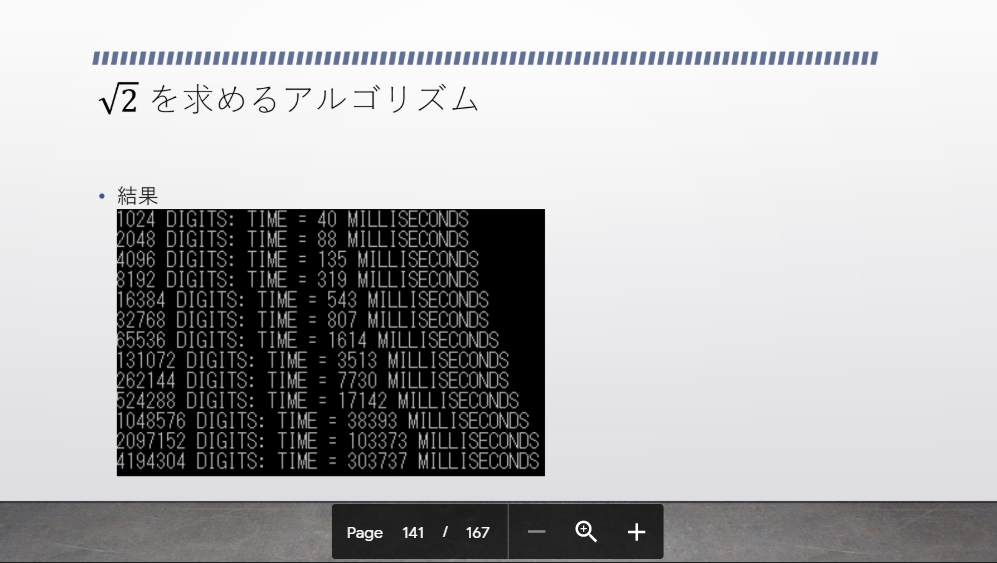
$\sqrt{2}$ の 100 万桁も、かなり短い時間で計算できていることが分かります。
4-2-5. もうひとつのアイデア
実は $\sqrt{2}$ を求める際に、もう一つのアイデアがあります。これは、$(\sqrt{2} - 1)^N$ を求めるやり方です。これは $N$ が大きくなるにつれゼロに近づく性質を使っています。例えば:
$$(\sqrt{2} - 1)^8 = 577 - 408\sqrt{2}$$
これをゼロとみなすと、$408\sqrt{2} = 577$ だから、$\sqrt{2}$ の値を「$577 ÷ 408$」で近似できます。
この値は 1.41421568627... と続き、なんと 6 桁が一致しています!
ここで、$(\sqrt{2} - 1)^2, (\sqrt{2} - 1)^4, (\sqrt{2} - 1)^8, (\sqrt{2} - 1)^{16}, (\sqrt{2} - 1)^{32}, \dots$ と順に、前の値を 2 乗して計算していきます。前の値が $a + b\sqrt{2}$ の形で表されていたら、この 2 乗は $(a^2 + 2b^2) + 2ab\sqrt{2}$ と表されます。だから、掛け算を使うだけで 2 乗が計算できますね?
実際にやってみましょう。
| ステップ数 | 計算 | √2 の予測値 |
|---|---|---|
| #1 | $(\sqrt{2} - 1)^2 = 3 - 2\sqrt{2}$ | 1.5000000000 |
| #2 | $(3 - 2\sqrt{2})^2 = 17 - 12\sqrt{2}$ | 1.4166666666 |
| #3 | $(17 - 12\sqrt{2})^2 = 577 - 408\sqrt{2}$ | 1.4142156862 |
| #4 | $(577 - 408\sqrt{2})^2 = 665857 - 470832\sqrt{2}$ | 1.4142135623 |
わずか 4 ステップで、精度 12 桁になりました。よく見るとニュートン=ラフソン法で初期値を 2 に設定して √2 を求めた際と、各ステップの値が同じになっています。
小数点以下 $N$ 桁を得る上で十分なステップ数は、大体 $\log N$ ステップ程度ですね。各ステップには $a + b\sqrt{2}$ での $a, b$ の桁数を $D$ として計算時間 $O(D \log D)$ かかります。
この $D$ の値が 1 ステップで 2 倍になるので、計算回数が
$$1 \times \log(1) + 2 \times \log(2) + 4 \times \log(4) + 8 \times \log(8) + ... + N \times
\log(N)$$
みたいにになって、これを足し算すると、$O(N \log N)$ になります。最後に $\sqrt{2}$ の値を求めるところで 1 回だけ割り算をしますが、これも計算時間 $O(N \log N)$ です。
だから、この方法でも $\sqrt{2}$ の小数第 $N$ 桁を $O(N \log N)$ で計算できることが分かりました!
2 つの方法を解説しましたが、好きな方でやってよいです。
ただ、$\sqrt{2}$ を求めることに関しては、割り算を 1 回しかしない 4-2-5 節の方法の方が、計算時間の定数倍の意味で若干スピーディーに動くのではと思います。
4-3. 円周率 100 万桁に挑戦!
さて、この記事の集大成がやってまいりました。
円周率をどうやって計算するのかの疑問を持った人は多いと思います。例えば、数学を中心とした展示で有名な科学館「リスーピア」には、円周率の小数点以下 100 万桁までで「44444」が初めて現れるのは何桁目、みたいなものを調べられる展示8がありますが、実際の 100 万桁はどうやって計算してるんだろう?とか。
これには深い歴史があります。
紀元前 250 年頃に、古代ギリシアの数学者アルキメデスは正多角形を使って「3.14」までを計算しました。
この後、西暦 480 年頃に、中国の数学者祖沖之は、正 12,288 角形を使って「3.1415926」までを計算できました。これには円周率 $\pi$ を求めるとても古い方法「劉徽のアルゴリズム」が使われています。
ここからおよそ千年間は、多角形の頂点数を増やしまくりました。正 $10^{40}$ 角形を用いて小数第 38 位まで計算できていました。しかし、まだたったの数十桁です。これは、効率的なアルゴリズムがまだ発見されていない時代でした。
4-3-1. マチンの公式
1671 年、次のような「グレゴリー=ライプニッツ級数」が発見されました。
$$\arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \frac{x^9}{9} - \frac{x^{11}}{11} + \frac{x^{13}}{13} - \cdots$$
ここで、$\arctan(x)$ というのは、次の図の青い部分で表される長さを表しています。
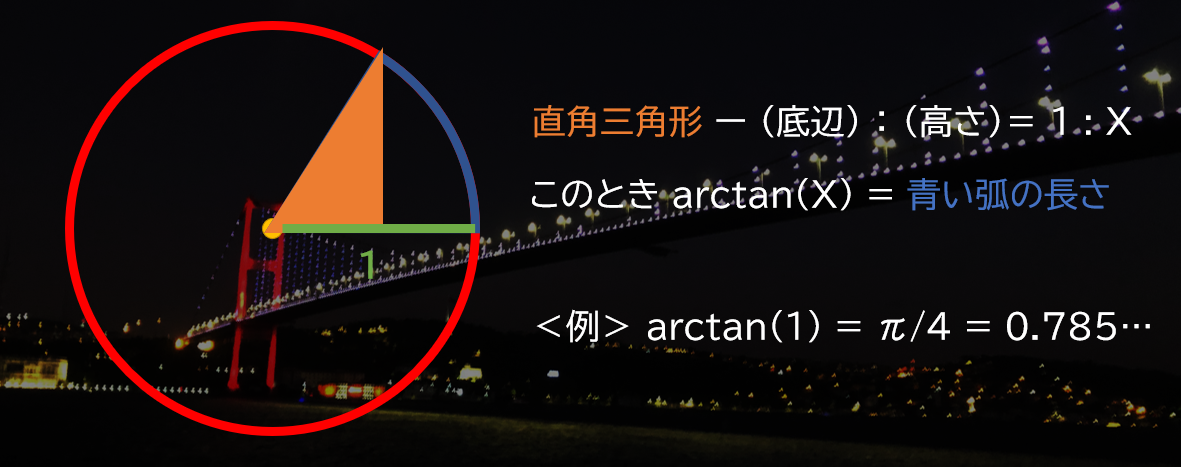
そして、1704 年にイギリスの天文学者ジョン・マチンは、「マチンの公式」を発見しました。
$$\pi = 16 \times \arctan\left(\frac{1}{5} \right) - 4 \times \arctan\left(\frac{1}{239} \right)$$
これは、「(底辺):(高さ) = 5 : 1 の直角三角形 4 つが合わさった角度は、(底辺):(高さ) = 239 : 1 の直角三角形の角度 + 45 度」 ということです!
さて、グレゴリー=ライプニッツ級数と、マチンの公式ができました。この 2 つを組み合わせると…?
$$\arctan\left(\frac{1}{5} \right) = \frac{1}{5} - \frac{1}{3 \times 5^3} + \frac{1}{5 \times 5^5} - \frac{1}{7 \times 5^7} + \frac{1}{9 \times 5^9} - \cdots$$
精度 $N$ 桁で求めるためには、これを $1.5 \times N$ 個くらい計算する必要があります。
$$\arctan\left(\frac{1}{239} \right) = \frac{1}{239} - \frac{1}{3 \times 239^3} + \frac{1}{5 \times 239^5} - \frac{1}{7 \times 239^7} + \frac{1}{9 \times 239^9} - \cdots$$
精度 $N$ 桁で求めるためには、これを $0.4 \times N$ 個くらい計算する必要があります。
さて、ここまでできました。それぞれの割り算は $O(N \log N)$ で計算できるので、円周率 $N$ 桁の計算時間 $O(N^{2} \log N)$ です!しかし、これまでのアルゴリズムよりもシンプルで、十分に速いです。
このマチンの公式を使って、19 世紀の数学者ウィリアム・シャンクス は、15 年もの生涯をかけて円周率 $\pi$ を 527 桁まで計算したことで知られています。
マチンの公式は、少しアルゴリズムを工夫すると9、**掛け算・割り算を筆算でやっても $O(N^{2})$ で計算することができます。**だから第 2 章の内容だけでも、円周率 $\pi$ を 10,000 桁程度なら数分程度の実行時間で計算することができます。
コンピューターが登場した 1949 年、世界最古のコンピューターの 1 つといわれる「ENIAC」を使って、ジョン・フォン・ノイマン10は円周率 2037 桁を計算しました。
その後も、高速な掛け算・割り算のアルゴリズムが開発されるまでの 1960 年代までは、円周率の計算にはマチンの公式をベースにしたアルゴリズムが主に使われていて、1973 年にはフランスのジェン・ギユーとマルティーヌ・ブーイェは円周率 100 万桁の計算に成功したのです!
4-3-2. サラミン=ブレントのアルゴリズム
1975 年、円周率の計算界において画期的な瞬間が訪れます。
ユージン・サラミンとリチャード・ブレントは、以下のような「サラミン=ブレントのアルゴリズム」を開発します。これは以下のようなものです。
$a_0 = 1, b_0 = \frac{1}{\sqrt{2}}$ に設定して、以下の値を $n = 1, 2, 3, \dots$ と順に計算します。
- $a_{n + 1} = \frac{a_n + b_n}{2}$ ($a_n$ と $b_n$ の相加平均)
- $b_{n + 1} = \sqrt{a_n \times b_n}$ ($a_n$ と $b_n$ の相乗平均)
$T = (a_0 - a_1)^2 + 2(a_1 - a_2)^2 + 4(a_2 - a_3)^2 + \cdots + 2^{n-1}(a_{n-1} - a_n)^2$ とします
すると、円周率は $\pi = \frac{(a_n + b_n)^2}{1 - 4T}$ と近似されます!
実際にやってみると、$a_n, b_n$ はこんな感じで変化していき、最終的には一定値に収束します。
| $n$ の値 | $a_n$ の値 | $b_n$ の値 |
|---|---|---|
| 0 | 1.000000000000000 | 0.707106781186548 |
| 1 | 0.853553390593274 | 0.840896415253715 |
| 2 | 0.847224902923494 | 0.847201266746892 |
| 3 | 0.847213084835193 | 0.847213084752765 |
| 4 | 0.847213084793979 | 0.847213084793979 |
| 5 | 0.847213084793979 | 0.847213084793979 |
ループ回数が増えれば増えるほど、精度が増えます。例えば 1 回もループしなかったら円周率 $\pi$ の近似値は
$$1.5 + √2 = 2.914213562...$$
になりますが、回数を増やすにつれ一気に精度が増えます。
| ループ回数 | 円周率の近似値 | 精度 |
|---|---|---|
| 0 | 2.914213562373095048801688724209 | 0 桁 |
| 1 | 3.140579250522168248311331268975 | 3 桁 |
| 2 | 3.141592646213542282149344431982 | 8 桁 |
| 3 | 3.141592653589793238279512774801 | 19 桁 |
| 4 | 3.141592653589793238462643383279 | 41 桁 |
たった 4 回のループで、円周率が 40 桁求まってしまいました!その後も一致桁数は 84 桁 → 171 桁 → 345 桁 → 694 桁 → 1392 桁 → … と、1 回のステップで約 2 倍ずつ増えていきます。
だから、円周率を小数点以下 $N$ 桁求めるのに、$\log N$ ステップ程度しか必要ありません。各ステップでは、$a_{n+1}$ を求めるのに足し算、$b_{n+1}$ を求めるのに掛け算と平方根を求めるので、必要な計算時間は $O(N \log N)$ です。
これで、円周率の小数点以下 $N$ 桁を $O(N \log^{2} N)$ で計算することができます!
4-3-3. 実際に円周率を計算してみた
1 年半前にパ研合宿で講演をした際に、サラミン=ブレントのアルゴリズムを用いて $O(N \log^{2}N)$ で円周率を計算するプログラムを作りました。すると、100 万桁の計算を 613 秒で成功しました!
(パ研合宿のスライドの 156 ページ目より引用)
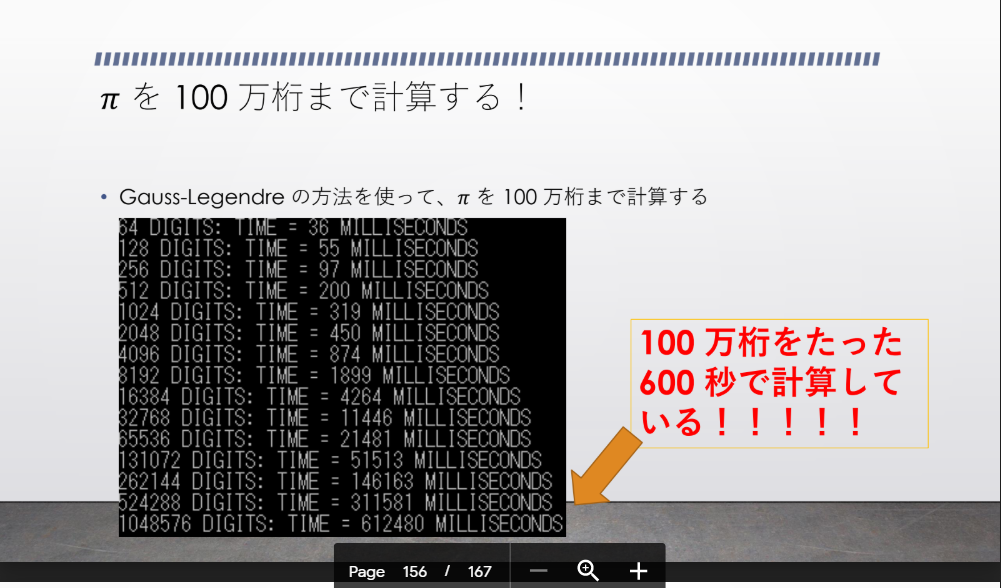
高速な掛け算、高速な割り算、高速な平方根の計算、そしてサラミン=ブレントのアルゴリズムが組み合わさって初めてできました。現代のコンピューターのスピードと、アルゴリズムのパワーの強さが感じられます。
サラミン=ブレントのアルゴリズムが発明されてその後、1982 年に田村良明さんは、サラミン=ブレントのアルゴリズムを用いて 209 万桁の円周率を計算することに成功し、この時点での世界記録を更新しています。
1990 年頃になると、円周率を求める効率的なアルゴリズムが他にも多く開発されました。この頃、東大の金田康正教授 とアメリカのチュドノフスキー兄弟 で何度も円周率計算の世界記録が塗り替えられ、熾烈な競争が行われていました。
2011 年には、長野県の会社員 近藤茂 と、アメリカの大学院生 (当時) アレクサンダー・イー により、円周率 10 兆桁が計算されています。現在の記録は 2020 年 1 月 29 日にティモシー・マリカンが 50 兆桁を計算したものとなっています。
- 円周率10兆桁まで計算 長野の男性 (日本経済新聞) ー これもぜひ読みましょう。
円周率の計算についてもっと詳しく知りたい方は、ぜひこちらも参考にしてください。
- 円周率.jp ー 円周率 $\pi$ の計算について色々な情報が載っているほか、覚え方まで載ってます
4-4. Constants コンテストへのいざない
Sphere Online Judge というプログラミングのサイトには、「Constants」という企画コンテストがあります。これはその名の通り、$\sqrt{2}$ や円周率 $\pi$ といった「定数」を短時間で精度よく求めるコンテストです。
自信のある人はぜひ挑戦してください!でも、25 秒以内の実行時間で最低 150000 桁を計算しなければ 1 点も得られないので非常に難しく、いまだ世界に 22 人しか得点獲得者はいません。
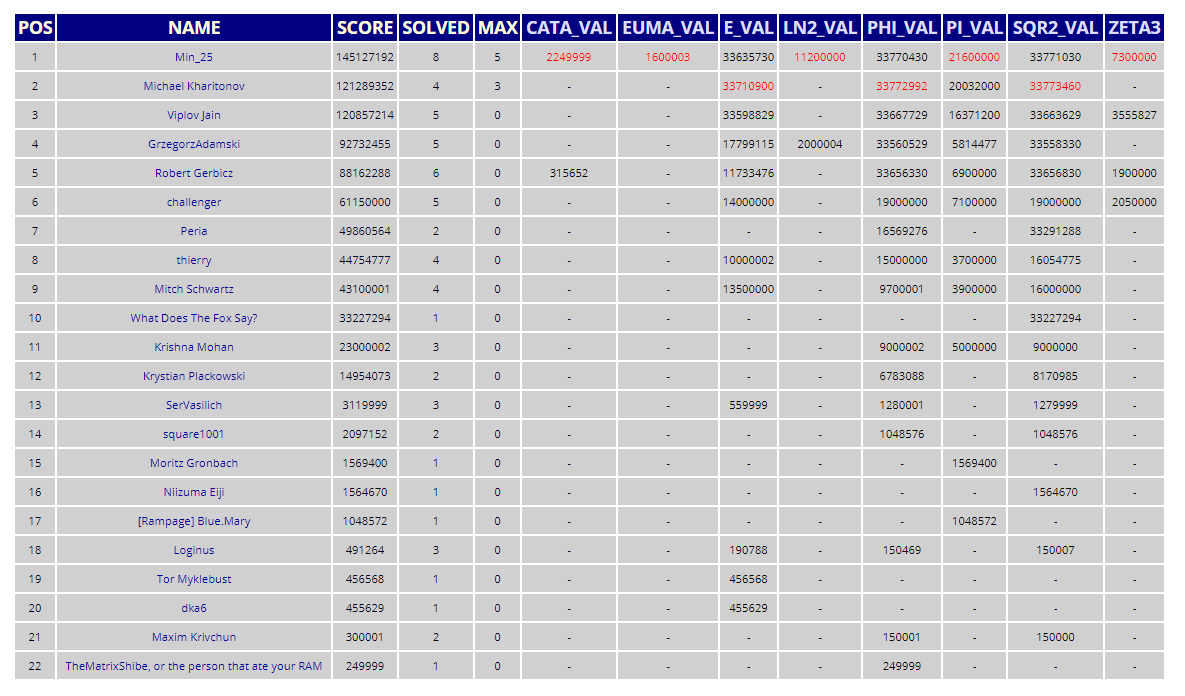
(上のスクリーンショットは、2020 年 6 月 15 日時点での順位表です)
全部で 8 問ありますが、$\sqrt{2} = 1.414213562...$ が一番簡単だと思います。また、Constants でトップの人は、**円周率 $\pi$ をたった 25 秒で 2160 万桁も計算しています。**やばいですよね。
4-5. 大きな数を使った面白い問題の紹介
私がやっている競技プログラミングのサイトの 1 つとして「yukicoder」があります。私はここでよくコンテストに参加しているだけでなく、定期的に問題作成もしていています。
これは私が 2 年ほど前に作った問題です。
最近になってもう一度読み返してみて面白いなと思ったので紹介したいと思います。
長さ $N$ の配列 $(p_0, p_1, p_2, \dots, p_{N-1})$ が入力されます。この配列は $(1, 2, 3, …, N)$ の並び替えになっています。
$(1, 2, 3, …, N)$ の並び替えは $N! = 1 \times 2 \times \cdots \times N$ 通りありますが、これを小さい順に並び替えたときに、$(p_0, p_1, p_2, \dots, p_{N-1})$ は何番目に来るか計算するプログラムを作ってください。
入力される $N$ は $100,000$ 以下で、10 秒以内の実行で答えを求められれば正解となります。
例えば $N = 3$ の場合、$(1, 2, 3)$ の並び替えを小さい順に並べると
$$(1, 2, 3) → (1, 3, 2) → (2, 1, 3) → (2, 3, 1) → (3, 1, 2) → (3, 2, 1)$$
となるので、$(2, 3, 1)$ が入力されたら「4」が答えになります。
もうひとつの例として、$N = 5$ のとき、$(3, 1, 4, 5, 2)$ は「$54$ 番目」となります。
4-5-1. 問題を解く方針
例えば $(5, 2, 3, 6, 4, 1)$ は何番目か、というのを手で解くことを考えます。11
-
ステップ #0:まず一番最初は「5」なので、481 ~ 600 番目
- (1, X, X, X, X, X), (2, X, X, X, X, X), (3, X, X, X, X, X), (4, X, X, X, X, X) の 5! × 4 = 480 個よりも遅い
-
ステップ #1:次は「2」なので、この中で 25 番目 ~ 48 番目 (全体だと 505 ~ 528 番目)
- (5, 1, X, X, X, X) の 4! = 24 個より遅い
-
ステップ #2:次は「3」なので、この中で 7 番目 ~ 12 番目 (全体だと 511 ~ 516 番目)
- (5, 2, 1, X, X, X) の 3! = 6 個より遅い
-
ステップ #3:次は「6」なので、この中で 5 番目 ~ 6 番目 (全体だと 515 ~ 516 番目)
- (5, 2, 3, 1, X, X), (5, 2, 3, 4, X, X) の 2! × 2 = 4 個よりも遅い
-
ステップ #4:次は「4」なので、この中で 2 番目 (全体だと 516 番目)
- (5, 2, 3, 6, 1, X) よりも遅い
こんな感じで解けますね!今回の場合は…?
- ステップ #0 では、現在残っている数で「5」より小さいのは 4 個だから、5! × 4 = 480 が答えに足される
- ステップ #1 では、現在残っている数で「2」より小さいのは 1 個だから、4! × 1 = 24 が答えに足される
- ステップ #2 では、現在残っている数で「3」より小さいのは 1 個だから、3! × 1 = 6 が答えに足される
- ステップ #3 では、現在残っている数で「6」より小さいのは 2 個だから、2! × 2 = 4 が答えに足される
- ステップ #4 では、現在残っている数で「4」より小さいのは 1 個だから、1! × 1 = 1 が答えに足される
最後にそれ自身で 1 が足されるので、$480 + 24 + 6 + 4 + 1 + 1 = 516$ 番目、と計算できます!
つまり、ステップ $i$ の時点で「残っている数のうち $p_i$ よりも小さい数の個数」が求められれば、この順列が何番目なのかが簡単に計算できそうですね。この個数を $b_i$ とすると:
$$b_0 \times (N-1)! + b_1 \times (N-2)! + b_2 \times (N-3)! + \cdots + b_{N-2} \times 1! + 1$$
が答えになります。
$b_0, b_1, b_2, \cdots, b_{N-1}$ の値は、普通にシミュレーションすると全部求めるのに計算時間 O(N²) かかりますが、「Binary Indexed Tree」というデータ構造を使ってうまく計算すると計算時間 $O(N \log N)$ で全部求められます。
Binary Indexed Tree とは?
Binary Indexed Tree は、配列 $v = (v_1, v_2,..., v_N)$ について、次に説明する 2 つの操作を、1 回につき計算時間 $O(\log N)$ で行える、魔法のようなデータ構造です。
- 加算クエリ:$pos$ と $x$ が入力されると、$v_{pos}$ を $x$ 増やす。
- 合計クエリ:$pos$ が入力されると、$v_{1} + v_{2} + ... + v_{pos}$ を計算する。
具体的な実装についてなど、詳しく知りたい方は、このスライドを見るとよいでしょう。
この問題において $b_0, b_1, \cdots, b_{N-1}$ の全てを $O(N \log N)$ で計算するのは意外と簡単です。
長さ N の配列 $v = (v_1, v_2,..., v_N)$ があるとして、$v_i$ は「まだ値 $i$ が残っているならば 1、残っていないならば 0」にします。最初は $v_i$ は全部 1 ですが、ステップを経るにつれ、$v_i = 0$ であるような $i$ の個数が増えていきます。
具体的には、ステップ $i$ では、$pos = p_i$ とすると、残っている数のうち $p_i$ よりも小さい数の個数は、「現時点での $v_1$ から $v_{pos-1}$ までの合計」です。これはまさに Binary Indexed Tree の「合計クエリ」なので、計算時間 $O(\log N)$ で計算できます。
このステップが終われば $p_i$ は残っている数のリストから消えるので、$v_{pos}$ に -1 を加算して 0 にします。これは Binary Indexed Tree の「加算クエリ」なので、計算時間 $O(\log N)$ がかかります。
これで、全体の計算時間 $O(N \log N)$ で $b_0, b_1, \dots, b_{N-1}$ が計算できました!あとは式に当てはめて計算するだけ、と思いたいところですが…
4-5-2. そのままの値なので難しい!
いま、$b_0, b_1, \dots, b_{N-1}$ が高速に計算できました。これが答えになります。
$$b_0 \times (N-1)! + b_1 \times (N-2)! + b_2 \times (N-3)! + \cdots + b_{N-2} \times 1! + 1$$
これは、どのくらいの時間で計算できるでしょうか?残念なことに、$O(N^{2} \log^{2} N)$ かかります。
ステップ $K$ では $b_K$ と $(N-K-1)!$ の掛け算を計算します。しかし、これは大体 $\log N$ 桁と $N \log N$ 桁の掛け算なので、1 ステップにつき $O(N \log^{2} N)$ もかかるのです…
なんか既視感ありませんか?4-1 節「N! を高速な計算」で見たのと似たような状況です。そう、FFT 掛け算のスピードが全く生かせていないのです!
4-5-3. ここで「分割統治法」が登場です!
例えば $N = 16$ の場合を考えます。
左半分と右半分に分けて、次の 2 つの値が求まれば、この 2 つの足し算 (+1) で答えが計算できます。
- 左半分:$b_0 \times 15! + b_1 \times 14! + b_2 \times 13! + \cdots + b_6 \times 9! + b_7 \times 8!$
- 右半分:$b_8 \times 7! + b_9 \times 6! + b_{10} \times 5! + \cdots + b_{14} \times 1! + b_{15} \times 0!$
ここで、左半分 の計算は、
$$b_0 \times (15 \times 14 \times 13 \times \cdots \times 9) + b_1 \times (14 \times 13 \times \cdots \times 9) + \cdots + b_6 \times 8 + b_7$$
を計算する問題に落とし込むことができます。なぜなら、左半分 の値は、これに 8×7×6×5×4×3×2×1 を掛けた値だからです。この掛け算は 2 つの値の桁数が近いので、FFT 掛け算のスピードが生かせそうです!
これで、次の 2 つの値を計算する問題に落とし込めました!
- 左半分:$b_0 \times (15 \times 14 \times 13 \times \cdots \times 9) + b_1 \times (14 \times 13 \times \cdots \times 9) + \cdots + b_6 \times 8 + b_7$
- 右半分:$b_8 \times (7 \times 6 \times 5 \times \cdots \times 1) + b_9 \times (6 \times 5 \times \cdots \times 1) + \cdots + b_{14} \times 1 + b_{15}$
この 左半分 と 右半分 では、元よりも桁数が約半分になっています。つまり、元の半分のサイズの問題 2 つに落とし込むことができた、ということです。
さらなる「落とし込み」
この落とし込んだ 2 つの問題についても、同じようにさらに 2 つに分割できないでしょうか?
ここでは、左半分 の値を、さらに 2 分割することを考えます。このさらなる**左半分と右半分**の値は次のようになっています。
- 左半分:$b_0 \times (15 \times \cdots \times 9) + b_1 \times (14 \times \cdots \times 9) + b_2 \times (13 \times \cdots \times 9) + b_3 \times (12 \times \cdots \times 9)$
- 右半分:$b_4 \times (11 \times 19\times 9) + b_5 \times (10 \times 9) + b_6 \times 9 + b_7$
この**左半分の計算は、
$$b_0 \times (15 \times 14 \times 13) + b_1 \times (14 \times 13) + b_2 \times 13 + b_3$$
を計算する問題に落とし込むことができます。なぜなら、左半分**の値は、これに 12×11×10×9 を掛けた値だからです。この 2 つの掛け算も桁数が近いので、FFT 掛け算のスピードが生かせそうです!
これで、次の 2 つの値を求める問題に落とし込むことができました。
- 左半分:$b_0 \times (15 \times 14 \times 13) + b_1 \times (14 \times 13) + b_2 \times 13 + b_3$
- 右半分:$b_4 \times (11 \times 10 \times 9) + b_5 \times (10 \times 9) + b_6 \times 9 + b_7$
この 左半分 と 右半分 では、元よりも桁数が約半分になっています。つまり、元の半分のサイズの問題 2 つに落とし込むことができた、ということです。
そして、左半分 と 右半分 についても同じように "分割して統治して" 計算する… といった感じです。どんどん小さくしていって、最終的にサイズ 1 の問題から解いていきます。まさに分割統治法のアイデアです。
赤い部分の計算
まだ計算出来ていない値があります。これは、8×7×6×5×4×3×2×1 や 12×11×10×9 などの 赤い部分 の値です!$N = 16$ の場合のサイズ 1 になるまでの 赤い部分 のリストです。
- サイズ 16 のとき:8×7×6×5×4×3×2×1
- サイズ 8 のとき:12×11×10×9 (左半分)、4×3×2×1 (右半分)
- サイズ 4 のとき:14×13 (左半分)、10×9 (右半分)、6×5、2×1
- サイズ 2 のとき:15、13、11、9、7、5、3、1
そのまま求めていたら、時間がかかってしまいます。しかし、下図のような構造を計算すると、なんと全部の計算が、$N!$ を分割統治法で計算する時間と同じ、$O(N \log^{3} N)$ でできてしまうのです!

ここで 赤い部分 の値のリストに載ってる 15 個の数が、STEP #4 までに全て計算されていることが分かると思います。
残りの分割統治法パートも、下から $L$ 番目の層では $2^L \times \log(N)$ 桁オーダーの掛け算をしているので、分割統治法パートの計算時間は $O(N \log^{3} N)$ になります。
**これで、この問題は計算時間 $O(N \log^{3} N)$ で解けました!**速い実装をすると、$N = 100,000$ の入力で 1 秒程度で計算を終わらせることができます。
楽しめましたでしょうか?少し難しかったと思いますが、理解していただけたならばうれしいです。
4-6. 応用編を通して…
これで第 4 章が終わりです!大きな数の計算 (多倍長整数演算) の基本的なことから応用的なことまで述べたので、記事の分量が長くなってしまいましたが、面白かったですか?
ちなみに、英語版の Wikipedia に「Computational Complexity of Mathematical Operations」という素晴らしい記事があります。この記事を書くにあたって、参考資料として使わせていただきました。
ここには、四則演算の計算時間オーダーや、$\sqrt{2}$ や $\pi$ を小数第 $N$ 桁まで計算する計算時間オーダーだけでなく、他にもいろいろ載っています。素晴らしくまとまっている記事なので、人生で一度は読んでおきましょう!
大きな数の計算の実装例
私は大きな数の計算のライブラリを作っていますので、ぜひ見てください。
これは「パ研合宿 2018」で講演するとき、1 年半前に作ったものです。最近もう一度作り始めていて、今作成途中のものがあって、近いアップデートで負の数も扱えるようにしようになる予定です。
5. おわりに
AtCoder をはじめとする競技プログラミングのコンテストでは、答えが大きな数になる数え上げ問題 (例えば 4-5 で出てきたような問題) は、こんな感じの形式で答えを求めることが多いです。
- 「答えは非常に大きくなる場合があるので、これを $1,000,000,007$ で割った余りを求めなさい。」
これは多倍長整数演算を使わずに解けるようにするためです。だから、大きな数の計算を必要とする問題は、競技プログラミングではほとんど出題されないゆえ、あまりよく知られていません。
しかし、この世界をのぞいてみると、こんなにも感動的なアルゴリズムがたくさんあるのはなんと素晴らしい!
私はそう思いながら記事を書きました。なぜなら、私がアルゴリズム理論の世界に面白さを感じた論文 (これは 4-1-7 節で書きました) も、れっきとした「大きな数の計算のアルゴリズム」ですから。
この分野は 2020 年になっても進展し続けています。例えば今までは、「コンピューターの bit 数 (例えば、32 bit のパソコン、64 bit のパソコン) を $B$、コンピューターのメモリサイズを $S$ とするとき、$2^{B}$ が $S$ に応じて動く」という現代のコンピューターモデルを仮定しなかった場合、$O(N \log N)$ で掛け算をするアルゴリズムは発見されていませんでした。
これが 2019 年に解決されたのです!デイヴィッド・ハーヴェイさんとジョリス・ファンデルホーヴェンさんは、N 桁の掛け算を理論的に $O(N \log N)$ で計算できるアルゴリズムを発見しました。
これは 1729 次元のフーリエ変換に基づいたアルゴリズムで、「10 の (10 の 38 乗)」桁以上でなければ動作しないという全く実用的ではないアルゴリズムですが、理論的に大きな壁を突破しています。
- Maths whiz solves 48-year-old multiplication problem by University of New South Wales
発展的な内容だったので、難しく感じたあるいは分からなかったという所もあるかもしれませんが、その場合はコメント欄などで気軽に聞いてください。
最後までこの記事をお読みいただき、ありがとうございました!
謝辞
この記事の文章校正などをしたり、記事を書く上で色々アドバイスをくれた @e869120 さん12に感謝します。
また、この記事は「パ研合宿 2018」での私の講演から生まれた記事であります。2018 年のクリスマスイブに私の 150 分の講演を聞いてくれた、この時点で中 1 から高 2 までにわたる参加者二十数名に感謝します。本当にありがとうございます。
そして、記事のタイトル決めの相談に乗ってくれた @drken さんもありがとうございます!
-
実際の FFT 掛け算は計算時間の定数倍が 10 ~ 数十程度あります。ただこれも FFT の実装 (再帰で実装するか・非再帰で実装するかなど) によって変わります。また、1 桁ごとではなく 5 桁ごととかで数を管理すると、また速くなったりします。 ↩
-
ここでは K 桁くらいと書いていますが、「K 桁オーダー」というのは、大体 K × (定数) 桁くらい、ということです。今回の場合は、K がいくら大きくても 0.3 × K 桁程度になるので「K 桁オーダー」です。今回の場合、下から L+1 層目では、0.3 × K 桁くらい (= N くらい) の数の掛け算を 2K-L 回やります。 ↩
-
これは数値型の場合です。例えば 10 万桁の大きな数をキューに入れる場合、10 万回の計算が必要です。 ↩
-
「円周率を 16 進数で求めた時に、前の桁を求めずに特定の桁を計算できる」特殊な公式として有名な Bailey-Borwein-Plouffe の公式を作った人でもあります。 ↩
-
1000! が 7 で割り切れる回数は、1000/7 = 142、142/7 = 20、20/7 = 2、2/7 = 0 になるから、142 + 20 + 2 = 164 回割り切れる、という感じで簡単に計算できます。中学受験や高校受験を経験した人は、これを思い出してみると良いでしょう。 ↩
-
実際は X = -√2 も X 軸上にありますが、ここでは考えないことにします。 ↩
-
高校 2 年の数学で習う「微分」を知っておくと理由が分かります。「Y = X² - 2」を微分すると、「Y' = 2X」になります。これは、グラフ上の X = a の場所に接する直線の傾きが 2a である、ということです。微分を知らなくても、0, 1, 4, 9, 16, 25, 36, 49,… と続く数の並びの K 番目と K+1 番目の差が大体 2K になることで、なんとなく分かると思います。 ↩
-
私もプレイしたことがあります。5 桁まで入力できますが、その中で「100 万桁の中に登場しない数」は両手の指で数えられるほどしかありません。 ↩
-
例えば arctan(1/239) を計算する際に、100000...(中略)...00000 をどんどん 239 で割っていきます。これは、4184100418..., 1750669631..., 7324977536..., という感じでどんどん減っていくと思いますが、1 ステップの 239 で割る計算は桁数を N として計算時間 O(N) でできます。最終的に、求めた値を 1, 3, 5, 7, 9, 11, 13, ... で割って、これを足し算します。そうすると、筆算だけで N 桁の arctan を O(N²) で計算することができ、O(N²) で円周率を計算することができます。 ↩
-
20 世紀最大の天才の 1 人。コンピューターの開発だけでなく、原子爆弾の開発にもたずさわった。 ↩
-
問題をプログラミングで解くときも、紙と鉛筆で解いたらどうやって解くのかをイメージすると、問題を解く方針やアルゴリズムが考えやすくなります。 ↩
-
@e869120 氏は私の双子のもう片方で、競技プログラミングに強いです。AtCoder では 2020 年 6 月 12 日時点では「レッドコーダー」であるほか、Qiita にも「レッドコーダーが教える、競プロ・AtCoder上達のガイドライン」など数々の人気記事を投稿しています。 ↩