「ゼロから作るDeep Learning」(斎藤 康毅 著 オライリー・ジャパン刊)を読んでいる時に、参照したサイト等をメモしていきます。 その10 ← →その12
7章 畳み込みニューラルネットワーク になると、6章までやってきたのとかなり違うように見えます。これまでと違うことをいろいろやっているように見えますが、最後には重みとバイアスの勾配を求めて格納することになります。
つまり、基本原理はまったく変わらず、変わったのは入力データで
P207
入力データが画像の場合、画像は通常、縦・横・チャンネル方向の3 次元の形状です。しかし、全結合層に入力するときには、3 次元のデータを平ら―― 1 次元のデータ――にする必要があります。実際、これまでのMNIST データセットを使った例では、入力画像は(1, 28, 28)―― 1 チャンネル、縦28 ピクセル、横28 ピクセル――の形状でしたが、それを1 列に並べた784 個のデータを最初のAffine レイヤへ入力しました。
・・・
一方、畳み込み層(Convolution レイヤ)は、形状を維持します。画像の場合、入力データを3 次元のデータとして受け取り、同じく3 次元のデータとして、次の層にデータを出力します。そのため、CNN では、画像などの形状を有したデータを正しく理解できる(可能性がある)のです。
実際、私自身もこの自習メモその6の2で、Kaggleの猫と犬のデータセットを処理するときには、3次元のデータを1次元に変換して使っています。これを3次元で処理できれば、認識率も向上するかもしれません。
畳み込み層、パディング、ストライド
これらの説明は、決して難しいわけではなく、それなりにわかるのですが、P212に、突然こんな式が出てくるので、これは何だ? ホントにそうか? ということで、考えてみました。
$OH = \frac{H + 2P - FH}{S} + 1$
$OW = \frac{W + 2P - FW}{S} + 1$
とりあえず、S(ストライド)は無い事にして考えて見ます。
入力サイズとフィルタのサイズについて、いくつか確認してみると
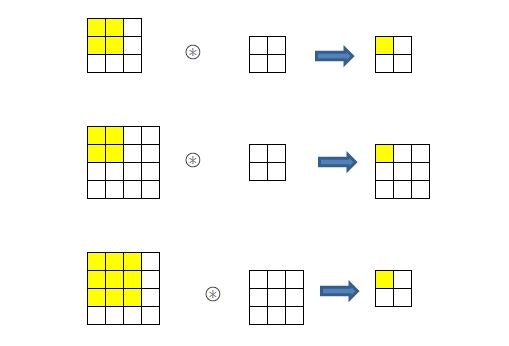
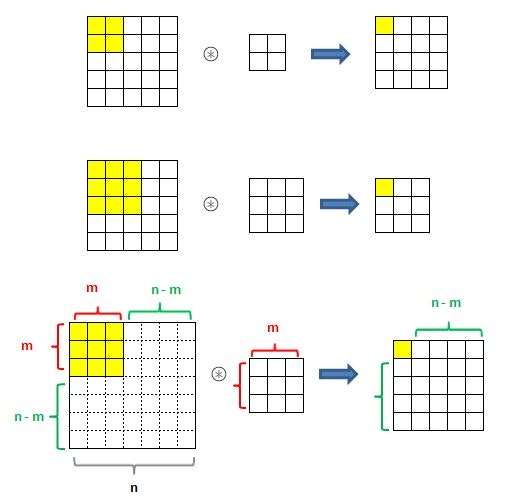
入力サイズ(n、n)とフィルタサイズ(m、m)のとき、
出力サイズは(n-m+1、n-m+1)となるようです。
左上隅にフィルタをあてると、右側にあと(n-m)回動ける。下に(n-m)回動けます。
だから、左上隅の分1を足して、n-m+1 ということでしょうか。
では、ストライドsがあるとどうなるか?
ストライドが2のとき、右側に(n-m)回動けたのが、半分になります。(n-m)/2
3のときは3分の1になります。
つまり、動ける回数が(n-m)/s になるので、
出力サイズは(n-m)/s+1 ということになります。
入力データのサイズが(H、W)、パディングがP、フィルタサイズが(FH、FW)とすると
n=H+2×P 同じく n=W+2×P
m=FH n=FW
なので、
出力サイズは
OH=(H+2×P-FH)/s + 1
OW=(W+2×P-FW)/s + 1
この式から、ストライドが1で、フィルタサイズが3,5,7という奇数の時に、パディングを1,2,3と指定すると、入力サイズと同じ大きさの出力サイズになることがわかります。
MNISTデータの学習とテスト
P230から、MNISTデータを学習させるための例として、クラスSimpleConvNetの説明があります。
このクラスを使って学習させ
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from dataset.mnist import load_mnist
from common.simple_convnet import SimpleConvNet
from common.trainer import Trainer
# データの読み込み
(x_train, t_train), (x_test, t_test) = load_mnist(flatten=False)
max_epochs = 20
network = SimpleConvNet(input_dim=(1,28,28),
conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
trainer = Trainer(network, x_train, t_train, x_test, t_test,
epochs=max_epochs, mini_batch_size=100,
optimizer='Adam', optimizer_param={'lr': 0.001},
evaluate_sample_num_per_epoch=1000, verbose=False)
trainer.train()
テストデータの判定内容を検証してみました。
import numpy as np
from common.simple_convnet import SimpleConvNet
from dataset.mnist import load_mnist
import pickle
import matplotlib.pyplot as plt
def showImg(x):
example = x.reshape((28, 28))
plt.figure()
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(example, cmap=plt.cm.binary)
plt.show()
return
# テストデータで評価
x = x_test
t = t_test
network = SimpleConvNet(input_dim=(1,28,28),
conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
hidden_size=100, output_size=10, weight_init_std=0.01)
network.load_params("params.pkl")
y = network.predict(x)
accuracy_cnt = 0
for i in range(len(x)):
p= np.argmax(y[i])
#print(str(x[i]) + " : " + str(p))
if p == t[i]:
accuracy_cnt += 1
else:
print("正解:"+str(t[i])+" 推論結果:"+str(p))
showImg(x[i])
print("Accuracy:" + str(float(accuracy_cnt) / len(x)))
結果、正解率は
Accuracy:0.988
しかし、6万件のデータ処理に何時間もかかりました。
さらに、学習した後、テストデータの処理をしようとしても、メモリ不足の問題に足をとられて、なかなか先に進めませんでした。メモリ4GぽっちではDeep Learningはムリなのでしょうか?
とりあえず、CNNで精度が高い学習ができたことは確認できました。
で
例によって、プログラムの内容を追って見たいと思います。
SimpleConvNetクラス
# coding: utf-8
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import pickle
import numpy as np
from collections import OrderedDict
from common.layers import *
from common.gradient import numerical_gradient
class SimpleConvNet:
def __init__(self, input_dim=(1, 28, 28),
conv_param={'filter_num':30, 'filter_size':5, 'pad':0, 'stride':1},
hidden_size=100, output_size=10, weight_init_std=0.01):
filter_num = conv_param['filter_num']
filter_size = conv_param['filter_size']
filter_pad = conv_param['pad']
filter_stride = conv_param['stride']
input_size = input_dim[1]
conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
# 重みの初期化
self.params = {}
self.params['W1'] = weight_init_std * \
np.random.randn(filter_num, input_dim[0], filter_size, filter_size)
self.params['b1'] = np.zeros(filter_num)
self.params['W2'] = weight_init_std * \
np.random.randn(pool_output_size, hidden_size)
self.params['b2'] = np.zeros(hidden_size)
self.params['W3'] = weight_init_std * \
np.random.randn(hidden_size, output_size)
self.params['b3'] = np.zeros(output_size)
# レイヤの生成
self.layers = OrderedDict()
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
self.layers['Relu1'] = Relu()
self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
self.layers['Affine1'] = Affine(self.params['W2'], self.params['b2'])
self.layers['Relu2'] = Relu()
self.layers['Affine2'] = Affine(self.params['W3'], self.params['b3'])
self.last_layer = SoftmaxWithLoss()
def predict(self, x):
for layer in self.layers.values():
x = layer.forward(x)
return x
def loss(self, x, t):
y = self.predict(x)
return self.last_layer.forward(y, t)
def accuracy(self, x, t, batch_size=100):
if t.ndim != 1 : t = np.argmax(t, axis=1)
acc = 0.0
for i in range(int(x.shape[0] / batch_size)):
tx = x[i*batch_size:(i+1)*batch_size]
tt = t[i*batch_size:(i+1)*batch_size]
y = self.predict(tx)
y = np.argmax(y, axis=1)
acc += np.sum(y == tt)
return acc / x.shape[0]
def gradient(self, x, t):
# forward
self.loss(x, t)
# backward
dout = 1
dout = self.last_layer.backward(dout)
layers = list(self.layers.values())
layers.reverse()
for layer in layers:
dout = layer.backward(dout)
# 設定
grads = {}
grads['W1'], grads['b1'] = self.layers['Conv1'].dW, self.layers['Conv1'].db
grads['W2'], grads['b2'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
grads['W3'], grads['b3'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
return grads
def save_params(self, file_name="params.pkl"):
params = {}
for key, val in self.params.items():
params[key] = val
with open(file_name, 'wb') as f:
pickle.dump(params, f)
def load_params(self, file_name="params.pkl"):
with open(file_name, 'rb') as f:
params = pickle.load(f)
for key, val in params.items():
self.params[key] = val
for i, key in enumerate(['Conv1', 'Affine1', 'Affine2']):
self.layers[key].W = self.params['W' + str(i+1)]
self.layers[key].b = self.params['b' + str(i+1)]
レイヤを積み上げているところが違ってるだけで、他はMultiLayerNetクラスとたいして変わりません。
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
Convolutionクラスもlayers.pyの中で定義されていて
class Convolution:
def __init__(self, W, b, stride=1, pad=0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
# 中間データ(backward時に使用)
self.x = None
self.col = None
self.col_W = None
# 重み・バイアスパラメータの勾配
self.dW = None
self.db = None
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = 1 + int((H + 2*self.pad - FH) / self.stride)
out_w = 1 + int((W + 2*self.pad - FW) / self.stride)
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
self.x = x
self.col = col
self.col_W = col_W
return out
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0,2,3,1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
im2col
その肝になるのが im2col 関数。util.pyで定義されていて
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
で、こいつがメモリ不足を引き起こす元凶のようです。
処理するデータ行数が増えると、ここでMemorryErrorになります。
最初の3行では、入力データのサイズを確認し、入力サイズとフィルタサイズから出力サイズを計算しています。ストライドでの割り算で // を使っているのは、割り切れなかった場合には小数点以下を切り捨てるためのようです。
今回の入力データMNISTのテストデータのサイズの確認
x_test.shape
(10000, 1, 28, 28)
データ件数10000 チャネル 1 高さ 28 横幅 28
フィルタW1のサイズ確認
network.params['W1'].shape
(30, 1, 5, 5)
フィルタ数30 チャネル 1 高さ 5 横幅 5
パディング、ストライド
conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1},
networkオブジェクト生成時に、パディング0、ストライド1を指定している。
畳み込み層(Convolution レイヤ)の出力サイズ
$OH = \frac{H + 2P - FH}{S} + 1$ = (28 + 0 - 5)/1 +1 = 24
$OW = \frac{W + 2P - FW}{S} + 1$ = (28 + 0 - 5)/1 +1 = 24
となるはず。
network.layers['Conv1'].forward(x_test).shape
(10000, 30, 24, 24)
データ件数10000 フィルタ数30 出力の高さ 24 出力の横幅 24
Convolution レイヤの追跡
self.layers['Conv1'] = Convolution(self.params['W1'], self.params['b1'],
conv_param['stride'], conv_param['pad'])
class Convolution:
(略)
def forward(self, x):
FN, C, FH, FW = self.W.shape # 30, 1, 5, 5
N, C, H, W = x.shape # 10000, 1, 28, 28
out_h = 1 + int((H + 2*self.pad - FH) / self.stride) # 24
out_w = 1 + int((W + 2*self.pad - FW) / self.stride) # 24
col = im2col(x, FH, FW, self.stride, self.pad)
(略)
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
N, C, H, W = input_data.shape # 10000, 1, 28, 28
out_h = (H + 2*pad - filter_h)//stride + 1 # 24
out_w = (W + 2*pad - filter_w)//stride + 1 # 24
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
input_data は4次元で(データ行数10000、チャネル1、高さ28、横幅28)
pad=0 のときは、[(0,0), (0,0), (0, 0), (0, 0)]パディングしない。
pad=1 のときは、[(0,0), (0,0), (1, 1), (1, 1)]高さと横幅の上下左右に1つずつパディングする。
今回のプログラム例では、pad=0です。input_dataと同じものがimgにセットされます。
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w)) #10000, 1, 5, 5, 24, 24
入力データ(画像イメージ)を、配列colに展開するのだが、データを展開する入れ物として、配列colを作り、いろいろやってから、転置とか列の入れ替えとかreshapeやっています。
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
ここのイメージがまったくつかめないので、次のような簡略化した配列でテストしてみた。
import numpy as np
N=1
C=1
H=8
W=8
filter_h=4
filter_w=4
stride=2
out_h=3
out_w=3
img= np.arange(64).reshape(N, C, 8, 8)
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
col
array([[ 0., 1., 2., 3., 8., 9., 10., 11., 16., 17., 18., 19., 24., 25., 26., 27.],
[ 2., 3., 4., 5., 10., 11., 12., 13., 18., 19., 20., 21., 26., 27., 28., 29.],
[ 4., 5., 6., 7., 12., 13., 14., 15., 20., 21., 22., 23., 28., 29., 30., 31.],
[16., 17., 18., 19., 24., 25., 26., 27., 32., 33., 34., 35., 40., 41., 42., 43.],
[18., 19., 20., 21., 26., 27., 28., 29., 34., 35., 36., 37., 42., 43., 44., 45.],
[20., 21., 22., 23., 28., 29., 30., 31., 36., 37., 38., 39., 44., 45., 46., 47.],
[32., 33., 34., 35., 40., 41., 42., 43., 48., 49., 50., 51., 56., 57., 58., 59.],
[34., 35., 36., 37., 42., 43., 44., 45., 50., 51., 52., 53., 58., 59., 60., 61.],
[36., 37., 38., 39., 44., 45., 46., 47., 52., 53., 54., 55., 60., 61., 62., 63.]])
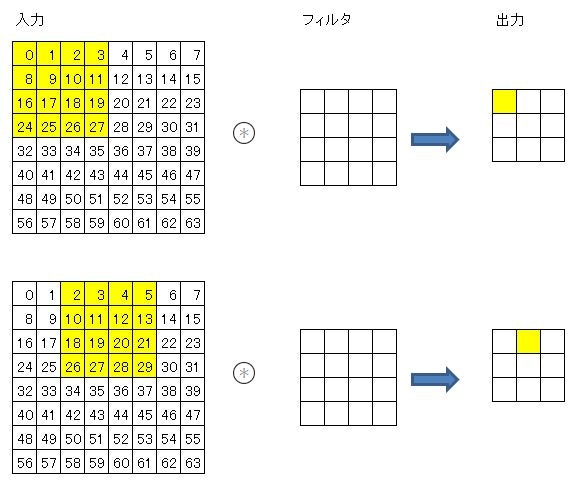
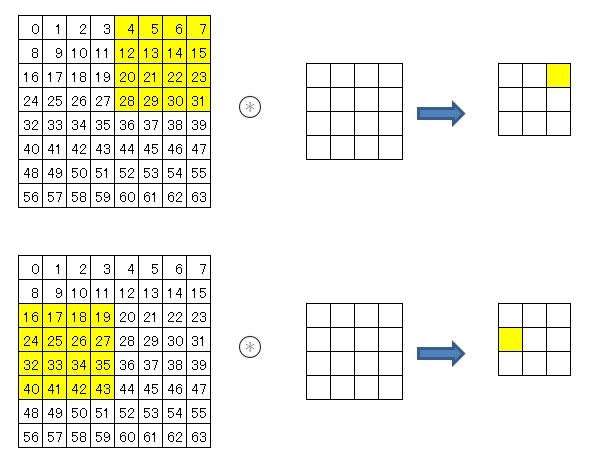
col[0]は、入力データの中の最初にフィルタを適用させる部分が抜き出されている。
col[1]は、ストライド2で右に2つずらしてフィルタを適用させる部分である。
以下、9回フィルタを適用させる部分を抜き出して並べた配列になっている。
途中経過は、はっきり言って何をやっているのかよくわからないのですが、出てきた結果はなんとなくわかります。
4×4のフィルタを1列にreshapeして、colとdot演算すれば、9回フィルタを適用した結果を1回の演算で求める事ができます。
# Convolution.forward
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
このようになると本には書いてあるんですが、やっぱり実際にプログラムを実行して、中のデータを見てみないと理解できませんね。
集計の過程を図にしてみると、画像の最小単位の画素を1つずつ別々に処理するのではなく、その周辺の画素も含めて処理をしていることがわかります。ということは、その範囲に連続した線が引かれていたら、それが縦に引かれているのか、横なのか、斜めなのかが集計結果に出てくるということ。畳み込みでデータを圧縮しているだけでなく、画像の特徴も抽出しているということが、なんとなく理解できるようになりました。
参考
numpy.pad関数完全理解
二次元配列を自在に操れ。【初期化・参照・抽出・計算・転置】
画像処理でよく使われる畳み込みニューラルネットワークとは