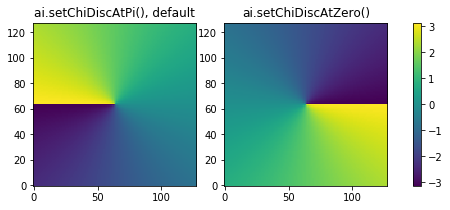pyFAIを使って二次元強度分布を一次元化する

はじめに

二次元検出器のデータをマッピングしたカラフルな図はスライドや原稿の見栄えをよくしたりデータ全体の定性的な変化を追うのに適している一方、定量的な変化を追うには何らかの方法で二次元データを一次元化することが多いです。二次元データ上のある点（通常はビーム中心）を基準にした円環やある方向の扇形あるいは三角形の領域に含まれるピクセルの強度を足して一次元データを作ることをazimuthal integrationと呼びます。基本的なアイディアは、二次元データを入れたNumpy arrayの各要素に対応する極座標を計算して¹円環や扇に含まれるピクセルの強度を積分するだけなのですが、一部が積分領域からはみでてしまう境界付近のピクセルの扱い(pixel splitting)が少々面倒です。EUの放射光実験施設ESRFの専業プログラマーが中心になって開発されたPythonパッケージ pyFAI にはCythonで実装された高速なpixel splitting機能がついている上に、GPUを使ったさらなる高速処理も可能です²。この記事では、__pyFAIを使って円環と扇形（今回は三角形）領域内の強度を一次元データにする方法と、ついでに二次元データの軸をピクセルベースから極座標に変換して展開図³を作成する方法__を述べます。pyFAIの初級チュートリアル とほぼ同じような内容ですが、自分でも確認しておきたかったちょっとした検証を加えています。執筆時2018年1月の段階では日本語情報が皆無ですし公式ドキュメントもあまり充実しているとは言えないので、人数は少ないでしょうが「pyFAI 使い方」で検索している人には役に立つ内容だと思います。

こんなデータが対象

X線回折、SAXSやSANSの小角散乱といった__二次元検出器を使ったX線、中性子散乱実験全般のデータが対象__です。私は使ったことがありませんが、放射光実験で必須であろう検出器ジオメトリーの各種補正もできるようです。この記事では小角散乱での利用を想定しています。

pyFAIでできること

General introduction to PyFAI からかいつまんで箇条書きにしました。

• 二次元強度データの一次元化 (integrate1d, integrate_radial)
• 極座標ベースのマッピングへの変換（integrate2d）
• Cythonによる高速なpixel splitting
• データの前処理（maskingと平均）
• 検出器のジオメトリー関連のキャリブレーション（FIT2Dからの読み込み可）
• 標準試料の回折データからのキャリブレーションも可能
• FabIOライブラリを使っているので12メーカーの20個のデータ形式を直接読み込み可能
• poniファイルを読み込み可能
• GPUを使った並列演算（PyOpenCLを利用）

この記事では最初の二つのみ利用します。私は使ったことがありませんが、主要な機能についてはPythonの知識がなくとも使えるGUIとCUIの pyFAI script が用意されています。今回の内容は Integration tool でも実行可能なはずです。

前提知識

小角散乱のジオメトリー

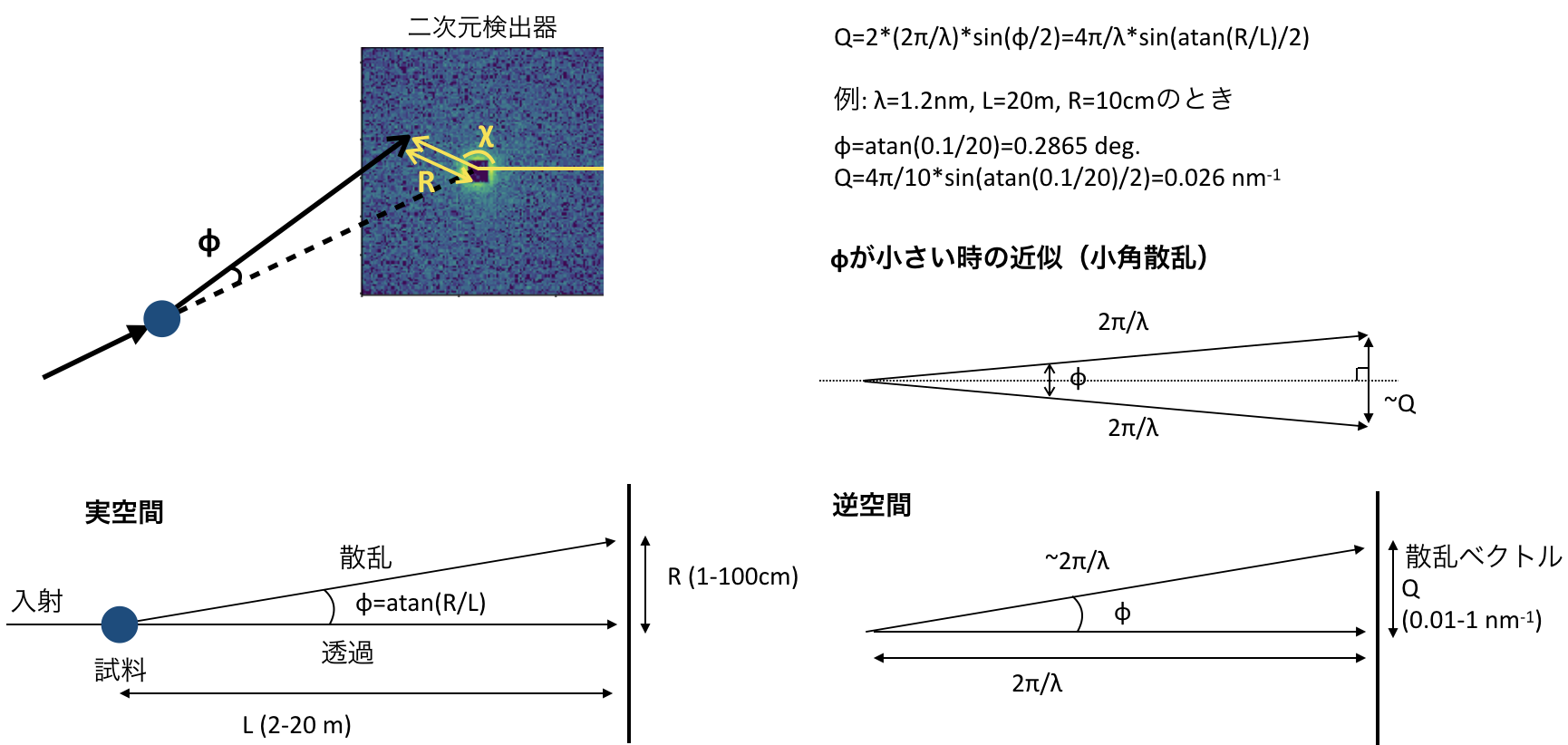
小角散乱に慣れてない人のために今回の記事で最低限必要な小角散乱に出てくる幾何をまとめました。途中の計算でいくつかの距離や角度が出てきますが、最終的に重要なのは散乱ベクトル$Q$とアジマス角$\chi$です。

Numpy arrayとmatplotlib

データは全てNumpy arrayとして扱いますが、大したことはしないのでslicing (data[:10, :]) やboolean indexing (data[data>10]) 程度の知識があれ大丈夫です。ただし、正方形の二次元データ特有の注意点があるので N行N列のnumpy arrayを扱う際に気をつけるべき方向と座標の定義 をあらかじめ読んでおくと混乱を防げると思います。ポイントはNumpy arrayの行と列とグラフ作成時の横軸xと縦軸yを混同しないことです。

また、通常2次元numpy arrayのピクセル座標はピクセルの中央を基準にして考えますが、pyFAIのピクセル座標はピクセルの左下が基準になっています。したがってpyFAIにビームセンターの位置を設定する際はピクセル中央を基準としたxとy座標に0.5ずつ足す必要があります。
詳細はN行N列のnumpy arrayを扱う際に気をつけるべき方向と座標の定義 > pyFAIで一次元化する際も座標の定義に注意を参照してください。

説明用の図を作るのに少しだけ凝ったmatplotlibの使い方をしています。本筋ではないのでmatplotlib関連のコードは無視しても良いのですが、この記事のタイトルにピンときた人にとってはこの先役立つテクニックやレシピが一つくらいは含まれていると思うので是非追ってみてください。データはすべて計算で作ったものなので、matplotlib 2.1.1で該当コードを実行すれば同じグラフが出来上がるはずです。patchやLocatorやFormatterと聞いてもなんのことかわからない人は、matplotlibの部分のコードを解読する前に 早く知っておきたかったmatplotlibの基礎知識、あるいは見た目の調整が捗るArtistの話 を読んでおくことをおすすめします。

手順の全体像

pyFAI.AzimuthalIntegratorクラスオブジェクトのintegrate1dとintegrate_radialメソッドを使うと二次元データの一次元化（横軸はそれぞれ散乱ベクトル$Q$とアジマス角$\chi$）が、integrate2dメソッドを使うとピクセル座標から極座標へのマッピングができます。何に対して何を使ってどんなグラフができるかを簡単な図にまとめました。

一般的な作業手順は以下の通りです。

1. ビームセンター計算（今回は省略）
2. pyFAI.AzimuthalIntegraterオブジェクト(ai)にビームセンターや波長などのパラメータを設定
3. aiのメソッドであるintegrate1d, integrate_radial, integrate2dを実行
4. グラフ作成と調整（今回はmatplotlibを使用）

この記事の目的はpyFAIの基本的な使い方を説明することですが、正直言って2と3は大した作業ではありません。問題は4です。matplotlibで作ったグラフの調整は付け焼き刃の使い方しか知らないと往往にして苦労することが多いからです⁴。ここに時間をかけたくない場合は、pyFAIで作成したデータをファイルに出力して、グラフ作成には使い慣れた他のソフトを使うのもありだと思います⁵。

準備

# どちらかの方法でインストール
pip install pyFAI
conda install pyfai -c conda-forge

どちらも他に必要なパッケージも自動的にインストールしてくれるはずですが、私の場合はopenclだけ抜けており初めてimportしたときにエラーがでました。pyFAIのimport時に何かが足りないと怒られたら適宜インストールしてください。また、pyFAIはまだver 1.0に到達しておらず、だいたい数ヶ月おきに新しいバージョンがリリースされているので、たまにアップデートすることをおすすめします。もし、将来の修正によってここに書いてあるコードでエラーが発生した場合はコメントかメールでお知らせいただけると助かります。

Python 3.6, matplotlib 2.1.1, pyFAI 0.17, Jupyter notebookを使っています。この記事で使うライブラリと関数は以下です。

import numpy as np
import matplotlib.pyplot as plt
# ver 0.16.0からは import pyFAI ではなく以下推奨
from pyFAI.azimuthalIntegrator import AzimuthalIntegrator
from pyFAI.detectors import Detector
# from pyFAI import version as pyfaiversion
# print(pyfaiversion) # バージョン情報を知りたい場合

# 説明用のグラフを整えるための道具
from mpl_toolkits.axes_grid1 import ImageGrid
from matplotlib.ticker import MultipleLocator, LogLocator
from matplotlib.lines import Line2D
from matplotlib.patches import Wedge, Polygon, Rectangle
from matplotlib.colors import LogNorm

np.random.seed(100) # 乱数の再現性をだすためにseedを指定

# ビームセンターを原点としたピクセル座標を逆空間の座標(単位nm^-1)に変換する
def x2q(x, wv, dist, pixelsize):
    '''
    x: ビームセンターを原点としたピクセル座標
    wv: 入射ビームの波長 (nm)
    pixelsize: 検出器のピクセル辺の長さ (m)
    dist: 試料と検出器の間の距離(m)
    '''   
    return 4*np.pi/wavelength*np.sin(np.arctan(pixelsize*x/dist)/2)

# サンプルデータ用。ナノ粒子からのSANS散乱断面積を計算
def Sphere(Q, particle_size, eta=1):
    vol = 4/3*particle_size**3
    qr = Q*particle_size
    return (vol*eta*3*(np.sin(qr)-qr*np.cos(qr))/qr**3)**2

# Sphere関数で作ったデータに異方性を持たせる
def Sin2(data, chi):
    # data and chi are numpy 2d arrays with same shape
    # theta in radian
    return data*np.sin(chi*2)**2

ver 0.15.0まではimport pyFAIとするのがドキュメントにも書いてある作法でしたが、これだと必要のない機能なども含めたパッケージ全体を読み込むことになりimportに数秒がかかっていました。しかし、ver 0.16.0でパッケージの構成が整理されたことで、上記のように必要なものだけを読み込みやすくなりimportにかかる時間がかなり短縮されました。

テストデータ準備

等方的データ

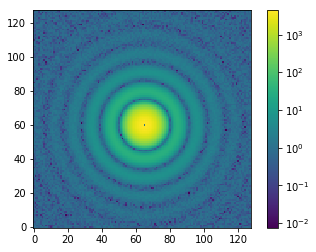
よくあるタイプの方向依存性のないデータを用意します。pyFAIは一次元化の際に横軸の数値の単位を$\mathrm{nm}^{-1}$, $\mathring{\mathrm{A}}^{-1}$, degree, radianのいずれかに設定します。装置関係のパラメータも含めて現実的な数字を使って説明したいので、先ほど定義したナノ粒子のSANS散乱断面積を求める関数Sphereを使ってテストデータを作成します。中心にでてきてしまうnanには適当な値を代入しておきます。実際の測定データでは中心部には透過ビームの強度があります。小角散乱の強度のスケールは数桁にわたるので、Logスケールで表示するためにimshowのnormオプションを使い、colorbarのtickの配置にはLogLocatorを使っています⁶。

# 装置関連パラメータ。単位に注意。
detsize = 128 # 検出器の一片のピクセル数
dist = 4 # 試料から検出器までの距離 (m)
bc = (65, 60) # ビームセンター。numpy arrayの行列座標ではなく、extentなしでimshowしたときのxy座標
pixelsize = 0.0075 # 検出器のピクセルの実寸 (m)
wavelength = 0.4 # 入射ビームの波長 (nm)

X, Y = np.meshgrid(range(detsize), range(detsize))

R = np.sqrt((X - bc[0])**2 + (Y - bc[1])**2)*pixelsize # ビームセンターからの各ピクセルまでの距離 (m)
chi = np.arctan2((Y-bc[1]), (X-bc[0])) # アジマス角 (radian) dataの計算には不要だが後ほどプロットする
# np.arctan2((X-bc[0]), (Y-bc[1]))ではないことに注意
phi = np.arctan(R/dist) # 試料から散乱されたビームが透過した場合からずれた角度 (radian)
Q = 4*np.pi/wavelength*np.sin(phi/2) # 散乱ベクトル (nm^-1)
data = Sphere(Q, particle_size, eta=0.05) + np.random.rand(detsize, detsize) # 実際の測定データの様子に近づけるためのバックグラウンドノイズを加える
data[np.isnan(data)] = 1 # NaNを適当な値で置換

fig, ax = plt.subplots()
img = ax.imshow(data, origin='lower', norm=LogNorm())
cbar = fig.colorbar(img, ticks=LogLocator())

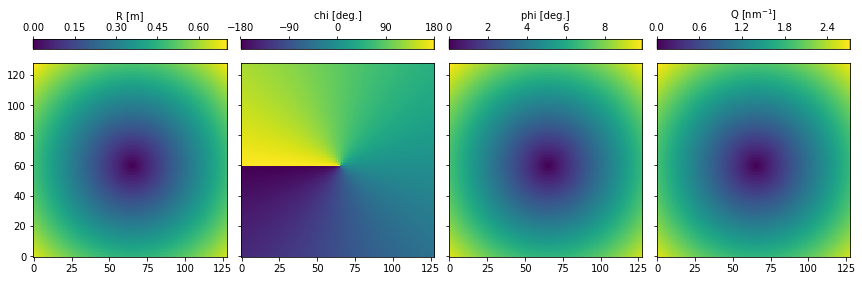
計算途中にでてきたR, chi, phi, Qは全て検出器と同じサイズの二次元numpy arrayです。検出器の各ピクセルが小角散乱のジオメトリーにおいてどういう位置にあるかを示しています。notationは「小角散乱のジオメトリー」の図と同じです。imshowを並べてcolorbarをつけたいときはplt.subplotsよりもImageGridが圧倒的に便利です(サンプルコード) 。

fig = plt.figure(figsize=(16,4))
grid = ImageGrid(fig, 111, nrows_ncols=(1, 4), axes_pad=0.20, share_all=True, label_mode="L",
                 cbar_location="top", cbar_mode="each",)
titles = ['R [m]', 'chi [deg.]', 'phi [deg.]', 'Q [nm$^{-1}$]']
zs = [R, chi/np.pi*180, phi/np.pi*180, Q]

for ax, cax, z, title in zip(grid, grid.cbar_axes, zs, titles):
    im = ax.imshow(z, origin='lower')
    if 'chi' in title:
        cbar = cax.colorbar(im, ticks=MultipleLocator(90))
    else:
        cbar = cax.colorbar(im)
    cbar.set_label_text(title)

異方的データ

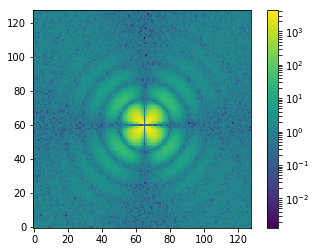
integrate_radialのデモ用に異方性のあるデータも作ります。上で作った等方的なdataに四回回転対称を持たせる関数Sin2を適用するだけです。ここでもnanをなくすために適当な値を足しています。imshowで図示すると四つの節を持っていることがわかります⁷。

data_aniso = Sin2(data, chi) + np.random.rand(detsize, detsize)

fig, ax = plt.subplots()
img = ax.imshow(data_aniso, origin='lower', norm=LogNorm())
fig.colorbar(img)

0カウントピクセルとBG差し引き後の負ピクセルの可視化時の扱い

logスケールでの可視化をする際には0と負の値が気になります。norm=LogNorm()はこれらの値をNaNにして良きに計らってくれます。大抵のカラーマップの場合はNaNは透明になると思いますが、cmap.set_badメソッドやNaNを最小値に置換するなどして調整もできます。詳細はこちらの解説を参照してください。

pyFAIパラメータ設定

等方データ作成の時に定義した検出器距離などの装置関連パラメータをAzimutalIntegratorオブジェクトに渡します。

detector = Detector(pixel1=pixelsize, pixel2=pixelsize)
ai = AzimuthalIntegrator(dist=dist, detector=detector, wavelength=wavelength*1e-9)
# チュートリアルにあるpixel1, 2オプションは廃止予定。Detectorオブジェクト経由で指定する。

rbin, azbin = 80, 360 # 動径方向と角度方向に一次元化したときののデータ点の数。計算上はrebinningする際のbinの数。

ai.setFit2D(dist*1000, *(bc+np.array((0.5, 0.5)))) # distance は milimeter
# setFit2DはaiのBaseであるGeometryクラスのメソッド
# poni形式ではなく、ビームセンターの座標を基準にジオメトリーを決めるFIT2D形式

前提知識の項目で述べた通り、pyFAIのピクセル座標の定義に合わせるためビームセンターの座標に0.5を足している点に注意してください。

integrate1d

dth = 15 # アジマス角の幅
q, I = ai.integrate1d(data, npt=rbin, azimuth_range=(0-dth, 0+dth)) # アジマス角の単位はdegree
ai.setChiDiscAtZero() # azimuth_rangeを適用する際に使われるアジマス角データ ai.chiArrayの不連続線を0度へ
q1, I1 = ai.integrate1d(data, npt=rbin, azimuth_range=(180-dth, 180+dth))
ai.setChiDiscAtPi() # 不連続線をデフォルトの180度へ戻す

横軸が検出器上の動径方向の単位($\mathrm{nm}^{-1}$, $\mathring{\mathrm{A}}^{-1}$, degree, radian)になるような一次元化データを計算します。方向と中心からの距離で特定の領域を指定することもできますし、何も指定しなければ全周平均を計算してくれます。AzimuthalIntegratorオブジェクトに正しいパラメータを設定していれば1行で終わります。ここでは比較のために0度方向と180度方向$\pm$15度の領域の一次元データを計算しています。現在の仕様では180度を含む領域を指定する場合はアジマス角の不連続線の位置に注意する必要があります。詳しくは後ほど述べます。オプションの種類は公式ドキュメントを見てください。計算したデータをファイルに保存したい場合はfilenameオプションを使うだけです。

以下は全てグラフの作成に関するコードです。大したことはしていませんが、matplotlibで作ったグラフを構成する基本要素について理解していないと何をしているかわからない部分があると思います。

# imshowした際にextentオプションを使ってx軸y軸をnm^-1にする
qx = x2q(np.arange(detsize)-bc[0], wavelength, dist, pixelsize)
qy = x2q(np.arange(detsize)-bc[1], wavelength, dist, pixelsize)
extent = [qx.min(), qx.max(), qy.min(), qy.max()]

fig, axes = plt.subplots(1,2, figsize=(10, 4), gridspec_kw={'width_ratios':[3, 2]})
fig.suptitle('integrate1d', y=1.07, fontsize=15)

Q1d = np.linspace(0.03, 2, 100) # nm-1 比較用Sphere関数で使う
labels = ['0$\pm{}^\circ$'.format(dth), '180$\pm{}^\circ$'.format(dth),
          'Sphere(Q, R)', '1D slice of 2D data'] # legend用ラベル
axes[0].loglog(q, I, q1, I1,
               Q1d, Sphere(Q1d, particle_size, eta=0.05) + np.random.rand(100),
               Q[65, bc[0]:], data[65, bc[0]:], marker='.')
axes[0].legend(labels=labels)
axes[0].set(xlabel='Q (nm$^{-1}$)', ylabel='Intensity', title='Sector integration of\nisotropic SANS intensity')

axes[1].imshow(SafeLog10(data), extent=extent , origin='lower')
axes[1].yaxis.set_major_locator(MultipleLocator(1))
axes[1].set(xlabel='Qx (nm$^{-1}$)', ylabel='Qy (nm$^{-1}$)', title='Integration ranges')

# 積分範囲を示す図形を追加
# 複数のpatchを追加するには一つずつadd_patchするよりlistにまとめてPatchCollectionで追加した方が描画効率が良い
# https://matplotlib.org/api/collections_api.html#matplotlib.collections.PatchCollection
height = lambda q: np.tan(dth/180*np.pi)*(q)
polycoord = lambda x: np.array([[0, 0], [x, height(x)], [x, -height(x)]])
patches = [Polygon(polycoord(qx.max()), closed=True, color='C0'),
           Polygon(polycoord(qx.min()), closed=True, color='C1')]
# ax.add_collectionメソッドは軸に表示されている座標(transData)を使ってくれる
axes[1].add_collection(PatchCollection(patches, match_original=True, alpha= 0.7, edgecolor='w'))

# 1D slice of 2D dataの抽出範囲を示す線を追加
# ax.add_lineメソッドも同様に軸に表示されている座標がデフォルト
axes[1].add_line(Line2D([0, qx.max()], [0, 0], lw=2, color='C3'))

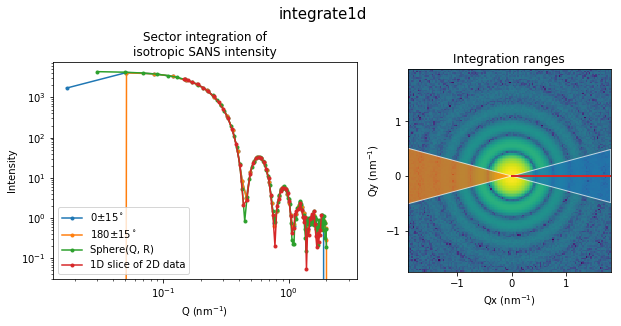
integrate1dで積分した0度と180度方向の一次元化データに加えて、データ作成に使ったSphere関数と二次元データから0度方向に相当する行を抽出したデータも一緒にプロットしました。すべて一致していることがわかります⁸。

アジマス角の不連続性に注意

azimuth_rangeオプションで指定したアジマス角の範囲が180度を含む時はアジマス角の不連続性に注意する必要があります。azimuth_rangeが指定された場合、ai.integrate1dは検出器の各ピクセルのアジマス角を表現するnumpy arrayを使って指定範囲内にある領域を抽出します。アジマス角のデフォルトは$-\pi$から$\pi$に設定されているため、このアジマス角arrayには180度に不連続な線が生じます。ai.setChiDiscAtZero()を実行するとアジマス角の範囲が0から$2\pi$に変更されこの不連続な線は0度に移動します。この様子は設定されている不連続線の位置でアジマス角arrayを生成するai.chiArray()を使って可視化するとよくわかります。

fig, axes = plt.subplots(1, 3, figsize=(7, 3), gridspec_kw=dict(width_ratios=(1, 1, 0.05)))
ai.setChiDiscAtPi()
img = axes[0].imshow(ai.chiArray(), origin='lower')
ai.setChiDiscAtZero()
axes[1].imshow(ai.chiArray(), origin='lower')
fig.colorbar(img, cax=axes[2])
axes[0].set_title('ai.setChiDiscAtPi(), default')
axes[1].set_title('ai.setChiDiscAtZero()')
ai.setChiDiscAtPi() # 元に戻す

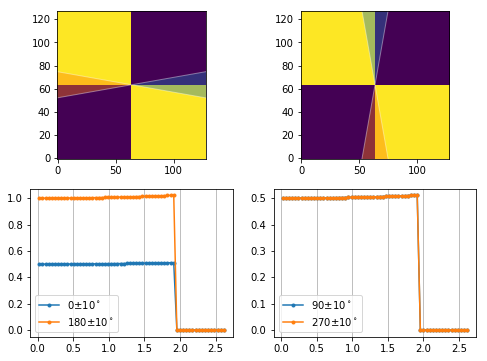
この不連続線を考慮せずに180度を含む範囲を指定すると、実は180度以上の範囲が無視されてしまいます。通常、あるアジマス角範囲内の積分をとるのは、その範囲の中で散乱の様子が同じだからであり、このとき一部が無視されても積分の結果には目立った変化がないためなかなか無視されてしまっていることに気づきません。しかし、以下のような180度を境に数字が全く異なるデータで試すと無視されていることがよくわかります。以下の例では青とオレンジで表される0、90、180、270度の各方向の一次元データが同じになることを期待してプロットしていますが、180度を含む範囲の場合は180度以降が無視されています。

data_fake = np.zeros((128, 128))
data_fake[0:64, 64:128] = 1
data_fake[64:128, 0:64] = 1

bc_pix = (63.5, 63.5) # ビームセンターは0-127の真ん中　
ai.setFit2D(dist*1000, *(bc_pix + np.array((0.5, 0.5)))) # ビームセンターを定義し直す

ths = [0, 90]
fig, axes = plt.subplots(2, len(ths), figsize=(4*len(ths), 3*2))
dth = 10

for th, ax, ax1 in zip(ths, axes[0], axes[1]):
    thmin, thmax = th-dth, th+dth
    q, I = ai.integrate1d(data_fake, npt=rbin, azimuth_range=(thmin, thmax)) # azimuthal angle unit in degree
    q1, I1 = ai.integrate1d(data_fake, npt=rbin, azimuth_range=(thmin+180, thmax+180))
    ax.imshow(data_fake, origin='lower')
    ax.add_patch(Wedge(bc_pix, 90, thmin, thmax, alpha=0.4, facecolor='C0', edgecolor='w'))
    ax.add_patch(Wedge(bc_pix, 90, thmin+180, thmax+180, alpha=0.4, facecolor='C1', edgecolor='w'))
    lines = ax1.plot(q, I, '.-', q1, I1, '.-')
    ax1.legend(lines, [f'{th}$\pm${dth}$^\circ$', f'{th+180}$\pm${dth}$^\circ$'])
    ax1.grid(axis='x', which='both')

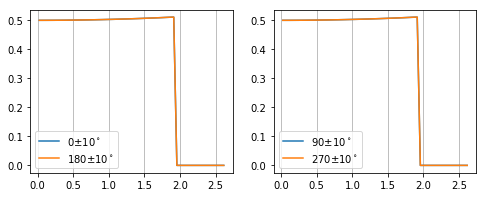
期待通りの結果を得るには、azimuth_rangeが180度を含むか含まないかによってアジマス角の不連続線の位置を変える必要があります。

fig, axes = plt.subplots(1, len(ths), figsize=(4*len(ths), 3*1))
for th, ax, in zip(ths, axes):
    for offset in [0, 180]:
        thmin, thmax = th-dth+offset, th+dth+offset
        if (thmin < 180 and thmax > 180):
            ai.setChiDiscAtZero()
        else:
            ai.setChiDiscAtPi() # デフォルト
        q, I = ai.integrate1d(data_fake, npt=rbin, azimuth_range=(thmin, thmax)) # azimuthal angle unit in degree
        line, = ax.plot(q, I, label=f'{th+offset}$\pm${dth}$^\circ$')
    ax.legend()
    ax.grid(axis='x', which='both')

ai.setChiDiscAtPi() # デフォルトに戻す
ai.setFit2D(dist*1000, *(bc+np.array((0.5, 0.5)))) # ビームセンターも元に戻す

この対処方法はアジマス角範囲が180度以下（扇型の中心角が鋭角）の場合に有効です。必要な場面はほとんどないと思いますが、アジマス角範囲に0度と180度の両方が含まれる場合はもう少し面倒な対処をしないといけません。
また、非常にややこしくなるので用が済んだらデフォルト設定に戻すことを忘れないようにした方が良いでしょう。

Integrate1dResultオブジェクト

上の例ではai.integrate1dが返す値をq, Iで受け取っていますが、これは実はback compatibilityのために残されている省略記法です。本来返されるオブジェクトはIntegrate1dResultであり、上の例でのqやIに相当する数値は

res = ai.integrate1d(data, npt=rbin, azimuth_range=(0-dth, 0+dth))
# resがIntegrate1dResult 
q = res.radial
I = res.intensity

としても得ることができます。

Integrate1dResultのdocstringを見ると、他にも見れる属性があるようです。

Result of an 1D integration. Provide a tuple access as a simple way to reach main attrbutes.
Default result, extra results, and some interagtion parameters are available from attributes.

For compatibility with older API, the object can be read as a tuple in different ways:

.. codeblock::

    result = ai.integrate1d(...)
    if result.sigma is None:
        radial, I = result
    else:
        radial, I, sigma = result

属性やメソッドを取得する関数を以下のように定義してどんな属性を持っているか調べてみます。

def PrintMethodsAndAttributes(obj, public=True):
    result = {}
    for x in dir(obj):
        if public:
            if not x[0] is '_':
                result[x] = type(getattr(obj, x))
        else:
            result[x] = type(getattr(obj, x))
            
    return result

res = ai.integrate1d(data, npt=rbin, azimuth_range=(0-dth, 0+dth), method=method)

print(type(res))

for k, v in PrintMethodsAndAttributes(res).items():
    print('{:20}{}'.format(k, v))

output

<class 'pyFAI.containers.Integrate1dResult'>
compute_engine      <class 'str'>
count               <class 'numpy.ndarray'>
has_dark_correction <class 'bool'>
has_flat_correction <class 'bool'>
has_mask_applied    <class 'bool'>
index               <class 'builtin_function_or_method'>
intensity           <class 'numpy.ndarray'>
metadata            <class 'NoneType'>
method_called       <class 'str'>
normalization_factor<class 'float'>
npt_azim            <class 'NoneType'>
percentile          <class 'NoneType'>
polarization_factor <class 'NoneType'>
radial              <class 'numpy.ndarray'>
sigma               <class 'NoneType'>
sum                 <class 'numpy.ndarray'>
unit                <class 'pyFAI.units.Unit'>

どうやら計算結果の他には計算に使ったオプションの情報を持っているようです。

integrate_radial

qranges = [(0.2, 0.8), (1, 2)] # in nm^-1
chi, I = ai.integrate_radial(data_aniso, npt=azbin, radial_range=qranges[0])
chi1, I1 = ai.integrate_radial(data_aniso, npt=azbin, radial_range=qranges[1])

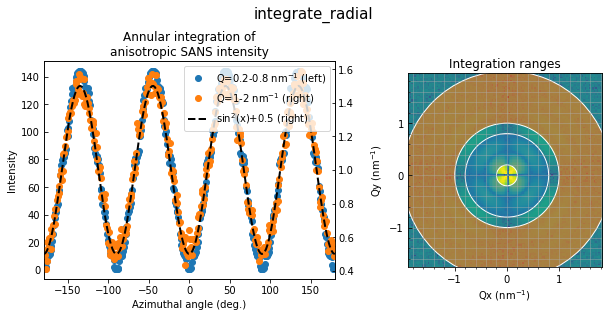
横軸がアジマス角になるようなプロットです。これも1行で終わります。あとは全てグラフ作成部分です。

qx = x2q(np.arange(detsize)-bc[0], wavelength, dist, pixelsize)
qy = x2q(np.arange(detsize)-bc[1], wavelength, dist, pixelsize)
extent = [qx.min(), qx.max(), qy.min(), qy.max()]

fig, axes = plt.subplots(1,2, figsize=(10, 4), gridspec_kw={'width_ratios':[3, 2]})
plt.subplots_adjust(wspace=0.3)
fig.suptitle('integrate_radial', y=1.07, fontsize=15)

# formatする文字列内のLaTeX表記用の{}はもう一度{}で囲む
axes[0].plot(chi, I, 'o', c='C0', label='Q={}-{} nm$^{{-1}}$ (left)'.format(*qranges[0]))
axes[0].set(xlabel='Azimuthal angle (deg.)', ylabel='Intensity', xlim=(-180, 180), title='Annular integration of\nanisotropic SANS intensity')
axes[0].yaxis.get_major_formatter().set_powerlimits((-3, 3))

ax2 = axes[0].twinx()
ax2.plot(chi1, I1, 'o', c='C1', label='Q={}-{} nm$^{{-1}}$ (right)'.format(*qranges[1]))
x = np.linspace(-180, 180, 200)
ax2.plot(x, np.sin(2*x/180*np.pi)**2+0.5, c='k', lw=2, ls='dashed', label='$\sin^2$(x)+0.5 (right)')
axpos = axes[0].get_position()
fig.legend(loc='upper right', bbox_to_anchor=(axpos.x1, axpos.y1), bbox_transform=fig.transFigure)

axes[1].imshow(SafeLog10(data_aniso), extent=extent, origin='lower')
axes[1].minorticks_on()
axes[1].yaxis.set_major_locator(MultipleLocator(1))
axes[1].grid(True, which='both', alpha=0.5) # 円環の位置を確認するためのgrid
axes[1].set(xlabel='Qx (nm$^{-1}$)', ylabel='Qy (nm$^{-1}$)', title='Integration ranges')

patches = []
for i, (qmin, qmax) in enumerate(qranges):
    patches.append(Wedge((0, 0), qmax, 0, 360, width=qmax-qmin, alpha=0.6, color='C{}'.format(i)))
    
axes[1].add_collection(PatchCollection(patches, match_original=True, edgecolor='w')) 

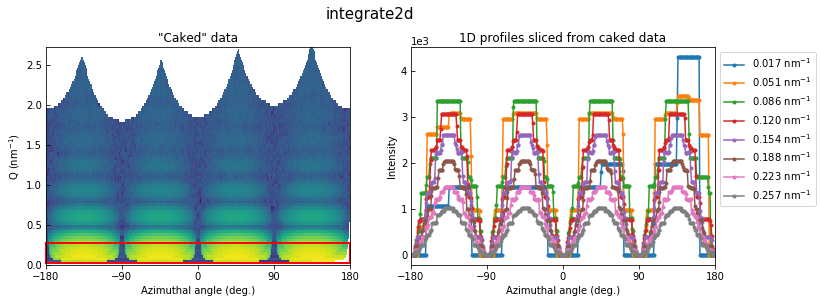
integrate2d

I, q, chi = ai.integrate2d(data_aniso, rbin, azbin)
print('azbin, rbin:', azbin, rbin)
print(I.shape)

output

azbin, rbin: 360 80
(360, 80)

これも1行で済みます。360度を1度刻み、中心からの距離で80分割してみました。

fig, axes = plt.subplots(1,2, figsize=(12, 4))
fig.suptitle('integrate2d', y=1.02, fontsize=15)

extent = [chi.min()-0.5, chi.max()-0.5, q.min(), q.max()]

axes[0].imshow(SafeLog10(I.T), origin='lower', extent=extent, aspect='auto')
axes[0].xaxis.set_major_locator(MultipleLocator(90))
axes[0].set(xlim=(-180, 180), ylim=(0, q.max()), xlabel='Azimuthal angle (deg.)', ylabel='Q (nm$^{-1}$)', title='"Caked" data')

axes[1].plot(chi, I[:, :8], '.-')
labels = ['{:.3f} nm$^{{-1}}$'.format(p) for p in q[:8]]
axes[1].xaxis.set_major_locator(MultipleLocator(90))
axes[1].set(xlim=(-180, 180), xlabel='Azimuthal angle (deg.)', ylabel='Intensity', title='1D profiles sliced from caked data')
axes[1].yaxis.get_major_formatter().set_powerlimits((-3, 3))
axes[1].legend(labels=labels, bbox_to_anchor=(1,1))

rect = axes[0].patches.append(Rectangle((chi[0], q[0]), 360, q[7], lw=2, ec='r', fill=False, transform=axes[0].transData))

左図の赤で囲まれた中心近傍の角度依存性を右図に示しました。80分割したうちの中心付近からの8個分の角度依存データに相当します。当然のことながら、ピクセルの少ない中心部分は360分割しても同じピクセル内に止まっている部分が大半であることがわかります。

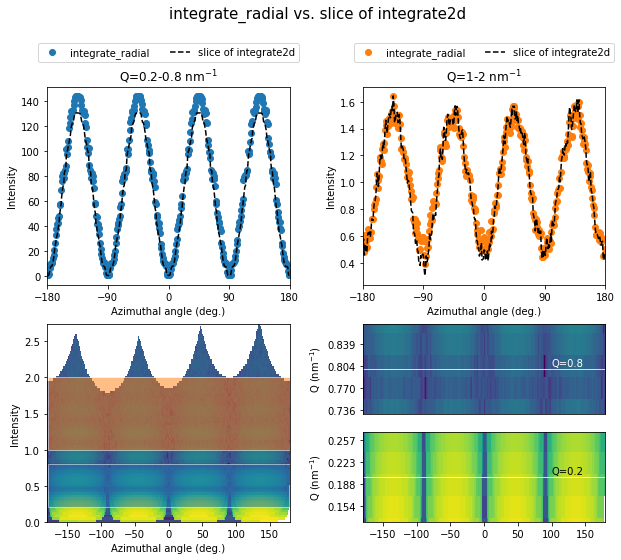
integrage_radialとintegrate2dのスライスの比較

角度依存データはintegrate_radialとintegrate2dの二つの方法で得られることがわかりましたが、両者を比べて見るとintegrate_radialのほうが角度依存性のあるデータを可視化する上で適切な処理をしていることがわかります。

qranges = [(0.2, 0.8), (1, 2)] # in nm^-1
chi, I = ai.integrate_radial(data_aniso, npt=azbin, radial_range=qranges[0])
chi1, I1 = ai.integrate_radial(data_aniso, npt=azbin, radial_range=qranges[1])

fig, axes = plt.subplots(1,2, figsize=(10,4), subplot_kw=dict(xlim=(-180, 180), xlabel='Azimuthal angle (deg.)', ylabel='Intensity'))
fig.suptitle('integrate_radial vs. slice of integrate2d', y=1.02, fontsize=15)

axes[0].plot(chi, I, 'o', c='C0', label='integrate_radial')
axes[0].yaxis.get_major_formatter().set_powerlimits((-3, 3))
axes[0].xaxis.set_major_locator(MultipleLocator(90))
axes[0].set_title('Q={}-{} nm$^{{-1}}$'.format(*qranges[0]))

axes[1].plot(chi1, I1, 'o', c='C0')
axes[1].xaxis.set_major_locator(MultipleLocator(90))
axes[1].set_title('Q={}-{} nm$^{{-1}}$'.format(*qranges[1]))

I, q, chi = ai.integrate2d(data_aniso, rbin, azbin)

cond = (q >= qranges[0][0]) & (q <= qranges[0][1])
axes[0].plot(chi, I[:, cond].sum(axis=1)*(q[1]-q[0]), 'o', c='C1', label='slice of integrate2d')

cond = (q >= qranges[1][0]) & (q <= qranges[1][1])
axes[1].plot(chi, I[:, cond].sum(axis=1)*(q[1]-q[0]), 'o', c='C1')

fig.legend(bbox_to_anchor=(1, 1), bbox_transform=axes[0].transAxes)

integrate2dでは極座標で展開する際にはpixel splittingが考慮されていますが、展開後のデータから特定のQレンジのデータを抽出する際にはnumpy arrayのslicingだけでは合算しそこねてしまう強度がでてきます（右下図参照）。上の例では左上図のQ=0.2-0.8に$\sin^2(\chi)$のピークトップの差としてその影響がでていると思われます。また、右上図のQ=1-2の例では、integrate2dで検出器がカバーしていない白い領域（左下図）の影響が谷の差として現れています。もちろんこれらは適当な規格化をすれば解決できる話ですが、numpy arrayのslicing以上のことをするのは正直いって少し面倒です。integrate_radialではQレンジを抜き出す際にpixel splittingが適用され、検出器がカバーしていない領域も考慮して規格化された強度が計算されているため、面倒な計算をせずに比較に使える数値が得られます。

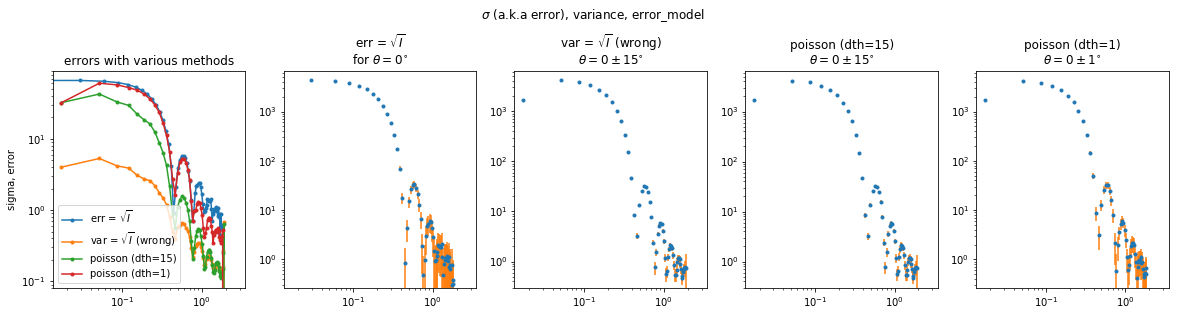
varianceまたはerror_modelオプションを使った伝搬誤差の計算

pyFAIには伝搬誤差を計算するために分散を指定するvarianceオプションがあります。規格化や平均などの操作をしていない生データの場合はerror_modelオプションを使うこともできます。varianceで指定するのは分散であり統計誤差ではないので注意が必要です。例えば、検出器による放射線のカウント数はPoisson統計に従うとされており、あるカウント数$I$が検出された時の標準誤差⁹$\sigma$は、$I$を検出数分布の平均値と仮定して$\sigma=\sqrt{I}$となります。このとき分散は$\sigma^2=I$です。規格化や平均などの操作をしたデータのpyFAI内での伝搬誤差が欲しい場合は、規格化や平均による伝搬誤差の二乗をvarianceに指定します。強度の平方根から直接誤差を計算した場合とpyFAIの誤差伝搬オプションを使った場合の比較を以下に示します。

err = np.sqrt(data)
errkws = [dict(variance=err), dict(error_model='poisson'), dict(error_model='poisson')]
labels = ['var = $\sqrt{I}$ (wrong)', 'poisson (dth=15)', 'poisson (dth=1)']

fig, axes = plt.subplots(1, 5, figsize=(20,4), subplot_kw=dict(yscale='log', xscale='log'))
fig.suptitle('$\sigma$ (a.k.a error), variance, error_model', y=1.1)

axes[0].plot(Q[bc[1], bc[0]:], err[bc[1], bc[0]:], marker='.', label='err = $\sqrt{I}$')

axes[1].errorbar(Q[bc[1], bc[0]:], data[bc[1], bc[0]:], err[bc[1], bc[0]:], marker='.', ls='none', ecolor='C1')
axes[1].set_title('err = $\sqrt{I}$\nfor $\\theta=0^{\circ}$')

for errkw, ax, label in zip(errkws, axes[2:].ravel(), labels):
    if '(dth=1)' in label:
        dth = 1
    else:
        dth = 15
    res = ai.integrate1d(data, npt=rbin, azimuth_range=(0-dth, 0+dth), **errkw)
    axes[0].plot(res.radial, res.sigma, marker='.', label=label)
    ax.errorbar(res.radial, res.intensity, res.sigma, marker='.', ls='none', ecolor='C1')
    ax.set_title(label + '\n$\\theta=0\pm{}^{{\circ}}$'.format(dth))

axes[0].set_title('errors with various methods')
axes[0].set_ylabel('sigma, error')
axes[1].set_xlim(ax.get_xlim())
axes[1].set_ylim(ax.get_ylim())
# axes[0].set_ylim(res.intensity.min()*0.95, res.intensity.max()*1.05)
    
axes[0].legend()

一番左の図は各方法で求めた誤差の大きさを比較しています。左から2番目のerr=$\sqrt{I}$では$\theta=0^{\circ}$に相当するnumpy arrayの1行分のデータに強度の平方根をエラーバーとしてつけています。右三つがpyFAIによる伝搬誤差の例です。var=$\sqrt{I}$はvarianceに誤差を渡してしまう間違いの例で、一番左のプロットにある通りこの場合qが小さい領域で誤差が小さく見積もられてしまいます。右側二つは積分領域の異なるerror_model='poisson'の例です。積分領域の大きいdth=15の方が誤差が改善されています。一方dth=1の例はnumpy array1行分のデータに近くなっています。実際、一番左のプロットで誤差の大きさを比較すると、pyFAIで切り取っている扇型（三角）の広がりによる積分の効果が出てくるhigh q領域以外はほぼ誤差の大きさが一致しています。

methodオプションの比較

pixel splittingに関する手法を指定するmethodオプションも比較してみます。各手法の具体的な違いについては何も調べていません。単純に実行時間と結果を比較します。

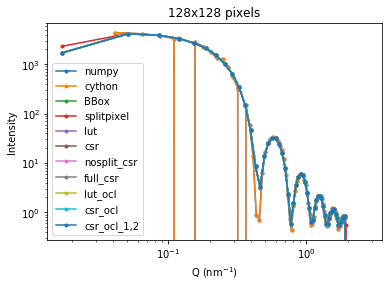
128x128ピクセルの場合

まずはこれまで扱ってきた128x128ピクセルのデータをみてみます。

dth = 15
methods = ['numpy', 'cython', 'BBox', 'splitpixel', 'lut', 'csr', 'nosplit_csr', 'full_csr']
methods_gpu = ['lut_ocl', 'csr_ocl', 'csr_ocl_1,2']

qx = x2q(np.arange(detsize)-bc[0], wavelength, dist, pixelsize)
qy = x2q(np.arange(detsize)-bc[1], wavelength, dist, pixelsize)
dq = qx[1]-qx[0]
extent = [qx.min()-dq/2, qx.max()+dq/2, qy.min()-dq/2, qy.max()+dq/2]

ax = plt.gca()
ax.set(xlabel='Q (nm$^{-1}$)', ylabel='Intensity', 
       title='B')

for method in methods+methods_gpu:
    start = time()
    q, I = ai.integrate1d(data, npt=rbin, azimuth_range=(0-dth, 0+dth), method=method)
    print('{:15}{:.3f}ms'.format(method, (time()-start)*10**3))
    ax.loglog(q, I, marker='.', label=method)

ax.legend()

output

numpy          0.894ms
cython         0.705ms
BBox           0.826ms
splitpixel     0.760ms
lut            0.354ms
csr            0.443ms
nosplit_csr    0.331ms
full_csr       0.310ms
lut_ocl        0.863ms
csr_ocl        0.625ms
csr_ocl_1,2    0.663ms

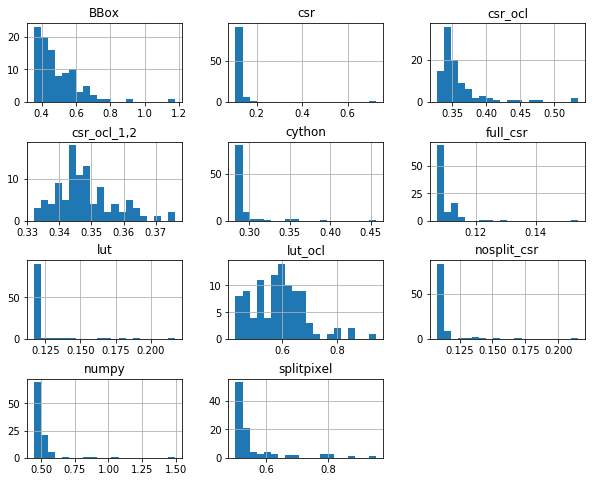
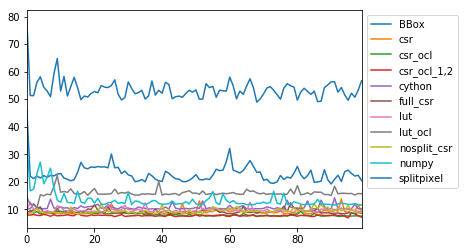
methods='cython'だけ妙な振る舞いをしていますが、他はqの値が若干異なるだけでほぼ一致しています。実行時間をprintしましたが、実はこの値は実行するたびにかなり変動します。以下に各methodsを100回繰り返したときの実行時間のヒストグラムを示します。

from pandas import DataFrame
exctime = {}
temp = []
for method in methods+methods_gpu:
    for _ in range(100):
        start = time()
        q, I = ai.integrate1d(data, npt=rbin, azimuth_range=(0-dth, 0+dth), method=method)
        temp.append((time()-start)*10**3)
    exctime[method] = temp
    temp = []
exctime = DataFrame(exctime)


axes = exctime.hist(bins=20, figsize=(10, 8))
fig = plt.gcf()
fig.subplots_adjust(hspace=0.5)

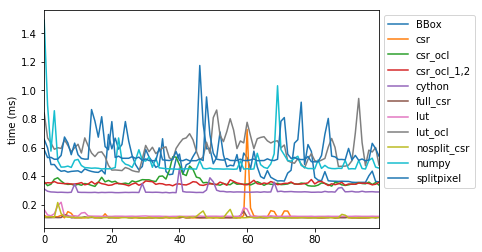
ax = exctime.plot(legend=False, )
ax.legend(loc='upper left', bbox_to_anchor=(1,1))
ax.set_ylabel('time (ms)')

デフォルトになっているmethod='csr'が安定して速いのがわかります。OpenCLでGPUを使うオプションは特に速くありません。この辺の原理はよく知らないので、知っている人からすると当然の結果なのかもしれません。

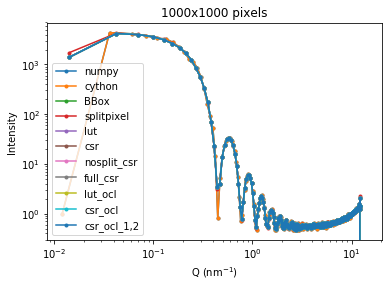
1000x1000ピクセルの場合

もっとメガピクセル級の検出器データの場合はどうでしょうか。dataとaiを変更して同じことをしてみます。

detsize = 1000 # num of pixels 
dist = 4 # distance between sample and detector in m
bc = (480, 505) # (x, y) position of the beam center in xy coordinate of imshow
pixelsize = 0.0075 # in m
wavelength = 0.4 # in nm

X, Y = np.meshgrid(range(detsize), range(detsize))

R = np.sqrt((X - bc[0])**2 + (Y - bc[1])**2)*pixelsize # distance from bc to pixels in m
chi = np.arctan2((Y-bc[1]), (X-bc[0])) # angle in radian. will be used later.
phi = np.arctan(R/dist)
Q = 4*np.pi/wavelength*np.sin(phi/2)
data_large = Sphere(Q, particle_size, eta=0.05) + np.random.rand(detsize, detsize)
data_large[np.isnan(data_large)] = 1 # replace nan with 0.1

detector = pyFAI.detectors.Detector(pixel1=pixelsize, pixel2=pixelsize)
ai = pyFAI.AzimuthalIntegrator(dist=dist, detector=detector, wavelength=wavelength*1e-9)
rbin, azbin = 500, 360 # rbin
ai.setFit2D(dist*1000, *(bc+np.array((0.5, 0.5)))) # distance in milimeter

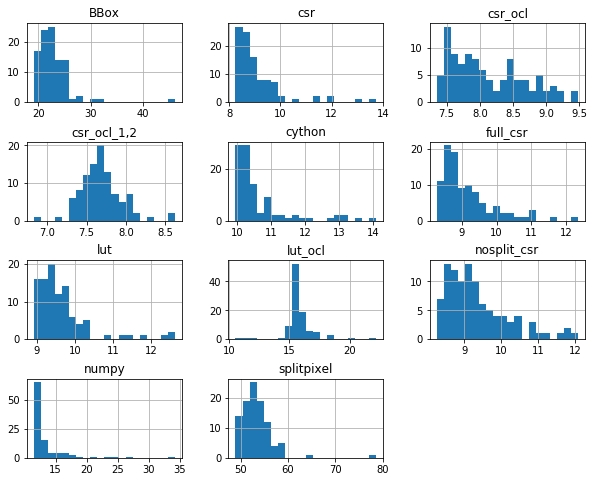
numpy          27.168ms
cython         19.527ms
BBox           49.702ms
splitpixel     85.091ms
lut            10.618ms
csr            11.129ms
nosplit_csr    11.597ms
full_csr       12.893ms
lut_ocl        13.299ms
csr_ocl        8.138ms
csr_ocl_1,2    7.281ms

バラつきがあるのは128x128のときと同じですが、ピクセルの数が多くなるとOpenCLを使ったcsr_oclとcsr_ocl_1,2が安定して速いようです。

1. 例えばこちらの解説では二次元検出器を使ったX線回折っぽいデータを作るのにarrayの要素ごとの極座標を計算しています。 ↩

2. 私が扱っているのはせいぜい1時間に3個くらい作成される128x128か256x256ピクセルのデータなのでOpenCLのオプションを使ったことはありませんが、1000x1000ピクセルレベルの高分解能データを扱う場合や1秒あたり数百〜数千個の二次元データが出力される自由電子レーザーなどの大強度ビームを使った測定では威力を発揮するはずです。 ↩

3. 脚注1と同じ解説の最後の図みたいなやつです。 ↩

4. 実はこの記事に出てくるグラフのコードもそらで書いたわけではなく、何度も公式ドキュメントを参照して仕上がったものです。 ↩

5. Pythonで測定データを解析する際の利点は、データの処理からグラフ作成まで一気にできる点です。しかし、これには「ただし、グラフの見た目の調整に時間がかかることが多い」という但し書きがつくべきだと私は思っています。matplotlibはPythonにおけるグラフ作成ライブラリのデファクトスタンダードとなっていて、日本語の情報も多いので基本的な設計概念を学ばずにウェブに散らばるレシピをその都度ググっているだけでも、同僚と結果を共有するレベルの用途ではそこまで困ることはないでしょう。しかし、このやり方だと論文や学会で発表できるレベルの見た目に仕上げる段階になって間違いなくつまずきます。締め切り直前にグラフの細かい調整方法をググりたおすのに時間をかけたくない方は是非 早く知っておきたかったmatplotlibの基礎知識、あるいは見た目の調整が捗るArtistの話 を読んでください。 ↩

6. LogNormを使っていれば自動的にLogスケールのtickがでてくることが多いのですが、なぜか出てこなかったのでLogLocatorを指定しています。 ↩

7. ここでは（なぜか）期待通りにLogLocatorを指定しなくてもLogNormであることから自動的にLogスケールのtickが付いています。LogNormではLogLocator(subs='all')が使われるのでminor tick（のふりをしているmajor tick）が表示されています。この振る舞いについての詳細はこの解説を参照してください。 ↩

8. 落ち込む部分が合っていないように見えますが、実際の測定データではこの構造は検出器の分解能によって畳み込まれてぼやけるのでこのレベルで十分一致していると言えます。 ↩

9. この辺の用語の使い方は分野によってまちまちのようです。プロットする時のエラーバーに使う数値のつもりですが、この表現が正しいか自信はありません。 ↩