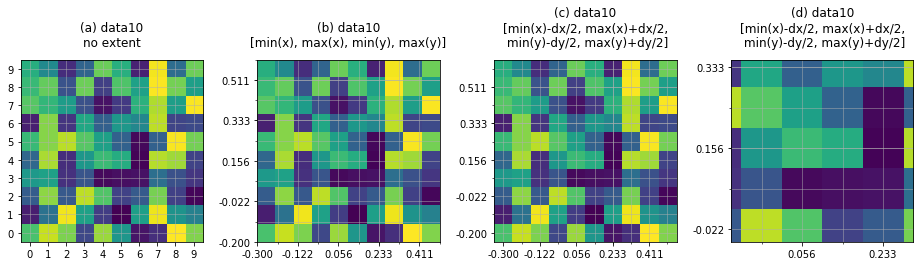matplotlibを使って二次元検出器の二次元強度マップを作るに引き続き、二次元検出器のデータ解析を念頭に置いた話ですが、NxNの2D numpy arrayを扱う際に気をつけるべき点とも言えるのでタイトルを少し一般的な表現にしました。
パッケージ
import numpy as np
import matplotlib.pyplot as plt
import pyFAI
# 軸の目盛り位置とラベル表示の調整用
from matplotlib.ticker import MultipleLocator, AutoMinorLocator
from matplotlib.ticker import StrMethodFormatter
pyFAIはEUの放射光施設である[ESRFのソフトウェアチームが開発] (http://www.esrf.eu/UsersAndScience/Publications/Highlights/2012/et/et3/)した極座標ベースのデータ抽出に使えるパッケージです。詳細は二次元データの一次元化に関する[別エントリ](https://qiita.com/skotaro/items/7c68012f85312332df8d)を参照してください。このエントリでは解析の際に座標の定義に気をつけるべき例に使います。condaのconda-forgeチャンネルから以下でインストールできます。
conda install -c conda-forge pyfai
方向に関する注意点
二次元検出器の測定データにまつわる様々な方向
物質科学で使われる二次元検出器から得られるのは、たいていの場合はデータの形(np.ndarray.shape)からは方向の区別がつかない正方形の二次元データです。強度分布がビームの中心に対して点対称な等方的データならば方向のことはあまり気にする必要はありませんが、角度依存性のある異方的データの場合は次のようなそれぞれ意味の異なる方向について考慮する必要があります。
- 試料、磁場や電場などの外場と検出器の物理的方向関係
- 検出器の物理的な方向と出力された二次元データの方向の関係
- 2D numpy arrayの中身を表示した際の行と列
- 2次元データを可視化する
contourf,imshow,pcolormeshなどにおける原点と正方向の定義 - 議論や発表の際に使う慣習的なx軸とy軸(または横軸と縦軸)
1と2はそれぞれの場合について実験者が自分で確認するしかないので、3と4及び両者のややこしい関係について例を使って説明して5の慣習的な表現とどう合わせていくか述べます1。
1D arrayと2D arrayの見た目とインデックスの関係を混同しない
- 1D arrayのインデックス
[i]は0始まりインデックスでi番目の要素を指す。 - 2D arrayのインデックス
[i,j]は0始まりインデックスでi行j列の要素を指す。
この二つの説明には特にわかりにくい部分はないと思いますが、jupyter notebook上で1D arrayと2D arrayを表示させて中身を確認しながら作業していると2D arrayのインデックスの順番をたまに間違えることがあります。以下に示す通り、1D arrayのdata[i]は中身を表示させた際の 水平方向のi番目 である一方で、2D arrayのdata[i,j]は中身を表示させた際の 垂直方向(=行)のi番目 、水平方向(=列)のj番目 だからです。
# 1D arrayのインデックス[i]はprint時の水平方向のi番目
data = np.zeros(5)
data[2] = 2
print(data)
[ 0. 0. 2. 0. 0.]
# 2D arrayのインデックス[i,j]はprint時の垂直方向のi行目、水平方向のj列目
data = np.zeros([10,10])
data[1] = 1
data[:,2] = 2
data[8,6] = 3 # 左上を[0,0]として8行目6列目の要素が3
print(data)
[[ 0. 0. 2. 0. 0. 0. 0. 0. 0. 0.]
[ 1. 1. 2. 1. 1. 1. 1. 1. 1. 1.]
[ 0. 0. 2. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 2. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 2. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 2. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 2. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 2. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 2. 0. 0. 0. 3. 0. 0. 0.]
[ 0. 0. 2. 0. 0. 0. 0. 0. 0. 0.]]
print(data[1]) # 行のみの指定
print(data[:,2]) # 列のみの指定
[ 1. 1. 2. 1. 1. 1. 1. 1. 1. 1.]
[ 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.]
例えば、ここで詳しくは述べませんが、私はよくX, Y = np.meshgrid(...)のXとYがiとjに対応してるという勘違いをしていました。どうも意図した挙動と違うなと気づいてもY, X = np.meshgrid(...)と書き換えて余計ことをややこしくしていました。
インデックス[i,j]と可視化時の(x,y)座標を混同しない
2D numpy arrayのインデックスは数学の行列と同じ定義なので、data[0,0]は中身を表示させた時の左上にあり、[i,j]のiの正方向は下でjの正方向は右です。ところで、dataの可視化の際は慣習的なx軸とy軸の正方向とiとjの正方向を合わせるために、data[0,0]が左下にくるように設定するのがよいでしょう。このとき(転置をしない限り2)、 data[i,j]のxy座標上の位置は(j,i) となります。これは、たとえば強度分布の重心を求める計算で出てできたインデックスベースの重心座標[i0, j0]を原点を左下にした2D arrayの上に重ねて表示して位置を確認したい時に、重心のxy座標を(j0, i0)としなければならないことを意味します。

contourf,pcolormesh,imshowにおける原点と方向の定義
以前の記事のimshowかpcolormeshか で書いたように一番速いimshowがおすすめなのですが、せっかくなのでimshowだけでなく他の二次元データ可視化関数のデフォルト設定で方向や原点の定義がどうなっているかも比較してみます。
fig, ax = plt.subplots(1,4, figsize=(20, 5))
plt.suptitle('contourf, pcolormesh, and imshow')
ax[0].contourf(data)
ax[0].set(aspect='equal', title='contourf(data)')
ax[1].pcolormesh(data)
ax[1].set(aspect='equal', title='pcolormesh(data)')
ax[2].imshow(data)
ax[2].set_title('imshow(data)')
ax[3].imshow(data, origin='lower')
ax[3].set_title("imshow(data, origin='lower')")
imshowを使ってdata[0,0]を慣習的な原点の位置である左下に設定するにはorigin='lower'オプションを使えばよいことがわかります。
座標に関する注意点
imshowにおけるピクセル座標の定義とextentによるピクセル座標ベースの拡大
私の実験屋のためのPythonシリーズでは二次元検出器のデータの可視化に描画処理の速いimshowを一貫して推奨していますが、imshowで測定データを拡大して詳しく調べたいときは、imshowのピクセル座標の定義とextentオプションの挙動について注意する必要があります。ここをきちんと押さえておかないと、拡大して詳しく調べたがゆえに解釈を間違ってしまう可能性もあります。
真ん中に十字のある10x10と128x128のテストデータで説明します。
data128 = np.zeros((128,128))
data10 = np.zeros((10,10))
data128[63:65] = [i for i in range(64)] + [i for i in range(63,-1, -1)]
data128[:, 63:65] = [[i] for i in range(64)] + [[i] for i in range(63, -1, -1)]
data10[4:6]=[i for i in range(5)] + [i for i in range(4, -1, -1)]
data10[:,4:6]=[[i] for i in range(5)] + `[[i] for i in range(4, -1, -1)]
# 中心部を拡大して表示します
print(data128[60:68, 60:68])
print(data10)
[[ 0. 0. 0. 60. 60. 0. 0. 0.]
[ 0. 0. 0. 61. 61. 0. 0. 0.]
[ 0. 0. 0. 62. 62. 0. 0. 0.]
[ 60. 61. 62. 63. 63. 62. 61. 60.]
[ 60. 61. 62. 63. 63. 62. 61. 60.]
[ 0. 0. 0. 62. 62. 0. 0. 0.]
[ 0. 0. 0. 61. 61. 0. 0. 0.]
[ 0. 0. 0. 60. 60. 0. 0. 0.]]
[[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 1. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 2. 2. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 3. 3. 0. 0. 0. 0.]
[ 0. 1. 2. 3. 4. 4. 3. 2. 1. 0.]
[ 0. 1. 2. 3. 4. 4. 3. 2. 1. 0.]
[ 0. 0. 0. 0. 3. 3. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 2. 2. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 1. 1. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
data10とdata128の強度分布(十字)の中心はインデックスベースの座標で表現するとそれぞれ[63.5 ,63.5]とです。座標の定義とextentの挙動の説明のために中心近傍の点を含めて以下のようなリストを用意します。
cen128 = [(63, 63), (63.5, 63.5), (64, 64)]
cen10 = [(4, 4), (4.5, 4.5), (5, 5)]
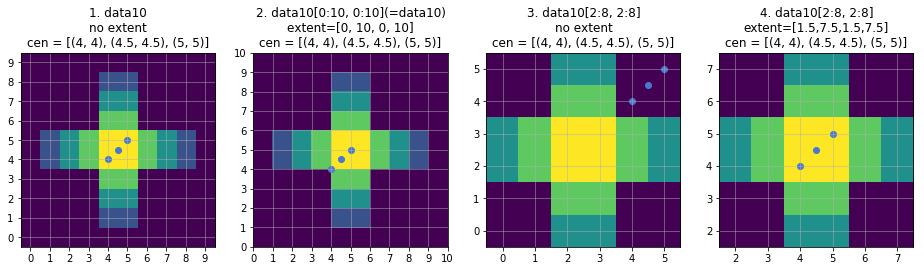
拡大とextentオプションの有無を変えて四通りの図を作るとimshowの座標の定義とextentの正しい設定の仕方がわかります。
fig, axes = plt.subplots(1,4, figsize=(16,4))
axes[0].imshow(data10, origin='lower')
axes[1].imshow(data10[0:10, 0:10], origin='lower', extent=[0, 10, 0, 10])
axes[2].imshow(data10[2:8, 2:8], origin='lower')
axes[3].imshow(data10[2:8, 2:8], origin='lower', extent=[1.5, 7.5, 1.5, 7.5])
titles= ['1. data10\nno extent\ncen = {}',
'2. data10[0:10, 0:10](=data10)\nextent=[0, 10, 0, 10]\ncen = {}',
'3. data10[2:8, 2:8]\nno extent\ncen = {}',
'4. data10[2:8, 2:8]\nextent=[1.5,7.5,1.5,7.5]\ncen = {}']
for ax, title in zip(axes, titles):
ax.grid(True, alpha=0.6)
ax.xaxis.set_major_locator(MultipleLocator(1))
ax.yaxis.set_major_locator(MultipleLocator(1))
ax.set_title(title.format(cen10))
ax.scatter(np.array(cen10)[:, 0], np.array(cen10)[:, 1])
四つの図からそれぞれ以下のことがわかります。
- 全データ表示、
extentなし
-
imshowのピクセル座標はピクセルの中央である
- 全データ表示、
extentあり(表示範囲のインデックスをそのまま指定するありがちな間違い)
-
extentオプションは図の両端の値を設定 -
ax.scatterはextentオプションで調整された軸の値を使う
- 拡大あり、
extentなし
-
extentを指定しないと、軸は常に0始まりインデックス
- 拡大あり、
extentあり(推奨)
- slicingに使っているインデックスより0.5小さい値を
extentに指定すると1を正しく拡大した図になる
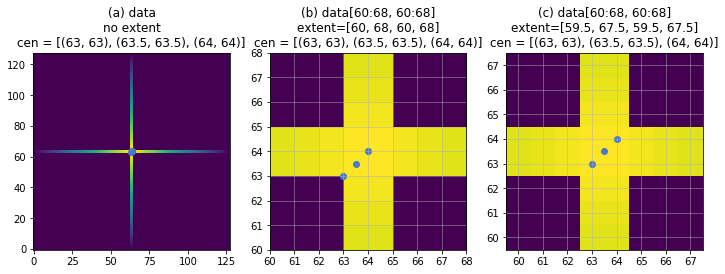
重心位置の確認などをするために上図2のようにextentを指定して拡大すると、imshowのインデックスベースでプロットしたつもりの点が縦横座標ともに0.5ずれて表示されてしまいます。これはもっと大きなデータを扱っている時に勘違いの原因になります。先に定義したdata128を使って見てみます。
fig, axes = plt.subplots(1, 3, figsize=(12,4))
axes[0].imshow(data128, origin='lower')
axes[1].imshow(data128[60:68, 60:68], origin='lower', extent=[60, 68, 60, 68])
axes[2].imshow(data128[60:68, 60:68], origin='lower', extent=[59.5, 67.5, 59.5, 67.5])
titles = ['(a) data\nno extent\ncen = {}',
'(b) data[60:68, 60:68]\nextent=[60, 68, 60, 68]\ncen = {}',
'(c) data[60:68, 60:68]\nextent=[59.5, 67.5, 59.5, 67.5]\ncen = {}']
for ax, title in zip(axes, titles):
if not '(a)' in title:
ax.xaxis.set_major_locator(MultipleLocator(1))
ax.yaxis.set_major_locator(MultipleLocator(1))
ax.grid(True, alpha=0.6)
ax.set_title(title.format(cen128))
ax.scatter(np.array(cen128)[:, 0], np.array(cen128)[:, 1])
十字テストデータの中心部分をprintして確認した通り、data128のインデックスベースの重心座標は[63.5, 63.5]です。ところが拡大につかったインデックスと同じ値をextentに設定してしまうよくある間違いをしている上図(b)では[64, 64]が中心であるかに見えてしまいます。拡大をしていない(a)では中心付近に点を打っても正確な位置は当然わからないので、実際の測定データを扱っていると上図(b)がおかしいことにはなかなか気づきません。
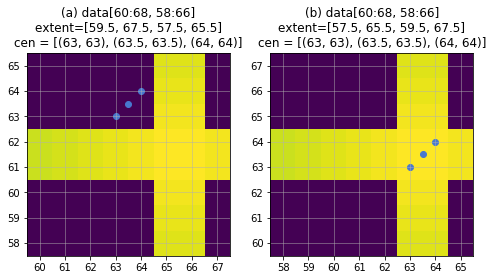
拡大範囲とextentの順番に注意
上の例では横軸縦軸ともにおなじインデックス範囲を拡大しているのでextentの数字の並び順を気にする必要はありませんでしたが、extentの指定でも前述したインデックスベースの座標[i,j]と慣習的なxy座標での(x,y)の混同が起きやすいです。
# iminからimax-1、jminからjmax-1までの範囲を拡大したい場合
# 間違い
plt.imshow(data[imin:imax, jmin:jmax], extent=[imin-0.5, imax-0.5, jmin-0.5, jmax-0.5])
# 正しい
plt.imshow(data[imin:imax, jmin:jmax], extent=[jmin-0.5, jmax-0.5, imin-0.5, imax-0.5])
# data128による具体例
fig, axes = plt.subplots(1, 2, figsize=(8,4))
axes[0].imshow(data128[60:68, 58:66], origin='lower', extent=[59.5, 67.5, 57.5, 65.5])
axes[1].imshow(data128[60:68, 58:66], origin='lower', extent=[57.5, 65.5, 59.5, 67.5])
titles = ['(a) data[60:68, 58:66]\nextent=[59.5, 67.5, 57.5, 65.5]\ncen = {}',
'(b) data[60:68, 58:66]\nextent=[57.5, 65.5, 59.5, 67.5]\ncen = {}']
for ax, title in zip(axes, titles):
ax.xaxis.set_major_locator(MultipleLocator(1))
ax.yaxis.set_major_locator(MultipleLocator(1))
ax.grid(True, alpha=0.6)
ax.set_title(title.format(cen128))
ax.scatter(np.array(cen128)[:, 0], np.array(cen128)[:, 1])
上の図では中心部にあるはずの三点の位置が違うので何かおかしいとすぐに気づきますが、軸の値をきちんと確認しないと見過ごしやすい間違いです。
extentを使ったピクセル座標から物理量への変換
extentはピクセル座標がピクセル中心にくるように拡大表示するときだけでなく、縦軸横軸の数字を0始まり整数のピクセル座標から物理量に変換するためにも使えます3。ただし、ここでもextentの指定の仕方に注意が必要です。
# ピクセルの位置をはっきりさせるため10x10の乱数を作る
data10_rand = np.random.rand(10, 10)
# 各ピクセルの位置と対応する仮の物理量。二次元検出器の場合は角度や散乱ベクトルの値を使う。
x = np.linspace(-0.3, 0.5, 10)
y = np.linspace(-0.2, 0.6, 10)
dx = x[1]-x[0] # ピクセル間の差分
dy = y[1]-y[0] # dxと同じ値だが明示的に計算しておく
print('x:', x)
print('y:', y)
fig, axes = plt.subplots(1, 4, figsize=(16,4))
fig.subplots_adjust(wspace=0.3)
axes[0].imshow(data10_rand, origin='lower')
extent = [min(x), max(x), min(y), max(y)]
axes[1].imshow(data10_rand, origin='lower', extent=extent)
extent = [min(x)-dx/2, max(x)+dx/2, min(y)-dy/2, max(y)+dy/2]
axes[2].imshow(data10_rand, origin='lower', extent=extent)
axes[3].imshow(data10_rand, origin='lower', extent=extent)
titles = ['(a) data10\nno extent',
'(b) data10\n[min(x), max(x), min(y), max(y)]',
'(c) data10\n[min(x)-dx/2, max(x)+dx/2,\n min(y)-dy/2, max(y)+dy/2]',
'(d) data10\n[min(x)-dx/2, max(x)+dx/2,\n min(y)-dy/2, max(y)+dy/2]']
for ax, title in zip(axes, titles):
ax.set_title(title, y=1.04)
ax.grid(True, which='both', alpha=0.6)
if '(a)' in title:
ax.xaxis.set_major_locator(MultipleLocator(1))
ax.yaxis.set_major_locator(MultipleLocator(1))
else:
ax.set(xticks=x[::2], yticks=y[::2])
ax.xaxis.set_major_formatter(StrMethodFormatter('{x:.3f}'))
ax.xaxis.set_minor_locator(AutoMinorLocator(2))
ax.yaxis.set_major_formatter(StrMethodFormatter('{x:.3f}'))
ax.yaxis.set_minor_locator(AutoMinorLocator(2))
# extentを使うと拡大表示にxとyの値がそのまま使える
if '(d)' in title:
ax.set(xlim=(-0.1, 0.3), ylim=(-0.05, 0.35))
x: [-0.3 -0.21111111 -0.12222222 -0.03333333 0.05555556 0.14444444
0.23333333 0.32222222 0.41111111 0.5 ]
y: [-0.2 -0.11111111 -0.02222222 0.06666667 0.15555556 0.24444444
0.33333333 0.42222222 0.51111111 0.6 ]
extentを指定していない(a)ではこれまで説明した通り0始まり整数のピクセル座標を示すtick(目盛り)が各ピクセルの中心を表すように配置されています。(b)ではextentをつかって物理量(ここではサンプルコード中のxとy)に変換できているように見えますが、実はこれはよくありがちな間違ったextentの使い方の例です。グリッドの交点を見ると、ピクセル位置に対応しているつもりで設定したtickがピクセルの中心を通っていないことがわかります。一方、extentを正しく使っている(c)では意図した通りにピクセル中央にピクセル位置と対応したxとyの値を示すtickが配置されています。extent=[left, right, bottom, top]が__左右上下端のピクセルの座標ではなく表示領域の左右上下端の数字を指定するオプション__であることを考えるとこの違いは当然なのですが、実際のデータは上で使った乱数のようにピクセルの区別がつきやすい見た目をしているわけではなく、さらにわざわざピクセル位置にtickを置いたりグリッドを表示したりしないためなかなか間違いに気づきません4。
ピクセル座標を物理量に変換するという目的を達成するには、実は「座標スケールは0始まり整数のままでFuncFormatterを使って表示する数字(tick label)だけを無理やり物理量を表す数字にしてしまう」という方法も使えます。ただし、この方法では軸のスケール自体は0始まり整数のままなのでax.set_xlimやデータのslicingを使って拡大表示したい時に常に整数のピクセル座標を使う必要が生じます。実際の作業を想像すればこれがあまり便利でないことはわかるでしょう。x軸の物理量が0.1から0.25に相当する部分を拡大するには何番目のピクセルを指定したらいいか調べないといけない方法を好む人なら別ですが。(d)に示した通りextentを正しく指定すれば、拡大表示にxやyの物理量をそのまま指定できます。
pyFAIで一次元化する際も座標の定義に注意
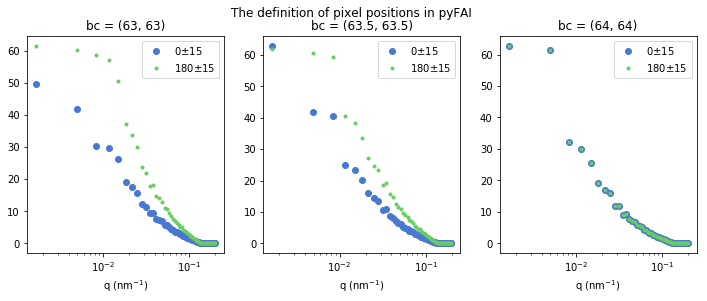
二次元検出器の測定データの解析では、ある方向の強度のみを切り出す一次元化という処理を行うことが多いです。この際、ビームセンターと呼ばれる強度による重み付き重心を原点とした極座標を設定して一次元化を行います。pyFAIでは、これまで述べてきたピクセル中央を基準にした座標ではなくピクセル左下を基準にした座標を使っているので、2D arrayのインデックスベースで算出したビームセンターの値をそのままpyFAIに渡すと誤った結果になってしまいます。これは下の例のように、2D arrayのインデックスベースの重心([63.5, 63.5])に0.5を足した値([64, 64])をpyFAIに渡すことで解決します。
# 一次元化に使うパラメータの例
pixel, wv, dist = 0.0075, 1.2, 18 # in m, nm, m
# 一次元化する方向と角度の範囲
az, daz = 0, 15
# 一次元化に必要なパラメータの設定
ai = pyFAI.AzimuthalIntegrator(dist=dist, pixel1=pixel, pixel2=pixel, wavelength=wv*1e-9)
# 動径方向、角度方向のbinning個数
rbin, azbin = 60, 360
fig, ax = plt.subplots(1, 3, figsize=(12, 4))
fig.suptitle('The definition of pixel positions in pyFAI')
for i, bc in enumerate(cen128):
ai.setFit2D(dist*1000, *bc) # distance in milimeter
q, I = ai.integrate1d(data128, rbin, azimuth_range=(az-daz, az+daz))
q1, I1 = ai.integrate1d(data128, rbin, azimuth_range=(az+180-daz, az+180+daz))
ax[i].set_title('bc set to '+str(bc))
ax[i].set_xscale('log')
ax[i].set_xlabel('q (nm$^{-1}$)')
ax[i].tick_params(axis='x', which='minor')
ax[i].plot(q, I, 'o', label=str(az)+'$\pm$'+str(daz))
ax[i].plot(q1, I1, '.', label=str(az+180)+'$\pm$'+str(daz))
ax[i].legend()
ここでは以下の図の二つの白い部分の強度をそれぞれの範囲の中で合計して動径の関数としてプロットしています。pyFAIに正しいビームセンターが設定されている場合は左右の白い部分は同じ強度を持つはずなので二つのプロットは一致するはずで、確かに[64, 64]のときに一致しているのがわかります。

data128をimshowで拡大した図を使って説明すると
- 2D arrayのインデックスベースの座標で計算した重心
[63.5, 63.5]はcで正しい位置に表示される -
pyFAIはbのようにピクセル左下を基準にした座標で採用しているので、2D arrayインデックスベース座標の重心[63.5, 63.5]を0.5ずつずらした[64, 64]が重心になる
とも言えます。
-
実際に間違ってみない限り、このように言葉で説明されてもピンとこないと思いますが、一度読んでおくと何かおかしいことに気づいた時の解決の助けになると思います。 ↩
-
転置をしてから[0,0]が左下にくるように表示すれば転置前のdata[i,j]が(x,y)座標表記で(i,j)にくるようにはできますが、転置をする方式を採用すると、転置を忘れた際に何が何だか分からなくなるので私はあまりオススメしません。 ↩
-
imshowは画像データのように等間隔に並んだ数字の可視化に使います。したがって、ここで縦軸と横軸に割り当てる物理量はピクセル座標と線形関係にあるものを想定しています。 ↩ -
実際のデータは最低でも128x128ピクセルはあるでしょうから、データ全体を表示している時は気づかない程度の差しかないとも言えますが、
ax.set_xlimなどで拡大すると意図した領域から少しずれた部分を拡大することになります。 ↩