Go to Qiita Advent Calendar 2024 Top
LoginSignup
28
27

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

@skotaro(斉藤 耕太郎)

matplotlibを使って二次元検出器の二次元強度マップを作る

Last updated at Posted at 2017-12-11

「実験屋のためのPython」初回によせて

大型実験施設のみならず実験室でも測定条件空間を密に埋める大量の測定データを取得できるようになってきました。 エクセルは言わずもがな、GUIベースのグラフ作成ソフトで頑張ることに限界を感じ始めてる方も多いのではないでしょうか1。GUIとCUIの良し悪しや好き嫌いについての意見はいろいろありますが、本稿でも使っているJupyter Notebookは両者のいいとこ取りをしたおそらくデータ解析における革命的なツールです。私は二次元検出器を使った実験のデータ解析とグラフ作成をほぼ完全にPython+Jupyterに切り替えましたが、matplotlibの細かい調整のしにくさ以外に困っていることはありません2。テキストエディタを使ってFortran/Cとシェルスクリプトとsed/awkとgnuplotでゴリゴリやっていくスタイル以外に、再現性を確保しやすいスクリプトベースの解析手法の選択肢ができたのは研究者にとって嬉しい出来事だと思います。重い数値計算が含まれない限り、便利なパッケージが充実しているPythonを使えば実験屋が必要とするほとんどの解析関連タスクは（あなたの想像以上に）簡単に実現できるでしょう3。また、所属組織の事情によりエクセル以外の数値処理向け有料ソフトを買えないという方にとっては、無料のPython+Jupyterは（時間的な学習コストさえ払えれば）とても頼れる道具になると思います。この記事がそういった方の役に立ってくれれば嬉しいです。

「実験屋のためのPython」と大きく出ましたが、私が普段扱っている二次元データ解析にまつわるあれこれについて掲載予定です。シリーズ化しておすそ分けできるほどのノウハウのストックもないので、ひとまず構想があるのは五、六回分のみです。諸々のインストールやPythonの基礎、matplotlib.pyplotを使ったグラフ作成の基本には触れず、ある程度具体的なタスクの手順と注意点を述べる逆引きっぽい記事を、日本語情報が少ない場合はもう少し粒度の細かい「〜する方法」のような記事を書いていきます。

今回の内容

データの読み込みと二次元強度マップの表示という最もよくあるタスクについて書きます。もう少し具体的に述べると以下になります。

  • 二次元検出器で測定したデータをnumpy.ndarrayとして読み込む（CSVとHDF5の場合について説明）
  • imshowを使って二次元強度分布マップを作る

小角散乱や粉末回折実験の場合に必要となる一次元化データを作成する方法は後日公開します。

必要な環境とパッケージ

  • conda
  • Python 3.6
  • Jupyter notebook
  • numpy, matplotlib, h5py

h5pyはconda-forgeチャンネルからインストールできます。

conda install -c conda-forge h5py

notebookの一番上のセルでパッケージをまとめてimportするのがいいと思います。

%matplotlib inline # データ解析する際に便利なjupyter notebookのmagic word
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-muted')
import h5py

matplotlibのスタイルは公式ドキュメントのこのページや網羅はされていませんがこのギャラリーを参照して好きなものを選ぶとよいでしょう。

測定データの読み込み

HDF5の場合

測定装置の吐くHDF5ファイルにはたいてい測定データと解析や整理に必要な各種測定パラメータがその装置特有のディレクトリ構造で記録されているはずです。まずは読み込みたい情報(object)がHDF5ファイル内のどこに格納されているか把握しなければなりません。HDFViewで一つずつポチポチ探していくのもいいのですが、せっかくなのでh5pyパッケージのGroupクラスのvisit(callable)メソッドを使ってファイル内に格納されている全objectのリストを表示してみます。

visit(callable)は_callable_がNoneを返す限り再帰的にHDF5ファイル内の全てのobjectを訪れて_callable_を実行してくれます。つまり、どんなobjectに対してもその場所を表示してNoneを返す_callable_を作れば全objectのリストが得られます。以下のfind_groupはマニュアルの例を少し書き換えたものです。

def find_group(name):
    if '' in name: # = for any objects in a HDF file,
        print(name) # print the path to a object.
        return None # returning None to visit all objects recursively.

path = 'hdf/yourdata.hdf'
with h5py.File(path,'r') as f:
    f.visit(find_group)

以下は私の手元にあるHDF5ファイルに対して上記コードを実行した結果の一部です。上から三つがディレクトリでそれ以降は測定パラメータであろうことがわかります。

entry1
entry1/SANS
entry1/SANS/Dornier-VS
entry1/SANS/Dornier-VS/lambda
entry1/SANS/Dornier-VS/rotation_speed
entry1/SANS/Dornier-VS/tilt_angle
entry1/SANS/Dornier-VS/type
...
...

欲しいobjectの目星がついたらHDFViewで確認するとよいでしょう。あとは必要なobjectを読み込む関数を作るだけです。以下は私が使っている関数の例です。測定データをfloat型の2次元numpy.ndarrayとして、測定環境によらず記録されているはずの測定条件をdictionaryにまとめてreturnしています。

def ReadDataAndHeaderFromHDF(hdfpath):
    with h5py.File(hdfpath, 'r') as f:
        data = f['entry1/SANS/detector/counts'][()].astype('float')
        time = f['entry1/SANS/detector/counting_time'][0]
        mon1 = f['entry1/SANS/monitor1/counts'][0]
        mon2 = f['entry1/SANS/monitor2/counts'][0]
        name = f['entry1/sample/name'][0].decode('utf-8') # 文字列データをエンコード
        wv = f['entry1/SANS/Dornier-VS/lambda'][0]
        SD = f['entry1/SANS/detector/x_position'][0]

    return data, {'time':time, 'mon1':mon1, 'mon2':mon2, 'mon1d':mon1d, 'mon2d':mon2d, 'name':name, 'wv':wv, 'SD':SD}

path = 'hdf/yourdata.hdf'
data, header = ReadDataAndHeaderFromHDF(path)

パスの後ろの[()]と[0]はそれぞれnumpy.ndarrayのviewと要素が一つのlistに格納された数値を取得するためにつけています。あなたの持っているHDFファイルの読み込みでこれらが必要かはわかりません。以下のようなコードを実行するとどうしたらいいかわかると思います。

with h5py.File(path, 'r') as f:
    print(type(f['path/to/scalar_value']))
    print(f['path/to/scalar_value'])
    print(f['path/to/scalar_value'][:])
    print(f['path/to/scalar_value'][0])
    print(type(f['path/to/2d_array']))
    print(f['path/to/2d_array'])
    print(type(f['path/to/2d_array'][()]))
    print(f['path/to/2d_array'][()])

CSVの場合

ここでは、二次元検出器が記録した各ピクセルの強度情報が見た目そのままの行列としてCSVファイルに保存されている以下のようなCSVファイルを考えます。冒頭数行は測定条件などのヘッダ情報です。

# measurement conditions
# motor1=100
# motor2=10
# temperature=30
0.,  0.,  2.,  0.,  0.,  0.,  0.,  0.,  0.,  0.
1.,  1.,  2.,  1.,  1.,  1.,  1.,  1.,  1.,  1.
0.,  0.,  2.,  0.,  0.,  0.,  0.,  0.,  0.,  0.
0.,  0.,  2.,  0.,  0.,  0.,  0.,  0.,  0.,  0.
0.,  0.,  2.,  0.,  0.,  0.,  0.,  0.,  0.,  0.
0.,  0.,  2.,  0.,  0.,  0.,  0.,  0.,  0.,  0.
0.,  0.,  2.,  0.,  0.,  0.,  0.,  0.,  0.,  0.
0.,  0.,  2.,  0.,  0.,  0.,  0.,  0.,  0.,  0.
0.,  0.,  2.,  0.,  0.,  0.,  3.,  0.,  0.,  0.
0.,  0.,  2.,  0.,  0.,  0.,  0.,  0.,  0.,  0.

文字列をうまく処理すればヘッダ情報の読み込みもできますが、この部分は各装置のフォーマットに強く依存するのでここでは強度情報のみを対象とします4。読み込みにはnumpy.genfromtxtを使います。

path = ./csv/yourdata.csv
data = np.genfromtxt(path, delimiter=',', skip_header=4)

上の例で使っているdelimiterとskip_headerのほかは、skip_footerとdtypeあたりの利用頻度が高いと思います。詳しくはマニュアル [numpy.genfromtxt] (https://docs.scipy.org/doc/numpy/reference/generated/numpy.genfromtxt.html) を参照してください。

二次元強度分布マップの表示

HDFデータの場合のみを書きます。CSVファイルやその他の形式の場合はデータの読み込み部分が異なるだけで可視化部分はそのまま適用できます。

測定データを一つずつ表示してPNGとして保存

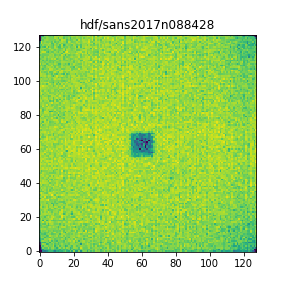
以下は、小角散乱の二次元強度分布にnp.log10を適用して表示する際の例です。np.log10の警告を避けるために、強度0のピクセルにあらかじめNaNを代入するSafeLog10という関数を定義して使っています。LoadHDFAndPlotは測定の現場ですぐに結果を確認する際に便利な関数です。また測定データのみを読み込むReadDataFromHDFを使っています。fig.savefigのコメントを外せば強度分布をpngファイルに保存します。

def ReadDataFromHDF(hdfpath):
    with h5py.File(hdfpath,'r') as f:
        data = f['entry1/SANS/detector/counts'][()].astype('float')
        
    return data

def SafeLog10(data, nansub=None):
    tmp = np.copy(data) # tmp = data としてtmpを変更すると元データdataを変更されてしまう（はず）
    tmp[np.where(tmp <= 0)] = np.nan # np.log10のRuntimeErrorを避けるために0にnanを代入
    log = np.log10(tmp)
    if nansub is not None:　# tmpのnanに対してnp.log10が返したnanを他の値に変える
        log[np.isnan(log)] = nansub 
    return log

def LoadHDFAndPlot(hdfpath):
    filename = os.path.splitext(hdfpath)[0] # パスが長い場合に備えて自明な拡張子を除去
    data = SafeLog10(ReadDataFromHDF(hdfpath), nansub=0)
    fig = plt.figure(figsize=(4,4)) # 正方形のFigureオブジェクトを作成
    ax = fig.gca() # figのAxesオブジェクトを取得 gcaは'get current axis'
    ax.set_title(filename) # axにタイトルを設定する
    ax.imshow(data, origin='lower') # axにimshowで二次元プロットを画像として描画する
#    fig.savefig('{}.png'.format(filename.split('/')[1]))

path = 'hdf/sans2017n088428.hdf'
LoadHDFAndPlot(path)

sans2017n088428.png

描画部分にコメントで少し説明を書きましたが、FigureやAxesについては [matplotlibの階層構造を知ると幸せになれる(かもしれない) - Qiita] (https://qiita.com/ceptree/items/5fb5e9e6f29d214153c9) が参考になります。タイトルや軸のラベルなどの設定はいろいろな流儀がありますが、この階層構造について理解しているとスッキリします。

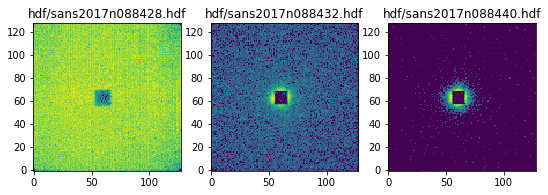
複数のデータを一つのfigにまとめて表示

hdfフォルダに入っているHDFファイルを名前順にソートしたリストの中から、最初の三つだけを選んで一つのfigに表示します。

import glob

hdfpaths = sorted(glob.glob('hdf/*.hdf'))
num = 3
fig, axes = plt.subplots(1, 3, figsize=(n*3,3))
for ax, path in zip(axes, hdfpaths[:n]):
    data = SafeLog10(ReadDataFromHDF(path), nansub=0)
    ax.set_title(path)
    ax.imshow(data, origin='lower', aspect='equal')

download.png

上の例ではimshowのvmin、vmaxオプションを指定していないので各データの最小値、最大値で色のスケールが決まっていますが、温度依存測定などでは全てのデータで共通の値に指定すれば色のスケールを揃えることができます。

見た目などの細々とした調整

いろいろあってキリがないのでここではすべて触れません。よく使われる見た目の調整はQiitaのmatplotlibタグの中から探すだけでも解説が見つかると思います。ただ、適切な大きさのカラーバーをつけるといったよくある操作さえややこしいことをする必要があったり、少し凝ったことになるとドンピシャの説明にたどり着くのが急に難しくなってしまうのがmatplotlibの困ったところです。オブジェクト指向の考え方とmatplotlibの設計思想を理解していないと、正しいキーワードを使った検索ができずに「近いところまでいくけど最後の一歩がわからない」という状況に陥ると思います。私の場合は、主にStack Overflowの回答と公式マニュアルをつまみ読みしながらなんとなく理解した気になっています。やりたいことだけをつまみ食いしていると必ず細かい調整でつまずくので、英語が読めるならver. 2.1から改善された公式チュートリアルを一読するのをすすめます。なかでも特に重要な基礎知識であるArtistについては以下の解説を参考にしてください。
早く知っておきたかったmatplotlibの基礎知識、あるいは見た目の調整が捗るArtistの話 - Qiita

複数桁にまたがるデータをlogスケールで表示する

見た目の調整に関してlogスケールのの扱いについて少し述べておきます。例えば小角散乱実験で得られる強度分布では、ピークがぴょこぴょこと見える通常の回折実験とは異なり、中心近傍の非常に強い値から検出器の外側に向かって強度が指数関数で減少します。このようなデータを可視化するにはlogスケールが適しており、このとき0カウントのピクセルやバックグラウンドを差し引いた際の負の値を持つピクセルの扱いが気になります。これまで示した例ではSafeLog10関数を使って0と負の値のlogを0やNaNに置き換えてimshowで表示していましたが、実はimshowのnormキーワードを使うとlogにする前のデータに同様の処理を施してlogスケールで色付けしてくれます。

from matplotlib.colors import LogNorm

data = ReadDataFromHDF(path)
ax.set_title(path)
ax.imshow(data, origin='lower', aspect='equal', norm=LogNorm())

LogNormの効果やlogスケールのcolorbarについての詳細は以下を参照してください。
matplotlibのcolorbarを解剖してわかったこと、あるいはもうcolorbar調整に苦労したくない人に捧げる話 > tick関連調整の例：桁の異なる数値を持つ二次元データをlogスケールで色付けし、colorbarに適切なtickをつける

imshowかpcolormeshか

matplotlib.pyplotにはピクセルベースの強度分布表示に使えそうなimshowとpcolormeshという二つの関数があります。[このnotebook]
(http://nbviewer.jupyter.org/gist/mkatsura/6052047)で比較してる通り、オプションを駆使すればどちらを使ってもほぼ同じ絵をかけます。`pcolormesh`の強みはnonuniformなデータの描画が可能な点ですが、`imshow`はuniformなデータしか描画できない代わりに`pcolormesh`より速いです。二次元検出器で測定したデータはピクセルごとに記録されている等間隔のuniformなデータなので`imshow`のほうがよいでしょう[^5]。以下に示すのは前述のnotebookのコードを少し改変した四種類の二次元プロット関数の見た目と実行時間の比較です。`pcolormesh`より`imshow`のほうが3倍速いのがわかります。外場依存性測定などの大量のデータを表示する際にこの差は非常に大きいです。

import time

def lorentz(x, y, x0, y0, width, height):
    return height/(1+((x-x0)/width)**2+((y-y0)/width)**2)

size = (15, 20)
npeak = 50
# ランダムな場所にランダムな高さのローレンツ関数をnpeak個作る
v0 = np.random.randint(size[0]+1, size=npeak)
h0 = np.random.randint(size[1]+1, size=npeak)
height = np.random.random(npeak)*size[1]*0.1

H, V = np.meshgrid(range(size[1]), range(size[0]))
M = np.empty((*size, npeak))

for i, (h0_, v0_, z0) in enumerate(zip(h0, v0, height)):
    # lorentz関数のwidthにz0を流用
    M[:,:,i] = lorentz(H.ravel(), V.ravel(), h0_, v0_, z0, z0).reshape(size)
    
M = M.sum(axis=2)

fig, ax = plt.subplots(1,4, figsize=(20,6))

ax[0].set_title('imshow')
start = time.time()
ax[0].imshow(M, origin='lower', interpolation='none')
print('imshow: \t{:.5f}s'.format(time.time()-start))
ax[1].set_title('pcolormesh')
start = time.time()
ax[1].pcolormesh(M)
ax[1].set_aspect('equal')
print('pcolormesh:\t{:.5f}s'.format(time.time()-start))
ax[2].set_title('contouf')
start = time.time()
ax[2].contourf(M)
ax[2].set_aspect('equal')
print('contourf:\t{:.5f}s'.format(time.time()-start))
ax[3].set_title('contour')
start = time.time()
ax[3].contour(M)
ax[3].set_aspect('equal')
print('contour:\t{:.5f}s'.format(time.time()-start))

imshow: 	0.00054s
pcolormesh:	0.00141s
contourf:	0.00515s
contour:	0.00854s

download-1.png

カラーマップについて

二次元プロットのカラーマップは長らくjetやrainbowとよばれるカラフルなものが好まれてきましたが、[How Bad Is Your Colormap?]
(https://jakevdp.github.io/blog/2014/10/16/how-bad-is-your-colormap/) や [matplotlibのマニュアル] (http://matplotlib.org/users/colormaps.html) に述べられている通り、これらはデータ本来の様子を認知的に歪める作用があります。これらに代わりここ数年で論文でも使われるようになってきたのがperceptually uniform sequentialなカラーマップです。matplotlib 2.0ではデフォルトのカラーマップがそれまでのカラフルなjetから、[perceptually uniform sequentialなviridisに変更] (https://matplotlib.org/users/dflt_style_changes.html#colormap)されました。他にも数種類あるので[公式サイトのカラーマップ見本](https://matplotlib.org/tutorials/colors/colormaps.html)のperceptually uniformな四つから好きなものを選ぶのが良いでしょう。

  1. 例えば、私が以前使っていたIgor Proは、データ解析途中の結果をある程度の処理ごとに保存することを促す設計思想であるため、二次元データの温度依存性測定などの解析をしているとファイルサイズがあっというまに数百MBに達してしまい非常に扱いづらく感じることがしばしばありました。 ↩

  2. 逆に言うとmatplotlibの細かい調整のしにくさがボトルネックです。 ↩

  3. Python + Jupyter notebookの再現性の高さと想像以上の簡単さの現時点での最たる例は[LIGOが公開している重力波解析チュートリアル] (https://losc.ligo.org/s/events/GW150914/LOSC_Event_tutorial_GW150914.html)でしょう。 ↩

  4. 測定条件の読み込みは装置ごとのフォーマットに合わせた文字列処理の必要ないHDF5形式がとても楽です。 ↩

28
27
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
28
27

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?