この記事について
マウスだけ!で作る量子テレポーテーションで扱った量子テレポーテーションは、古典ビットを使って量子状態を転送しました。
この逆操作である、超高密度符号化実験(Superdense coding)について扱っていきたいと思います。
上記記事と同様に、
- 前半は、量子シミュレータをマウスで操作することで、量子回路を構成し
- 後半は、数式を用いて超高密度符号化実験の操作を追っていきます
一応、前半のマウス操作だけで理解できる構成にした(つもり)ですが、興味が湧いた方は、
後半の数式も参照頂ければと思います。
なお、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
また、実際にAmazon Braketを利用し動きを見たい方は、下記を参照ください。
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}
量子テレポーテーションとの比較
超高密度符号化実験と量子テレポーテーションを下記に比較します。
下記のように、「送信したいもの」と「利用する道具」が逆転していることがわかります。
| 送信したいもの | 利用する道具 | |
|---|---|---|
| 量子テレポーテーション | 1量子状態 | 古典2ビット |
| 超高密度符号化実験 | 古典2ビット | 1量子状態 |
超高密度符号化実験の回路
非常にシンプルです。下記のリンクをクリックすることで、Quirkで回路を開くことができます。

では、回路を詳細に見ていきましょう。
| # | 回路 | 説明 |
|---|---|---|
| 1 |  |
量子テレポーテーションの記事で見たとおり、2量子のもつれあい(相互作用)を発生するBell回路で、H+CNOTで構成されます。 |
| 2 |  |
送信者が、操作することができる量子ゲートです。 図はXゲート(NOT)ですが、量子テレポーテーションと同様に送信したいメッセージ(古典2ビット)に対応して、利用するゲートを選択します。 ゲートをどう選択するか?は後述します |
| 3 |  |
量子テレポーテーションの記事で見たとおり、2量子のもつれあい(相互作用)を解消し、Bell測定を行うための逆Bell回路です。Bell回路と逆の構造をしています。 |
送信者のゲートの選択
送信者は、送信したいメッセージの古典2ビット(00/01/10/11)に応じ、ゲートを選択し適用することで、量子1ビットに対する操作で、古典2ビットのメッセージを送信します。
ゲートの選択は下記の通りです。
| # | 送信 MSG |
適用 ゲート |
結果 |
|---|---|---|---|
| 1 | $00$ | ※なし |  |
| 2 | $01$ | $X$ |  |
| 3 | $10$ | $Z$ |  |
| 4 | $11$ | $XZ$ | 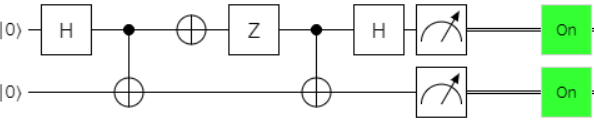 |
実際に、Quirk上で送信者が操作するゲートを入れ替えていただけるとわかりやすいと思います
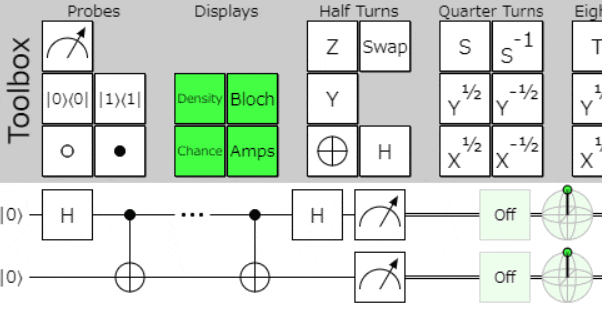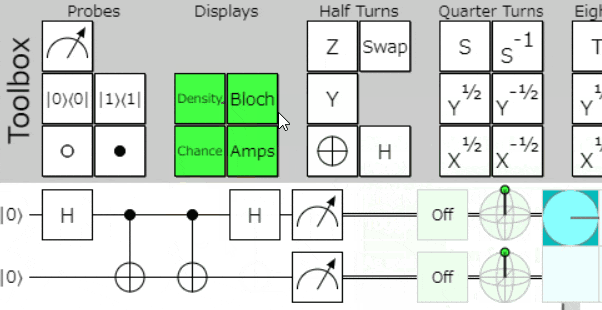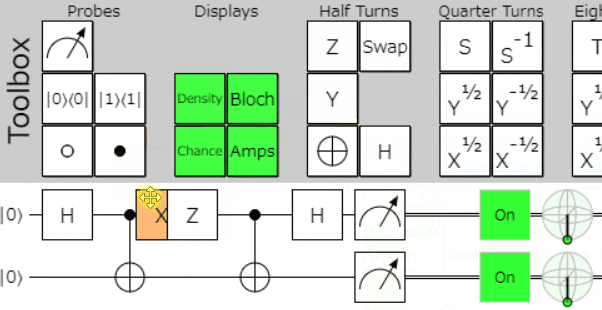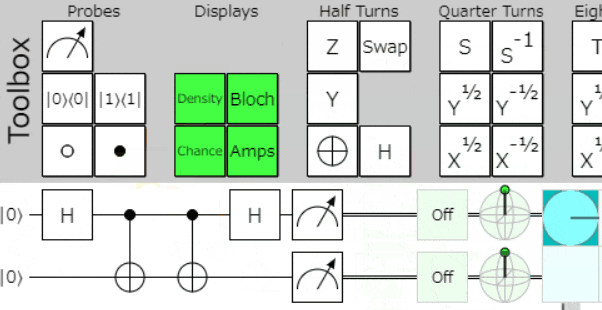
ちょっとおしゃれにする(余談)
送信に利用するゲート選択を、時々刻々と変化させるようにするとこんな感じになります。
送信者の送信メッセージが、受信者に同じビットパターン(00,01,10,11)で伝わるのがわかりやすいかと思います。

ここまでのまとめ
量子テレポーテーションの逆操作である、超高密度符号化実験(Superdense coding)について扱いました。このアルゴリズム(操作)が何ができる?というわけではないのですが、両者ともに共通して言えるのは、
- Bell回路にて発生させた量子のもつれあいが重要な要素である
- もつれあいを利用することで「量子1ビット→古典2ビット、古典2ビット→量子1ビット」を行き来することができる。
という面白い特性を持ちます。
実用的なアルゴリズムをこれから勉強する際に、量子の「重ね合わせ」や「もつれあい」に慣れ親しむ意味でも、これらに触れることは良い経験であると考えています。
最後に数式で確認
上記で概要は把握頂けたかと思いますが一応最後に、数式で確認していきたいと思います
なお、量子ゲートの$braket$での演算に慣れていない方は先に、下記を参照ください。
00)ゲート操作無し

まずは、Bell回路で「もつれあい」を作ります
\displaylines{
\ket{00}
\xrightarrow[]{H_{1}}
\frac{1}{\sqrt{2}}(\ket{0}+\ket{1}) \otimes\ket{0}
\\
=\frac{1}{\sqrt{2}}(\ket{00}+\ket{10})
\
\xrightarrow[]{CX_{12}}
\
\frac{1}{\sqrt{2}}(\ket{00}+\ket{1\color{redk}{1}})
}
そしてゲート適用をせずに、逆Bell回路に掛けます
\displaylines{
\frac{1}{\sqrt{2}}(\ket{00}+\ket{11}
\xrightarrow[]{CX_{12}}
\frac{1}{\sqrt{2}}(\ket{00}+\ket{1\color{red}{0}})
\\
\xrightarrow[]{H_{1}}
\frac{1}{\sqrt{2}}\left(\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes\ket{0}+\frac{1}{\sqrt{2}}(\ket{0}-\ket{1})\otimes\ket{0}\right)
\\
=\frac{1}{2}\left(\color{blue}{\ket{00} + \ket{10} }\color{blue}{+ \ket{00}} \color{red}{- \ket{10}}\right)
}
ここで、赤と青の項に注目すると、
- $\ket{00}$は両方とも$\color{blue}{+}$であり、相互に強め合う関係
- $\ket{10}$は一方が$\color{blue}{+}$、一方が$\color{red}{-}$であり、弱め合う関係
波の干渉を思い出していただくとわかるのですが、波が強めあい、弱め合う、干渉により波動の状態が収縮します。
そして、
\frac{1}{2}\left(\color{blue}{\ket{00} + \ket{10} }\color{blue}{+ \ket{00}} \color{red}{- \ket{10}}\right) = \frac{1}{2}(2 \times \ket{00}) = \ket{00}
となります。$\ket{00} = \ket{0} \otimes \ket{0}$であり、係数は$1^2=1$ということで、両ビットとも100%で0が観測できます。つまり、受信者は古典2ビット(00)を得ます。
では、残りも見ていきましょう。
01)Xゲート適用

Bell回路でもつれあいを作るところまでは一緒で、${X_1}$ゲートを適用します。
\ket{00}
\xrightarrow[]{H_{1} CX_{12}}
\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})
\xrightarrow[]{X_1}
\frac{1}{\sqrt{2}}(\ket{\color{red}{1}0}+\ket{\color{red}{0}1})
これの状態に逆Bell回路を適用すると
\displaylines{
\frac{1}{\sqrt{2}}(\ket{10}+\ket{01})
\xrightarrow[]{CX_{12}}
\frac{1}{\sqrt{2}}(\ket{1\color{red}{1}}+\ket{01})
\\
\xrightarrow[]{H_{1}}
\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{01}-\ket{11}+\ket{01}+\ket{11})
\\
=\frac{1}{\sqrt{2}}(2 \times \ket{01}) = \ket{01}
}
上述と同様に、干渉による強めあい、弱めあいで、$\ket{01}$が残ります
10)Zゲート適用

Bell回路でもつれあいを作るところまでは一緒で、${Z_1}$ゲートを適用します。
\ket{00}
\xrightarrow[]{H_{1} CX_{12}}
\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})
\xrightarrow[]{Z_1}
\frac{1}{\sqrt{2}}(\ket{00}\color{red}{-}\ket{\color{red}{1}1})
これの状態に逆Bell回路を適用すると
\displaylines{
\frac{1}{\sqrt{2}}(\ket{00}-\ket{11})
\xrightarrow[]{CX_{12}}
\frac{1}{\sqrt{2}}(\ket{00}-\ket{1\color{red}{0}})
\\
\xrightarrow[]{H_{1}}
\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{00}+\ket{10}-\ket{00}+\ket{10})
\\
=\frac{1}{\sqrt{2}}(2 \times \ket{10}) = \ket{10}
}
同様に波動の干渉で、$\ket{10}$が残ります。
11)XZゲート適用

最後です。Bell回路でもつれあいを作るところまでは一緒で、$X_1Z_1$ゲートを適用します。
\displaylines{
\ket{00}
\xrightarrow[]{H_{1} CX_{12}}
\frac{1}{\sqrt{2}}(\ket{00}+\ket{11})
\\
\xrightarrow[]{X_1}
\frac{1}{\sqrt{2}}(\ket{\color{red}{1}0}+\ket{\color{red}{0}1})
\xrightarrow[]{Z_1}
\frac{1}{\sqrt{2}}(\color{red}{-}\ket{\color{red}{1}0}+\ket{01})
\\
=\frac{1}{\sqrt{2}}(\ket{01}-\ket{10})
}
これの状態に逆Bell回路を適用すると
\displaylines{
\frac{1}{\sqrt{2}}(\ket{01}-\ket{10})
\xrightarrow[]{CX_{12}}
\frac{1}{\sqrt{2}}(\ket{01}-\ket{1\color{red}{1}})
\\
\xrightarrow[]{H_{1}}
\frac{1}{\sqrt{2}}\frac{1}{\sqrt{2}}(\ket{01}+\ket{11}-\ket{01}+\ket{11})
\\
=\frac{1}{\sqrt{2}}(2 \times \ket{11}) = \ket{11}
}
同様に波動の干渉で、$\ket{11}$が残ります。
まとめ
数式の方は若干冗長だったかもしれませんが、、
このように$braket$形式で数式を追うことで、逆Bell回路(Bell測定)により、
もつれ合ったBell状態から、基底状態に波動が収縮する状況が、
数式(数理モデル)上でも読み取れる点が、興味深いと考えます。
ちょっと長めの記事となり恐縮です。
最後に、本稿でイメージを掴んで頂き、実際の量子デバイスやシミュレータで動きを確認してみたい方は、ぜひ、AmazonBraketで学ぶ量子コンピュータ⑤を参照ください。