この記事について
量子コンピュータの勉強をはじめて最近一通りAmazonBraketを触り終えました。
最近登場したサービスであることもあり、少し丁寧なドキュメントを残しておくと後続の方が勉強しやすくなったり、参照してわからないところを調べる際に便利かなと思ったので
自分自身の理解向上も兼ねて記事にまとめていっています。
また、量子コンピュータ関係の他の記事は、下記で紹介しています。
※本記事は2021年2月に更新している記事です。更新などにより内容が変わっている可能性もあるのでご注意ください。
概要
本記事では量子コンピュータの導入部分に関して解説をしていこうと思います。
参照するのはこちらの4_Superdense_coding.ipynbというサンプルです。
こちらでは量子超高密度化という量子コンピュータで良く扱われる回路に触れた後、実際にAmazon Braket内でその回路を実装するというサンプルになっています。
なので今回は量子高密度符号化の説明をした後、実際のサンプルの説明に入っていこうかと思います。
Braketを使わずに、マウスで簡単に確認してみたい方は、下記も参照ください。
マウスだけ!で作る超高密度符号化実験
前提知識
こちらの4_Superdense_coding.ipynbというサンプルでは主に量子高密度符号化というものを扱っています。
量子高密度符号化というものは「1つのqubitだけを送信することで2つの古典的なビットを送信する方法」です。
送信者(アリス)は量子ゲートを適用した後の量子を受信者(ボブ)に送信することで受信者は2ビットの古典ビットのメッセージを復号できます。
量子高密度符号化
概要
量子高密度符号化というものは「1つのqubitだけを送信することで2つの古典的なビットを送信する方法」です。
まず最初のプロセスとしてアリスとボブは、もつれ状態のqubitのペア(つまり、ベル状態のペア)を共有する必要があります。
次に、アリスは、2つの古典ビットで送信する可能性のある4つのメッセージのうち、1つを選択します。
00, 01, 10, 11のうちの1つを選択するという意味です。
どの2ビット文字列を送信したいかに応じて、アリスは対応する量子ゲートを適用して、希望するメッセージを符号化します。
メッセージに対応する量子ゲートを適用した後、アリスはゲート適用後の自分の量子ビットをボブに送信し、ボブは最初のエンタングル処理を元に戻すことでメッセージを復号します。
流れ
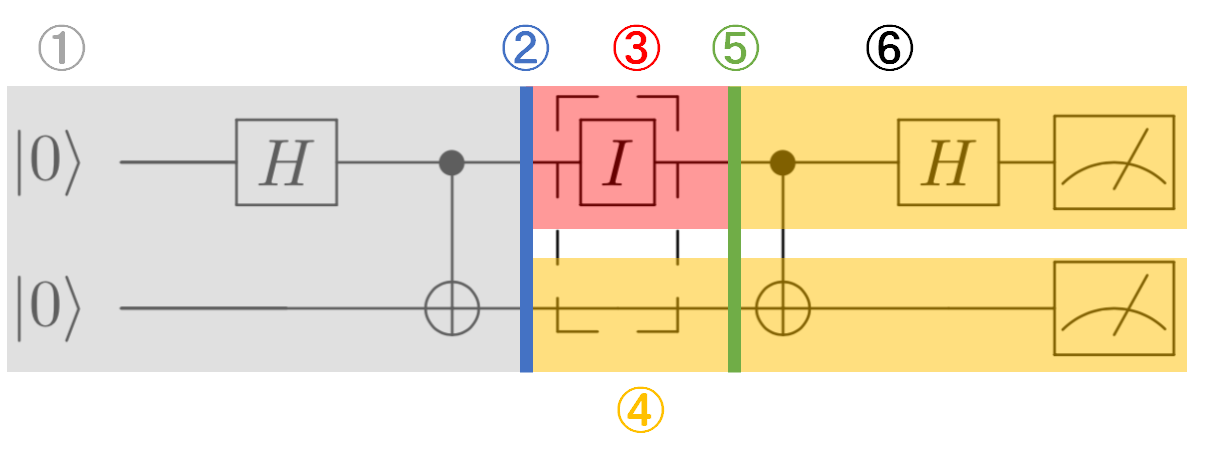
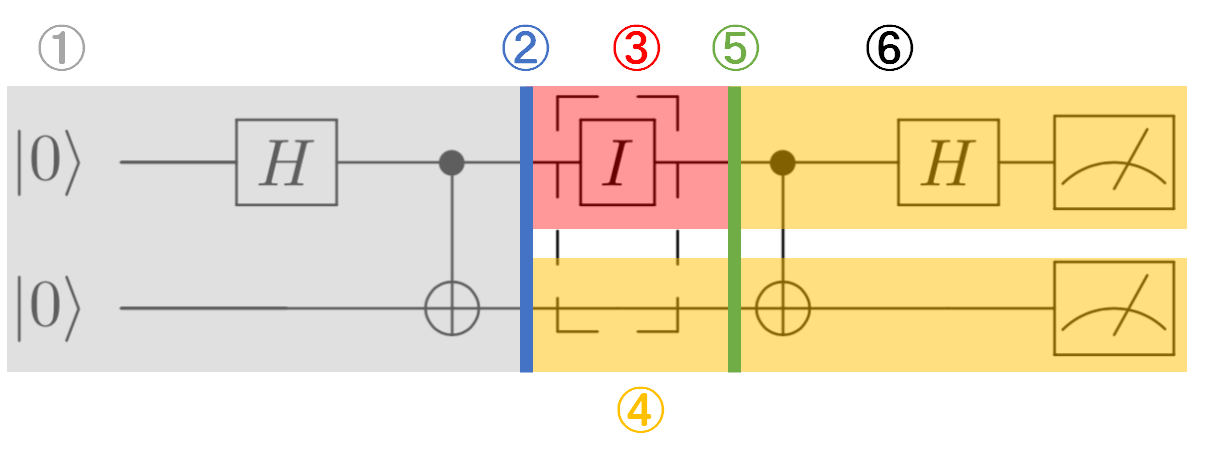
量子高密度符号化の流れを回路図とともに説明していきます。
まず流れをざっと示すと
①.ベルペア(もつれ状態にある2量子ビット)を用意します。ベルペアを用意するのは誰であっても構いません。アリスであってもボブであっても別の第三者であっても。今回は別の第三者が用意してくれたと仮定しましょう。
②.第三者が用意してくれたベルペアを何らかの方法でアリスとボブは共有します。つまり、片方をアリスがもう片方をボブが受け取ります。
③.アリスは受け取ったベル状態にある片方の量子ビットに対し、何らかの送りたいメッセージに対応する量子ゲート操作を行います。
④.ボブは量子ビットを受け取ったすぐのタイミングでは何もしません。
⑤.アリスはゲート操作を行った量子ビットを何らかの方法でボブに送信します。
⑥.アリスから送られてきた量子ビットをコントロールビットとして、自分の量子ビットをターゲットビットとしてCNOTゲートを適用し、アリスから送られてきた量子ビットにハダマードゲートを適用することによって、アリスの2ビットのメッセージをデコードします。
回路図で示すとそれぞれのプルセスに対応する図は以下のように示されます。
番号と対応づけて読んでいただけるとわかりやすくて良いかと思います。
では
③.アリスは受け取ったベル状態にある片方の量子ビットに対し、何らかの送りたいメッセージに対応する量子ゲート操作を行います。
ではどういった量子ゲート操作を行うのでしょうか?
実際に計算してみてアリスがどんなゲート操作を行うかを解き明かしていきましょう。
アリスの量子ゲート
まず結論から申し上げるとアリスは送りたいメッセージに対して以下のゲート操作を行います。
| Message | Alice's encoding |
|---|---|
| 00 | 𝐼 |
| 01 | 𝑋 |
| 10 | 𝑍 |
| 11 | 𝑍𝑋 |
これらの操作で本当に送りたいメッセージを送れるのかどうか解き明かしていきます。
00 を送る。
00 を送る場合を考えます。
上記 ② の時点でベル状態(もつれ状態)をアリスとボブは共有するのでこの時点での量子状態は
| 00 \rangle + | 11 \rangle
となります。(面倒なので規格化は無視して考えています。)
次に $I$ を適用するので
| 00 \rangle + | 11 \rangle \xrightarrow{I} | 00 \rangle + | 11 \rangle
となります。恒等変換なので何も変化なしですね。
この後CNOTを適用する。つまり、0量子ビット側(アリスビット側)が1の時、もう片方のビットを反転させます。
| 00 \rangle + | 11 \rangle \xrightarrow{I} | 00 \rangle + | 11 \rangle \xrightarrow{CNOT} | 00 \rangle + | 10 \rangle
そして最後にアリス側のビットにアダマールゲートを適用すると
| 00 \rangle + | 10 \rangle \xrightarrow{H} (| 0 \rangle + | 1 \rangle) | 0 \rangle + (| 0 \rangle - | 1 \rangle) | 0 \rangle = | 00 \rangle
となり、$| 00 \rangle$となることがわかります。
01 を送る。
01 を送る場合を考えます。
上記 ② の時点でベル状態(もつれ状態)をアリスとボブは共有するのでこの時点での量子状態は
| 00 \rangle + | 11 \rangle
となります。(今回も面倒なので規格化は無視して考えています。)
次に $X$ を適用するので
| 00 \rangle + | 11 \rangle \xrightarrow{X} | 10 \rangle + | 01 \rangle
となります。
この後CNOTを適用する。つまり、0量子ビット側(アリスビット側)が1の時、もう片方のビットを反転させます。
| 00 \rangle + | 11 \rangle \xrightarrow{X} | 10 \rangle + | 01 \rangle \xrightarrow{CNOT} | 11 \rangle + | 01 \rangle
そして最後にアリス側のビットにアダマールゲートを適用すると
| 11 \rangle + | 01 \rangle \xrightarrow{H} (| 0 \rangle - | 1 \rangle) | 1 \rangle + (| 0 \rangle + | 1 \rangle) | 1 \rangle = | 01 \rangle
となり、$| 01 \rangle$となることがわかります。
10 を送る。
そろそろ手を抜きますね笑
ベル状態を共有して$Z$を適用後、CNOTを適用するので以下の通りになります。
| 00 \rangle + | 11 \rangle \xrightarrow{Z} | 00 \rangle - | 11 \rangle \xrightarrow{CNOT} | 00 \rangle - | 10 \rangle
そして最後にアリス側のビットにアダマールゲートを適用すると
| 00 \rangle - | 10 \rangle \xrightarrow{H} | 10 \rangle
となり、$| 10 \rangle$となることがわかります。
11 を送る。
ベル状態を共有して$ZX$を適用後、CNOTを適用するので以下の通りになります。
| 00 \rangle + | 11 \rangle \xrightarrow{ZX} | 01 \rangle - | 10 \rangle \xrightarrow{CNOT} | 01 \rangle - | 11 \rangle
そして最後にアリス側のビットにアダマールゲートを適用すると
| 01 \rangle - | 11 \rangle \xrightarrow{H} | 11 \rangle
となり、$| 11 \rangle$となることがわかります。
アリスの量子ゲートまとめ
結果的にアリスの量子ゲートによって以下のようにまとめられることがわかるかと思います。
| Message | Alice's encoding | State Bob receives (non-normalized) |
After 𝐶𝑋 gate (non-normalized) |
After 𝐻 gate |
|---|---|---|---|---|
| 00 | 𝐼 | |00⟩ + |11⟩ | |00⟩ + |10⟩ | |00⟩ |
| 01 | 𝑋 | |10⟩ + |01⟩ | |11⟩ + |01⟩ | |01⟩ |
| 10 | 𝑍 | |00⟩ - |11⟩ | |00⟩ - |10⟩ | |10⟩ |
| 11 | 𝑍𝑋 | |01⟩ - |10⟩ | |01⟩ - |11⟩ | |11⟩ |
AmazonBraket
ここから実際にAmazonBraketを使って説明していきます。
環境を用意されていない方は、まずはこちらの記事やドキュメントなどを参考に環境を用意してください。
環境を用意すると以下のようにデフォルトでサンプルコードがGitHubからインポートされています。
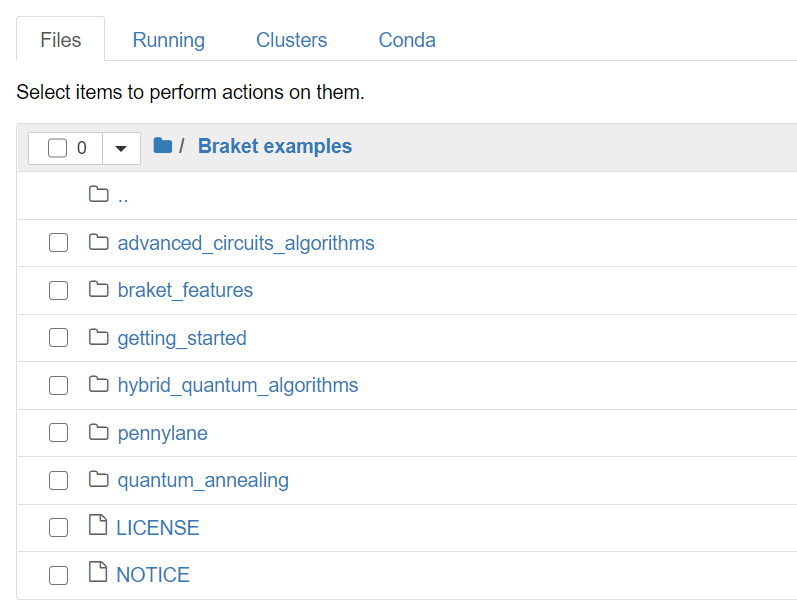
今回はこの配下にある
getting_started/4_Superdense_coding.ipynb
を見ていきます。
事前準備
事前準備として必要なものをいくつか解説していこうと思いましたが、特に特別なこともなさそうなのでここは割愛していきます。
Amazon Braketのサンプル上では
1.必要なモジュールをインポートしてきて、
2.S3バケットの登録
3.結果取得の関数定義(get_result)
を行っているのでそちらを見てみてください。
この記事のシリーズを読んでいただければそこまで難しい内容ではないかと思います。
本体
準備を終えたところで本体の方に入っていきます。
以下の図も意識しつつ、説明を見ていただける理解しやすいかと思います。
ベル状態の準備
まずはベル状態を準備します。(①)
circ = Circuit();
circ.h([0]);
circ.cnot(0,1);
アリスの量子ゲート
アリスは任意の量子ゲートを適用します。(③)
Amazon Braketのサンプルではアリスが適用できる量子ゲートを以下の通り、辞書型で用意しています。
# Four possible messages and their corresponding gates
message = {"00": Circuit().i(0),
"01": Circuit().x(0),
"10": Circuit().z(0),
"11": Circuit().x(0).z(0)
}
今回はまずは01を選んでそれをcirc回路に追加していきます。
# Select message to send. Let's start with '01' for now
m = "01"
# Encode the message
circ.add_circuit(message[m]);
復号
最後に復号します(⑥)
circ.cnot(0,1);
circ.h([0]);
回路図を見てみましょう。
print(circ)
出力結果
T : |0|1|2|3|4|
q0 : -H-C-X-C-H-
| |
q1 : ---X---X---
T : |0|1|2|3|4|
01を送る回路ができたと思います。
実行
実行してみます。
counts = get_result(device, circ, s3_folder)
print(counts)
キューにたまるのでしばらくは結果が返ってきませんが、
結果が返ってくると以下のような出力結果を得ることができます。
すべてのメッセージの送信
以下の通りループを組んであげることですべてのメッセージに対する検証を行うことができます。
for m in message:
# Reproduce the full circuit above by concatenating all of the gates:
newcirc = Circuit().h([0]).cnot(0,1).add_circuit(message[m]).cnot(0,1).h([0]);
# Run the circuit:
counts = get_result(device, newcirc, s3_folder)
print("Message: " + m + ". Results:")
print(counts)
実行してあげるとすべてのメッセージの結果を取得することができるので是非実行してみてください。
最後に
以上で「AmazonBraketで学ぶ量子コンピュータ⑤」を終わります。
今回は量子高密度符号化を行ってみることでサンプルを動かしてみました。
Braketを使わずに、マウスで簡単に確認してみたい方は、下記も参照ください。
マウスだけ!で作る超高密度符号化実験
また別記事で他のBraketサンプルの解説を行ないながら量子コンピュータを学んでいける記事を書いていくので是非見てみてください。