この記事について
前回までで、１量子系の操作を扱ってきましたがが、いよいよ２量子系の操作に入ります。
この量子テレポーテーションが、Bell回路による「もつれ合い」を理解するには良い題材と考えています。
量子テレポーテーションとはどんな操作なのかを、マウスだけで作ってみよう！
- 前半は、量子シミュレータをマウスで操作することで、量子回路を構成し
- 後半は、数式を用いて量子テレポーテーションの操作を追っていきます
一応、前半のマウス操作だけで理解できる構成にした(つもり)ですが、興味が湧いた方は、
後半の数式も参照頂ければと思います。
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}
量子テレポーテーションとは
量子状態（量子ビット１つ）を遠隔地に転送することを量子テレポーテーションといいます。
登場人物は３人です。
- 転送元で、送信したい量子状態を持つ 「送信者」
- 転送先で、上記量子状態を受信したい 「受信者」
- 送信者、受信者に対し、送信に必要なもつれ合った量子ビットを提供する「第三者」
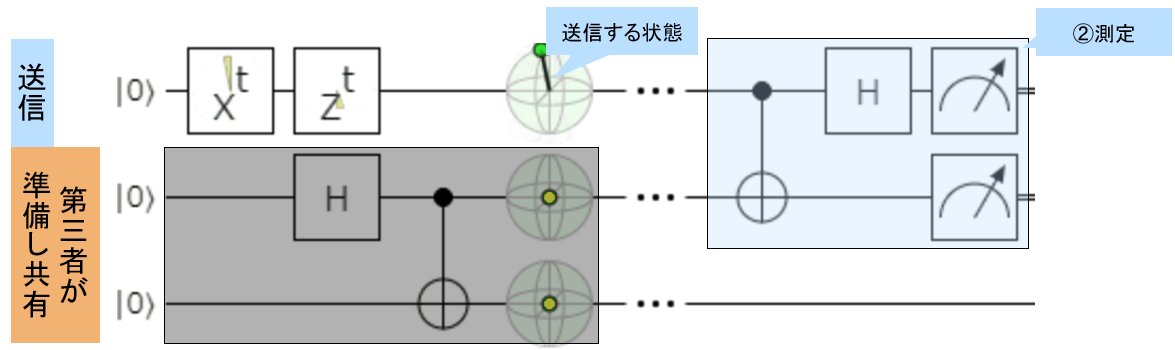
以降、どういった手順で量子状態を転送するかを図1 で示したいと思います。
処理の順序
処理は、下記の順序で進行します。
処理順序と図1 を対応して見ていただくとイメージが湧きやすいかと思います
- 第三者が「2量子のもつれあい」を作成、送信者と受信者に一つづつ共有
- 送信者が「送信したい量子状態」と「もつれあいの一方」をあわせて測定
- 送信者が「測定結果（古典2ビット）」を既存通信(メール等)を用いて受信者に連絡
- 受信者は「測定結果（古典2ビット）」に対応した量子ゲートを適用、量子状態を受信
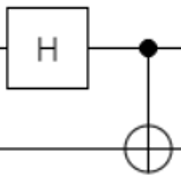
量子回路でも確認しておきましょう。
「H（アダマール）」とか、「測定（メータみたいな絵）」が出てきますが、上記と
やっていることは一緒です。①～④の対応を見ていただければ理解いただけると思います。
マウスで作る
では、実際に、上記量子回路をシミュレータ上で作成していきましょう。
使うものは、マウスだけです。
Quirk（シミュレータ）を開く
Quirk（シミュレータ）を起動します。下記のリンクを新しいタブで開いてください。
リンクを開くと、下記が画面が出てくるので、Edit Circuitをクリックしてください
①「第3者」が「もつれあい」を作成する
下記のマウス操作を真似て、パーツを配置してみてください。ポイントは、
- 1本目の線（量子ビット）は後でつかうので、2,3本目に配置してください。
- 「Xゲート」は、「$\oplus$」と表示されますが、同じ意味ですので気にしないでください。
うまくできなかった方は、下記リンクをクリックいただくと配置済みの状態が開けます。
こんな回路が出来上がった状況でです。
上記操作を細かく見ていきます。
| # | 回路 | 説明 |
|---|---|---|
| 1 |  |
これはブロッホ球と言い、量子ビットの状態を表現しています。 初期状態は、古典ビット(0/1)でいう0の状態で、上向きです。 量子状態を表現するbraket記法では、$\ket{0}$と表現します。 $\ket{0}$が２個あるので、$\ket{00}$と表現したりもします。 |
| 2 |  |
2つの量子ビットを「もつれあい」状態にするための回路です。 もつれあい状態（Bell状態）作ることから、Bell回路とも呼ばれます。 「$H$(アダマール)」と「CNOT（制御NOT）」組み合わせて作成します。 |
| 3 |  |
２つの量子ビットが「もつれあい状態」になりました。 もつれあい状態は単一の量子ビットでは表現できません この背景で、球の中心に黄色の点が存在する表現となっています。 |
②送信する量子状態 と もつれあいの一方 をあわせて測定
次に、送信者は、
- 自分が送信したい量子状態（量子ビット）を準備します。
- そして先程、第三者が準備した「もつれあいの一方」と上記を合わせて測定を行います。
うまくできなかった方は、下記リンクをクリックいただくと配置済みの状態が開けます。
こんな回路が出来上がった状況です。①で作成した範囲は、グレー塗りにしています。
上記操作を細かく見ていきます。
| # | 回路 | 説明 |
|---|---|---|
| 1 |  |
送信者が送信したい量子状態を準備するのですが、 わかりやすいように時間変化するような量子状態を準備しました。 このブロックは、一般的なものではなく、Quirk独自のもので、 ブロッホ球を縦方向と横方向に時々刻々と回転させる機能を持ちます |
| 2 |  |
先程の、Bell回路とは逆の構造をした逆Bell回路です。 2量子系に対するBell測定という測定を行うための回路です。 |
| 3 |  |
量子状態を測定し、古典ビット（00 or 01 or 10 or 11）を得ます 量子回路では、一本線は量子ビットの時間経過を表現します。 一方で、測定後は古典ビットの状態となり二重線で表現します。 |
③,④測定結果(古典2ビット)送信、ゲート適用による受信
冒頭、理解の為、下記を分けて記述していましたが、一緒に実装してしまいます。
３. 送信者が「測定結果（古典2ビット）」を既存通信を用いて受信者に送信
４. 受信者が「測定結果（古典2ビット）」に対応した量子ゲート操作で、量子状態を受信
うまくできなかった方は、下記リンクをクリックいただくと配置済みの状態が開けます。
こんな回路が出来上がった状況でです。
上記操作を細かく見ていきます。
| # | 回路 | 説明 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 |  |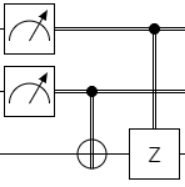
前述の測定により、量子状態が、00,01,10,11のいずれか確定します 縦の2重線はこの古典2ビットの受信者への古典通信に相当します。 受信者は、ビットパターンに応じて下記の量子ゲートを適用し、 送信者が送った量子状態を取り出すことができます。
|
出来上がった回路を眺める
最後に、出来上がった回路を眺めてみたいと思います。
- 第三者が「2量子のもつれあい」を作成、送信者と受信者に一つづつ共有
- 送信者が「送信したい量子」と「もつれあいの一方」をあわせて測定
- 送信者が「測定結果（古典2ビット）」を既存通信を用いて受信者に送信
- 受信者が「測定結果（古典2ビット）」に対応した量子ゲート操作で、量子状態を受信
の流れ、イメージだけでもご理解頂ければうれしいです。
ここまでのまとめ
量子テレポーテーションとはどういった操作かご理解頂けたでしょうか？
よく、
- 量子のもつれあい（Bellペア、EPRペア）を使うので光速度を超える通信が可能？？
といった議論を目にされるかもしれませんが、
上記手順をマウスで作成頂いた皆様には、そんなことは無い。と理解頂けたかと思います。
- 既存通信で古典２ビットを送信しなければ、受信者は量子状態を取り出せない
そうです。
この古典２ビットを送信する手段は、手紙でもEメールでも、光ファイバーでも何でもよいのですが、既存の通信手段を用いる事となります。
既存の高速通信は、一般に電磁波に依存しており、それらは光速度を超えることはできません。
本稿で、上記のような議論について、理解を深めて頂ければ、大変うれしいです。
なお、量子テレポーテーションと対となる操作である、超高密度符号化実験（Superdense coding）については下記記事で扱っているので合わせて参照頂ければ幸いです。
数式で確認する
では、引き続き、、
上記、シミュレータを使ってイメージは理解頂けたと思うのですが、最後に上記の手順を数式を使って追ってみようと思います。では行きましょう。
なお、量子ゲートの$braket$での演算に慣れていない方は先に、下記を参照ください。
①「第3者」が「もつれあい」を作成する
まずは、もつれあいをつくって行きます。
\displaylines{
\ket{000}
\xrightarrow[]{H_2}
\ket{0} \otimes \frac{1}{\sqrt{2}}(\ket{0} + \ket{1}) \otimes \ket{0}
\\
= \ket{0} \otimes \frac{1}{\sqrt{2}}(\ket{00} + \ket{10})
\\
\xrightarrow[]{CX_{23}}
\ket{0} \otimes \frac{1}{\sqrt{2}}(\ket{00} + \ket{1\color{red}{1}}) = \ket{0} \otimes \ket{B_{00}}
}
②送信する量子状態 と もつれあいの一方 をあわせて測定
送信したい量子状態を$\ket{\psi_{送信}} = a\ket{0}+b\ket{1}$ とすると
\displaylines{
\ket{\psi_{送信}} \otimes \ket{B_{00}}
\ \
=
\ \
(a\ket{0}+b\ket{1}) \otimes \frac{1}{\sqrt{2}}(\ket{00} + \ket{11})
\\
= \frac{1}{\sqrt{2}}(a\ket{000}+a\ket{011}+b\ket{100}+b\ket{111})
}
これに対し、上記の青掛かりのBell測定($CX_{12},H{1}$)を適用していきます。
まずは、$CX_{12}$を適用します。
\xrightarrow[]{CX_{12}}
\frac{1}{\sqrt{2}}(a\ket{000}+a\ket{011}+b\ket{1\color{red}{1}0}+b\ket{1\color{red}{0}1})
次に、$H_1$を適用しますが、少し複雑になります。先頭ビットの$\ket{0}と\ket{1}$に対して
$H$を適用するので、それぞれ、$H\ket{0} = \ket{+},H\ket{1} = \ket{-}$となり下記となります。
\displaylines{
\xrightarrow[]{H_{1}}
\frac{1}{\sqrt{2}}
(
\
\frac{a}{\sqrt{2}}(\ket{0}+\ket{1}) \otimes\ket{00}
\
+\frac{a}{\sqrt{2}}(\ket{0}+\ket{1}) \otimes\ket{11}
\\
+\frac{b}{\sqrt{2}}(\ket{0}-\ket{1}) \otimes\ket{10}
\
+\frac{b}{\sqrt{2}}(\ket{0}-\ket{1}) \otimes\ket{01}
\
)
\\
= \frac{a}{2}\ket{000}
+ \frac{a}{2}\ket{100}
+ \frac{a}{2}\ket{011}
+ \frac{a}{2}\ket{111}
\\
+ \frac{b}{2}\ket{010}
- \frac{b}{2}\ket{110}
+ \frac{b}{2}\ket{001}
- \frac{b}{2}\ket{101}
}
式を整理すると、
\displaylines{
= \frac{1}{2}\ket{00}(a\ket{0}+b\ket{1})
\\
+ \frac{1}{2}\ket{01}(a\ket{1}+b\ket{0})
\\
+ \frac{1}{2}\ket{10}(a\ket{0}-b\ket{1})
\\
+ \frac{1}{2}\ket{11}(a\ket{1}-b\ket{0})
}
そして、上記式を測定すると、各項の出現確率は、確率振幅の２乗の$1/4$の確率で、
下記のいずれかのパターンが出現することとなります。
| # | 確率が下記で、 | 送信者の量子状態が 下記のとき、 |
受信者は下記の 量子状態を観測する |
|---|---|---|---|
| 1 | $1/4$ | $\ket{00}$ | $a\ket{0}+b\ket{1}$ |
| 2 | $1/4$ | $\ket{01}$ | $a\ket{1}+b\ket{0}$ |
| 3 | $1/4$ | $\ket{10}$ | $a\ket{0}-b\ket{1}$ |
| 4 | $1/4$ | $\ket{11}$ | $a\ket{1}-b\ket{0}$ |
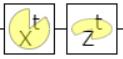
③,④測定結果(古典2ビット)送信、ゲート適用による受信
送信者が量子状態を観測した測定結果（古典２ビット）に応じ、ゲートを適用し、
受信者が量子状態を取り出すので、表で整理すると下記の通りとなります。
| # | 送信者の量子状態 | 受信者の量子状態 | 受信する 古典ビット |
適用する ゲート |
ゲート適用後状態 (受信する量子状態) |
|---|---|---|---|---|---|
| 1 | $\ket{00}$ | $a\ket{0}+b\ket{1}$ | 00 | ※なし | $a\ket{0}+b\ket{1}=\ket{\psi_{送信}}$ |
| 2 | $\ket{01}$ | $a\ket{1}+b\ket{0}$ | 01 | $X$ | 同上 |
| 3 | $\ket{10}$ | $a\ket{0}-b\ket{1}$ | 10 | $Z$ | 同上 |
| 4 | $\ket{11}$ | $a\ket{1}-b\ket{0}$ | 11 | $XZ$ | 同上 |
つまり、受信した古典ビットに合わせて（なし、$X、Z、XZ$）を適用することで受信者は、送信者が送信した量子状態$\ket{\psi_{送信}}$を得ることができます。
まとめ
マウスで量子テレポーテーションのイメージを掴むとともに、
数式でも送信者の準備した量子状態$\ket{\psi_{送信}}$を、受信者が受け取ることができる事を確認しました。
かなり冗長に記載したため、記事が長くなってしまい恐縮です。