マウスで量子誤り訂正（①ビットフリップ）

この記事について

ショアの量子誤り訂正符号を扱いたいのですが、分量が多くなりそうなので３回に分けて扱いたいと思います。

• ①：マウスで量子誤り訂正（①ビットフリップ）（本記事）
• ②：マウスで量子誤り訂正（②フェーズフリップ）
• ③：マウスで量子誤り訂正（③Shorの誤り訂正符号）

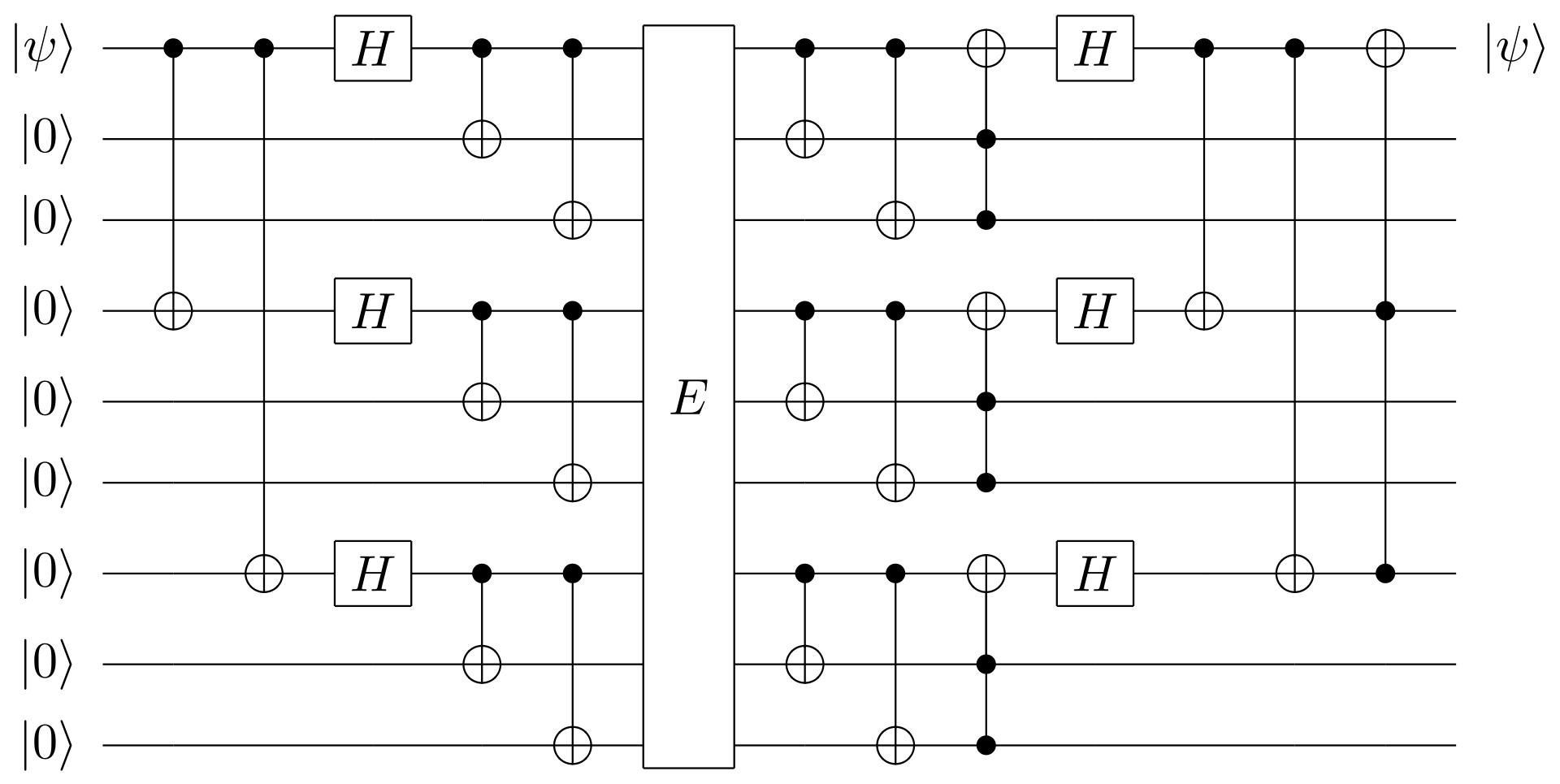
量子回路シミュレータのQuirkと数式の両方を使って進めて、最終的には、上記③で下記のShor Code¹が理解できるように、①、②を進めていきたいと思います。

• Shor's 9-bit Quantum Error Collection Code¹

また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。

% basic braket 
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1}  \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1}  \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}

量子誤り訂正の難しさ と 誤りの種類

難しさ

Nielsen & Chuang, Quantum Computation and Quantum Information² は、量子誤り訂正では、
下記３点が課題だと指摘しています。

• No cloning
• Errors are continuous
• Measurement destroys quantum information

一個ずつ見ていきましょう。

No cloning

「量子状態は、コピー・複製ができない」という量子複製不能定理が存在します。
誤りを訂正したい対象がコピーできるのであれば、量子状態をコピーし処理してから突き合わせを行えばエラーが訂正できますが、コピーそのものが不可能という点が、誤り訂正を困難にします。

Errors are continuous

ブロッホ球を想像いただくとわかりやすいですが、量子状態は連続的であるため、エラーも連続的で様々なパターン発生します。

古典ビット	量子ビット
0か1なので、誤りのバリエーションも少ない	単位球上の様々な位置を取るので、 誤りのパターンも連続的で訂正が難

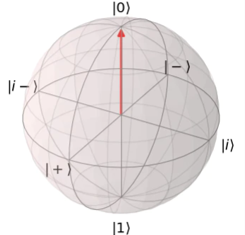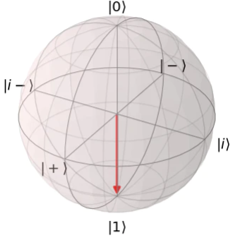
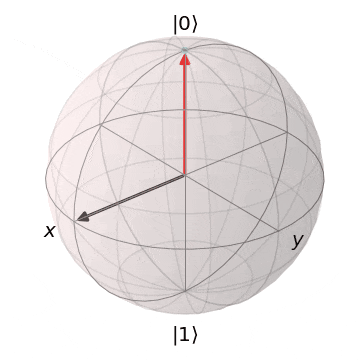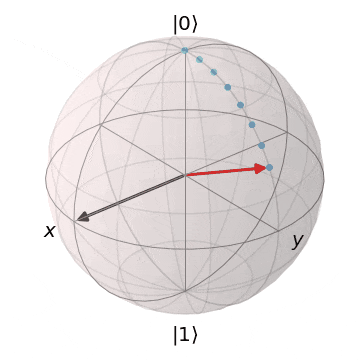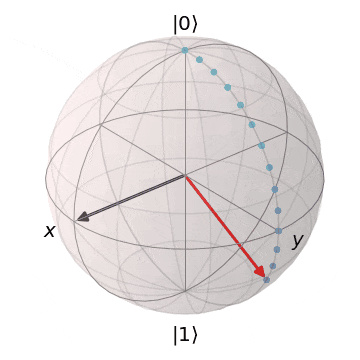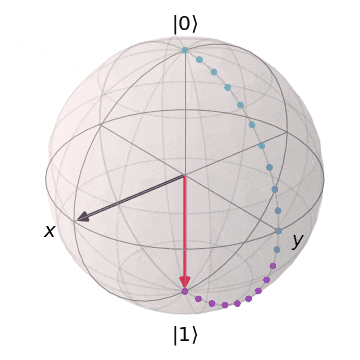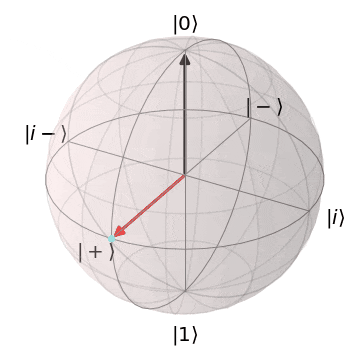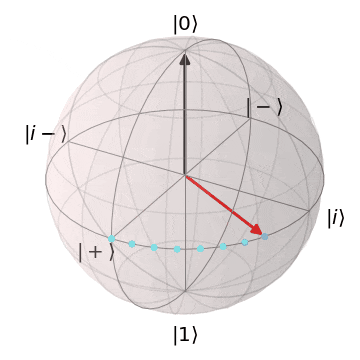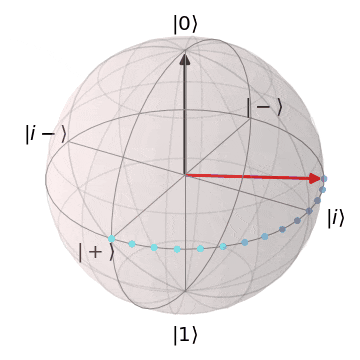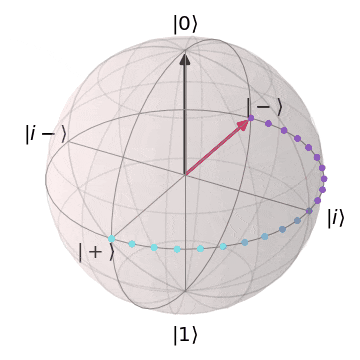
Measurement destroys quantum information

古典ビットにおける誤り訂正は、誤り対象対象データとパリティ等の誤り訂正符号を比較し、訂正を行います。これは、古典ビットにおいては誤り訂正データにいつでもアクセスできることが前提に成り立ちます。
一方、量子ビットの誤り訂正では、量子状態が測定により破壊される性質を持つため、量子状態を測定することなく（中身を知ることなく）誤りだけを、訂正する必要がある。

困難さ。伝わったでしょうか。

古典ビットと量子ビットの「誤り方」

誤り訂正の議論に入る前に、量子ビットではどんな種類の「誤り」が発生するのかを確認しておきます

古典ビット

下記のように符号反転（ビットフリップ）による誤りが、古典ビットでの「誤り方」です。

• 本来0だったものが、ノイズにより1になってしまった（0→1）
• 本来1だったものが、ノイズにより0になってしまった（1→0）

量子ビット

量子ビットでは、符号反転（ビットフリップ）に加え、位相反転(フェーズフリップ)が発生します。
具体的には下記に示すよう、パウリの$X,Z$ゲート相当の反転（フリップ）を想定します。

	符号反転 ビットフリップ	位相反転 フェーズフリップ
説明	古典ビットと同様の0,1の逆転です	古典には無い位相の逆転です 水平方向に反転します
イメージ
「誤り方」	$\ket{0}→\ket{1}$ $\ket{1}→\ket{0}$	$\ket{+}→\ket{-}$ $\ket{-}→\ket{+}$
パウリゲート でいうと	$pauli \ X$相当のエラー	$pauli \ Z$相当のエラー

ビットフリップエラーを訂正

まずは、符号が反転するビットフリップのエラー訂正から考えていきます。
Shorの誤り訂正符号は、下記のように複雑な形をしているのですが、これは、

• １量子ビット目の$\ket{\psi}$を、残りの8個の補助ビット$\ket{0}$を使って誤り訂正する回路です
• 誤りの種類として、上述のビットフリップ／フェーズフリップの両者を想定しています。
• 上記背景で、複雑な回路となっていますが、ビットフリップだけであれば３量子ビットで実現できます

よって、ビットフリップ／フェーズフリップ個別に誤り訂正回路を見ていきたいと思います。
なお、フェーズフリップについては、次回扱います。

• Shor's 9-bit Quantum Error Collection Code¹

ビットフリップ訂正回路

まずは、触っていただくのが良いと思います。下記リンクでシミュレータを起動できます。
下記は、ビットフリップエラーを想定して、ノイズとして$X$ゲートを適用しています。

• ビットフリップ訂正回路

上記、確認いただきたいのは、下記２点です。

• 誤り訂正が無い１量子ビット目は影響が出ます（ブロッホ球が反転します）
• 一方、誤り訂正がされた２量子ビット目は、誤り訂正されノイズ影響が無く処理できます

では、回路を細かく見ていきます。まず、量子ビットの使い方ですが、

• 1ビット目は、誤り訂正のは関係無い、説明用の量子ビットです。
• 2ビット目が、誤り訂正対象です。このビットを守るために誤り訂正回路を作ります。
• 3,4ビット目は、誤り訂正を実装するための、補助量子ビットです。

#	機能	回路	説明
1	エンコード		誤り訂正対象に、補助ビットをかけ合わせます。 下記のように、ノイズに強い状態をつくります。 この点については、詳細後述します。 $(a\ket{0}+b\ket{1})\otimes\ket{00} → a\ket{000}+b\ket{111}$
2	デコード		元の1ビット＋補助2ビットの状態に戻します。 3量子ビットのいずれかにノイズが発生した場合 デコード後の補助量子ビットに情報が保存されます $a\ket{000}+b\ket{111} → (a\ket{0}+b\ket{1})\otimes\ket{00}$
3	誤り訂正		補助量子ビットのパターンで、誤りが発生した 量子ビットが特定できます。 補助が11のときに保護対象のビットに パウリ$X$のノイズが乗っているので訂正します

何をエンコード、デコードしているか

エンコード回路

保護したい量子状態$\ket{\psi_{org}}$とした場合に、この$\ket{\psi_{org}}$は脆弱です。

\ket{\psi_{org}} = a\ket{0} + b\ket{1}

例えば、1ビットのパウリ$X_1$の反転が発生すると下記のようにビットが反転してしまいます。

X_1\ket{\psi_{org}} = a\ket{1} + b\ket{0} = b\ket{0} + a\ket{1}

と、$\ket{0}$と$\ket{1}$の確率振幅$a,b$が逆転してしまいました。
１量子ビット相当の情報（確率振幅$a,b$）を保全するための量子ビットとして、

• １量子ビットを用いて、１量子ビット相当の情報を扱うのは脆弱なので
• ３量子ビットを用いて、１量子ビット相当の情報を扱い、パウリ$X$への誤り耐性を高める

これがデコードです。
要は、３本の矢ですね。１本だと折れるが、３本なら折れない。

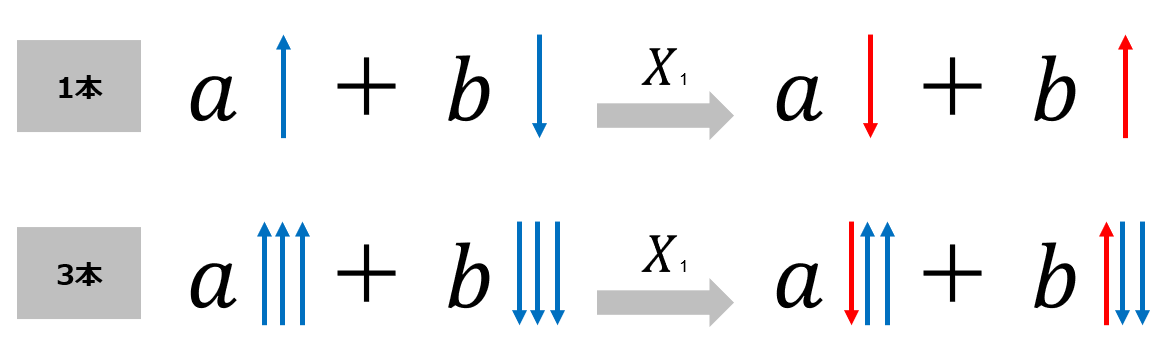
１量子ビット相当の情報（つまり、上記の$a,b$）を、あえて３量子ビットの$\ket{000},\ket{111}$を使って表現するためにはどうすれば良いでしょうか？

\ket{\psi_{enc}} = a\ket{000} + b\ket{111}

そうです。
$\ket{\psi_{org}}$を上記エンコード回路で処理することにより、上記の３本の矢の状態を作ることができます。

a\ket{000} + b\ket{100} \xrightarrow[]{CX12、13}a\ket{000} + b\ket{111} =\ket{\psi_{enc}}

この３本の矢の状態では、１ビットのビットフリップエラー（$X_1$)が発生すると、

X_1\ket{\psi_{enc}} = a\ket{000} + b\ket{111} \xrightarrow[]{X_1}a\ket{\color{red}{1}00} + b\ket{\color{red}{0}11}

と、赤いビットがフリップしますが、残り２ビットで、誤りを訂正可能です。

デコード回路

３本の矢状態の量子ビットにて、どのビットがエラーでフリップしたか？
誤りの場所を特定するのがデコード回路です。
エンコードされた量子状態$\ket{\psi_{enc}}$について、誤り訂正回路の1ビット目～3ビット目に、
パウリ$X$のエラーフリップが発生した状況を想定し、デコード回路を見ていきたいと思います。

エラー無しの状態をデコード回路($CX_{13,12}$)でデコードすると、下記のように、

• 保護したい量子状態$\ket{\psi_{org}}=a\ket{0} + b\ket{1}$と
• 補助ビット$\ket{00}$が取り出せます。

a\ket{000} + b\ket{111}
\xrightarrow[]{CX13、12}a\ket{000} + b\ket{100}
\ 
= 
\ a\ket{0} + b\ket{1} \ \otimes \ \ket{00}

次に誤り訂正回路の各ビットにパウリ$X$のエラーが発生した状況を整理します。

#	パウリ$X$エラーが 発生したビット	エラー発生後 デコード前の状態	デコード後の状態 （$CX_{13,12}$後）	補助ビットの状態
1	エラー無し ※上記の式	$a\ket{000} + b\ket{111}$	$a\ket{0} + b\ket{1} \ \otimes \ \ket{00}$	$\ket{00}$
2	１ビット目 (保護対象)	$a\ket{\color{red}{1}00} + b\ket{\color{red}{0}11}$	$a\ket{\color{red}{1}} + b\ket{0} \ \otimes \ \ket{11}$	$\ket{\color{red}{11}}$
3	２ビット目 (補助①)	$a\ket{0\color{red}{1}0} + b\ket{1\color{red}{0}1}$	$a\ket{0} + b\ket{1} \ \otimes \ \ket{10}$	$\ket{10}$
4	３ビット目 (補助②)	$a\ket{00\color{red}{1}} + b\ket{11\color{red}{0}}$	$a\ket{0} + b\ket{1} \ \otimes \ \ket{01}$	$\ket{01}$

保護対象の量子ビットでの、パウリ$X$エラーによるビットフリップの検知を検討します。
補助量子ビットに着目すると状態が$\ket{11}$のとき、1ビット目は$a\ket{1}+b\ket{0}$と、
ビットフリップした状態となっています。（上記#2）

つまり、誤り訂正では、

• 補助量子ビットが、$\ket{11}$のときに（これを条件として）
• パウリ$X$にて、ビットフリップを誤り訂正する

という操作が必要になります。２つの補助量子ビットを条件としてパウリ$X$ゲートを適用する。
そうです。誤りの訂正には、トフォリゲートを用います。

誤り訂正

上記の#2のときに、トフォリゲートにより誤り訂正で、どういった状態となるかを計算で確認しておきたいと思います。デコード後の状態から計算すると、

\displaylines{
a\ket{\color{red}{1}} + b\ket{0} \ \otimes \ \ket{11}
\xrightarrow[]{CCX_{23→1}}
X(a\ket{\color{red}{1}} + b\ket{0}) \ \otimes \ \ket{11}
\\
=a\ket{0}+b\ket{1} \ \otimes \ \ket{11} 
\ \ 
= 
\ \ 
\color{red}{\ket{\psi_{org}}} \otimes \ket{11} 
}

となり、トフォリゲート適用で、保護対象ビットの元の状態$\ket{\psi_{org}}$を取り出すことができました。

まとめ

今回は、パウリ$X$エラーを想定した場合の誤り訂正回路について見ていきました。
最後に概要をまとめておくと、

• エンコードにて３本の矢の状態を作り出す
• デコードにて、パウリ$X$エラーが発生したビットの場所の情報を補助ビットに書き出す
• 誤りが、保護対象の１ビット目であった場合にのみ、訂正回路で誤りを訂正する

ぜひ、皆さんもマウスで、誤り訂正が行われる状況を、体感頂ければと思います。
②フェーズフリップ、③Shorの誤り訂正符号は、次回以降で扱っていきます。

• ビットフリップ訂正回路

おまけ

上記の誤り訂正回路が、冒頭の課題をどのように解消しているかを確認しておきます。

No cloning

保護対象$\ket{\psi}$をコピーすることはできません。
ですので、$\ket{\psi}$のパウリ$X$エラー耐性を高める目的で補助ビットを用います。

Errors are continuous

実をいうと、180度回転以外の回転角度のエラーにも対応しています。
シミュレータで、ノイズとして、$X$だけでなく、$X^{\frac{1}{2}}$,$X^{\frac{1}{4}}$等を適用しても誤り訂正可能です

• ノイズがX^(1/2)

• ノイズがX^(1/4)

• ノイズが時間変化

Measurement destroys quantum information

3量子ビット全てを測定すると、量子状態は破壊されますが、
補助ビットのみ測定することで、量子状態を破壊しない誤り訂正が可能です。

次回は、

マウスで量子誤り訂正（②フェーズフリップ）で、位相フリップの誤り訂正を扱います。

おまけのおまけ(ノイズX^1/2の計算）

下記のノイズがX^(1/2)のパターンに関して、計算過程を下記に整理します。
計算方法は、ある勉強会で、お詳しい方に伺ったものです。ありがとうございます

$X$は下記のようにアダマール基底で書き下す事ができます

X = \ketbras{+}{+}-\ketbras{-}{-}

また、$X^{1/2}$を計算すると下記となります。
詳細は、分数ゲート? の計算方法をご確認ください。

X^{\frac{1}{2}}=\frac{1 \pm i}{2}\ketbra{0}{0}+\frac{1 \mp i}{2}\ketbra{0}{1}+\frac{1 \mp i}{2}\ketbra{1}{0}+\frac{1 \pm i}{2}\ketbra{1}{1}

よって、

\displaylines{
X^{\frac{1}{2}}\ket{0} = \frac{1 \pm i}{2}\ket{0} + \frac{1 \mp i}{2}\ket{1}
\\
X^{\frac{1}{2}}\ket{1} = \frac{1 \mp i}{2}\ket{0} + \frac{1 \pm i}{2}\ket{1}
}

ビットフリップ訂正回路を計算すると、

\displaylines{
\ket{\psi_{org}} = a\ket{0} + b\ket{1}
\xrightarrow[]{CX12,13(Encode)}
a\ket{000}+b\ket{111}
\\
\xrightarrow[]{X^{\frac{1}{2}}(Noize)}
\frac{1}{2}\left[\ 
a(1 \pm i)\ket{000} + 
a(1 \mp i)\ket{100} +
b(1 \mp i)\ket{011} +
b(1 \pm i)\ket{111}
 \right]
\\
\xrightarrow[]{CX_{12, 13}(Decode)}
\frac{1}{2}\left[\ 
a(1 \pm i)\ket{000} + 
a(1 \mp i)\ket{111} +
b(1 \mp i)\ket{011} +
b(1 \pm i)\ket{100}
 \right]
\\
\xrightarrow[]{CCX_{23→1}(Collect)}
\frac{1}{2}\left[\ 
a(1 \pm i)\ket{000} + 
a(1 \mp i)\ket{011} +
b(1 \mp i)\ket{111} +
b(1 \pm i)\ket{100}
 \right]
}

上記式を整理すると、下記の通り誤り訂正により$\ket{\psi_{org}}$を取り出すことができました。

(a\ket{0}+b\ket{1})(\frac{1 \pm i}{2}\ket{00}+\frac{1 \mp i}{2}\ket{11})
 = \ket{\psi_{org}} \otimes (\frac{1 \pm i}{2}\ket{00}+\frac{1 \mp i}{2}\ket{11})

1. https://en.wikipedia.org/wiki/Quantum_error_correction#The_Shor_code より引用 ↩ ↩² ↩³

2. Nielsen & Chuang,Quantum Computation and Quantum Information, p.427 ↩