この記事について
下記①②にて、ビットフリップとフェーズフリップの訂正回路を確認しました。
本稿では、これらを組み合わせて、Shorの誤り訂正符号を確認していきましょう。
- ①:マウスで量子誤り訂正(①ビットフリップ)
- ②:マウスで量子誤り訂正(②フェーズフリップ)
- ③:マウスで量子誤り訂正(③Shorの誤り訂正符号)(本記事)
今回も、量子回路シミュレータのQuirkと数式の両方を使って進めます。
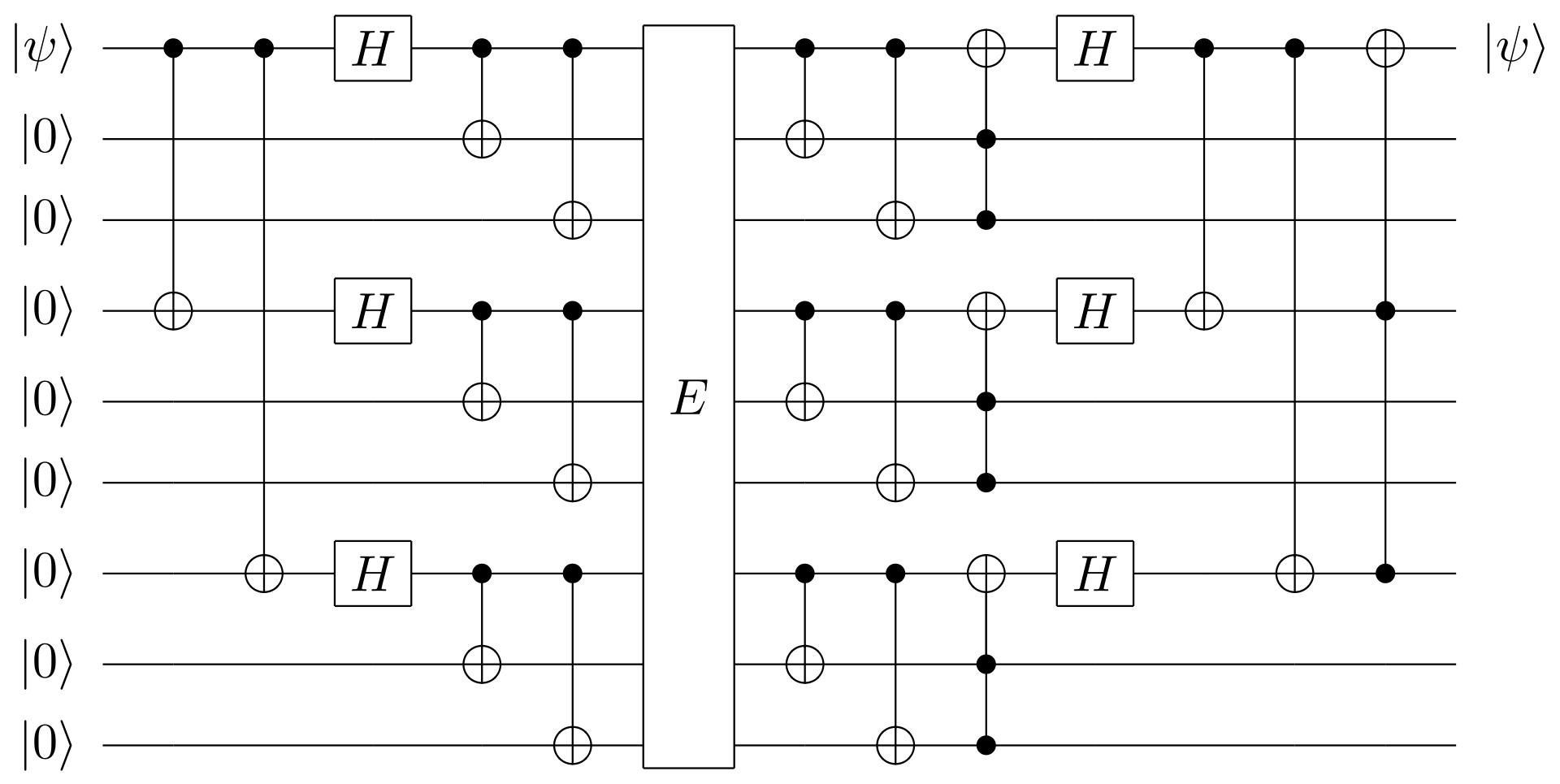
- Shor's 9-bit Quantum Error Collection Code1
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}
ビットフリップとフェーズフリップの訂正
まずは、ビットフリップとフェーズフリップの訂正回路を復習しておきます。
ビットフリップ訂正回路@Quirk

フェーズフリップ訂正回路@Quirk

エンコードの違い
こちらも復習で、ビットフリップ訂正・フェーズフリップ訂正のエンコードは下記の通りでした。
\displaylines{
\ket{\psi_{Benc}} = a\ket{000} + b\ket{111}
\\
\ket{\psi_{Penc}} = a\ket{{\tiny +++}}+b\ket{{\tiny ---}}
}
ビットはパウリ$X$エラー、フェーズはパウリ$Z$エラーに対処するために、それぞれ計算基底とアダマール基底を用いて量子状態をエンコードする。
そして、フェーズはパウリ$Z$エラーに対応するアダマール基底を用いたエンコードのため、$H$(アダマールゲート)が掛かるのがフェーズフリップ訂正のエンコード回路でした。
| エンコード | デコード | |
|---|---|---|
| フェーズフリップ 訂正 |
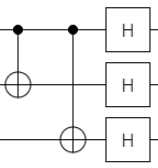 |
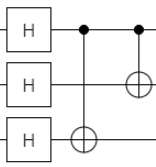 |
| ビットフリップ 訂正 |
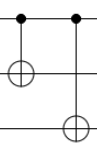 |
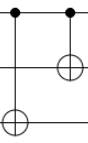 |
ビット、フェーズの両方の誤りに対応する
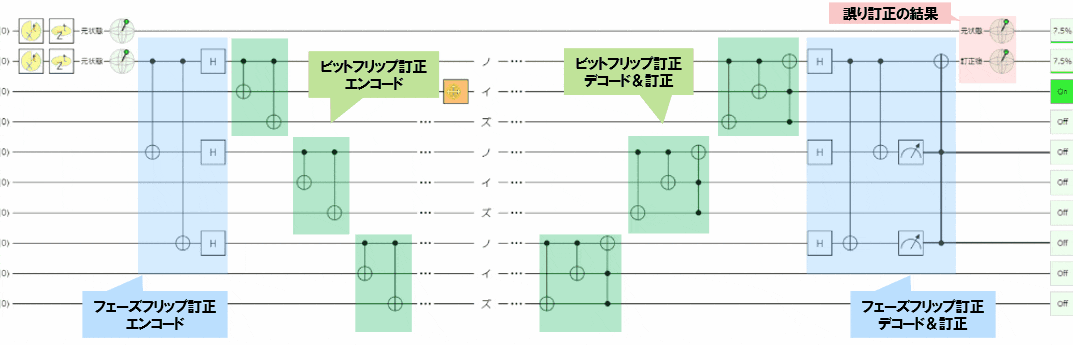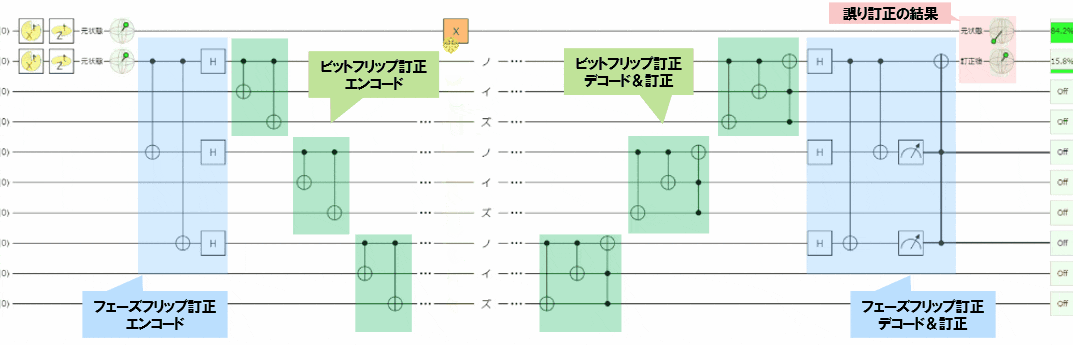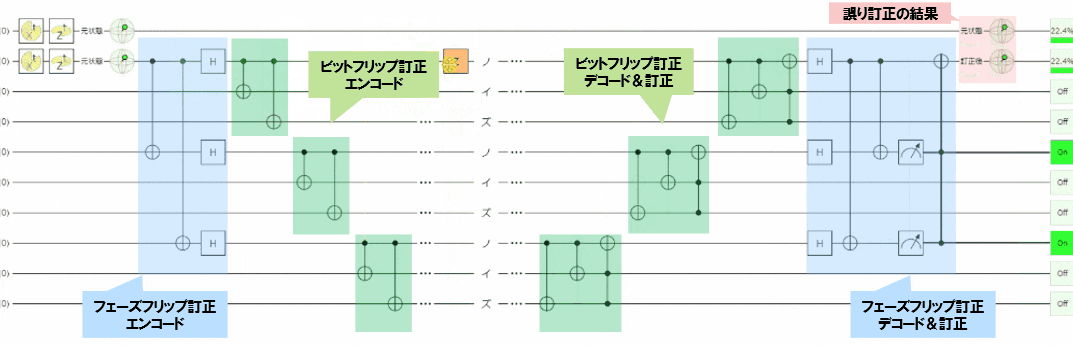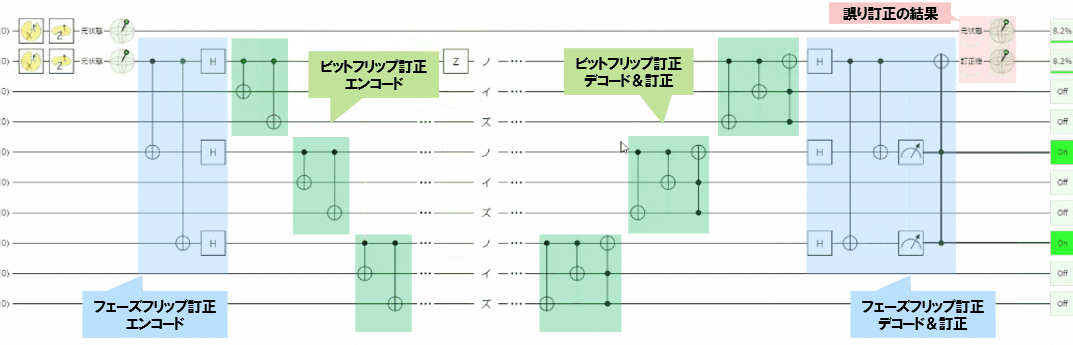
Shorの量子誤り訂正回路@Quirk
上記の2回路を組み合わせたのがShorの量子誤り訂正回路です。
ビットフリップ、フェーズフリップの両方の誤りに対し、エラー訂正が可能です。
構成を見ていくと、
- まず、エンコードに$H$が係るフェーズフリップ訂正のエンコードを行います。
- フェーズフリップ訂正は3量子ビットで行いますが、この3つのビットそれぞれにビットフリップ訂正のエンコード、デコード、訂正を行います。
- そして、ビットフリップの訂正終了後に、最後にフェーズフリップのデコード、訂正を行います。
- 上記見ていただくとわかるのですが、
- パウリ$X$エラー、パウリ$Z$エラーどちらが発生しても誤り訂正が行えます
- そして、1量子系の任意角度(パウリ$XZ$)エラーを訂正を行うことができます(※次節で後述)
- まさに、Nielsen & Chuang2が指摘する「Errors are continuous」に対処しています
任意のエラーに対応できるか?
補足として、上記の※を扱っておきます。
任意のエラーとは、ブロッホ球を想像していただくとわかりやすいのですが、元の状態$\ket{\psi_{org}}$に対して、X軸回転、Z軸回転、Y軸回転と任意軸の任意角度の回転が発生することを意味します。
この1量子系に対する任意角度の回転によるノイズ$\varepsilon_1$は、パウリゲートを用いると下記のように表現できます。
(下記4つのパウリゲートにて任意角度の回転が実現できるため。)
\varepsilon_1 = e_0I + e_1X_1 + e_2Z_1 + e_3X_1Z_1
\ \ \ \ \
e_n \in \mathbb{C}
上記式は、ノイズ$\varepsilon_1$が状態$\ket{\psi_{org}}$に発生すると、$\varepsilon_1\ket{\psi_{org}}$となり、ノイズ発生後の状態が、$I,X,Z,XZ$の重ね合わせ状態として表現されます。
この重ね合わせ状態は、測定により$I,X,Z,XZ$のいずれかに収縮し、これらのパウリ操作で訂正が可能された離散化されたエラー状態に収縮します。
つまり、パウリ$X$とパウリ$Z$に対するエラー訂正ができれば任意の$\varepsilon_1$に対する誤り訂正が可能となり、これを実現するのがShorの誤り訂正符号となります。
まとめ
Shorの9-bit Quantum Error Collection Codeを扱いました。
- 1量子ビットの量子状態(つまり確率振幅$a,b$)を保護するために、補助量子ビット8ビットを用いてビットフリップ、フェーズフリップに耐性を持つ誤り訂正回路を構成しました。
- 量子ビットは、コピーできない、観測で破壊されるという背景から、補助量子ビットはフリップに対する耐性を増すための3本の矢として活用し、誤り耐性を実現しました。
- Stabilizer符号等のより効率性が高い符号も存在しますが、量子誤り訂正のアウトラインを理解する意味では、Shor's Codeは良い題材だと思います。今後、他の誤り訂正符号も紹介したいと思います。