この記事について
前回は、①のビットフリップ訂正回路をあつかいました。
今回は、これを拡張し、フェーズフリップ（位相反転）の訂正回路を議論したいと思います。
- ①：マウスで量子誤り訂正（①ビットフリップ）
- ②：マウスで量子誤り訂正（②フェーズフリップ）(本記事)
- ③：マウスで量子誤り訂正（③Shorの誤り訂正符号）
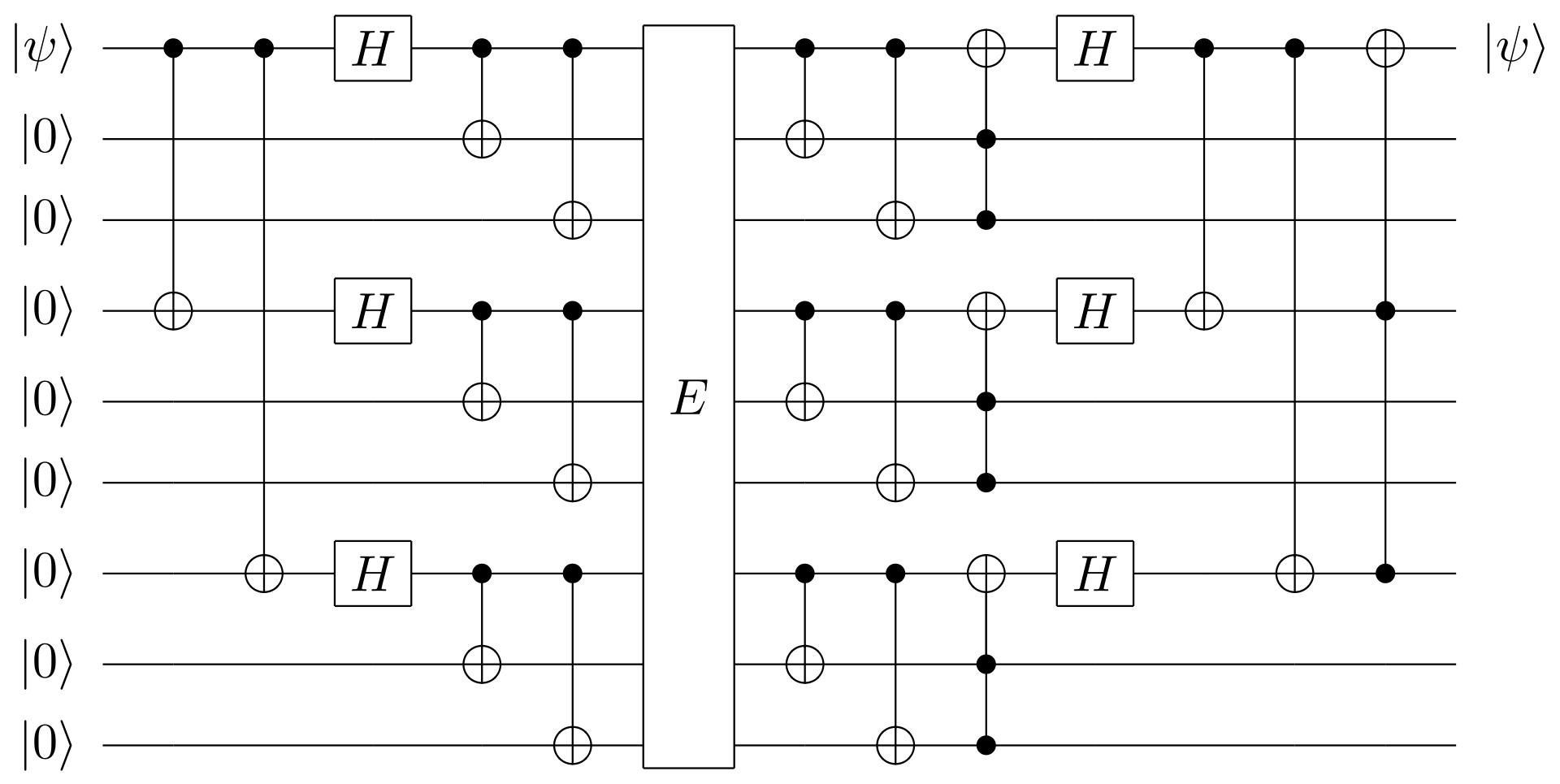
量子回路シミュレータのQuirkと数式の両方を使って進めて、最終的には、上記③で下記のShor Code1が理解できるように進めていきたいと思います。
- Shor's 9-bit Quantum Error Collection Code1
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\tate}[2]{\begin{bmatrix} #1 \\ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \\ #3 & #4 \end{bmatrix}}
量子ビットの「誤り方」
前回のおさらいです。前回は、ビットフリップ（符号反転）の誤り訂正を扱いました。
今回は、フェーズフリップ（位相反転）の誤り訂正を扱っていきます。
| ビットフリップ（符号反転） | フェーズフリップ（位相反転） 今回はこちら |
|
|---|---|---|
| 説明 | 古典ビットと同様の0,1の逆転です | 古典には無い位相の逆転です 水平方向に反転します |
| イメージ |  |
 |
| 「誤り方」 | $\ket{0}→\ket{1}$ $\ket{1}→\ket{0}$ |
$\ket{+}→\ket{-}$ $\ket{-}→\ket{+}$ |
| パウリゲート でいうと |
$pauli \ X$相当のエラー | $pauli \ Z$相当のエラー |
フェーズフリップ訂正回路
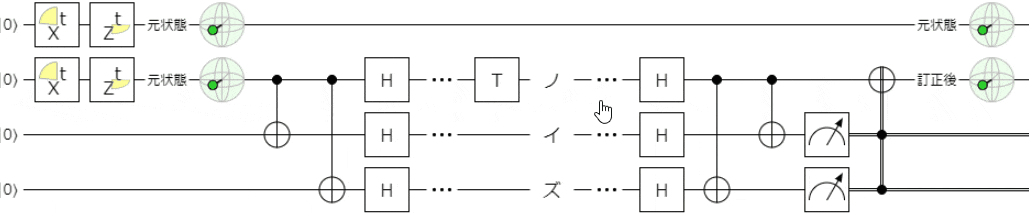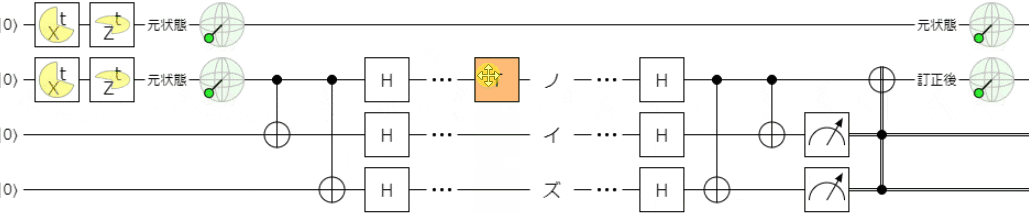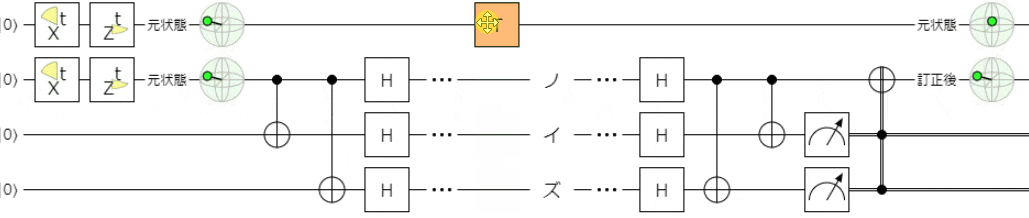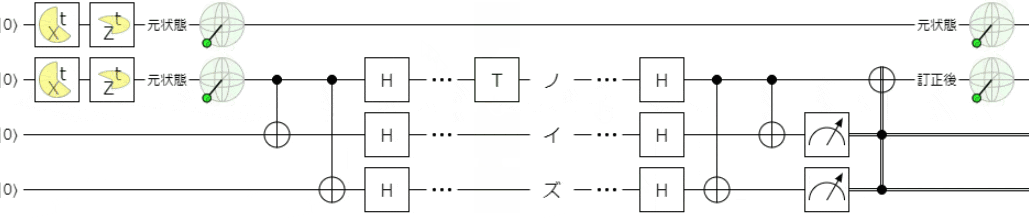
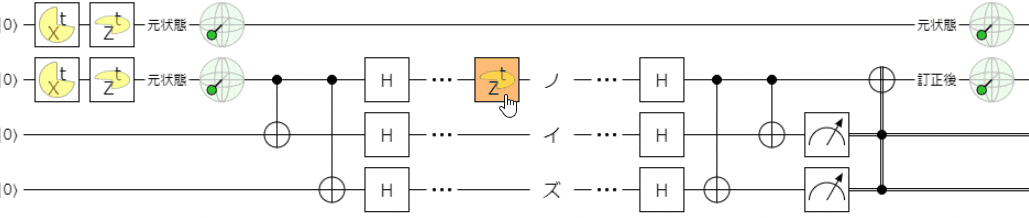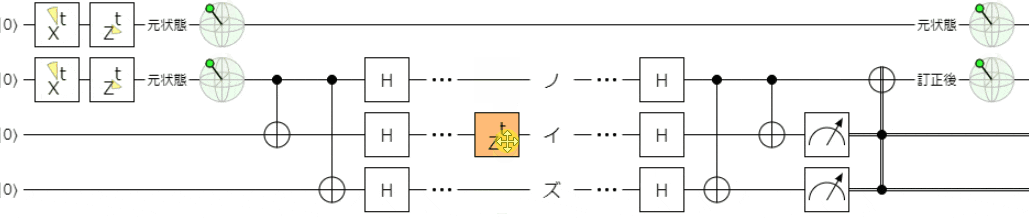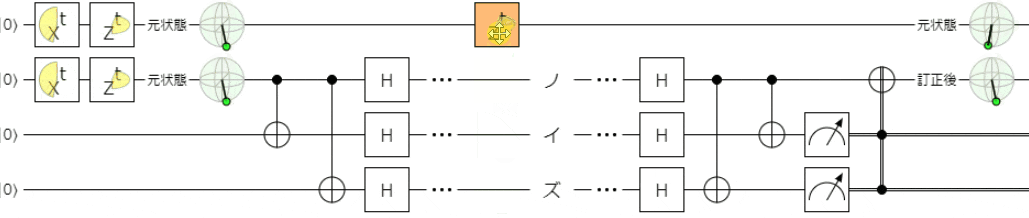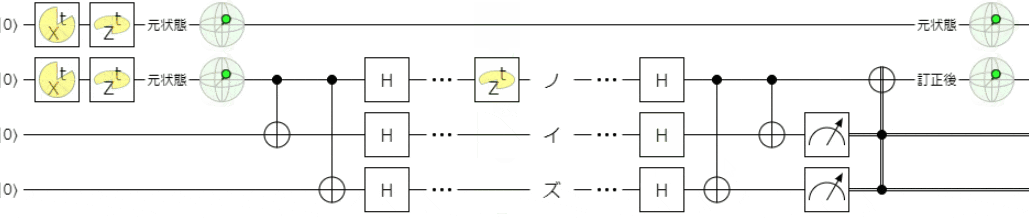
まずは、触っていただくのが良いと思います。下記リンクでシミュレータを起動できます。
下記は、フェーズフリップエラーを想定して、ノイズとして$Z$ゲートを適用しています。
前回と同様に、
- 誤り訂正が無い１量子ビット目は影響が出ます（ブロッホ球が反転します）
- 一方、誤り訂正がされた２量子ビット目は、誤り訂正されノイズ影響が無く処理できます
では、回路を細かく見ていきます。まず、量子ビットの使い方ですが、
- 1ビット目は、誤り訂正のは関係無い、説明用の量子ビットです。
- 2ビット目が、誤り訂正対象です。このビットを守るために誤り訂正回路を作ります。
- 3,4ビット目は、誤り訂正を実装するための、補助量子ビットです。
ビットフリップ訂正との差分
前回扱った、ビットフリップ訂正回路との違いは、エンコード、デコード処理です。
比較すると下記の通りで、すべての量子ビットに対してエンコード／デコードともに
$H$（アダマール）を掛けている点が違いです。
| エンコード | デコード | |
|---|---|---|
| フェーズフリップ 訂正 |
 |
 |
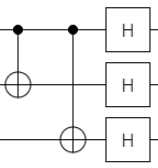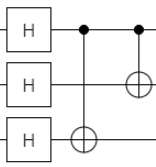| ビットフリップ 訂正 |
 |
 |
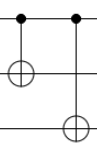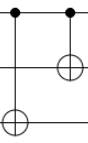なぜ、Hを掛けるのか？
それは、3本の矢の作り方が違うからです。
前回扱った、ビットフリップ訂正回路を思い出しましょう。
ビットフリップ訂正は、パウリ$X$エラー（$\ket{0}→\ket{1}$とその逆）に強いエンコードを考えました。
\ket{\psi_{enc}} = a\ket{000} + b\ket{111}
$\ket{0}$が１本よりは、３本のほうが誤りにも強いだろうという考え方です。
では、フェーズフリップのパウリ$Z$エラー（$\ket{+}→\ket{-}$とその逆）訂正に向け
- どういったエンコードにすれば良いでしょうか？言い方をかえると、、
- 守りたい確率振幅（$a,b$）はどういった状態ベクトルに持たせるべきでしょうか？
パウリ$Z$エラー（$\ket{+}→\ket{-}$とその逆）に耐えるためには、
下記のようにアダマール基底を用いたエンコードが必要です。
\ket{\psi_{enc}} = a\ket{{\scriptsize +++}}
\
+
\
b\ket{{\scriptsize ---}}
つまり、エンコード後の状態が上記の様なアダマール基底を用いたエンコードとなるように、$H$を適用するのがフェーズフリップ訂正回路です。
保護対象の量子ビットの状態を$\ket{\psi}$とすると、下記のようにエンコード回路を用いてアダマール基底を用いたエンコード状態を作ることができます。
\ket{\psi} \otimes \ket{00}
\xrightarrow[]{CX_{12、13}}
a\ket{000} + b\ket{111}
\xrightarrow[]{H_{123}}
a\ket{{\scriptsize +++}}
\
+
\
b\ket{{\scriptsize ---}}
= \ket{\psi_{enc}}
デコード回路
一応、前回と同様にデコードの過程と、誤り訂正の適用条件を確認しておきますが、エンコードされた状態の基底が変わるだけで、デコード後の状態や誤り訂正の適用条件も同様です。
| # | パウリ$Z$エラーが 発生したビット |
エラー発生後 デコード前の状態 |
デコード後の状態 （$H_{123}CX_{13,12}$後） |
補助ビットの状態 |
|---|---|---|---|---|
| 1 | エラー無し ※上記の式 |
$a\ket{{\scriptsize +++}} + b\ket{{\scriptsize ---}}$ | $a\ket{0} + b\ket{1} \ \otimes \ \ket{00}$ | $\ket{00}$ |
| 2 | １ビット目 (保護対象) |
$a\ket{{\scriptsize \color{red}{-}++}} + b\ket{{\scriptsize \color{red}{+}--}}$ | $a\ket{\color{red}{1}} + b\ket{0} \ \otimes \ \ket{11}$ | $\ket{\color{red}{11}}$ |
| 3 | ２ビット目 (補助①) |
$a\ket{{\scriptsize +\color{red}{-}+}} + b\ket{{\scriptsize -\color{red}{+}-}}$ | $a\ket{0} + b\ket{1} \ \otimes \ \ket{10}$ | $\ket{10}$ |
| 4 | ３ビット目 (補助②) |
$a\ket{{\scriptsize ++\color{red}{-}}} + b\ket{{\scriptsize --\color{red}{+}}}$ | $a\ket{0} + b\ket{1} \ \otimes \ \ket{01}$ | $\ket{01}$ |
まとめ
前回に引き続き、誤り訂正回路を扱いました。
フェーズフリップの訂正回路は、
- フェーズフリップがどの様な誤りなのか？
- その誤りにはどういったエンコードが強いのか？
を検討することで、
比較的簡単にフェーズフリップ訂正回路にたどり着くことができたかと思います。
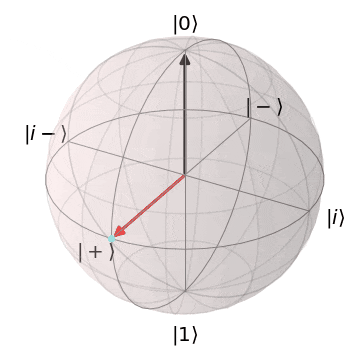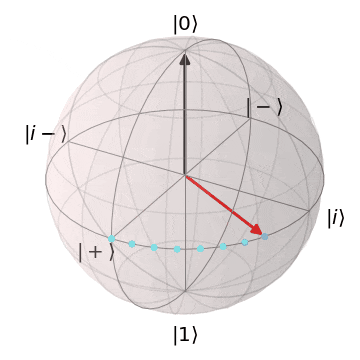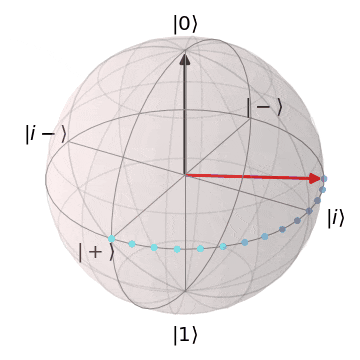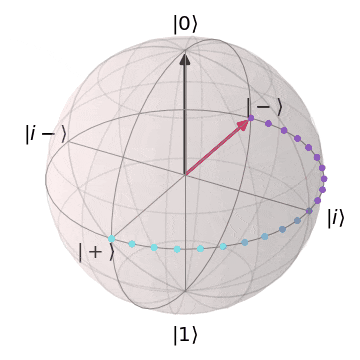
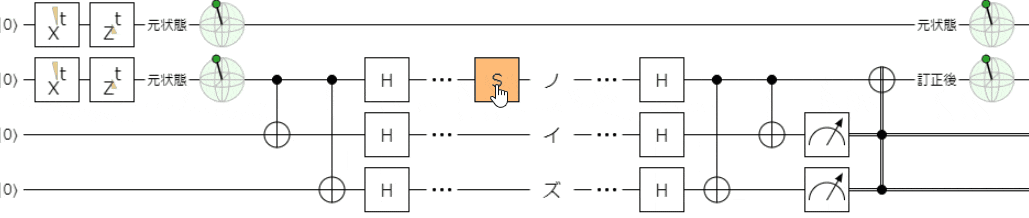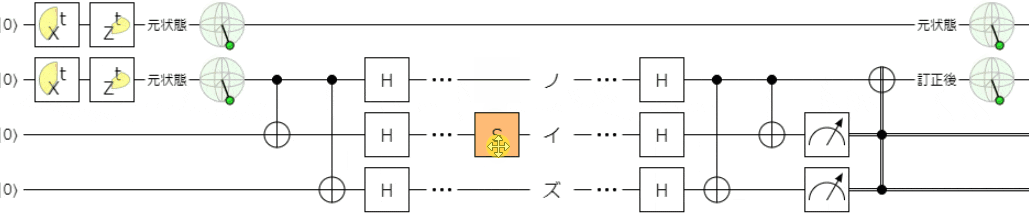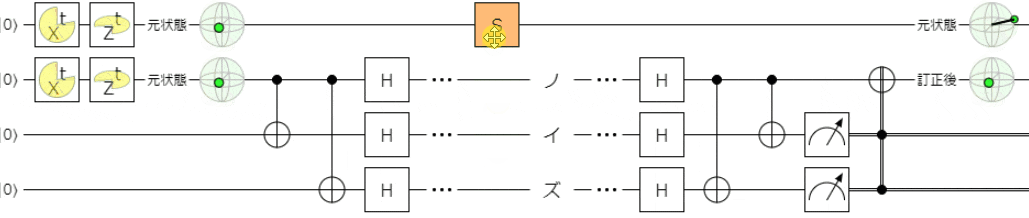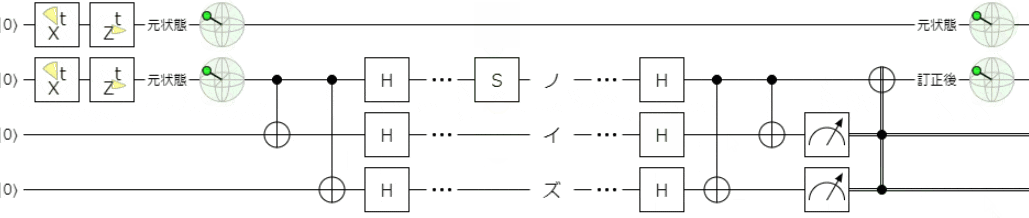
最後に、前回と同様に、フェーズフリップ（パウリ$Z$）に関して、
ノイズが$Z^{\frac{1}{2}}(=S)$や$Z^{\frac{1}{4}}(=T)$、$Z$軸回転で時間変化するパターン
においても正しく誤り訂正ができることを確認しておこうと思います。
次回は、
マウスで量子誤り訂正（③Shorの誤り訂正符号）で、ビット、フェーズの両方のフリップに対応できるShorの符号を扱います。