前回、前々回でディープラーニングを使った「画像」の異常検知を行いました。
今回は、同じ技術を使って「音」の異音検知をやってみます。
ディープラーニングは音声認識でも良い成績を示しています。
カメラvsマイク
製造業では、カメラよりマイクを使ってセンシングしたいという要望も多く聞かれます。
その理由は以下が考えられます。
- スペースの問題でカメラが設置できない(狭い、遮蔽物がある)
- 過酷な環境のためカメラが設置できない(高温、加工油がかかる)
カメラは直接物体を捉えなければいけませんが、マイクは間接的な音の伝わりでも拾えるため、非常に汎用性があるセンサといえるでしょう。
データセット
使うデータはESC-50です。
これは、人の音声や自然界の音を集めたデータで、50個のラベルが付与されています。
正常データと異常データの選定
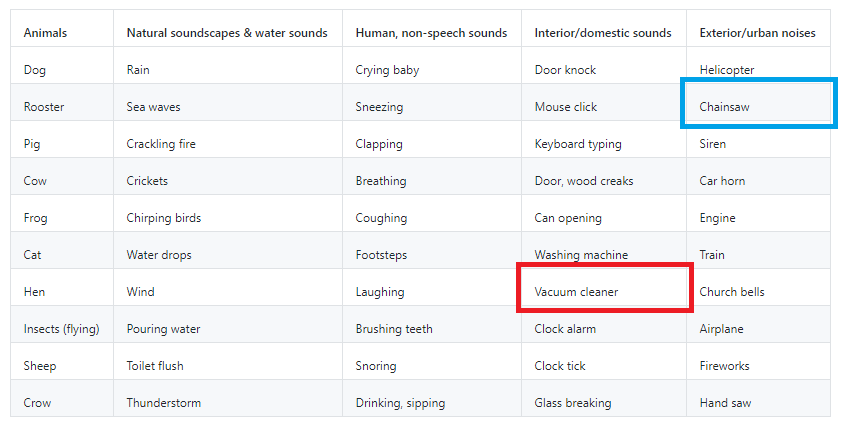
今回は「チェーンソーの音」を正常データ、「掃除機の音」を異常データとして選定しました。
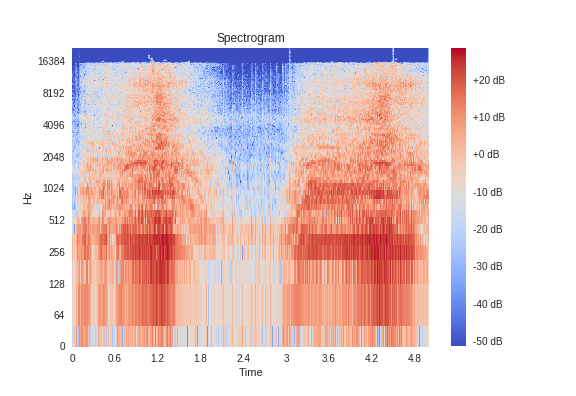
似たようなスペクトログラムですが、掃除機は特定の周波数で強い音を出し、ブレが少ないです。
データの個数
今回もDOCを使って異常検知させます。
DOCの理論は前々回の記事を参考にしてください。
各種のデータの個数は以下のとおりです。
| 個数 | 備考 | |
|---|---|---|
| リファレンスデータ | 2840 | 掃除機とチェーンソー以外 |
| ターゲットデータ | 30 | チェーンソー |
| テストデータ(正常) | 10 | チェーンソー |
| テストデータ(異常) | 40 | 掃除機 |
ただし、リファレンスデータは元データ1920個に対し、Data Augmentationで
2倍に増やしています。音データのData Augmentationについては、以下の記事を
参考にしてください。
https://qiita.com/cvusk/items/61cdbce80785eaf28349#augmentation
テストデータはかなり不均衡ですが、最後にROC曲線で評価するため、不均衡は緩和されます。
データの前処理
今回もDOCにデータを投げますが、その前に、音の生データを周波数データに
変換する必要があります。
選択肢として、スペクトログラムとメルスペクトログラムの二つがあり、今回は
スペクトログラムを採用しました。
その理由はこちらの記事で良い結果が出たからです。
学習済モデルの準備
DOCでは、畳み込みニューラルネットワーク(CNN)の学習済モデルを用意しなければいけません。
ただ、音データの場合、ダウンロードできる学習済モデルがないため、自分で学習させた
モデルを用意する必要があります。以前にこちらで学習用のコードを書いてあったので、
流用します。
ただし、今回はColaboratoryのTPUで学習させるため、コードを一部書き換えています。
X_train,X_test,y_train,y_testを用意して学習してあげてください。
import tensorflow as tf
import tensorflow.keras.backend as K
from tensorflow.keras.layers import Input, Conv2D, GlobalAveragePooling2D, BatchNormalization
from tensorflow.keras.layers import Add, Activation, Dense, Add
from tensorflow.keras.models import Model
from tensorflow.keras.utils import to_categorical
from tensorflow.contrib.tpu.python.tpu import keras_support
from tensorflow.keras.callbacks import ModelCheckpoint
# redefine target data into one hot vector
classes = 50
Y_train = to_categorical(y_train, classes)
Y_test = to_categorical(y_test, classes)
def cba(inputs, filters, kernel_size, strides):
x = Conv2D(filters, kernel_size=kernel_size, strides=strides, padding='same')(inputs)
x = BatchNormalization()(x)
x = Activation("relu")(x)
return x
# define CNN
inputs = Input(shape=(X_train.shape[1:]))
x_1 = cba(inputs, filters=32, kernel_size=(1,8), strides=(1,2))
x_1 = cba(x_1, filters=32, kernel_size=(8,1), strides=(2,1))
x_1 = cba(x_1, filters=64, kernel_size=(1,8), strides=(1,2))
x_1 = cba(x_1, filters=64, kernel_size=(8,1), strides=(2,1))
x_2 = cba(inputs, filters=32, kernel_size=(1,16), strides=(1,2))
x_2 = cba(x_2, filters=32, kernel_size=(16,1), strides=(2,1))
x_2 = cba(x_2, filters=64, kernel_size=(1,16), strides=(1,2))
x_2 = cba(x_2, filters=64, kernel_size=(16,1), strides=(2,1))
x_3 = cba(inputs, filters=32, kernel_size=(1,32), strides=(1,2))
x_3 = cba(x_3, filters=32, kernel_size=(32,1), strides=(2,1))
x_3 = cba(x_3, filters=64, kernel_size=(1,32), strides=(1,2))
x_3 = cba(x_3, filters=64, kernel_size=(32,1), strides=(2,1))
x_4 = cba(inputs, filters=32, kernel_size=(1,64), strides=(1,2))
x_4 = cba(x_4, filters=32, kernel_size=(64,1), strides=(2,1))
x_4 = cba(x_4, filters=64, kernel_size=(1,64), strides=(1,2))
x_4 = cba(x_4, filters=64, kernel_size=(64,1), strides=(2,1))
x = Add()([x_1, x_2, x_3, x_4])
x = cba(x, filters=128, kernel_size=(1,16), strides=(1,2))
x = cba(x, filters=128, kernel_size=(16,1), strides=(2,1))
x = GlobalAveragePooling2D()(x)
x = Dense(classes)(x)
x = Activation("softmax")(x)
model = Model(inputs, x)
# model.summary()
# initiate Adam optimizer
opt = tf.train.AdamOptimizer(learning_rate=0.0001)#, decay=1e-6, amsgrad=True)
model.compile(optimizer=opt, loss="categorical_crossentropy", metrics=["acc"])
# TPU
tpu_grpc_url = "grpc://"+os.environ["COLAB_TPU_ADDR"]
tpu_cluster_resolver = tf.contrib.cluster_resolver.TPUClusterResolver(tpu_grpc_url)
strategy = keras_support.TPUDistributionStrategy(tpu_cluster_resolver)
model = tf.contrib.tpu.keras_to_tpu_model(model, strategy=strategy)
# cnnの学習
hist = model.fit(X_train, Y_train,
validation_data=(X_test,Y_test),
epochs=120,
callbacks=[ ModelCheckpoint('weights.h5', monitor='val_acc',
verbose=1, mode='auto', save_best_only='true')],
verbose=1,
batch_size=20)
学習結果は以下のとおりです。
val_accuracy は**77.86%**となりました。
TPUは、GPUより3倍早く学習できました。ちなみに、120エポックで3時間半くらいです。
学習を飛ばしたい人は、こちらからダウンロードしてください。
kerasで学習させたモデルと重みです。
結果
DOC用の学習コードは付録に記載しました。
分布を眺める
異常検知の性能を見る前に、t-sneで分布を可視化します。
下の図は、テストデータの画像($256\times862\times1$)をそのまま可視化したものです。
チェーンソーと掃除機は、スニーカーとブーツのときほど分離していません。
むしろ、混在していると言った方が適切でしょう。
今回は難しいタスクといえるかもしれません。
続いて、下の図はDOCで学習したCNNを使って、テストデータの出力(128次元)を
t-sneで可視化したものです。
さきほどと違って、分布がかなり分離できました。
DOCによる学習の結果といえるでしょう。
異常検知性能
次にCNNの出力で異常検知させます。異常検知手法は、今回もLOFを使います。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import LocalOutlierFactor
from sklearn import metrics
from sklearn.preprocessing import MinMaxScaler
train = []
for i in range(len(X_t_train)):
train.append(model.predict(X_t_train[i].reshape(1,256,862,1)))
test_s = []
for i in range(len(X_test_normal)):
test_s.append(model.predict(X_test_normal[i].reshape(1,256,862,1)))
test_b = []
for i in range(len(X_test_anomaly)):
test_b.append(model.predict(X_test_anomaly[i].reshape(1,256,862,1)))
train = np.array(train).reshape((len(X_t_train),-1))
test_s = np.array(test_s).reshape((len(X_test_normal),-1))
test_b = np.array(test_b).reshape((len(X_test_anomaly),-1))
ms = MinMaxScaler()
train = ms.fit_transform(train)
test_s = ms.transform(test_s)
test_b = ms.transform(test_b)
# fit the model
clf = LocalOutlierFactor(n_neighbors=5)
y_pred = clf.fit(train)
# plot the level sets of the decision function
Z1 = -clf._decision_function(test_s)
Z2 = -clf._decision_function(test_b)
# ROC曲線の描画
y_true = np.zeros(len(test_s)+len(test_b))
y_true[len(test_s):] = 1#0:正常、1:異常
# FPR, TPR(, しきい値) を算出
fpr, tpr, _ = metrics.roc_curve(y_true, np.hstack((Z1, Z2)))
# AUC
auc = metrics.auc(fpr, tpr)
# ROC曲線をプロット
plt.plot(fpr, tpr, label='DeepOneClassification(AUC = %.2f)'%auc)
plt.legend()
plt.title('ROC curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.grid(True)
plt.show()
今回は一つのファイルが重く、バッチ処理でpredictできないため、一つずつ
処理しています。仮に、バッチ処理するとColaboratoryがメモリーエラーで落ちます。
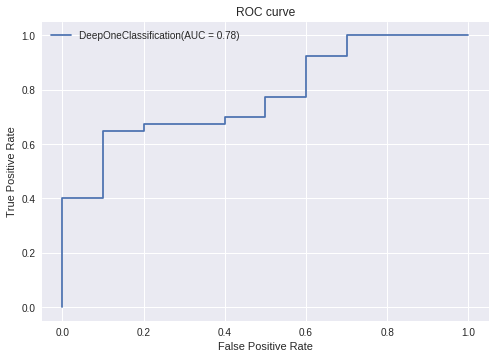
ROC曲線は以下のとおりです。
AUCは0.78となりました。ちなみに、一番良いときの精度は86%ほど出ています。
画像のときと同様にうまく異常検知できています。
実は、別のプロジェクトでこちらの技術を使って、音ファイルで異常検知させると、
AUCは0.53ほどでした。DOCの方が優れた異常検知性能を持っています。
推論時間は一つのファイルで、1.12秒(Colaboratoryで計測)でした。
MobileNetライクな構造にすれば、0.1秒くらいになるとは思いますが、
今回は趣味でやっているので、ここまでとします。仕事で使うシーンが
来たら、改造して記事にしようと思います。
スペクトログラムとスコアの関係
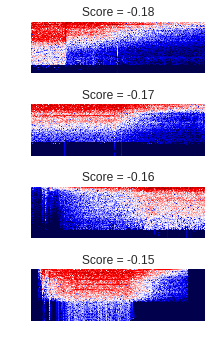
次に、スペクトログラムと異常スコアの関係を見てみましょう。
異常スコアは大きければ大きいほど、チェーンソー(正常音)から外れていると見なします。
最初は、チェーンソー(正常音)のスコアから見てみます。
冒頭で見たとおり、ブレが大きく、時間変化が大きいのが特徴です。
次に、掃除機(異常音)のスコアを見てみます。
下図は、異常スコアが大きかった掃除機、つまりチェーンソーに全然似ていないと
判定された掃除機の音です。
チェーンソーと違って、ブレが小さく、時間変化も小さいです。
最後に、異常スコアが小さかった掃除機、つまりチェーンソーに酷似していると
判定された掃除機の音です。
全体的にブレは小さいものの、時間変化が大きく、チェーンソーに
似ているといえるかもしれません。
まとめ
- DOCは画像のみならず、音の異常検知でも優れた性能を発揮する。
- 今のところ、推論速度は遅いが、ネットワークの構造を改造すれば、ラズパイなどのモバイル端末でも十分に動作する可能性がある。
付録
最後に、DOC学習用のコードを記載します。
from keras.optimizers import Adam, SGD
from keras.models import Model
from keras.layers import GlobalAveragePooling2D, Dense
from keras import backend as K
from keras.engine.network import Network
from keras.models import model_from_json
from keras.utils import to_categorical
# redefine target data into one hot vector
classes = 50
Y_train = to_categorical(y_train, classes)
Y_test = to_categorical(y_test, classes)
freq = 256
time = 862
input_shape = (freq, time, 1)
batchsize = 20
feature_out = 128 #secondary network out
lambda_ = 0.1 #for compact loss
# 損失関数
def original_loss(y_true, y_pred):
lc = 1/(classes*batchsize) * batchsize**2 * K.sum((y_pred -K.mean(y_pred,axis=0))**2,axis=[1]) / ((batchsize-1)**2)
return lc
# 学習
def train(x_target, x_ref, y_ref, epoch_num):
# 学習済モデル読み込み, S network用
model = model_from_json(open('model.json').read())
model.load_weights('weights.h5')
#最終層削除
model.layers.pop()
model.layers.pop()
# 重みを固定
for layer in model.layers:
if layer.name == "conv2d_17 (Conv2D)":
break
else:
layer.trainable = False
model_t = Model(inputs=model.input, outputs=model.layers[-1].output)
# R network用 Sと重み共有
model_r = Network(inputs=model_t.input,
outputs=model_t.output,
name="shared_layer")
#Rに全結合層を付ける
prediction = Dense(classes, activation='softmax')(model_t.output)
model_r = Model(inputs=model_r.input,outputs=prediction)
#コンパイル
optimizer = SGD(lr=5e-5, decay=0.00005)
model_r.compile(optimizer=optimizer, loss="categorical_crossentropy")
model_t.compile(optimizer=optimizer, loss=original_loss)
#model_t.summary()
#model_r.summary()
print("x_target is",x_target.shape[0],'samples')
print("x_ref is",x_ref.shape[0],'samples')
ref_samples = np.arange(x_ref.shape[0])
loss, loss_c = [], []
print("training...")
for epochnumber in range(epoch_num):
x_r, y_r, lc, ld = [], [], [], []
#データシャッフル
np.random.shuffle(x_target)
np.random.shuffle(ref_samples)
for i in range(len(x_target)):
x_r.append(x_ref[ref_samples[i]])
y_r.append(y_ref[ref_samples[i]])
x_r = np.array(x_r)
y_r = np.array(y_r)
for i in range(int(len(x_target) / batchsize)):
#batchsize分のデータロード
batch_target = x_target[i*batchsize:i*batchsize+batchsize]
batch_ref = x_r[i*batchsize:i*batchsize+batchsize]
batch_y = y_r[i*batchsize:i*batchsize+batchsize]
#target data
#学習しながら、損失を取得
lc.append(model_t.train_on_batch(batch_target, np.zeros((batchsize, feature_out))))
#reference data
#学習しながら、損失を取得
ld.append(model_r.train_on_batch(batch_ref, batch_y))
loss.append(np.mean(ld))
loss_c.append(np.mean(lc))
if (epochnumber+1) % 1 == 0:
print("epoch:",epochnumber+1)
print("Descriptive loss:", loss[-1])
print("Compact loss", loss_c[-1])
#結果グラフ
plt.plot(loss,label="Descriptive loss")
plt.xlabel("epoch")
plt.legend()
plt.show()
plt.plot(loss_c,label="Compact loss")
plt.xlabel("epoch")
plt.legend()
plt.show()
return model_t
model = train(X_t_train, X_train, Y_train, 5)