はじめに
ふと思い立って勉強を始めた「ゼロから作るDeep Learning❷ーー自然言語処理編」の4章で私がつまずいたことのメモです。
実行環境はmacOS Catalina + Anaconda 2019.10、Pythonのバージョンは3.7.4です。詳細はこのメモの1章をご参照ください。
(このメモの他の章へ:1章 / 2章 / 3章 / 4章 / 5章 / 6章 / 7章 / 8章 / まとめ)
この記事は個人で作成したものであり、内容や意見は所属企業・部門見解を代表するものではありません。
4章 word2vecの高速化
この章は、3章で作ったword2vecのCBOWモデルの高速化です。
4.1 word2vecの改良①
まず入力層から中間層までの高速化です。この部分は単語を分散表現に変換する埋め込みの役割を担いますが、MatMulレイヤーだと無駄が多いのでEmbeddingレイヤーへ置き換えます。
Embeddingレイヤーはシンプルなのですが、逆伝播の実装でidxが重複している場合に $ dW $ を加算する部分が少し分かりにくいかも知れません。本では図4-5で取り上げられていて、「なぜ加算を行うかは、各自で考えてみましょう」と解説が省略されています。
そこで、MatMulレイヤーの時の逆伝播の計算と比較することで考えてみました。EmbeddingレイヤーはMatMulレイヤーと同じ結果にならないといけないためです。
まず、図4-5における $ idx $ をMatMulレイヤーにおける $ x $ に戻します。
\begin{align}
idx &=
\begin{pmatrix}
0\\
2\\
0\\
4\\
\end{pmatrix}\\
\\
x &=
\begin{pmatrix}
1 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 1 & 0 & 0 & 0 & 0\\
1 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 1 & 0 & 0\\
\end{pmatrix}
\end{align}
MatMulレイヤーの逆伝播の式は $ \frac{\partial L}{\partial W} = x^T\frac{\partial L}{\partial y} $ (P.33参照)なので、図4-5の表記に置き換えると $ dw = x^Tdh $ になります。ここに $ x $ と図4-5の $ dh $ を当てはめて$ dW $を計算すると次のようになります。なお、本当は $dh$ を図4-5の通りにしたかったのですが本のように●の濃淡を表現できないので、ここでは $ ●、◆、a、b $ で表現しています。
\begin{align}
dW &= x^Tdh\\
\\
\begin{pmatrix}
? & ? & ? \\
○ & ○ & ○ \\
●_1 & ●_2 & ●_3 \\
○ & ○ & ○ \\
◆_1 & ◆_2 & ◆_3 \\
○ & ○ & ○ \\
○ & ○ & ○ \\
\end{pmatrix}
&=
\begin{pmatrix}
1 & 0 & 1 & 0\\
0 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
\end{pmatrix}
\begin{pmatrix}
a_1 & a_2 & a_3 \\
●_1 & ●_2 & ●_3 \\
b_1 & b_2 & b_3 \\
◆_1 & ◆_2 & ◆_3 \\
\end{pmatrix}\\
\end{align}
計算すると分かりますが、$ dh $ の2行目( $ ●_1 ●_2 ●_3 $)と4行目( $ ◆_1 ◆_2 ◆_3 $)は、図4-5のようにそのまま $ dW $ の3行目と5行目になります。そして、問題になっている $ dW $ の1行目の $ ? $ は、次のようになります。
\begin{align}
\begin{pmatrix}
a_1 + b_1 & a_2 + b_2 & a_3 + b_3 \\
○ & ○ & ○ \\
●_1 & ●_2 & ●_3 \\
○ & ○ & ○ \\
◆_1 & ◆_2 & ◆_3 \\
○ & ○ & ○ \\
○ & ○ & ○ \\
\end{pmatrix}
&=
\begin{pmatrix}
1 & 0 & 1 & 0\\
0 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 1\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
\end{pmatrix}
\begin{pmatrix}
a_1 & a_2 & a_3 \\
●_1 & ●_2 & ●_3 \\
b_1 & b_2 & b_3 \\
◆_1 & ◆_2 & ◆_3 \\
\end{pmatrix}
\end{align}
つまり、$ dh $ の1行目と3行目を加算していることが分かります。このMatMulレイヤーの計算と同じことをEmbeddingレイヤーでも実装しないといけないので、加算する必要があるという訳です。
4.2 word2vecの改良②
続いて中間層から出力層への改良です。負例を使った学習を大胆に削減してしまおうというNegative Samplingのアイデアは面白いですね。
大きくつまずく点はなかったのですが、本ではEmbedding Dotレイヤーの逆伝播の解説が「難しい問題ではないので、各自で考えてみましょう」ということで省略されているので、ここを少しまとめてみます。
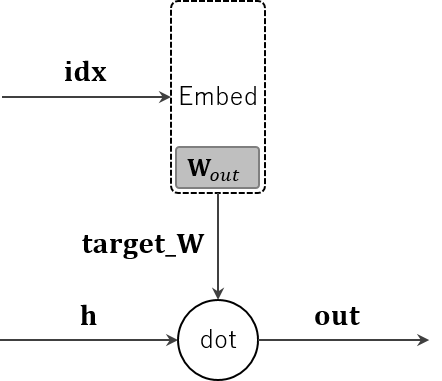
図4-12の中で、Embedding Dotレイヤーの部分だけ切り出すと次のようになります。
dotノードでやっていることは各要素ごとの乗算と、それらの結果の加算です。そのため、乗算ノード(1章の「1.3.4.1 乗算ノード」参照)とSumノード(1章の「1.3.4.4 Sumノード」参照)に分解して逆伝播を考えます。そうすると次の形になります。青字が逆伝播です。
これを1つ前のDotノードの図に戻すと、次の形になります。
この図の通りに実装すればOKですが、そのままでは dout の形状が h や target_W と合わないので、NumPyの * で要素ごとの積が求められません。そのため最初に dout.reshape(dout.shape[0], 1) で形状を合わせてから積を求めます。この流れで実装すると、本の EmbeddingDot.backwad() のコードになることがわかるかと思います。
4.3 改良版word2vecの学習
学習の実装は特につまずくところはありません。本ではPTBコーパスを使っていますが、やっぱり日本語が好きなので、2章同様に青空文庫の分かち書き済みテキストで学習してみました。
コーパスの取得はdataset/ptb.pyの代わりに改造版のdataset/aozorabunko.pyを使います。このソースや仕組みなどについては、2章のメモの「カウントベースの手法の改善」のところに書いていますので、そちらをご参照ください。
ch04/train.pyも、以下のように青空文庫のコーパスを使うように変更しています。コメントに★のあるのが変更箇所です。
# coding: utf-8
import sys
sys.path.append('..')
from common import config
# GPUで実行する場合は、下記のコメントアウトを消去(要cupy)
# ===============================================
# config.GPU = True
# ===============================================
from common.np import *
import pickle
from common.trainer import Trainer
from common.optimizer import Adam
from cbow import CBOW
from skip_gram import SkipGram
from common.util import create_contexts_target, to_cpu, to_gpu
from dataset import aozorabunko # ★青空文庫のコーパスを利用するように変更
# ハイパーパラメータの設定
window_size = 5
hidden_size = 100
batch_size = 100
max_epoch = 10
# データの読み込み
corpus, word_to_id, id_to_word = aozorabunko.load_data('train') # ★コーパス変更
vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
if config.GPU:
contexts, target = to_gpu(contexts), to_gpu(target)
# モデルなどの生成
model = CBOW(vocab_size, hidden_size, window_size, corpus)
# model = SkipGram(vocab_size, hidden_size, window_size, corpus)
optimizer = Adam()
trainer = Trainer(model, optimizer)
# 学習開始
trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()
# 後ほど利用できるように、必要なデータを保存
word_vecs = model.word_vecs
if config.GPU:
word_vecs = to_cpu(word_vecs)
params = {}
params['word_vecs'] = word_vecs.astype(np.float16)
params['word_to_id'] = word_to_id
params['id_to_word'] = id_to_word
pkl_file = 'cbow_params.pkl' # or 'skipgram_params.pkl'
with open(pkl_file, 'wb') as f:
pickle.dump(params, f, -1)
なお、手元の環境では学習に8時間くらいかかりました。
続いて結果の確認です。標準入力からいろいろな言葉を試せるように、ch04/eval.pyを少し変えました。★が変更箇所です。
# coding: utf-8
import sys
sys.path.append('..')
from common.util import most_similar, analogy
import pickle
pkl_file = 'cbow_params.pkl'
# pkl_file = 'skipgram_params.pkl'
with open(pkl_file, 'rb') as f:
params = pickle.load(f)
word_vecs = params['word_vecs']
word_to_id = params['word_to_id']
id_to_word = params['id_to_word']
# most similar task ★クエリを標準入力する形に変更
while True:
query = input('\n[similar] query? ')
if not query:
break
most_similar(query, word_to_id, id_to_word, word_vecs, top=5)
# analogy task ★クエリを標準入力する形に変更
print('-'*50)
while True:
query = input('\n[analogy] query? (3 words) ')
if not query:
break
a, b, c = query.split()
analogy(a, b, c, word_to_id, id_to_word, word_vecs)
以下、いろいろ試してみた結果です。
まず類似単語の確認です。比較のために2章で試したカウントベースのものも記載ました。また、CBOWのウィンドウサイズが本のコードでは5でしたが、カウントベースの時と同じ2も試してみました。
| 類似単語 | 2章のカウントベース (ウィンドウサイズ:2) |
CBOW (ウィンドウサイズ:5) |
CBOW (ウィンドウサイズ:2) |
|---|---|---|---|
| あなた | 奥さん: 0.6728986501693726 妻: 0.6299399137496948 K: 0.6205178499221802 父: 0.5986840128898621 私: 0.5941839814186096 |
お前: 0.7080078125 奥さん: 0.6748046875 妻: 0.64990234375 お嬢さん: 0.63330078125 あたし: 0.62646484375 |
奥さん: 0.7373046875 お前: 0.7236328125 妻: 0.68505859375 本人: 0.677734375 先生: 0.666015625 |
| 年 | 反: 0.8162745237350464 百: 0.8051895499229431 分: 0.7906433939933777 八: 0.7857747077941895 円: 0.7682645320892334 |
円: 0.78515625 分: 0.7744140625 年間: 0.720703125 世紀: 0.70751953125 時半: 0.70361328125 |
坪: 0.71923828125 メートル: 0.70947265625 分: 0.7080078125 分の: 0.7060546875 秒: 0.69091796875 |
| 車 | ドア: 0.6294019222259521 ドアー: 0.6016885638237 自動車: 0.5859153270721436 門: 0.5726617574691772 カーテン: 0.5608214139938354 |
上半身: 0.74658203125 蔵: 0.744140625 洋館: 0.7353515625 階段: 0.7216796875 ドア: 0.71484375 |
階段: 0.72216796875 自動車: 0.7216796875 洞窟: 0.716796875 地下: 0.7138671875 扉: 0.71142578125 |
| トヨタ | トヨタ is not found | トヨタ is not found | トヨタ is not found |
| 朝 | 晩: 0.7267987132072449 ごろ: 0.660172164440155 昼: 0.6085118055343628 夕方: 0.6021789908409119 翌: 0.6002975106239319 |
夕方: 0.65576171875 国元: 0.65576171875 最初: 0.65087890625 天長節: 0.6494140625 次: 0.64501953125 |
夕方: 0.68115234375 昼: 0.66796875 ゆうべ: 0.6640625 晩: 0.64453125 門内: 0.61376953125 |
| 学校 | 東京: 0.6504884958267212 高等: 0.6290650367736816 中学校: 0.5801640748977661 大学: 0.5742003917694092 下宿: 0.5358142852783203 |
大学: 0.81201171875 下宿: 0.732421875 住田: 0.7275390625 生徒: 0.68212890625 中学校: 0.6767578125 |
中学: 0.69677734375 大学: 0.68701171875 近頃: 0.6611328125 東京: 0.65869140625 ここ: 0.65771484375 |
| 座敷 | 書斎: 0.6603355407714844 椽側: 0.6362787485122681 室: 0.6142982244491577 部屋: 0.6024710536003113 台所: 0.6014574766159058 |
床: 0.77685546875 机: 0.76513671875 敷居: 0.76513671875 本堂: 0.744140625 玄関: 0.73681640625 |
机: 0.69970703125 床: 0.68603515625 椽: 0.6796875 書斎: 0.6748046875 雑司ヶ谷: 0.6708984375 |
| 着物 | 髯: 0.5216895937919617 黒: 0.5200990438461304 服: 0.5096032619476318 洋服: 0.48781922459602356 帽子: 0.4869200587272644 |
避け: 0.68896484375 冷汗: 0.6875 醒す: 0.67138671875 襯衣: 0.6708984375 とどのつまり: 0.662109375 |
装束: 0.68359375 見世: 0.68212890625 綿: 0.6787109375 奏する: 0.66259765625 硯: 0.65966796875 |
| 吾輩 | 主人: 0.6372452974319458 余: 0.5826579332351685 金田: 0.4684762954711914 彼等: 0.4676626920700073 迷亭: 0.4615904688835144 |
主人: 0.7861328125 彼等: 0.7490234375 余: 0.71923828125 猫: 0.71728515625 やむを得ない: 0.69287109375 |
主人: 0.80517578125 彼等: 0.6982421875 猫: 0.6962890625 細君: 0.6923828125 レッシング: 0.6611328125 |
| 犯人 | 怪人: 0.6609077453613281 賊: 0.6374931931495667 団員: 0.6308270692825317 あいつ: 0.6046633720397949 潜航: 0.5931873917579651 |
こんど: 0.7841796875 首領: 0.75439453125 あいつ: 0.74462890625 宝石: 0.74169921875 わし: 0.73779296875 |
魚つり: 0.77392578125 あいつ: 0.74072265625 近日: 0.7392578125 軽気球: 0.7021484375 難症: 0.70166015625 |
| 注文 | 話: 0.6200630068778992 相談: 0.5290789604187012 多忙: 0.5178924202919006 親切: 0.5033778548240662 講釈: 0.4894390106201172 |
催促: 0.6279296875 鑑定: 0.61279296875 卒業: 0.611328125 総会: 0.6103515625 贅沢: 0.607421875 |
相談: 0.65087890625 忠告: 0.63330078125 鑑定: 0.62451171875 辞儀: 0.61474609375 発議: 0.61474609375 |
| 無鉄砲 | 陳腐: 0.7266454696655273 古風: 0.6771457195281982 鋸: 0.6735808849334717 鼻息: 0.6516652703285217 無知: 0.650424063205719 |
信条: 0.7353515625 上分別: 0.7294921875 主役: 0.693359375 産まれ: 0.68603515625 受売: 0.68603515625 |
立場: 0.724609375 手近: 0.71630859375 路次: 0.71142578125 貌: 0.70458984375 演題: 0.69921875 |
| 猫 | 南無: 0.6659030318260193 信女: 0.5759447813034058 墨: 0.5374482870101929 身分: 0.5352671146392822 普通: 0.5205280780792236 |
智識: 0.728515625 吾輩: 0.71728515625 画: 0.70751953125 胃弱: 0.67431640625 食意地: 0.66796875 |
吾輩: 0.6962890625 中学: 0.6513671875 恋: 0.64306640625 彼等: 0.63818359375 豚: 0.6357421875 |
| 酒 | 書物: 0.5834404230117798 茶: 0.469807893037796 休ん: 0.4605821967124939 食う: 0.44864168763160706 棒: 0.4349029064178467 |
飲ん: 0.6728515625 喧嘩: 0.6689453125 飯: 0.66259765625 山越: 0.646484375 蕎麦: 0.64599609375 |
ヴァイオリン: 0.63232421875 月給: 0.630859375 薬: 0.59521484375 手榴弾: 0.59521484375 綺羅: 0.5947265625 |
| 料理 | かせぎ: 0.5380040407180786 落款: 0.5214874744415283 原: 0.5175281763076782 法: 0.5082278847694397 屋: 0.5001937747001648 |
館: 0.68896484375 史: 0.615234375 小説: 0.59912109375 文芸: 0.5947265625 採る: 0.59033203125 |
雑誌: 0.666015625 小間物: 0.65625 鍛冶: 0.61376953125 音楽: 0.6123046875 呉服: 0.6083984375 |
2章の時と変わらず、なかなかの混乱ぶりです。とても優劣は付けられません。「我輩」で「猫」とか出てきてしまう辺りがコーパスの偏りを示していますね。夏目漱石、宮沢賢治、江戸川乱歩の3名の作品しか使っていないのと、コーパスのサイズが小さすぎることが原因だと思われます。
続いて類推問題です。
| 類推問題 | CBOW(ウィンドウサイズ:5) | CBOW(ウィンドウサイズ:2) |
|---|---|---|
| 男:王 = 女:? | ぬ: 5.25390625 ない: 4.2890625 ず: 4.21875 るる: 3.98828125 糞: 3.845703125 |
大鳥: 3.4375 一刻: 3.052734375 裏門: 2.9140625 かげ: 2.912109375 床柱: 2.873046875 |
| 体:顔 = 自動車:? | 警官: 6.5 ドア: 5.83984375 ふたり: 5.5625 警部: 5.53515625 係長: 5.4765625 |
ドア: 3.85546875 穴: 3.646484375 電灯: 3.640625 警部: 3.638671875 肩: 3.6328125 |
| 行く:来る = 話す:? | 言う: 4.6640625 十一: 4.546875 十三: 4.51171875 聞く: 4.25 尋ねる: 4.16796875 |
聞く: 4.3359375 惜しい: 4.14453125 宮: 4.11328125 いう: 3.671875 十一: 3.55078125 |
| 飯:食う = 書物:? | 有し: 4.3671875 求める: 4.19140625 人望: 4.1328125 山路: 4.06640625 受ける: 3.857421875 |
促: 3.51171875 碌: 3.357421875 いう: 3.2265625 聞く: 3.2265625 ぬすみだす: 3.17578125 |
| 夏:暑い = 冬:? | たまる: 5.23828125 てる: 4.171875 くる: 4.10546875 いたる: 4.05859375 いく: 3.978515625 |
十一: 4.29296875 済ん: 3.853515625 十三: 3.771484375 なる: 3.66015625 わるい: 3.66015625 |
いきなり最初の問題で、低いスコアながらも困った結果が混ざっています。学習データが不十分だと怖いことが起きますね。昨今の「説明可能なAI」が求められる背景を垣間見た感じがします。
他の結果もボロボロですが、かろうじて「体:顔 = 自動車:?」や「行く:来る = 話す:?」には正解も混ざっていました。「自動車」で「警官」や「警部」が出てくるのは江戸川乱歩の影響でしょう。
やっぱり素直にWikipediaの日本語版を使うべきだったかも知れませんが、天邪鬼なもので![]() なお、Wikipediaを試している方はたくさんいるので、興味のある方は「wikipedia 日本語 コーパス」などでググってみてください。
なお、Wikipediaを試している方はたくさんいるので、興味のある方は「wikipedia 日本語 コーパス」などでググってみてください。
4.4 word2vecに関する残りのテーマ
転移学習の例としてメールのネガポジ判定が解説されていますが、この章までの知識では単語を固定長のベクトルに変換できても、メールのような文章を固定長のベクトルに変換することはできません。そのため、まだこのようなタスクには挑戦できません。
あと、分散表現の質に関して、日本語の場合は事前の分かち書きの質も大きく影響しそうです。日本語の分散表現モデルがいくつか公開されていますが、それらを転移学習することを考えた場合、同じ分かち書きの仕組み(ロジックや辞書の内容、パラメーターなど)を使うことが前提になるかと思います。そうなると、例えば業界や個社特有の専門用語などを扱うタスクでは、簡単には転移学習できないということになるのでしょうか。日本語はいろいろ大変な感じです。
4.5 まとめ
やっとこの本の前半が終わりましたが、1章は前巻のおさらいだったことを考えると、まだまだ1/3くらいかも知れません。先は長そうです……
この章は以上です。誤りなどありましたら、ご指摘いただけますとうれしいです。