時系列データ解析の為にRNNを使ってみようと思い,簡単な実装をして,時系列データとして
ほとんど,以下の真似ごとなのでいいねはそちらにお願いします.
深層学習ライブラリKerasでRNNを使ってsin波予測
LSTM で正弦波を予測する
CHANGE LOG
2020/07/12
- Sequenceの長さを25 → 50で再学習させた場合を追記
- ライブラリをスタンドアロンKeras → Tensorflow.kerasに変更
ライブラリ
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Activation
from tensorflow.keras.layers import LSTM
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.callbacks import EarlyStopping
import numpy as np
import matplotlib.pyplot as plt
今回はLSTMを構築するため,recurrentからLSTMをimportする
また,学習時間などのリソースを節約するためにEarlyStoppingもimportしている.
データの作成
Sin波の生成
はじめに,sin波を生成する.
def sin(x, T=100):
return np.sin(2.0 * np.pi * x / T)
# sin波にノイズを付与する
def toy_problem(T=100, ampl=0.05):
x = np.arange(0, 2 * T + 1)
noise = ampl * np.random.uniform(low=-1.0, high=1.0, size=len(x))
return sin(x) + noise
f = toy_problem()
Sin波をRNNに通すための形に成型
以下のように学習データとして25ステップ分につきとラベルデータを1つで1つの学習データを表現する.
def make_dataset(low_data, n_prev=100):
data, target = [], []
maxlen = 25
for i in range(len(low_data)-maxlen):
data.append(low_data[i:i + maxlen])
target.append(low_data[i + maxlen])
re_data = np.array(data).reshape(len(data), maxlen, 1)
re_target = np.array(target).reshape(len(data), 1)
return re_data, re_target
# g -> 学習データ,h -> 学習ラベル
g, h = make_dataset(f)
モデルの生成
簡単なLSTMの学習モデルを作成する.LSTMの概念は,以下が非常に分かり易いです.
LSTMネットワークの概要
# モデル構築
# 1つの学習データのStep数(今回は25)
length_of_sequence = g.shape[1]
in_out_neurons = 1
n_hidden = 300
model = Sequential()
model.add(LSTM(n_hidden, batch_input_shape=(None, length_of_sequence, in_out_neurons), return_sequences=False))
model.add(Dense(in_out_neurons))
model.add(Activation("linear"))
optimizer = Adam(lr=0.001)
model.compile(loss="mean_squared_error", optimizer=optimizer)
- n_hidden: 隠れ層 -> 数が多い程,学習モデルの複雑さが増加
- batch_input_shape: LSTMに入力するデータの形を指定([バッチサイズ,step数,特徴の次元数]を指定する)
- Denseでニューロンの数を調節しているだけ.今回は,時間tにおけるsin波のy軸の値が出力なので,ノード数1にする.
- 線形の活性化関数を用いている.
- compileで,誤差関数:最小2乗誤差,最適化手法: Adamを用いるように定義
学習
生成した学習データ,定義したモデルを用いて,学習を行う.
今回は,学習データの10%をvalidationに用いて,100 epochで学習させた.
1行目のearly_stoppingをcallbacksで定義することで,validationの誤差値(val_loss)の変化が収束したと判定された場合に自動で学習を終了する.modeをautoにすることで,収束の判定を自動で行う.
patienceは,判定値からpatienceの値の分だけのepochは学習して,変化がなければ終了するように判定する.なので,patience=0だと,val_lossが上昇した瞬間,学習が終了することになる.
early_stopping = EarlyStopping(monitor='val_loss', mode='auto', patience=20)
model.fit(g, h,
batch_size=300,
epochs=100,
validation_split=0.1,
callbacks=[early_stopping]
)
予測
学習データで予測
学習データを予測して,sin波が再現できるか確認.
# 予測
predicted = model.predict(g)
これで,predictedにt=25以降のsin波を予測させることができる.
実際にplotしてみる.
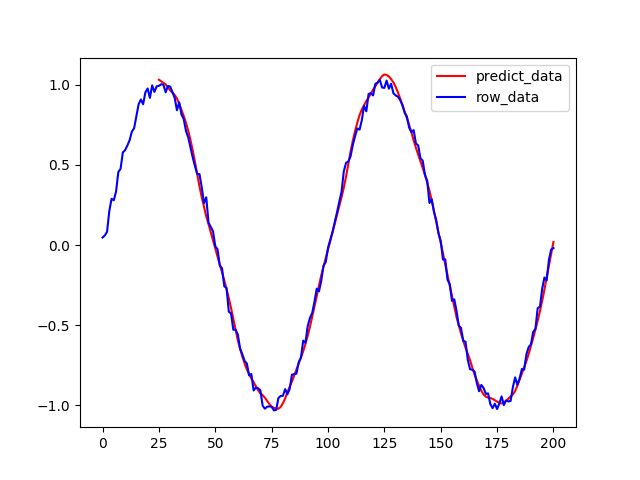
plt.figure()
plt.plot(range(25,len(predicted)+25),predicted, color="r", label="predict_data")
plt.plot(range(0, len(f)), f, color="b", label="row_data")
plt.legend()
plt.show()
予測sin波の方は,ほとんどノイズの影響を受けずに予測することができている.
未来の予測
生成した学習モデルを用いて,学習データ以降の時間のsin波の座標を予測する.
# 1つの学習データの時間の長さ -> 25
time_length = future_test.shape[1]
# 未来の予測データを保存していく変数
future_result = np.empty((1))
# 未来予想
for step2 in range(400):
test_data = np.reshape(future_test, (1, time_length, 1))
batch_predict = model.predict(test_data)
future_test = np.delete(future_test, 0)
future_test = np.append(future_test, batch_predict)
future_result = np.append(future_result, batch_predict)
# sin波をプロット
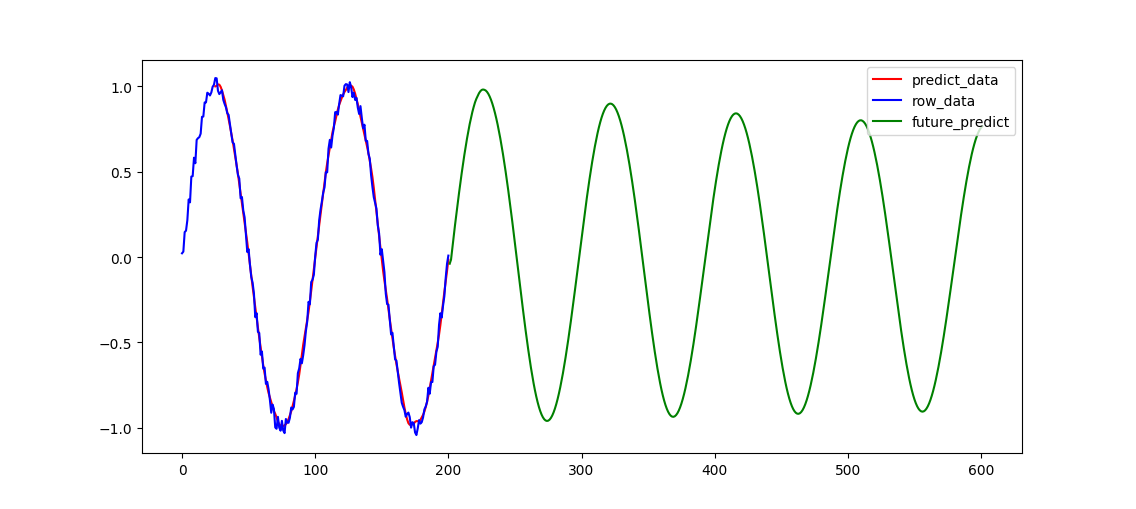
plt.figure()
plt.plot(range(25,len(predicted)+25),predicted, color="r", label="predict_data")
plt.plot(range(0, len(f)), f, color="b", label="row_data")
plt.plot(range(0+len(f), len(future_result)+len(f)), future_result, color="g", label="future_predict")
plt.legend()
plt.show()
少しずつ,振幅が小さくなってしまった・・・
おそらく,1つの学習データの長さが25stepでは,短いのでは??
追記: LSTMの学習を倍の長さでしてみる
25stepでは,足りなかったので,倍の50ステップで学習するとどうなるのか??
データの準備
# 300周期 (601サンプル)にデータに拡張
ex_function = toy_problem(T=300)
# 50サンプルごとに分割
ex_data, ex_label = make_dataset(ex_function, maxlen=50)
あとは,前と同じように,モデルの定義をして,学習をする
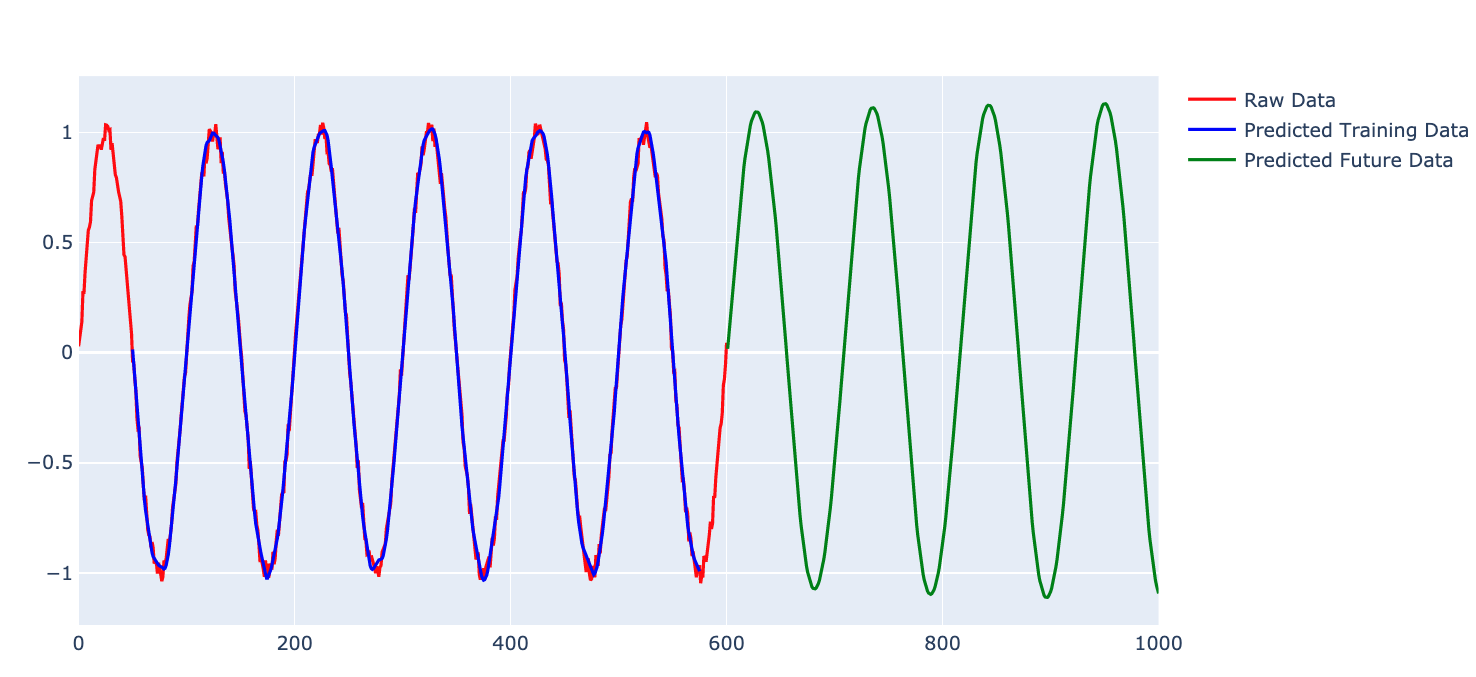
予測結果
Step数を増加させると,誤差の幅が抑制されているようです.
Future Works
誤差の範囲が抑制されたが,LSTMでは限界がある...
Recurrent系のネットワークでは,単純な数値データの予測に向かない(Recurrent系がNLP用に開発されたため) という情報もあるので,今度CNNとの評価をしてみようと思います.
追記
1D-CNNで,同じタスクをやってみました!!
https://qiita.com/sasayabaku/items/2f96a0bee2f8ae098284
Source Code