Motivation
LSTM等のReccurent系のネットワークは,時系列データを予測するのに向いているのですが,
1次元のCNN (1D-CNN)も,1*N ピクセルの画像を予測することなんてほとんどないので,用途のほとんどが時系列のデータになると思います.
なので,どっちが良いのか時系列データの簡単な例 Sin波 で簡単に調べてみようと思います.
Jupyter Notebook
ここに,コードはここにUPしてます.
データの作成
はじめに,Sin波を作成します.
def sin(x, T=100):
return np.sin(2.0 * np.pi * x / T)
# sin波にノイズを付与する
def toy_problem(T=100, ampl=0.05):
x = np.arange(0, 2 * T + 1)
noise = ampl * np.random.uniform(low=-1.0, high=1.0, size=len(x))
return sin(x) + noise
function = toy_problem(T=300)
Sin波をRNNに通すための形に整形
以下のように学習データとして,学習データ: 50ステップ + 予測ラベル: 1ステップ分を1サンプルとして生成します.
注意 : 図は,学習データ: 25ステップになります.
def make_dataset(raw_data, n_prev=100, maxlen=25):
data, target = [], []
for i in range(len(raw_data) - maxlen):
data.append(raw_data[i:i+maxlen])
target.append(raw_data[i+maxlen])
reshaped_data = np.array(data).reshape(len(data), maxlen, 1)
reshaped_target = np.array(target).reshape(len(target), 1)
return reshaped_data, reshaped_target
data, label = make_dataset(f, maxlen=50)
モデルの作成
モデル定義
モデルの構造は結構適当に決めてます.
inputs = Input(shape=(50, 1))
x = Conv1D(30, 2, padding='same', activation='relu')(inputs)
x = MaxPool1D(pool_size=2, padding='same')(x)
x = Conv1D(10, 2, padding='same', activation='relu')(x)
x = MaxPool1D(pool_size=2, padding='same')(x)
x = Flatten()(x)
x = Dense(300, activation='relu')(x)
x = Dense(1, activation='tanh')(x)
model = Model(inputs, outputs=x)
optimizer = Adam(lr=1e-3)
model.compile(loss="mean_squared_error", optimizer=optimizer)
Early Stopping 設定
Validation Lossが,10epoch 下がらなかったら学習を止めます.
early_stopping = callbacks.EarlyStopping(monitor='val_loss', mode='min', patience=10)
学習
学習します.
model.fit(data, label,
batch_size=64, epochs=1000,
validation_split=0.2, callbacks=[early_stopping]
)
予測
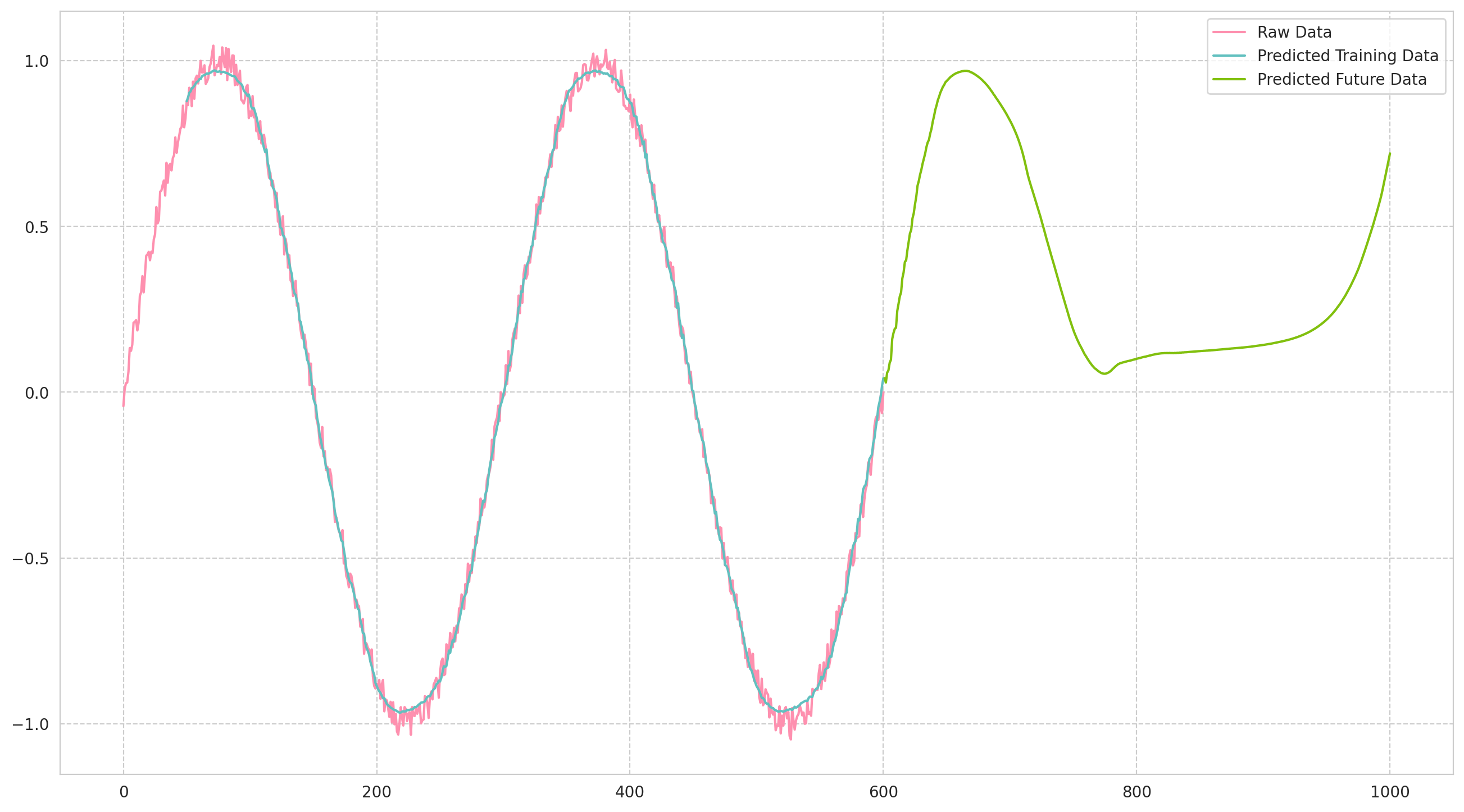
学習データ
まず,学習データに対応できるかを予測します.
predicted = model.predict(data)
将来の予測
学習データの,末尾50ステップで,学習データの後を予測します.
本来は,予測に用いるデータ(=モデルに投入されるデータ)は正しいデータでないといけないのですが,
今回のやり方だと,予測値に誤差があるので,だんだんと予測に用いるデータが誤差を含み出すので,
感覚的に段々とSin波から予測がずれていくのかなと思っています.
- future_test: 未来の1点を予測するための,直近50ステップの時系列データ
- time_length : モデルに投入する時系列データの長さ
- future_result: モデルの予測点を記録する配列
future_test = data[-1].T
time_length = future_test.shape[1]
future_result = np.empty((0))
将来 400点の予測をしてみる
for step in range(400):
test_data = np.reshape(future_test, (1, time_length, 1))
batch_predict = model.predict(test_data)
future_test = np.delete(future_test, 0)
future_test = np.append(future_test, batch_predict)
future_result = np.append(future_result, batch_predict)
結果のグラフ
プロットするコード
fig = plt.figure(figsize=(16, 9), dpi=200)
sns.lineplot(
color="#fe90af",
data=function,
label="Raw Data"
)
sns.lineplot(
color="#61c0bf",
x=np.arange(50, len(predicted)+50),
y=predicted.reshape(-1),
label="Predicted Training Data"
)
sns.lineplot(
color="#81c00e",
x=np.arange(0+len(function), len(function)+len(future_result)),
y=future_result.reshape(-1),
label="Predicted Future Data"
)
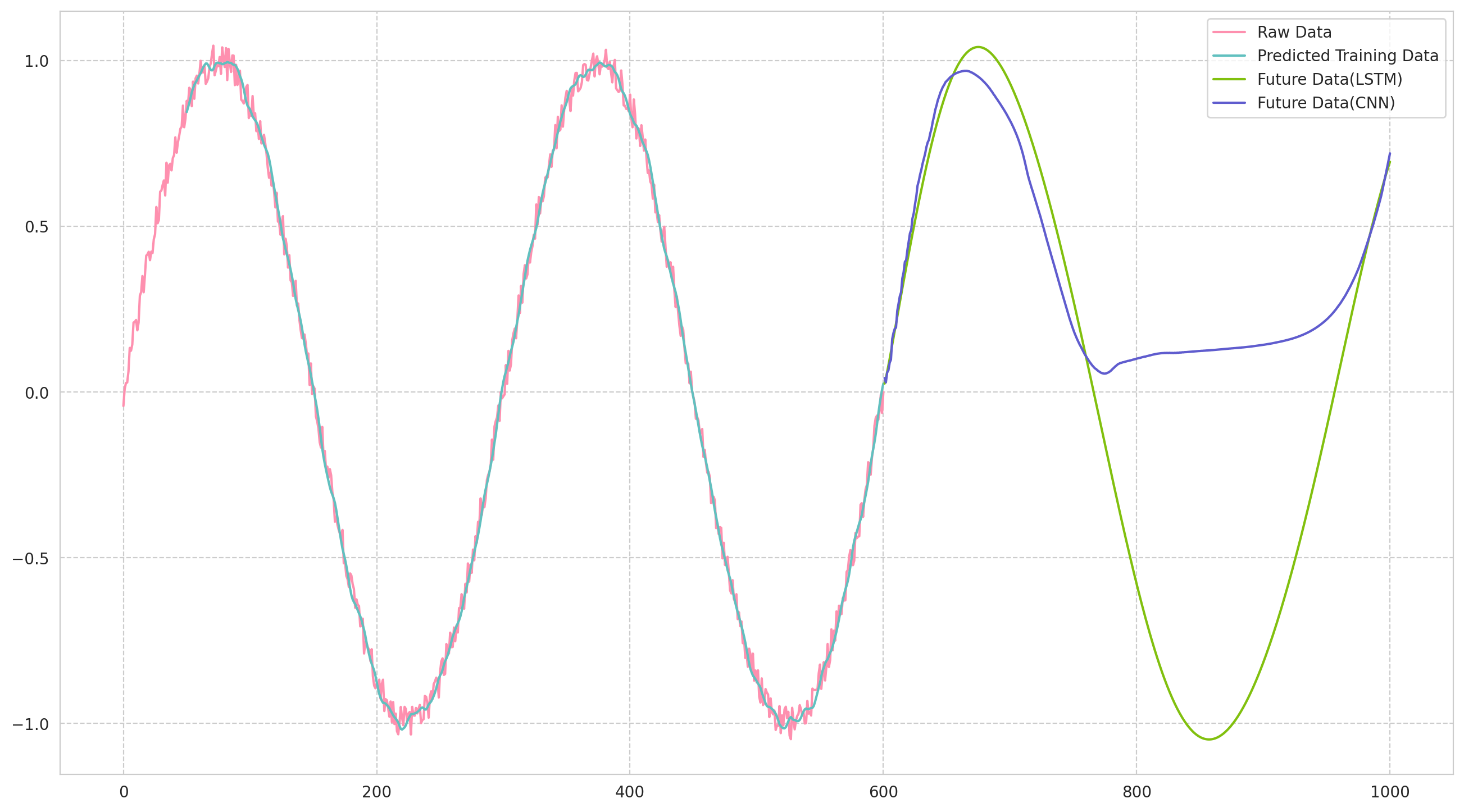
LSTMを比べてみる
LSTMで同じデータを予測した時がこちら.
LSTMは安定して,予測できますね...
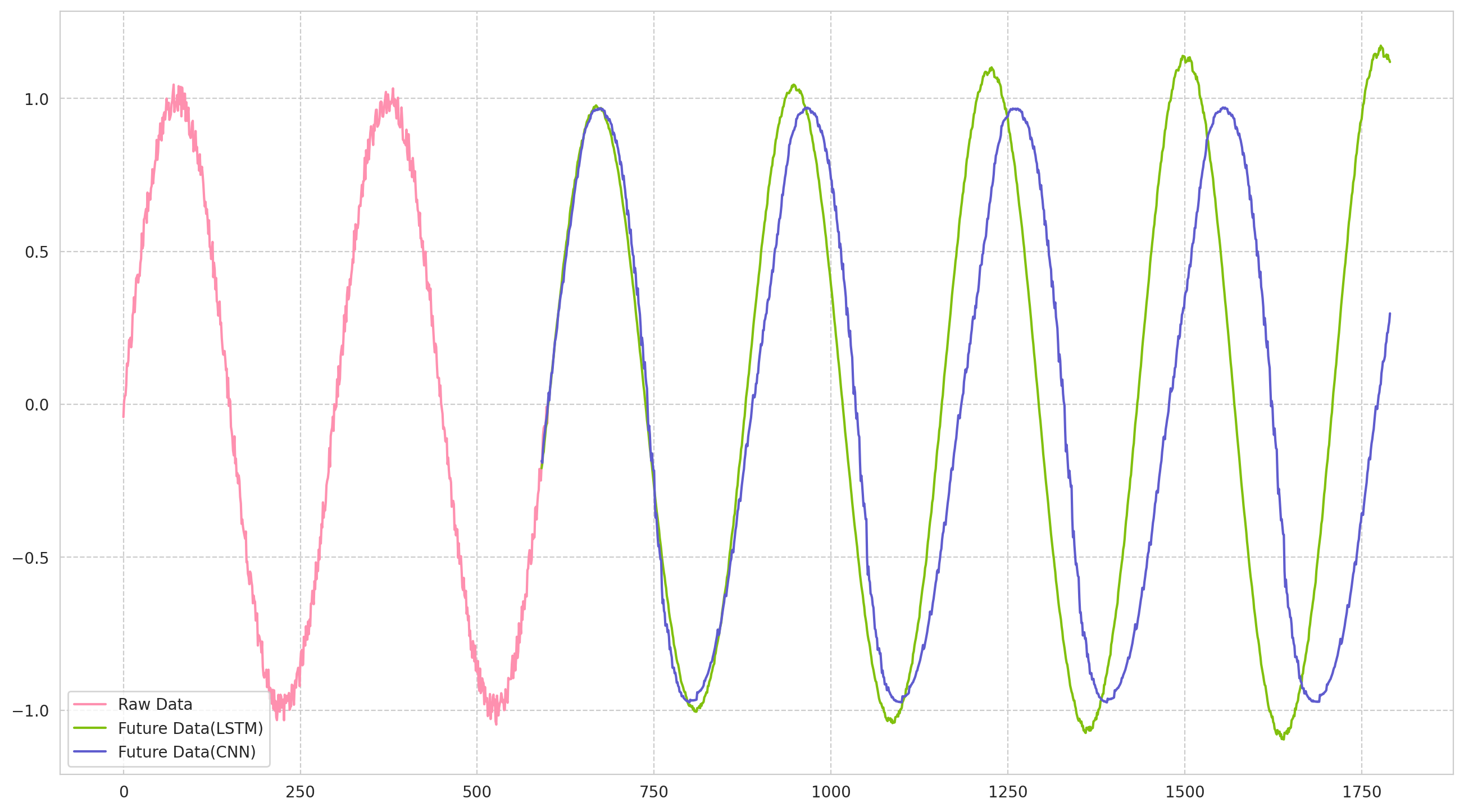
モデルで長めの点を予測する
今は,50ステップの点から,次の1ステップを予測しましたが,
各将来の予測点同士に関連が出にくくなり,時間が経てば程,周期に関する特徴が薄れていっています.
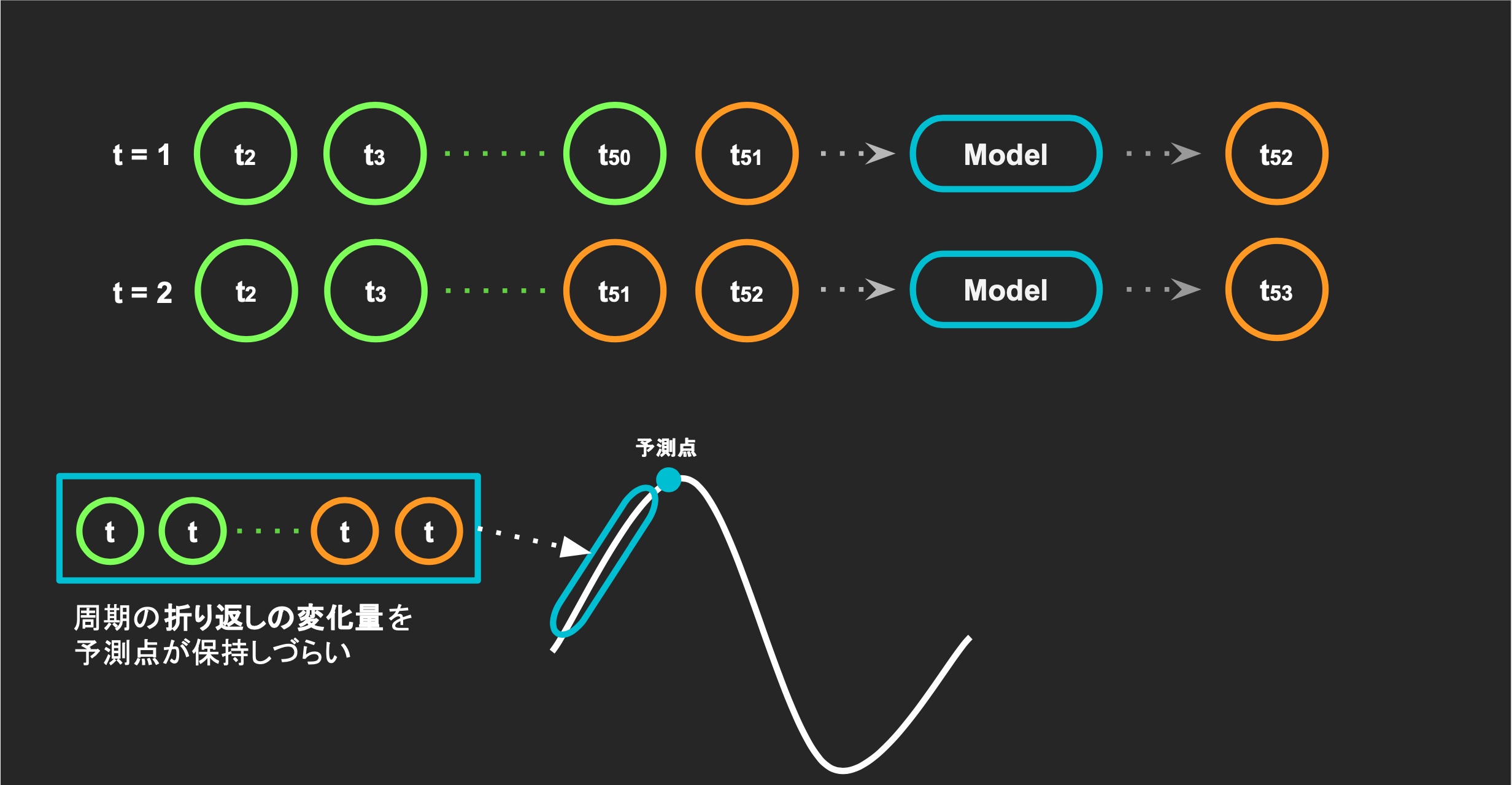
なので,次の10点を予測することで、予測するデータに折り返し等の時系列特徴を保持できないか調べてみます.

10ステップごとに,モデルに投入するデータを更新するコード
long_test = multiple_data[-1].T
long_test_length = long_test.shape[1]
long_cnn_result = np.empty((0))
for step in range(120):
long_test_data = np.reshape(long_test, (1, long_test_length, 1))
batch_predict = multiple_cnn.predict(long_test_data)
long_test = np.delete(long_test, list(range(OUTPUT_LENGTH)))
long_test = np.append(long_test, batch_predict)
long_cnn_result = np.append(long_cnn_result, batch_predict)
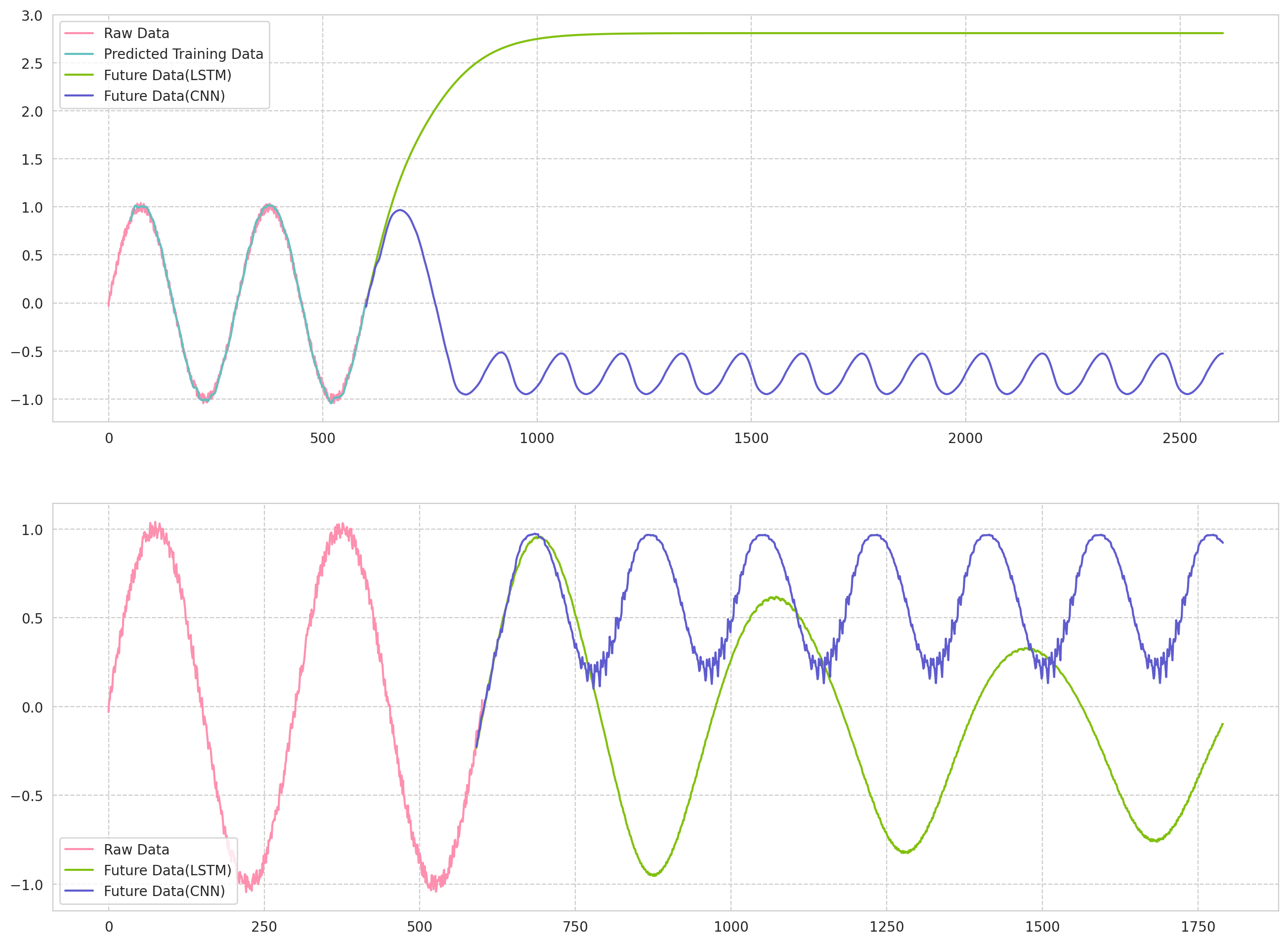
結果
LSTMでは,周期を維持しやすいが,振幅を維持しにくい傾向になり,
1D-CNNは,振幅は維持しやすいが,周期が徐々に長くなっている気がします.
まとめ
今回は,1D-CNNでSin波を予測して,LSTMと比較するために,
Sin波を用意して,長期的な予測をしてみました.
| 1D-CNN | LSTM | |
|---|---|---|
| 周期 | 徐々に長くなりがち | 維持しやすい |
| 振幅 | 値域に収まってる | 発散・収束しやすい |
※ あくまで,一例です.実際に,NumpyとTensorflowの乱数Seedを変更すると.結構めちゃめちゃな推論になったりします.
- 上の図:1ステップを予測
- 下の図:10ステップを予測
もう少し複雑なものでやったり,普通のRNNでやったりしようかなと思います.