こんにちはみなさん。
本記事はKerasアドベントカレンダーの6日目となります。
他の方と比べてしょうもない記事ですが、がんばります。
時系列予測とか時系列解析をするのに、機械学習界隈で一般的な手法はRNN ( リカレントニューラルネットワーク ) だと思うのですが、これの理論て結構難しくて、特にLSTMなんて、私は未だによくわからないし、コードを見てもちんぷんかんぷんです。
そんなの知らなくてもとりあえず動けば問題ないっちゃ問題ないんですが、やっぱりある程度自分が動きを理解できているもののほうが、安心して使えるというものです。
というわけで、一次元畳み込みを使って時系列解析をするという話が出てきているので、kerasを使ってその使い心地を調べてみました。
一次元畳み込み
畳み込み( Convolution ) を使ったニューラルネットワーク ( CNN ) は、今や機械学習の代名詞のようなものですが、CNNといった場合は、暗黙のうちに二次元、つまり画像データに畳み込みフィルターを使ったものを指しているように思います。
2次元畳み込みフィルターは、実際には画像の特徴を表す何らかのパターンを抽出しているということですが、1次元の時系列データ、要するにグラフですが、こいつの中にパターンを見つけ、時系列データの特徴を捉えてしまおうというのが1次元畳み込みフィルターです。
実装
1次元畳み込みが実際に使えるのかどうかを、実装して確かめてみましょう。
Kerasではすでに1次元畳み込みが実装されているので、これを使っちゃいましょう。
問題
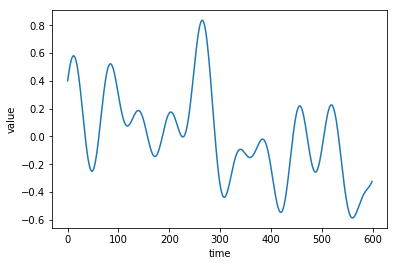
とりあえず、次のようなグラフデータを学習させて、予測器を作りましょう。
このグラフは次の関数で作られています。
f(t) = \frac{1}{5} \left( \sin (t) + \sin (3t) + \sin (10t) + \cos(5t) + \cos (7t) \right)
jupyter で実装
今回は、手っ取り早く以下のDokcerfileのイメージを使ったコンテナを使用して実験します。
FROM tensorflow/tensorflow:latest-py3
RUN pip install keras
$ docker run -it --rm --name keras -p 8888:8888 -p 6006:6006 niisan/keras
超お手軽です。localhost:8888にアクセスすると、jupyterが起動しているので、それを使っていきましょう。
データを準備する
まずはライブラリを読み込みます。
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Dropout
%matplotlib inline
import matplotlib.pyplot as plt
from keras.layers.convolutional import Conv1D, UpSampling1D
from keras.layers.pooling import MaxPooling1D
次に、式に従って時系列データを作成します。
timeline = np.arange(10000)
epochs = 100
def sinnp(n, line):
return np.sin(line * n / 100)
def cosnp(n, line):
return np.cos(line * n / 100)
raw_data = (sinnp(1, timeline) + sinnp(3, timeline) + sinnp(10, timeline) + cosnp(5, timeline) + cosnp(7, timeline)) / 5
raw_data = raw_data + (np.random.rand(len(timeline)) * 0.1)# ノイズ項
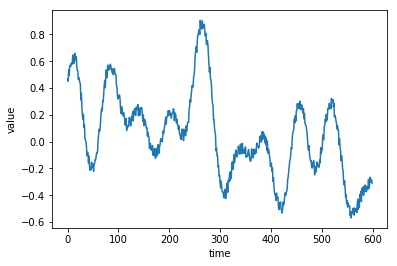
plt.plot(timeline[:600], raw_data[:600])
plt.xlabel("時間")
plt.ylabel("測定値")
plt.show()
これで今回の実験に使うデータは作成完了です。
ここで、わざわざノイズ項をいれていますが、意図的にノイズを入れておいたほうが、結果が良くなるので入れてたりします。
次に、実験における入力と出力を決める必要があります。
今回はこれくらいなら実用性がありそう、という目論見を持って、
「連続した64個の時系列データを元に、次の16個の時系列データを生成する」
と言う機械を作りましょう。
すると、入力と出力は次のように形成すると良いと思います。
input_data = []
output_data = []
for n in range(10000-80):
input_data.append(raw_data[n:n+64])
output_data.append(raw_data[n+64:n+80])
input_data = np.array(input_data)
output_data = np.array(output_data)
print(input_data.shape)
print(output_data.shape)
一応、入力と出力のshapeの状態を確認しておきますが、これは私の趣味みたいなものなので、やらなくてもいいです。
(9920, 64)
(9920, 16)
入力と出力のデータが作れましたが、これではまだ十分ではあありません。
一次元畳み込みでは、データの形状に注意する必要があります。
一次元畳み込みそうにおける入力の形状(shape)は(<シーケンス長>, <パラメータ数>)となっていなければなりません。
今回、グラフを作るためのパラメータの個数、つまり、$f(t)$は一次元なので、パラメータ数は1となります。シーケンス長はサンプルとして取ってくる連続したデータ点の個数となりますので、今回は64となります。
ということで、入力データをちゃんと扱える形に整形します。
train_X = np.reshape(input_data, (-1, 64, 1))
train_Y = np.reshape(output_data, (-1, 16, 1))
print(train_X.shape)
print(train_Y.shape)
(9920, 64, 1)
(9920, 16, 1)
これで、一次元畳み込み層が扱えるデータ形式になりました。
学習器を作る
それでは、学習器を構成する層を積んでみましょう。
model = Sequential()
model.add(Conv1D(64, 8, padding='same', input_shape=(64, 1), activation='relu'))
model.add(MaxPooling1D(2, padding='same'))
model.add(Conv1D(64, 8, padding='same', activation='relu'))
model.add(MaxPooling1D(2, padding='same'))
model.add(Conv1D(32, 8, padding='same', activation='relu'))
model.add(Conv1D(1, 8, padding='same', activation='tanh'))
model.compile(loss='mse', optimizer='adam')
ここでConv1D(filters, kernel_size)が一次元畳み込みを表すそうになります。
Conv1Dの出力層のshapeは (<シーケンス長>, filters)となります。なので、一番はじめの層を見ると、先に設定した入力は
(64, 1) -> (64, 64)というshapeになることがわかります。
また、MaxPooling1Dを使用することで、シーケンス長の部分の次元削減を行います。
最後の層が出力層ですが、ここで今回予測したい出力と次元があうようにしています。
積んだ層がどのようになっているかはsummaryを出すことで確認できます。
model.summary()
Layer (type) Output Shape Param #
=================================================================
conv1d_1 (Conv1D) (None, 64, 64) 576
_________________________________________________________________
max_pooling1d_1 (MaxPooling1 (None, 32, 64) 0
_________________________________________________________________
conv1d_2 (Conv1D) (None, 32, 64) 32832
_________________________________________________________________
max_pooling1d_2 (MaxPooling1 (None, 16, 64) 0
_________________________________________________________________
conv1d_3 (Conv1D) (None, 16, 32) 16416
_________________________________________________________________
conv1d_4 (Conv1D) (None, 16, 1) 257
=================================================================
Total params: 50,081
Trainable params: 50,081
Non-trainable params: 0
_________________________________________________________________
最後の層の出力が期待値として設定した出力の形状と同じなので、今回は全結合しなくて良い感じです。
それでは学習を開始しましょう。
history = model.fit(train_X, train_Y, validation_split=0.1, epochs=epochs)
全データの内、10%をテストデータとして確保することにしました。
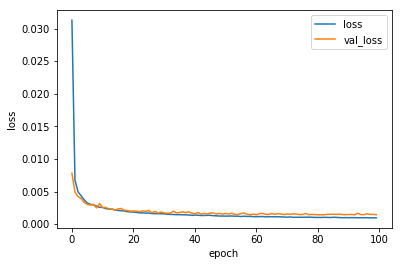
また、学習過程をhistoryに保存しているので、こいつを表示して学習の収束具合を調べてみましょう。
plt.plot(range(epochs), history.history['loss'], label='loss')
plt.plot(range(epochs), history.history['val_loss'], label='val_loss')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend()
plt.show()
流石に単純な関数なので、学習も早いですね。
学習器を使用してみる
学習しただけでは意味がありませんので、軽く使用してみましょう。
今回作ったのは、前の64点から次の16点を導き出す機械ですので、はじめに64点のサンプルを取り出し、それを使って16点を生成したら、その16点を新たにサンプルに加えて、次の16点を生成する・・・を繰り返すジェネレータを作ってみましょう。
今回は20回分、320点先まで予測させてみましょう。
start = 9100
sheed = np.reshape(raw_data[start:start+64], (1, 64, 1))
prediction = sheed
for i in range(20):
res = model.predict(sheed)
sheed = np.concatenate((sheed[:, 16:, :], res), axis=1)
prediction = np.concatenate((prediction, res), axis=1)
次に、予測結果predictionと元のデータを比較しましょう。
グラフに書き出しやすいように、少々データを整形しています。
print(prediction.shape)
predictor = np.reshape(prediction, (-1))
print(predictor.shape)
plt.plot(range(len(predictor)), predictor, label='predict')
plt.plot(range(len(predictor)), raw_data[start:start + len(predictor)], label='real')
plt.legend()
plt.show()
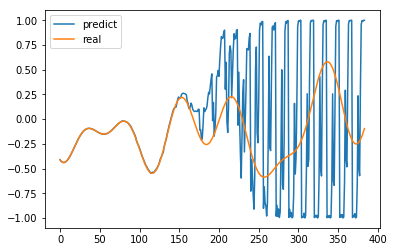
250点前後で、元データとの乖離が激しくなってきていますが、逆を返せば、10回分程度の先読みが
成功していると言ってもいいのではないかと思います。
おまけ - ノイズのない場合
訓練データにノイズがない場合にどうなるのかも面白かったのでやってみましょう。
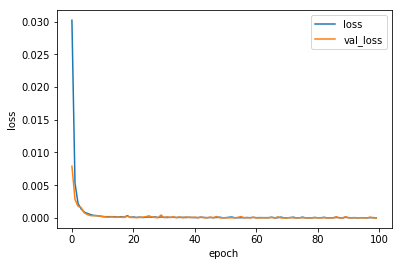
学習曲線は、わかりにくいですが、ノイズありの場合に比べて一桁も精度が良いです。
精度が良いというのが良いことかというと、過学習や「融通の効かなさ」に直結するので、注意が必要です。
試しに先程と同様の条件で予測してみましょう。
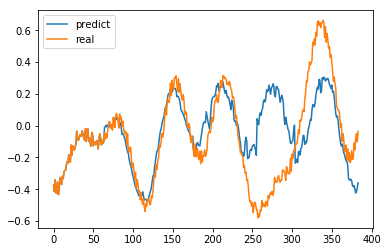
途中まではぴったりと寄り添うように予測できていましたが、150点手前あたりで誤差が大きくなった瞬間に破綻しています。
ノイズを入れることで、ある程度予測誤差が発生することを許容しつつ、大まかな予測が会うようにすることができるようです。
まとめ
一次元畳み込みを使って、簡単な時系列データの予測を行う学習器を作成しました。
学習した結果、ある程度の期間元データと同様の予測をすることができるようになりました。
本当は、この一次元畳み込みを使って音データをオートエンコードしたかったのですが、あまりうまくいかず、まだ検証段階なので、とりあえずその前段階の一次元畳み込みをネタにさせていただきました。
今回はこんなところです。