Go to Qiita Advent Calendar 2024 Top
LoginSignup
4
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@sano192

ABC241 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

Last updated at Posted at 2022-02-27

ABC241(AtCoder Beginner Contest 241)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

パナソニック株式会社様について

本コンテストはパナソニック株式会社様がスポンサードされています。
興味のある方は採用情報を確認してください。

A - Digit Machine

まずaはリストとして受け取りましょう。
リストに格納した場合、akはa[k]と書くことで値を参照できます。

画面に表示されている数字を「k」としましょう。
(1)最初はk=0です。
(2)ボタンを押すと数字はa[k]になります。よってk=a[k]となります。
(3)またボタンを押すと数字はa[k]になります。k=a[k]となります。
(4)またボタンを押すと数字はa[k]になります。k=a[k]となります。
(5)これで3回ボタンを押したことになるので、kを出力します。

つまり3回分k=a[k]と更新すればよいことがわかります。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
a=list(map(int,input().split()))

# 最初に画面に表示されているのは「0」
k=0

# ボタンを押す
k=a[k]

# ボタンを押す
k=a[k]

# ボタンを押す
k=a[k]

# 答えを出力
print(k)

B - Pasta

pythonではremoveという 「リストの中で指定した値と同じ要素を検索し、最初の要素を削除する」 便利な機能があります。
使い方は以下です。
(リスト).remove(検索対象)

ある要素が含まれているかどうかはinで判定できます。
書き方は以下です。
if (検索対象) in (リスト):

この2つを使って、
B[i]がAに含まれるなら→Aから削除
を繰り返します。

最後まで操作ができたら「Yes」、途中でB[i]がAに含まれない状態になったら「No」です。

【提出】

# 入力の受け取り
N,M=map(int,input().split())
A=list(map(int,input().split()))
B=list(map(int,input().split()))

# i=0~(M-1)
for i in range(M):
    # B[i]がAに含まれるなら
    if B[i] in A:
        # Aに含まれるB[i]のうち先頭のものを削除
        A.remove(B[i])
    # そうでないならば(B[i]がAに含まれない)
    else:
        # 「No」を出力
        print("No")
        # 途中終了
        exit()

# 「Yes」を出力
print("Yes")

C - Connect 6

右、下、ななめに6個分のマスを見た時、「#」が4つ以上あるラインが一つでもあれば「Yes」となります。
よって各マスから
・右方向
・下方向
・右下方向
・左下方向
の4方向へ「#」の数を数えれば良いです。

マス目問題は以下のように書くことで2次元配列に各マスの情報を格納できます。

# マス目の情報格納用
grid=[]
# N回
for i in range(N):
    # 文字列で受け取り
    S=input()
    # リストへ展開
    S=list(S)
    # gridへ追加
    grid.append(S)

こうすることでgrid[行番号][列番号]としてマス目の情報を参照することが出来ます。

各方向へ「#」の個数を数える部分はそれぞれ関数にしてしまえば楽です。
マス目からはみ出ないよう、関数を呼び出す前に5個先がマス目の中に収まっているかifで確認します。

計算量はO(N^2)です。実際には各マスについて6マス*4方向=24回の探索が発生するので最大24*(1000)^2≒10^7程度の計算が発生します。
pythonでは間に合わないのでpypyで提出します。

【提出】

# pypyで提出

# 入力の受け取り
N=int(input())

# マス目の情報格納用
grid=[]
# N回
for i in range(N):
    # 文字列で受け取り
    S=input()
    # リストへ展開
    S=list(S)
    # gridへ追加
    grid.append(S)

# 右方向へ「#」を数える
# 引数：行番号,列番号　→　返り値「#」の数
def SearchRight(gyou,retu):
    # 「#」の数
    count=0
    # i=0~5まで
    for i in range(6):
        # マス(行番号,列番号)=「#」ならば
        if grid[gyou][retu+i]=="#":
            # カウント
            count+=1
    # 数を返す
    return count

# 下方向
def SearchDown(gyou,retu):
    count=0
    for i in range(6):
        if grid[gyou+i][retu]=="#":
            count+=1
    return count

# 右下方向
def SearchRightDown(gyou,retu):
    count=0
    for i in range(6):
        if grid[gyou+i][retu+i]=="#":
            count+=1
    return count

# 左下方向
def SearchLeftDown(gyou,retu):
    count=0
    for i in range(6):
        if grid[gyou+i][retu-i]=="#":
            count+=1
    return count

# gyou=0~(N-1)
for gyou in range(N):
    # retu=0~(N-1)
    for retu in range(N):
        # 5マス右がマス目の中に収まっているならば
        if retu+5<N:
            # 「#」の数が4つ以上なら
            if 4<=SearchRight(gyou, retu):
                # 「Yes」を出力
                print("Yes")
                # 終了
                exit()

        # 5マス下がマス目の中に収まっているならば
        if gyou+5<N:
            if 4<=SearchDown(gyou, retu):
                print("Yes")
                exit()

        # 5マス右下がマス目の中に収まっているならば
        if retu+5<N and gyou+5<N:
            if 4<=SearchRightDown(gyou, retu):
                print("Yes")
                exit()

        # 5マス左下がマス目の中に収まっているならば
        if gyou+5<N and 0<=retu-5:
            if 4<=SearchLeftDown(gyou, retu):
                print("Yes")
                exit()

# 「No」を出力
print("No")

D - Sequence Query

あなたがC++を使えるなら迷わず使いましょう。公式解説にある通りC++を使えるならmultisetですぐに解くことが出来ます。
pythonしか使えない人は以下の知識が必要です。

・座標圧縮
・二分探索
・FenwickTreeまたはSegmentTree

例として以下の入力を考えましょう。

Q：8
(1)：1 10
(2)：1 30
(3)：1 50
(4)：1 40
(5)：1 30
(6)：2 45 3
(7)：1 70
(8)：3 60 3

まず素朴なアイデアとして以下の方法があります。
クエリ①：Aが昇順になるよう適切な位置へxを追加
クエリ②,③：xがどの要素の間になるかインデックスを二分探索し、そこからk移動して答えを出力

しかし「Aが昇順になる適切な位置へxを追加」の部分で先頭や真ん中にxを追加することになるとO(N)かかってTLEします。xを追加するたびAをソートする方法も同様です。

そこで「クエリ先読み」を行います。
あらかじめ追加されるxを読み込んで把握しておく方法です。

例えばx=3,5,5,7がくるとわかっているなら
A=[0,0,0,0,0,0,0,0,0,0]
としておき、x=3がきたタイミングで「1」を加算します。
A=[0,0,0,1,0,0,0,0,0,0]
さらに残りx=5,5,7がきたらそれぞれのタイミングで
A=[0,0,0,1,0,2,0,1,0,0]
と「1」を加算していく方法です。これで途中にxを挿入するからO(N)かかる問題は解決できそうに思えます。

しかしxの制約が最大10^18というふざけた数になっています。
これではAは最大10^18の大きさが必要になり、MLE(メモリ制限超過)します。

「クエリ先読み」し、更に「座標圧縮」をかけましょう。
座標圧縮とは「要素」→「小さい方から○番目」というような形で変換できるようにすることです。
例ではクエリ先読みするとx=10,30,50,40,30,45,70,60がくることがわかります。
これらを座標圧縮すると以下のようになります。
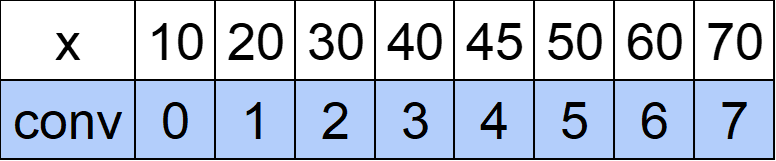
ABC241_D_1.png

convはconvert(変換)の意味です。convを見ることで「x」→「小さい方から○番目」と変換ができます。
このように座標圧縮することでメモリの使用量を大幅に減らせます。

ではどのようにクエリを処理するか考えます。
「(6)：2 45 3」を考えましょう。
(1)~(5)でAに追加されたxは10,30,50,40,30です。これを先ほどと同じ要領で追加された個数分「1」を加算します。
結果をFT行に書きます。
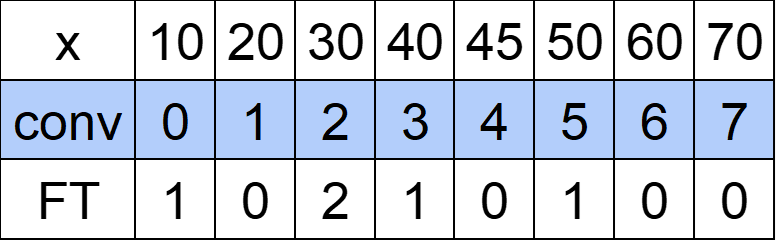
ABC241_D_2.png
(FTはFenwickTreeの意味です)

「(6)：2 45 3」は「45以下の要素のうち大きい方から3番目の数を探しなさい」ということでした。
45からFT行を左に見ていくと40が1個、30が2個あります。合計で3個ですから、3番目にあたる「30」が答えになることがわかります。

一般化すると、
xから左に向かってFTの区間和を取り、k以上になる一番近い場所を探す
という操作で答えが出せます。

言い方を変えると
FT行についてk≤区間和[m,x(のインデックス)]となるうち、最大のm
を探し、
m番目のx(=A[m])が答え
となります。
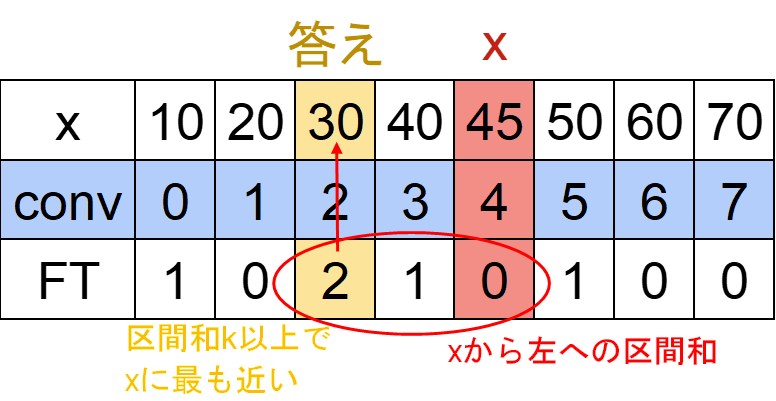
ABC241_D_3.png

クエリ③については上記と全く同じことを右向きに行います。

mの探索には二分探索、区間和計算にはFenwickTreeを使います。

【二分探索を実装したことがない場合】
この問題は二分探索問題としてはかなり難易度が高いため、他の問題で練習してから解くことをおすすめします。
以下が比較的簡単な二分探索問題です。
ABC146 C：https://atcoder.jp/contests/abc146/tasks/abc146_c
ABC231 C：https://atcoder.jp/contests/abc231/tasks/abc231_c
※ABC231 Cは以下で解説をしています。
https://qiita.com/sano192/items/2b2656202b767109387e#c---counting-2

拙著「AtCoder　凡人が『緑』になるための精選50問詳細解説」でも二分探索を詳しく解説しています。
詳しくは本ページ最下部「広告」の部分を御覧ください。

FenwickTreeについてよく知らないという人は以下の解説を読んでください。

FenwickTree
FenwickTreeは数列の要素への加算、区間和計算を高速で行えるデータ構造です。
FenwickTreeについては以下の記事でとてもわかり易くまとめている方がいらっしゃるので興味があれば読んでください。

ただし実装については理解できなくても、以下のclassをコピペして使えれば問題ありません。
灰色～茶色コーダーの方はFenwickTreeの考え方を「ふ～んなるほどね～」くらいで理解しておけば十分です。

class FenwickTree:
    def __init__(self,n):
        self._n=n
        self.data=[0]*n
    def add(self,p,x):
        p+=1
        while p<=self._n:
            self.data[p-1] +=x
            p+=p&-p
    def _sum(self,r):
        s=0
        while 0<r:
            s+=self.data[r-1]
            r-=r&-r
        return s
    def sum(self,l,r):
        r+=1
        return self._sum(r)-self._sum(l)
    def select(self,p):
        return self.sum(p,p)

「使い方」
・初期化【O(N)】：変数名=Fenwick_Tree(要素数)
・加算【O(logN)】：add(インデックス番号,加算する数)
・区間和の計算【O(logN)】：sum(左インデックス番号,右インデックス番号)
・値の参照【O(logN)】：select(インデックス番号)
「使用例」

# 初期化【O(N)】：変数名=Fenwick_Tree(要素数)
FT=FenwickTree(10)

# 加算【O(logN)】：add(インデックス番号,加算する数)
FT.add(0,4)
FT.add(5,-1)
FT.add(7,3)

# 区間和の計算【O(logN)】：sum(左インデックス番号,右インデックス番号)
print(FT.sum(2,8))

# 値の参照【O(logN)】：select(インデックス番号)
print(FT.select(7))

pythonでは間に合わないのでpypyで提出します。

【提出】

# pypyで出力

class FenwickTree:
    def __init__(self,n):
        self._n=n
        self.data=[0]*n
    def add(self,p,x):
        p+=1
        while p<=self._n:
            self.data[p-1] +=x
            p+=p&-p
    def _sum(self,r):
        s=0
        while 0<r:
            s+=self.data[r-1]
            r-=r&-r
        return s
    def sum(self,l,r):
        r+=1
        return self._sum(r)-self._sum(l)
    def select(self,p):
        return self.sum(p,p)

# 入力の受け取り
Q=int(input())
# クエリの情報格納用
querys=[]

# Aを用意(重複除去のためセット)
A=set()

# Q回
for i in range(Q):
    # クエリを読み込み
    tmp=list(map(int,input().split()))
    # 記録
    querys.append(tmp)
    # xをAへ追加
    x=tmp[1]
    A.add(x)

# Aの長さをNとする
N=len(A)

# リストへ変換してソート
A=list(A)
A.sort()

# 変換用連想配列
conv=dict()

# i=0~(Aの長さ-1)
for i in range(len(A)):
    # 変換表を作成
    # 「x」→「Aの小さい方から○番目」
    conv[A[i]]=i

# 左方向への区間和計算
# 引数：変換後のxのインデックス,k　→　返り値：k≤区間和[m,x(のインデックス)]となるうち、最大のm
def Nibutan_left(x_index,k):
    # 左端(left)
    l=0
    # 右端(right)
    r=x_index

    # 1<右-左の間
    while 1<r-l:
        # 中央(center)
        c=(l+r)//2
        # 区間和[c,x_index]を計算
        # k以上なら
        if k<=FT.sum(c,x_index):
            # 左=中央と更新
            l=c
        # k以下なら
        else:
            # 右=中央と更新
            r=c

    # k≤区間和[r,x_index]ならば
    if k<=FT.sum(r,x_index):
        # rが一番近い
        return r
    # k≤区間和[l,x_index]ならば
    elif k<=FT.sum(l,x_index):
        # lが一番近い
        return l
    # どちらでもない
    else:
        # k≤区間和[m,x(のインデックス)]となるmが存在しない
        return -1

# 右方向への区間和計算
def Nibutan_right(x_index,k):
    l=x_index
    r=N-1
    while 1<r-l:
        c=(l+r)//2
        if k<=FT.sum(x_index,c):
            r=c
        else:
            l=c

    if k<=FT.sum(x_index,l):
        return l
    elif k<=FT.sum(x_index,r):
        return r
    else:
        return -1

# FenwickTreeを用意
FT=FenwickTree(10**6)

# Q回
for i in range(Q):
    # クエリ①
    if querys[i][0]==1:
        x=querys[i][1]
        # FTに加算
        FT.add(conv[x],1)

    # クエリ②
    elif querys[i][0]==2:
        x=querys[i][1]
        k=querys[i][2]
        # FTについてk≤区間和[m,x(のインデックス)]となるうち、最大のm
        m=Nibutan_left(conv[x],k)

        # k≤区間和[m,x(のインデックス)]となるmが存在しない
        if m==-1:
            # 「-1」を出力
            print(-1)
        else:
            # 答えを出力
            print(A[m])

    # クエリ③
    else:
        x=querys[i][1]
        k=querys[i][2]
        # FTについてk≤区間和[x(のインデックス),m]となるうち、最小のm
        m=Nibutan_right(conv[x],k)

        if m==-1:
            print(-1)
        else:
            print(A[m])

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb

【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW

【booth(pdf】
https://sano192.booth.pm/items/3785312

4
1
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
1

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?