ABC217 A～E問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC217(AtCoder Beginner Contest 217)　A～E問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

A - Lexicographic Order

辞書順かどうか？を判定するわけですがpythonでは
if S<T:
と書くことで辞書順かどうかの判定ができます。
SがTより辞書順で早ければTrue,そうでなければFalseとしてくれるのであとはそれぞれYes,Noを出力すればOKです。

上記の内容を知らない場合、「python 辞書順 判定」などと検索することで判定方法を確認することができます。
それでもわからなければこの問題は飛ばしてさっさとB問題へ進みましょう。

なお、問題文には

主要なプログラミング言語の多くでは、文字列の辞書順による比較は標準ライブラリに含まれる関数や演算子として実装されています。詳しくは各言語のリファレンスをご参照ください。

と記載がありますがリファレンスはだいたいの場合検索性が悪く、更に内容が難しすぎて何を言っているかわかりません。
灰色や茶色コーダーの人はgoogleで検索して個人ブログやQiitaの記事を探しましょう。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力を受け取る
S,T=map(str, input().split())
# もし辞書順でS<Tならば
if S<T:
    # Yesを出力
    print("Yes")
# そうでないならば(辞書順でT<Sならば)
else:
    # Noを出力
    print("No")

B - AtCoder Quiz

単純にABC,ARC,AGC,AHCという変数を用意し、あれば1、なければ0に変更する、という方法で解けます。
ですがせっかくB問題なのでもう少しかっこいい方法を使いましょう。

ABCがS1,S2,S3に含まれているか？は以下のif分で判定できます。

if "ABC" in [S1,S2,S3]:

今回は含まれていない場合はーという処理にしたいのでこれにnotをつければOKです。

if "ABC" not in [S1,S2,S3]:

あとはABC,ARC,AGC,AHCそれぞれについて同じ判定をすれば解けます。

【提出】

# 入力の受け取り
S1=input()
S2=input()
S3=input()

# もしABCがS1,S2,S3に含まれていなければ
if "ABC" not in [S1,S2,S3]:
    # ABCを出力
    print("ABC")
# もしARCがS1,S2,S3に含まれていなければ   
elif "ARC" not in [S1,S2,S3]:
    # ARCを出力
    print("ARC")
# もしAGCがS1,S2,S3に含まれていなければ
elif "AGC" not in [S1,S2,S3]:
    # AGCを出力
    print("AGC")
# もしAHCがS1,S2,S3に含まれていなければ
elif "AHC" not in [S1,S2,S3]:
    # AHCを出力
    print("AHC")

C - Inverse of Permutation

QのPi番目の要素がiである、という部分をそのままコードにできればよいです。
つまり
Q[P[i]]=i
とすればよいです。
コツは先にQを用意しておくことです。
Q=[0]*(N+1)
とすることで要素が全て0で、要素数がNの配列を作ることができます。これを作ってから各Q[i]を埋めます。

※注意点1
pythonの配列は0番から始まるため、普通に
P=list(map(int, input().split()))
とするとP[0]=p1,P[1]=p2,...と番号がずれます。
P[0]をてきとうな数字(0など)で埋めるため
P=[0]+list(map(int, input().split()))
とするのがよいです。

※注意点2
Q[0]は答えの出力時、不要です。こういった場合はQ[1:]とすることで「Q[1]から後ろを出力する」とできます。

※注意点3
出力時
print(Q[1:])
ではなく、
print(*Q[1:])
と書くことで余計な[]をつけずに出力することができます。

【提出】

# 入力の受け取り
N=int(input())
# P[0]を埋めるため、[0]+にする
P=[0]+list(map(int, input().split()))

# Qを用意
Q=[0]*(N+1)

# i=1~Nまで
for i in range(1,N+1):
    # Q[P[i]]=iを順に埋める
    Q[P[i]]=i

# 答えを出力
# *(リスト)にすると[]なしで出力
# Q[0]は不要なのでQ[1:](1以降を出力)
print(*Q[1:])

D - Cutting Woods

あなたがC++を使えるならC++を使いましょう。公式解説にある通り、C++のstd::setを使えばいとも簡単に解くことができます。

残念ながらpythonしか使えなかった場合、以下の知識が必要です。
・二分探索
・座標圧縮(defaultdictを使う)
・FenwickTreeまたはSegmentTree(区間和の高速計算)
かなり難易度は高いです。頑張りましょう。

例として以下の入力を考えましょう。
20 8
1 12
2 7
1 2
1 5
1 18
1 16
1 10
2 6

(1)愚直解法
制約が一切なかった場合、つまりTLEもMLEもなかったとすればどのように解けるか考えます。
まずcut=[0,20(=L)]として「切った場所リスト」を用意します。
c=1のクエリが来たらcutに値を格納していきます。
8番目のクエリが来た時点でcutは以下のようになっています。
cut=[0,20,12,2,5,18,16,10]
これをソートします。
cut=[0,2,5,10,12,16,18,20]
そしてx=6がどの値の間にあるか確認します。
左端から順に要素を見ていくと5と10の間にあることがわかります。
故にx=6が含まれる木材は長さ5(=10-5)です。

この解法の問題は以下です。
Nをcutの長さとしてクエリ一回あたり
・ソートがO(NlogN)
・xがどの値の間にあるか探索にO(N)
当然TLEします。

(2)二分探索する
(1)で「xがどの値の間にあるか探索」する時、数列はソートされているのだから二分探索が使えるでしょう。これなら
Nをcutの長さとして
・ソートがO(NlogN)
・xがどの値の間にあるか、二分探索してO(logN)
と少し改善できます。
ですがソートに時間がかかってTLEします。

【二分探索を実装したことがない場合】
この問題は二分探索問題としてはかなり難易度が高いため、他の問題で練習してから解くことをおすすめします。
以下が比較的簡単な二分探索問題です。
ABC 146 C：https://atcoder.jp/contests/abc146/tasks/abc146_c
ABC 216 E：https://atcoder.jp/contests/abc216/tasks/abc216_e
※ABC 216 Eは以下で解説をしています。
https://qiita.com/sano192/items/edb3e2293b9c649ad282

拙著「AtCoder　凡人が『緑』になるための精選50問詳細解説」でも二分探索を詳しく解説しています。
詳しくは本ページ最下部「広告」の部分を御覧ください。

(3)ソートの代わりに切ったところで1を立てる
cut=[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
みたいな配列(cut=[0]*(L+1))を作って、C=1のときに切ったところ(=cut[x])に1を立てます。
8番目のクエリの場合、カットした場所は右端(0)、左端(L)を含めると0,2,5,10,12,16,18,20なので
cut=[1,0,1,0,0,1,0,0,0,0,1,0,1,0,0,0,1,0,1,0,1]
となります。
c=2,x=6が来たら
cut[6]から左に1が立っているところにぶつかるまで探索(c[5]=1)
cut[6]から右に1が立っているところにぶつかるまで探索(c[7]=0,c[8]=0,c[9]=0,c[10]=1)
これならソートせずに長さは測れます。
ですが左右へ1が立っている場所への探索にO(N)かかります。
しかもLは最大で10^9なので
・cutの配列サイズが最大10^9
でMLE(メモリ制限超過)します。

問題点は
・左右に1が立っている場所を探しにいくのにO(N)
・cut配列でかすぎ
というところです。

(4)座標圧縮してcutを小さくする
まずcut配列のサイズをなんとかしましょう。
Lは最大10^9ですが、Qは最大2*10^5です。
以下のように考えます。
①Qを先に全部読み込む(記録しておく)
②c=1のときのxを全てcutへ記録する。
③cutをソート
④cutの値⇔インデックス番号と変換できるようにする。

この状態でクエリを読み直します。
・c=1,x=12が来た時
　x=12(cutの12)→index=4と変換→cut済[4]に1を立てる

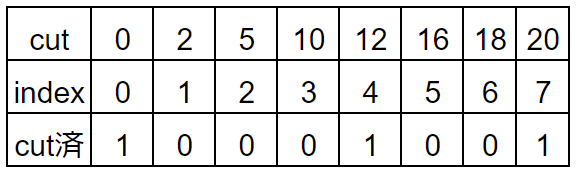
このように
・cutの値とindexの値を相互変換できるようにする
・カットされたタイミングでcut済に1を立てる
とすることでメモリ使用量を減らすことができます。
このようなやり方を座標圧縮といいます。

※座標圧縮についてはdefaultdictを使います。defaultdictを使ったことがない人は以下を読んでください。

defaultdict(連想配列)について
辞書または連想配列と言います。
キー：値
というような対応付を行えるデータ構造です。(辞書という言い方もします)
連想配列はdict()と書くことでも使えますがデフォルトの値(初期値)が設定できません。そのため存在チェックなど色々面倒が発生します。
その面倒を避けるためにdefaultdictを使います。
import：from collections import defaultdict
作成(デフォルト0)：変数名=defaultdict(int)
キー、値の登録：変数名[キー]=値
値の取り出し：変数名[キー]
【使用例】

# インポート
from collections import defaultdict

# 作成(デフォルト0)：変数名=defaultdict(int)
dictionary=defaultdict(int)

# キー、値の登録：変数名[キー]=値
dictionary[5]=1

# 値の取り出し：変数名[キー]
x=dictionary[5]

詳しく知りたい人は以下を参照してください。

・c=2,x=7が来た時
　x=7がcutのどの値の間にあるか二分探索→5と10の間
　5→index=2と変換
　10→index=3と変換
　
　index=2からcut済を左方向へ探索→index=0がcut済=1
　index=0をcutの値へ変換→0
　
　index=3からcut済を右方向へ探索→index=4がcut済=1
　index=4をcutの値へ変換→12
　
　答えは12(12-0)

これでcntのサイズが最大10^5*2程度で済むのでメモリ問題は解決です。
しかし
・左右に1が立っている場所を探しにいくのにO(N)
が残っています。

(5)FenwickTreeで「1を左右へ探しに行く」部分を二分探索
最後に残った問題は要するに以下が解決できればよいです。
「ある場所から左(右)で一番近くに1が立っている場所を高速で探すにはどうしたらよいか？」

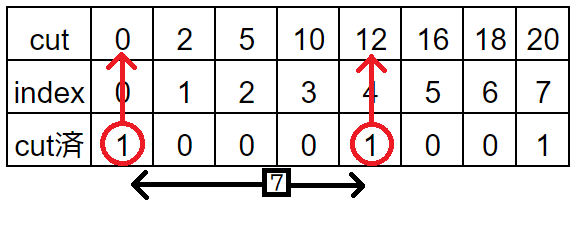
例として2番目のクエリでは以下を探す必要があります
・index=2からcut済を左方向へ探索→1が立っている一番近いインデックス
・index=3からcut済を右方向へ探索→1が立っている一番近いインデックス
図の場合であれば左方向はindex=0、右方向はindex=4です。
これがわかればそこからcutの値へ変換、長さを引き算(12-0)したら答えが出ます。

この探索のため区間和を計算しましょう。

・左方向
index0~2のちょうど真ん中index1までの和を確認します。
すなわちindex1~2までのcut済みの区間和です。
これは0です(0+0)
0ということはこの区間に1はありません。

なので探索範囲を広げます。今度はindex0～2まで広げてみます。
すなわちindex0~2までのcut済みの区間和です。
これは1です(1+0+0)
1以上なのでこの区間には少なくとも1が1つ以上あります。

と、いう感じで index○~左 の区間和を確認するとその間に1があるかを確認できます。
(区間和が1以上ならその区間に少なくともひとつ1がある、0ならその区間に1はない)
1がある区間 index○~左 のうち、○が一番大きい(近い)ものを探すわけです。

今回の場合、index0がcut済=1であるもののうち一番近いものだとわかります。

・右方向
index3~7のちょうど真ん中index5までの和を確認します。
すなわちindex3~5までのcut済みの区間和です。
これは1です(0+1+0)
1以上なのでこの区間には少なくとも1が1つ以上あります。

なので探索範囲を狭めます。今度はindex3～4まで狭めます。
すなわちindex3~4までのcut済みの区間和です。
これは1です(0+1)
1以上なのでこの区間には少なくとも1が1つ以上あります。

と、いう感じで index右~○ の区間和を確認するとその間に1があるかを確認できます。
(区間和が1以上ならその区間に少なくともひとつ1がある、0ならその区間に1はない)
1がある区間 index右~○ のうち、○が一番小さい(近い)ものを探すわけです。

今回の場合、index4がcut済=1であるもののうち一番近いものだとわかります。

この○をまたそれぞれ二分探索するわけです。
index○~左のcut済区間和が1以上になるうち最大の○(一番近い1の場所)
index右~○のcut済区間和が1以上になるうち最小の○(一番近い1の場所)

しかしまともに区間和を求めていたらTLEします。
そういうわけで区間和の探索はFenwickTreeを使います。

FenwickTreeは
・要素の加算：O(log(N))
・区間和計算：O(log(N))
で行うことができるデータ構造です。

FenwickTreeについては以下の記事でとてもわかり易くまとめている方がいらっしゃるので確認してください。
ただし実装については理解できなくても以下のclassをコピペで構いません。
この問題を解くにあたってはFenwickTreeの考え方を「ふ～んなるほどね～」くらいで理解し、コピペで使えればよいです。

FenwickTreeのクラス内容については『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』にて詳細に解説しています。
内容までしっかり理解したいという人は購入をご検討ください。
詳しくは【広告】をご覧ください

# Fenwick_Tree
class Fenwick_Tree:
    # 初期化(要素数n)
    def __init__(self,n):
        self._n=n
        self.data=[0]*n
    # pにxを追加
    def add(self,p,x):
        p+=1
        while p<=self._n:
            self.data[p-1] +=x
            p+=p&-p
    # [0,r)の区間和を計算
    def _sum(self,r):
        s=0
        while 0<r:
            s+=self.data[r-1]
            r-=r&-r
        return s
    # [l,r]の区間和を計算
    def sum(self,l,r):
        r+=1
        return self._sum(r)-self._sum(l)

使い方は上記をコードの最初にコピペして
・初期化：変数名=Fenwick_Tree(要素の長さ)
・加算：変数名.add(インデックス番号,加算する数)
・区間和：変数名.sum(左インデックス番号,右インデックス番号)
【使用例】

# 初期化：変数名=Fenwick_Tree(要素の長さ)
Fenwick=Fenwick_Tree(100)

# 加算：変数名.add(インデックス番号,加算する数)
Fenwick.add(10,5)
Fenwick.add(20,10)
Fenwick.add(30,20)

# 区間和：変数名.sum(左インデックス番号,右インデックス番号)
x=Fenwick.sum(10,25)

ここまで来てようやく解けます。もう一度手順を書きます。
(1)クエリを先読みしてカットする場所の情報をcutへ格納
(2)cutをソート
(3)cutとindex番号の変換表を作成(座標圧縮)
(4)クエリを読み直し
c=1なら
(5)xの座標を確認→FenwickTreeで該当のインデックス番号に1を立てる(1を加算)
c=2なら
(6)二分探索(Nibutan_x)　xがどの要素の間にあるか(left_i,right_iの間)
(7)二分探索(Nibutan_low)　○~left_iの区間和をFenwickTreeで計算→一番近い1のインデックス番号(区間和が1以上となる最大の○)
(8)二分探索(Nibutan_high)　right_i~○の区間和をFenwickTreeで計算→一番近い1のインデックス番号(区間和が1以上となる最小の○)
(9)一番近い1が立っているindex番号→cutの値へ変換
(10)右端-左端をして答えを出力

なお、pythonでは間に合わないのでpypyで提出します。

【提出】

# 提出はpypyで行う

# Fenwick_Tree
class Fenwick_Tree:
    # 初期化(要素数n)
    def __init__(self,n):
        self._n=n
        self.data=[0]*n
    # pにxを追加
    def add(self,p,x):
        p+=1
        while p<=self._n:
            self.data[p-1] +=x
            p+=p&-p
    # [0,r)の区間和を計算
    def _sum(self,r):
        s=0
        while 0<r:
            s+=self.data[r-1]
            r-=r&-r
        return s
    # [l,r]の区間和を計算
    def sum(self,l,r):
        r+=1
        return self._sum(r)-self._sum(l)

# 入力の受け取り
L,Q=map(int, input().split())
# クエリの記録用リスト
query=[]
# カットする場所を予め記録するリスト
cut=[]
# Q回
for i in range(Q):
    # 入力の受け取り
    c,x=map(int, input().split())
    # クエリを記録
    query.append([c,x])
    # カットならば
    if c==1:
        # cutに場所を記録
        cut.append(x)

# cutに左端=0を追加
cut.append(0)
# cutに右端=Lを追加
cut.append(L)

# cutをソート
cut.sort()

# cutの長さをcut_Nとする
cut_N=len(cut)

# defaultdictのインポート
from collections import defaultdict
# x(カットする場所)→インデックス番号への変換
cut_indx=defaultdict(int)
# インデックス番号→x(カットする場所)への変換
indx_cut=defaultdict(int)

# 変換表の作成
for i in range(cut_N):
    cut_indx[cut[i]]=i
    indx_cut[i]=cut[i]

# FenwickTreeの作成
Fenwick=Fenwick_Tree(cut_N)

# 左端(0)に1を立てる(1を足す)
Fenwick.add(cut_indx[0],1)
# 右端(Lのインデックス番号)に1を立てる(1を足す)
Fenwick.add(cut_indx[L],1)

# xがどのインデックス番号の間にあるか確認する二分探索
def Nibutan_x(x):
    # 左端=0
    left=0
    # 右端=cut_N-1
    right=cut_N-1

    # 1<right-leftの間
    while 1<right-left:
        # 真ん中(center)=(left+right)//2
        center=(left+right)//2
        # インデックス番号→カットする場所へ変換した値がxより小さいなら
        if indx_cut[center]<x:
            # 左端=center
            left=center
        # インデックス番号→カットする場所へ変換した値がxより大きいなら
        else:
            # 右端=center
            right=center
    
    # xの左、右のインデックス番号を返す
    return left,right

# iより左で1が立っている場所のうち、一番近いものを二分探索
def Nibutan_low(i):
    # 左端=0
    left=0
    # 右端=i
    right=i

    # 1<right-leftの間
    while 1<right-left:
        # 真ん中(center)=(left+right)//2
        center=(left+right)//2
        # center~iの和が1以上=center~iの間に1が1つ以上立っている
        if 1<=Fenwick.sum(center,i):
            # 左端=center
            left=center
        # center~iの和が1より小さい=center~iの間に1が立っていない
        else:
            # 右端=center
            right=center

    # i~rightの和が1ならば(right=iになっている時、i~iの和が1ならば)
    if Fenwick.sum(i,right)==1:
        # rightを返す
        return right
    # そうでないならば
    else:
        # leftを返す
        return left

# iより右で1が立っている場所のうち、一番近いものを二分探索
def Nibutan_high(i):
    # 左端=i
    left=i
    # 右端=cut_N-1
    right=cut_N-1

    # 1<right-leftの間
    while 1<right-left:
        # 真ん中(center)=(left+right)//2
        center=(left+right)//2
        # i~centerの和が1以上=i~centerの間に1が1つ以上立っている
        if 1<=Fenwick.sum(i,center):
            # 右端=center
            right=center
        # i~centerの和が1より小さい=i~centerの間に1が立っていない        
        else:
            # 左端=center
            left=center
    # left~iの和が1ならば(left=iになっている時、i~iの和が1ならば)
    if Fenwick.sum(left,i)==1:
        # leftを返す
        return left
    # そうでないならば
    else:
        # rightを返す
        return right

# クエリを読み込み
for c,x in query:
    # c=1の場合
    if c==1:
        # cut_indx[i]の部分に1を立てる(+1する)
        Fenwick.add(cut_indx[x],1)
    # c=2の場合
    else:
        # xがどのインデックス番号の間にあるか確認する二分探索
        left_i,right_i=Nibutan_x(x)
        # xより左で1が立っている場所のうち、一番近い場所のインデックス番号を二分探索
        left_indx=Nibutan_low(left_i)
        # インデックス番号→実際のカットされた場所へ変換
        left_x=indx_cut[left_indx]
        # xより右で1が立っている場所のうち、一番近い場所のインデックス番号を二分探索        
        right_indx=Nibutan_high(right_i)
        # インデックス番号→実際のカットされた場所へ変換
        right_x=indx_cut[right_indx]
        # 右の値-左の値
        print(right_x-left_x)

##E - Sorting Queries

いちいち昇順ソートしてたら当然間に合わないのでなんとかしましょう。
昇順ソートと書いていますがクエリ2では最小値が出せれば良さそうなのでheapを使います。

以下のようにすることで解けます。
○heapとdequeを用意

・クエリ1
dequeにxを格納

・クエリ2
heapに要素があれば
・heapから取り出して出力
そうでないなら(heapが空なら)
・dequeから取り出して出力

・クエリ3
dequeの中身全部をheapへぶち込む

dequeについて
dequeはリストのようなものですが、先頭から要素を取り出す操作をO(1)で行うことができます。
(リストだとO(N)かかります)
import：from collections import deque
作成：変数名=deque()
末尾に要素追加 O(1)：変数名.append(要素)
先頭から要素を取り出して削除 O(1)：変数名.popleft()
【使用例】

# インポート
from collections import deque

# 作成：変数名=deque()
que=deque()

# 末尾に要素追加 O(1)：変数名.append(要素)
que.append(1)

# 先頭から要素を取り出して削除 O(1)：変数名.popleft()
x=que.popleft()

詳しく知りたい人は以下のページを見てください。

heapについて
heapはリストから最小値をO(logN)で取り出せるデータ構造です。
import：import heapq
リストのheap化 O(N)：heapq.heapify(リスト)
要素の追加 O(logN)：heappush(リスト,要素)
最小値の取り出し O(logN)：heappop(リスト)
【使用例】

# インポート
import heapq

# リストを用意
que=list()

# リストのheap化 O(N)：heapq.heapify(リスト)
heapq.heapify(que)

# 要素の追加 O(logN)：heappush(リスト,要素)
heapq.heappush(que, 6)
heapq.heappush(que, 1)

# 最小値の取り出し O(logN)：heappop(リスト)
min_x=heapq.heappop(que)

詳しく知りたい人は以下のページを見てください。

【提出】

# 入力の受け取り
Q=int(input())
# キューを用意
from collections import deque
que=deque()
# heapqを用意
import heapq
heap_que=list()

# Q回
for i in range(Q):
    # クエリの受け取り(長さがクエリの種類によって違うためとりあえずリストで)
    query=list(map(int, input().split()))
    # クエリ 1,x
    if query[0]==1:
        # xを取り出し
        x=query[1]
        # キューに格納
        que.append(x)
    # クエリ 2
    elif query[0]==2:
        # もしheap_queに要素があれば
        if 0<len(heap_que):
            # heap_queから取り出し
            ans=heapq.heappop(heap_que)
        # heap_queが空なら
        else:
            # queから取り出し
            ans=que.popleft()
        # 答えを出力
        print(ans)
    # クエリ 3
    else:
        # キューの要素を全てheap_queへ入れ直す
        for i in range(len(que)):
            heapq.heappush(heap_que, que.popleft())

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】