パナソニックプログラミングコンテスト2021(ABC231) A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

パナソニックプログラミングコンテスト2021(AtCoder Beginner Contest 231)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

パナソニック株式会社様について

このコンテストはパナソニック株式会社様が主催されています。
「パナソニックがAtCoderユーザーを必要としている理由」「AtCoderで鍛えた力を活かせるパナソニックの仕事」などがコンテストトップページより確認できます。

興味がある人は採用情報をご覧ください。

A - Water Pressure

問題文の指示通り(D/100)を計算して出力しましょう。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
D=int(input())

# D/100を出力
print(D/100)

B - Election

Sをリストに受け取り、それぞれの候補者名がいくつあるかを確認します。
(リスト).count(候補者名)
とすることでリストに「候補者名」がいくつあるか、すなわち何票獲得したかを確認できます。

候補者の種類はセットで受け取るとよいです。
セットはリストと違い、重複した要素を入れることができません。
(セットに("a","b")が入っている場合、"a"を追加しても何も起こりません)
そのためセットにS1,S2,...を追加していくことで候補者の一覧を作ることができます。
セットを作るときは
変数名=set()
追加するときは
変数名.add(候補者名)
と書きます。

セットの要素それぞれについて処理を行うときは
for 変数名 in (候補者名セット):
と書きます。こうすることで(候補者名セット)の要素を順に「変数名」へ入れて処理できます。

具体的な実装手順は以下です。
(1)投票先を入れるリスト、候補者一覧のセットを作る
(2)入力を受け取り、リスト、セットへ追加していく
(3)それぞれの候補者について、得票数(リストに名前がいくつあるか)を確認する
　それまでに最も得票数が多かった候補より得票数が多かったら答えを更新する
(4)答えを出力する

【提出】

# 入力の受け取り
N=int(input())

# 投票先
candidate=[]
# 候補者の種類
Names=set()

# N回
for i in range(N):
    # 入力の受け取り
    S=input()
    # 投票先を記録
    candidate.append(S)
    # セットに追加(重複不可)
    Names.add(S)

# 答え候補者名
ans_Name=""
# 得票数
ans_votes=0

# 候補者それぞれについて
for Name in Names:
    # 候補者Nameの得票数
    votes=candidate.count(Name)
    # 暫定の答え候補者より得票数が多ければ
    if ans_votes<votes:
        # 答えを更新
        ans_Name=Name
        # 得票数を更新
        ans_votes=votes

# 答えを出力
print(ans_Name)

C - Counting 2

二分探索で解きます。

まずAをソートします。
xがAのどの要素の間にあるかわかれば答えが出ます。A[k-1]<x≤A[k]であれば(N-k)人が答えです。
(ただしAは0インデックス、すなわち先頭をA[0],その次をA[1],...としています)

xがAの最小の要素以下ならば答えはN人です。
xがAの最大の要素より大きければ答えは0人です。
これらでなければ二分探索で確認します。

まず
左端インデックス=0
右端インデックス=N-1
とします。

左端と右端の真ん中、すなわち(左端+右端)//2のAの要素を確認します。
A[真ん中]<x　ならば　左端インデックス=真ん中　と更新します。
x≤A[真ん中]　ならば　右端インデックス=真ん中　と更新します。
この処理を右端と左端の差が1になるまで繰り返します。

コツは常に
A[左端]<x
x≤A[右端]
となるようにしておくことです。

差が1になったとき、A[左端]<x≤A[右端]となっていますから、(N-右端インデックス)が答えです。

例を見ましょう。
N：6
A：1 2 5 10 15 20
x：7

左端インデックス=0
右端インデックス=5
真ん中(0+5)//2=2
A[2]=5で、これはx=7より小さいです。よって
左端インデックス=2と更新します。

左端インデックス=2
右端インデックス=5
真ん中インデックス=(2+5)//2=3
A[3]=10で、これはx=5以上です。よって
右端インデックス=3と更新します。

左端インデックス=2
右端インデックス=3
(右端)-(左端)=1となったので終了です。
つまりA[2]<x≤A[3]であることがわかりました。
よって答えは(N-右端)=6-3=3であることがわかります。
(x≤A[3],A[4],A[5]となっています)

【提出】

# 入力の受け取り
N,Q=map(int,input().split())
A=list(map(int,input().split()))

# Aをソート
A.sort()

# 二分探索
# 引数：x　返り値：身長がx以上の生徒の人数
def Nibutan(x):
    # x≤A[0](最も小さいAの要素)ならば
    if x<=A[0]:
        # N人
        return N
    # A[N-1](最も大きいAの要素)<xならば
    elif A[N-1]<x:
        # 0人
        return 0
    # 左端(常にA[left]<x)
    left=0
    # 右端(常にx≤A[right])
    right=N-1

    # 1<右端-左端の間
    while 1<right-left:
        # 真ん中
        center=(left+right)//2
        # もしA[center]<xならば
        if A[center]<x:
            # 左端を真ん中へ更新
            left=center
        # そうでなければ(x≤A[center])
        else:
            # 右端を真ん中へ更新
            right=center
        
    # (N-右端)人
    return N-right

# Q回
for i in range(Q):
    # 入力の受け取り
    x=int(input())
    # 答えの出力
    print(Nibutan(x))

D - Neighbors

UnionFindを使います

隣合わなければならない人をグラフで描いて考えてみます。

例えば(1,2),(2,3),(3,4)が隣り合う場合は以下のようになります。

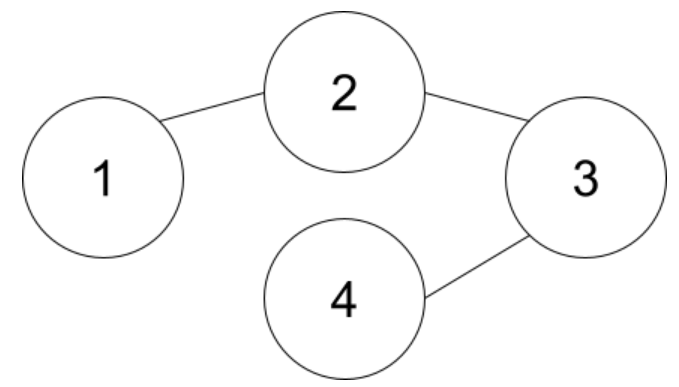
「No」となるケースを考えましょう。「No」となるケースは以下の2つです。
・1つの頂点から3本以上の辺が出ている
(1,2),(2,3),(3,4),(2,4)だと②は①,③,④と隣り合う必要がありますが当然無理です。このケースはグラフにすると以下のように1つの頂点から3本以上の辺が出ているケースに当たります。

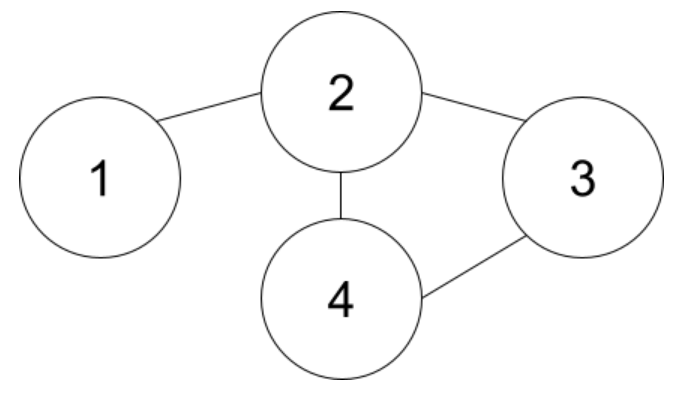
・ループがある
(1,2),(2,3),(3,4),(1,4)だと円形に並ばなければならないですがそれは無理です。このケースは頂点を順番に進んで戻ってしまう場合、すなわちループがある場合に当たります。
(こういったグラフを「閉路がある」といいます)

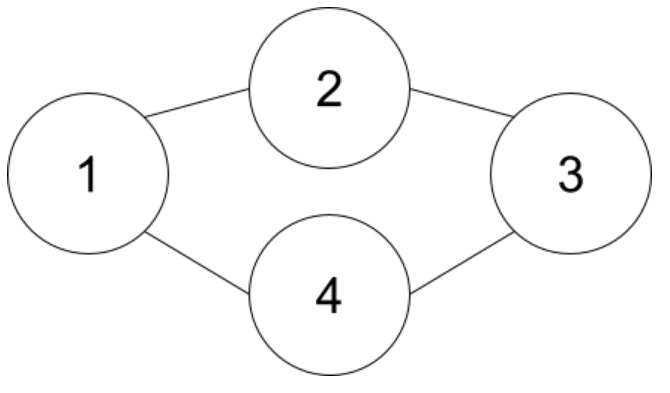
この2つの条件に当てはまらなければ「Yes」となります。それぞれの条件をどのように判定するか考えます。
・1つの頂点から3本以上の辺が出ている
これは簡単で、各頂点から出ている辺の数を入力を受け取りながらカウントすればよいです。辺の数が3本を超えた時点で「No」となります。

・ループがある
UnionFindで確認します。

UnionFindはグループ分けを高速でできるデータ構造です。
具体的には以下のことができます。
・a,bを同じグループとする⇔a,bを連結する：【O(logN)くらい】(厳密には違いますがO(logN)くらいと思っておけばOKです)
・a,bが同じグループか判定する⇔a,bが連結か確認する：【O(1)くらい】(厳密には違いますがO(1)くらいと思っておけばOKです)
とにかくめちゃくちゃ速く上記2つができるデータ構造だと覚えましょう。

きちんとした説明はAtCoder公式が解説スライドを作っているのでそちらを御覧ください。

UnionFindの実装はかなり難しいです。ですが問題を解くのにそこまで理解する必要はなく、以下のUnionFindクラスをコピペして使えればOKです。

# UnionFind
class UnionFind:
    def __init__(self,n):
        self.n=n
        self.parent_size=[-1]*n
 
    def leader(self,a):
        if self.parent_size[a]<0: return a
        self.parent_size[a]=self.leader(self.parent_size[a])
        return self.parent_size[a]
 
    def merge(self,a,b):
        x,y=self.leader(a),self.leader(b)
        if x == y: return 
        if abs(self.parent_size[x])<abs(self.parent_size[y]):x,y=y,x
        self.parent_size[x] += self.parent_size[y]
        self.parent_size[y]=x
        return 
 
    def same(self,a,b):
        return self.leader(a) == self.leader(b)
 
    def size(self,a):
        return abs(self.parent_size[self.leader(a)])
 
    def groups(self):
        result=[[] for _ in range(self.n)]
        for i in range(self.n):
            result[self.leader(i)].append(i)
        return [r for r in result if r != []]

上記をコードの最初にコピペしてから以下のように使います。
・初期化：変数名=UnionFind(要素の数)
・グループリーダー(根)の確認：変数名.leader(要素番号)
・グループ化：変数名.merge(要素番号1,要素番号2)
・同一グループかの確認：変数名.same(要素番号1,要素番号2)
　(同一ならTrue,違うグループならFalseを返す)
・所属するグループのサイズ確認：変数名.size(要素番号)
・グループ全体の確認：変数名.groups()

【初期化時の注意事項】
本問のように頂点の番号が1から始まる場合、
初期化：変数名=UnionFind(N+1)
としなければならないことに注意してください。
このクラスは頂点番号が0インデックスでの使用を想定しているためです。

【使用例】

# 初期化：変数名=UnionFind(要素の数)
UF=UnionFind(10)

# グループ化：変数名.merge(要素番号1,要素番号2)
UF.merge(0,2)
UF.merge(1,3)
UF.merge(3,0)

# グループリーダー(根)の確認：変数名.leader(要素番号)
leader_x=UF.leader(1)

# 同一グループかの確認：変数名.same(要素番号1,要素番号2)
if UF.same(1,5)==True:
    print("同一グループ")
else:
    print("別グループ")

# 所属するグループのサイズ確認：変数名.size(要素番号)
size_x=UF.size(1)

# グループ全体の確認：変数名.groups()
print(UF.groups())

連結とは頂点同士をいくつかの辺を使って行き来できる、すなわち頂点同士がつながっているということです。
A,Bをグループ化、というのが頂点の連結、すなわちA,Bに辺を張るということを意味します。

UnionFindを使って
・頂点の連結
・頂点がすでに連結かの判定
を行います。すでに連結の頂点にさらに辺を張るとループになります。
例えば以下のグラフではすでに頂点②,④は連結です。

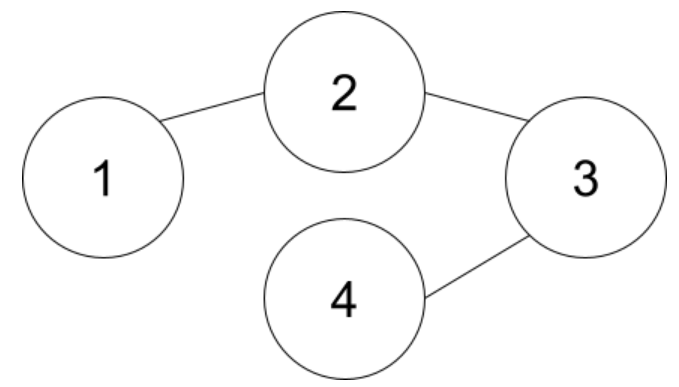
もしここに②-④の辺を張ると②-③-④がループになることがわかります。これは「No」のパターンです。

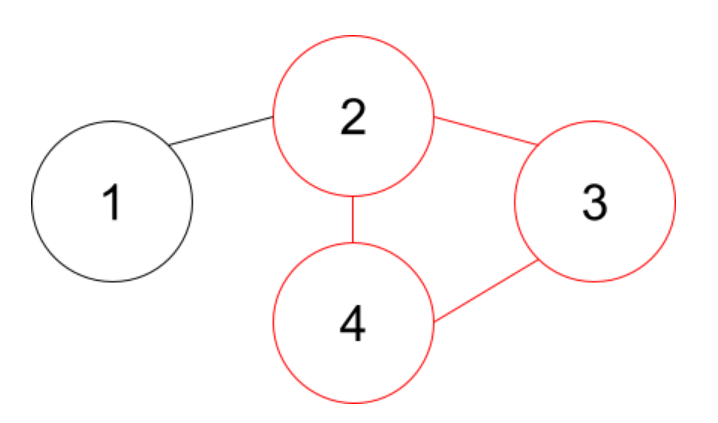
よって以下のように処理を行います。
・A,Bが非連結ならば
　A,Bを連結する
・A,Bがすでに連結ならば
　「No」を出力する

【提出】

# UnionFind
class UnionFind:
    def __init__(self,n):
        self.n=n
        self.parent_size=[-1]*n

    def leader(self,a):
        if self.parent_size[a]<0: return a
        self.parent_size[a]=self.leader(self.parent_size[a])
        return self.parent_size[a]

    def merge(self,a,b):
        x,y=self.leader(a),self.leader(b)
        if x == y: return 
        if abs(self.parent_size[x])<abs(self.parent_size[y]):x,y=y,x
        self.parent_size[x] += self.parent_size[y]
        self.parent_size[y]=x
        return 

    def same(self,a,b):
        return self.leader(a) == self.leader(b)

    def size(self,a):
        return abs(self.parent_size[self.leader(a)])

    def groups(self):
        result=[[] for _ in range(self.n)]
        for i in range(self.n):
            result[self.leader(i)].append(i)
        return [r for r in result if r != []]

# 入力の受け取り
N,M=map(int,input().split())

# UnionFind　初期化
UF=UnionFind(N+1)

# 辺の本数をカウント
count=[0]*(N+1)

# M回
for i in range(M):
    # 入力の受け取り
    A,B=map(int,input().split())
    # 辺の本数をカウント
    count[A]+=1
    count[B]+=1
    # 辺の本数が3本以上なら
    if 3<=count[A] or 3<=count[B]:
        # 「No」を出力
        print("No")
        # 終了
        exit()
    # A,Bが連結なら
    if UF.same(A,B)==True:
        # 「No」を出力
        print("No")
        # 終了
        exit()
    # そうでなければ(非連結なら)
    else:
        # A,Bに辺を張る(連結する)
        UF.merge(A,B)

# 「Yes」を出力
print("Yes")

UnionFindのより詳細な説明、クラスの内容の解説については拙著『AtCoder　凡人が『緑』になるための精選50問詳細解説』に記載しています。
内容までしっかり理解しておきたいという人は購入をご検討ください。
詳細は本ページ下部【広告】を御覧ください。

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

1～24問目まではサンプルとして無料公開しています

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】

【booth(pdf)】

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。

【kindle】

【booth(pdf】