機械学習初心者でも、ニューラルネットワーク(neural network : NN)について理解しなければならない日がいつか来る。なので初心者代表の私が、ニューラルネットワークについて初心者なりに分かりにくいところなどを含め解釈したものをまとめてみました。
加筆修正のコメント等あれば、遠慮なく教えてください。
本記事は、初心者の初心者による初心者のためのニューラルネットワーク#4〜理論:パラメータ更新編〜の続きとなりますが、内容として連動しているわけではありません。
1. なぜ人はニューラルネットワークを学ぶのか
今や日常生活の様々な場面に用いられている、機械学習のコアの部分だからです。(多分)
2. 本記事の目的
本記事では、学習アルゴリズムの大枠を理解したところで、そもそも分類問題における学習とはなんのことだったかについて概観します。ここで振り返ることによって、ニューラルネットワークが具体的にどのような動きをアルゴリズム上で行なっているのかについての理解が深まると思います。
3. 前記事の要約
初心者の初心者による初心者のためのニューラルネットワーク〜理論:順伝播編〜では、ニューラルネットワークの基本概念、基本構造そしてアルゴリズム①である順伝播(forward-propagation)について説明しました。
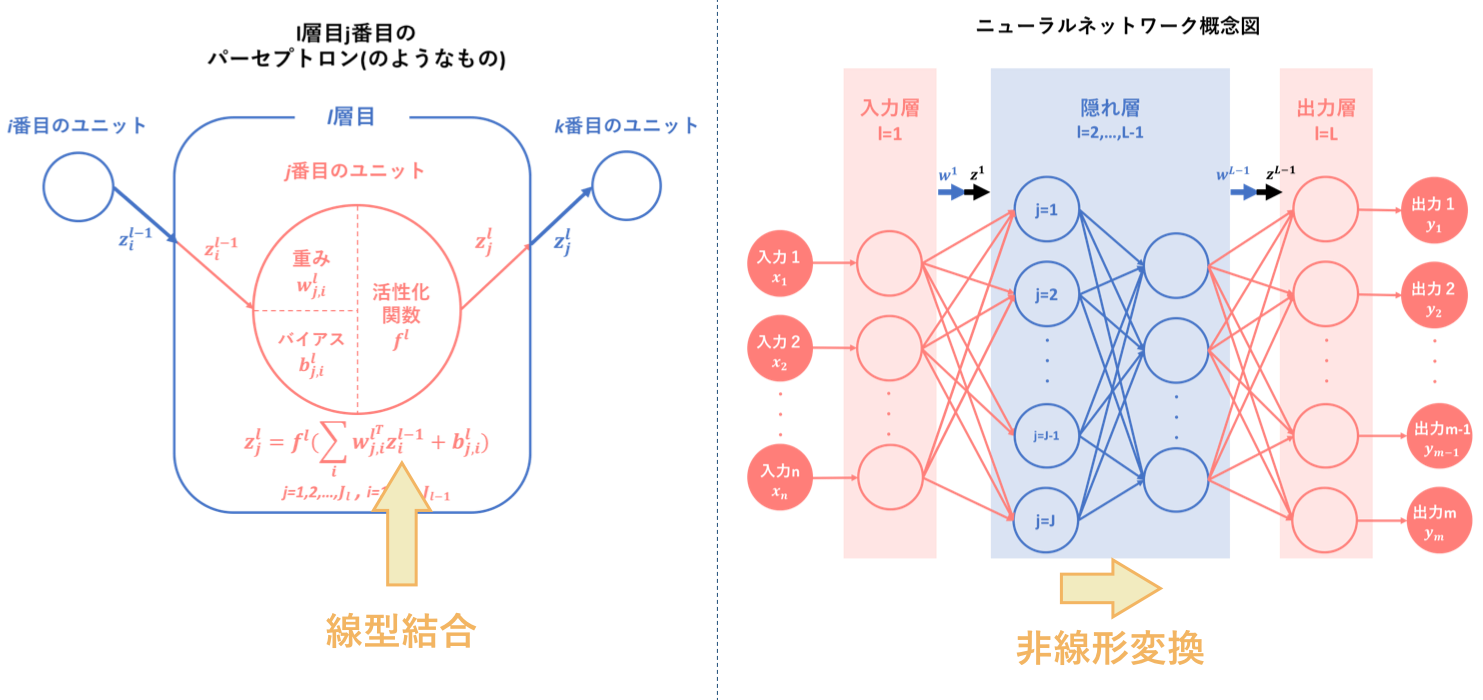
その要約として以下の図をあげます。ニューラルネットワークとは、『パーセプトロン(のようなもの)を基に人間の脳神経系のニューロンを数理モデル化したもの』のことであり、『線型結合と非線形変換を繰り返す合成関数 $f(w,x)$によって入力から出力を表すモデル』です。
そして、ニューラルネットワークの目的は最適パラメータの発見であり、そのために学習を繰り返すことによって予測出力を最適化するようなパラメータを導出します。
順伝播は、その学習アルゴリズムの一つ目でした。
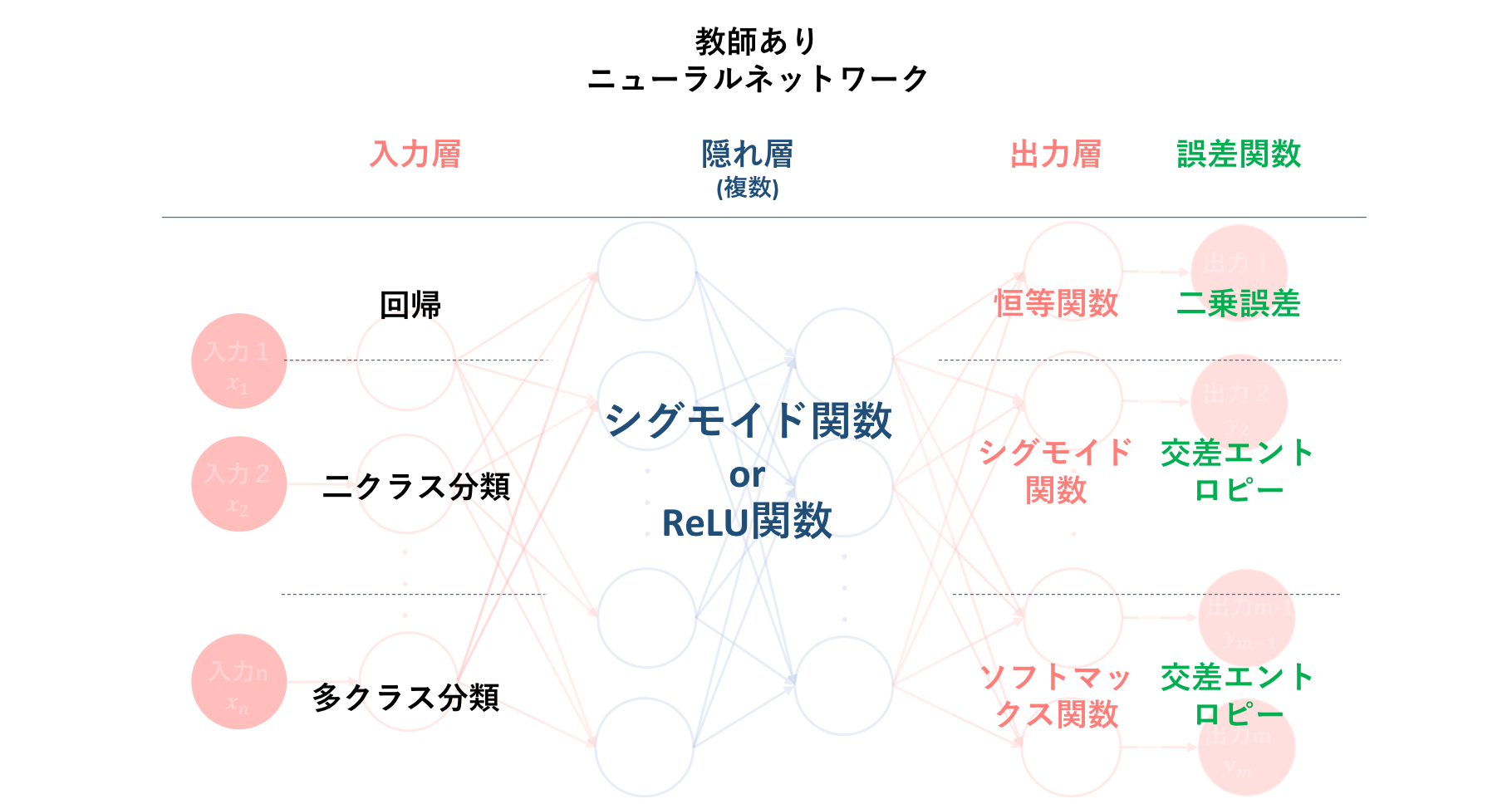
そして続く初心者の初心者による初心者のためのニューラルネットワーク〜理論:誤差計算編〜では、アルゴリズム②である出力値と教師信号のずれの程度を表すための誤差計算について説明しました。そして、こちらはアルゴリズム②には含まれない部分ですが、誤差関数と密接に関係する多層パーセプトロン内の活性化関数の種類とその使用場面についての説明も行いました。
以下の図は、それらの誤差関数および活性化関数の種類と、それぞれどのような問題に対し用いることが一般的なのかをまとめたものになります。
これに基づいた誤差計算は、学習アルゴリズムの二つ目でした。
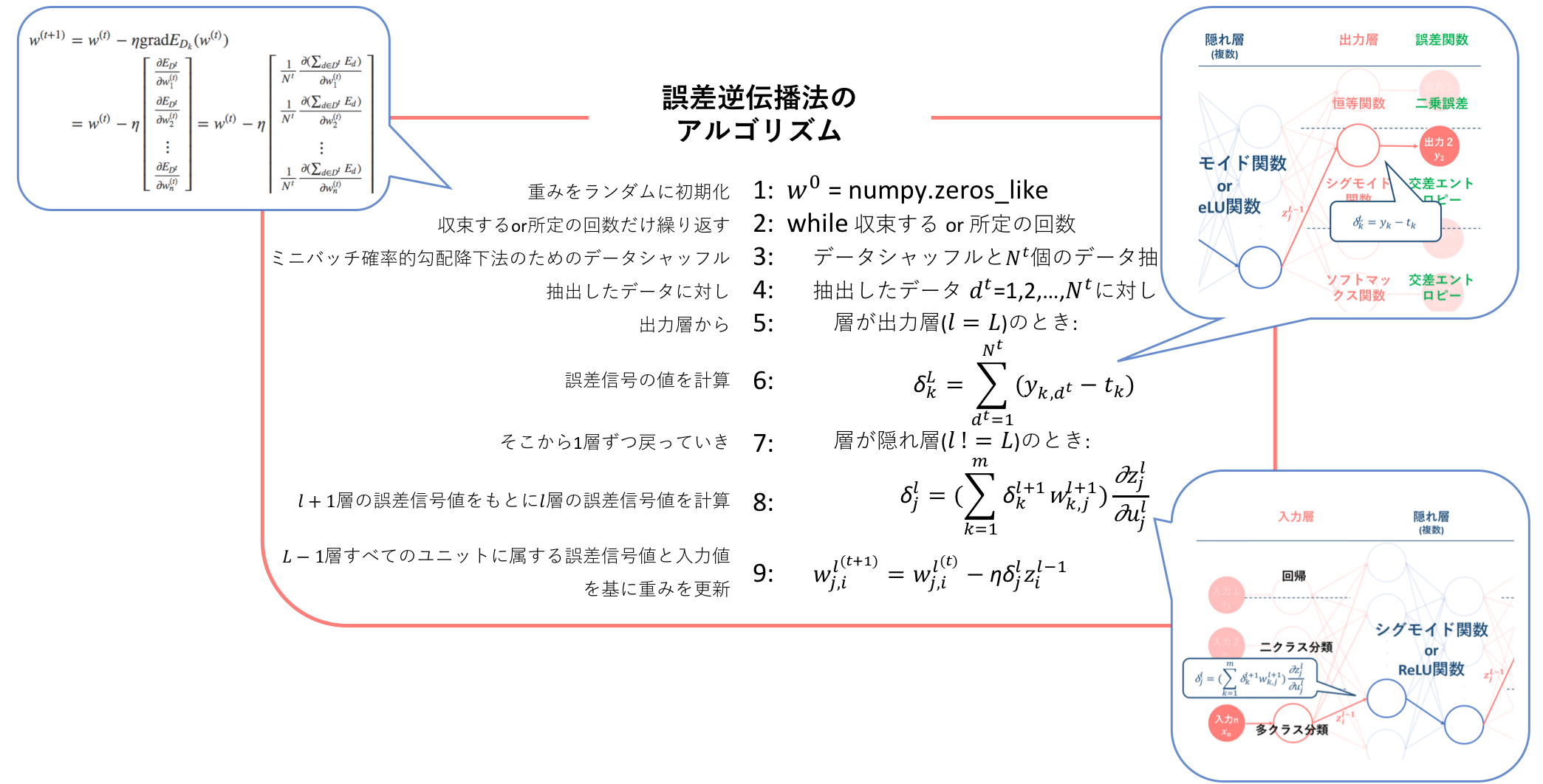
そして、初心者の初心者による初心者のためのニューラルネットワーク#3〜理論:逆伝播編〜では、誤差を最小化するための学習方法として勾配降下法を適用するために、各層における誤差関数の重みに対する勾配の計算方法を導出しました。その結果、$l$層の勾配を算出するには$l+1$層の誤差信号及び$l$層への入力値を求める必要があることが分かりました。これによって、勾配降下法の多層パーセプトロン(この記事ではニューラルネットワークと同義)への適用には、あらかじめ
・ 順伝搬による各層の出力の算出
・ 出力値と教師信号の比較による誤差信号の算出
という二つのフェーズ、すなわち多層パーセプトロンアルゴリズムの①, ②をパスしなくてはいけないことが分かりました。
以下の図は、それぞれの活性化関数及び誤差関数を用いた場合の勾配の計算式を示したものです。なお、前記事の議論から、誤差信号は三つの出力関数には依らないということが分かっています。
この勾配の導出が、学習アルゴリズムの三つ目でした。
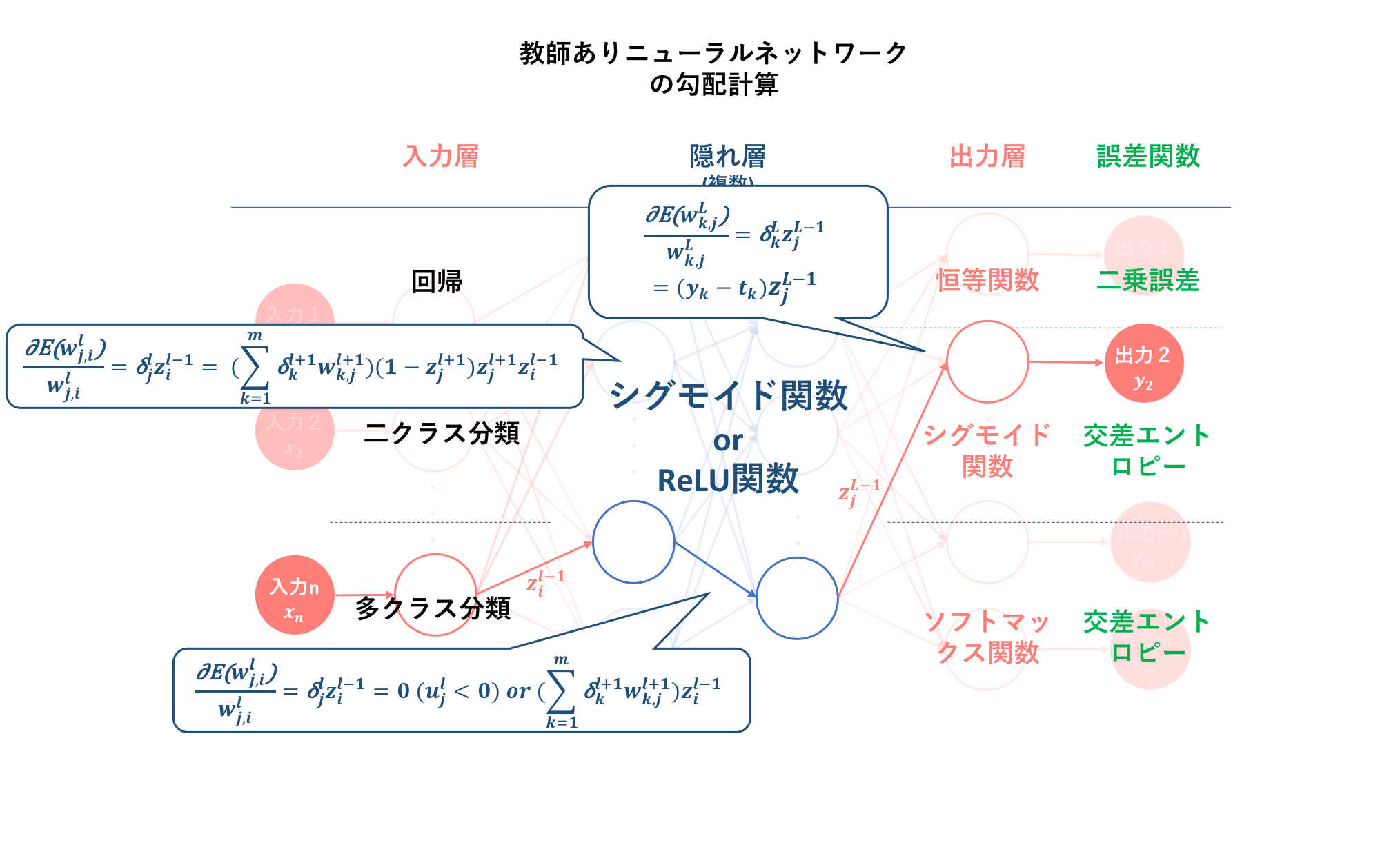
そして、学習アルゴリズムの最後である初心者の初心者による初心者のためのニューラルネットワーク#4〜理論:パラメータ更新編〜では、#3.で導出した誤差関数$E$の重み$w$に対する勾配式を勾配降下法に適用することによって、重み$w$の更新式を導出しました。そして、この逆伝播からパラメータ更新までのフローを表した手法を誤差逆伝播法(backpropagation)とし、そのアルゴリズムを示しました。そして、この誤差逆伝播法のアルゴリズムこそが、ニューラルネットワークの学習アルゴリズムになります。
4. ニューラルネットワークやSVMにおける分類問題の解釈
ニューラルネットワークでは、以上のようなアルゴリズムフローを経ることによって学習を行い、最適モデルを導出しようとしていくこととなります。しかしここで一つ、実装に関する説明を行う前に、ニューラルネットワークなどの分類問題を解くうえで必要となる解釈について述べておきたいと思います。この解釈はニューラルネットワークだけでなく、SVM(サポートベクターマシン)の理解にも貢献します。
また本章は、日頃から参照させて頂いているHELLO CYBERNETICSさんのSVM、ニューラルネットなどに共通する分類問題における考え方の要約となります。
4.1. データ自由度と超平面(識別境界)次元との関係
分類問題における最大の目的は、入力データの次元を変化させながら、正確に線形分離できるような超平面を見つけることです。
まず一般に分類問題を考えるとき、**『$n$次元空間の識別境界は$(n-1)$次元の超平面』**ということが前提として成り立ちます。これには、$n$次元データの自由度が大きく関係します。
4.1.1. 自由度
では、そもそも自由度とは何のことなのでしょうか。$n$次元データの自由度は$(n-1)$である、というのはよく耳にするような話ですが、なぜ"-1"する必要があるのでしょうか。
これについて、以下で簡単に具体例を混ぜて解説します。
$$x_1+x_2+x_3=y$$
上式のように、3次元の入力データによって出力が一意に定まる状況を仮定します。そのような場合、例えば$x_1=1$, $x_2=2$, $y=6$としたとき、入力データは未だ2次元分しか仮定されていないのにも関わらず、$x_3$の値は一意に定まってしまいます。
$$1+2+x_3=6$$
つまり、3次元の入力データに対し、2次元分を自由に指定してしまえば残りの1次元は自ずと定まることとなります。そしてこれは$n$次元に拡張しても、同様のロジックで自由に指定できるデータは$(n-1)$次元分ということになります。
つまり自由度とは、入力に対し出力が一意に定まる状況において自由に指定することができる入力データの次元数のことであり、$n$次元データに対してその自由度は$(n-1)$となります。これが、$n$次元データの自由度は$(n-1)$となる理由です。
4.1.2. 自由度と超平面次元
では、その自由度が、識別境界である超平面の次元に対してどのように関係するのでしょうか。
入力データの次元を$(x_1, x_2,...,x_n)$,出力を$y$とすれば、入力と出力の関係は、関数$f$を用いて
$$f(x_1, x_2, ...,x_n)=y$$
という式で表されます。そしてこの$n$次元空間における超平面は、定数Aを用いて、
$$f(x_1, x_2, ...,x_n)=\text{A}$$
で表されます。そして、出力$y$をこの$\text{A}$と比較することによって分類を行うわけです。つまり、定数$\text{A}$はあらかじめ定められていますから、先ほどの自由度の議論から入力データの自由度は$n-1$であり、つまり超平面の次元は自由度と等しく$(n-1)$となります。
4.2. 非線形な分類問題における学習の解釈
前節の議論から、**『$n$次元空間の識別境界は$(n-1)$次元の超平面となる』**ことが分かりました。それでは、このことを少し掘り下げてみましょう。
4.2.1. n+1以上の高次元空間への写像
『$n$次元空間の識別境界は$(n-1)$次元の超平面となる』ことが意味するのは、$n$次元空間での分類の際、その分離平面は必ずしも線形である必要がないということです。つまり、現実問題手に入れられるデータはそのままでは線形分離できないようなものが多いですが、超平面は非線形なものになり得るので分離可能となります。
そして、実はこの『非線形な平面によって識別境界を定める』というのは、ある考え方と等価になります。それは、**『データがプロットされた空間を高次元空間に写像し、写像した空間で線形分離する』**というものです。
以下の画像(→SVM、ニューラルネットなどに共通する分類問題における考え方から転載)を見てもらえれば、そのイメージを掴みやすいのではないでしょうか。

また、さらに実用的な例として以下が紹介されていました。

つまり上の例を一般化すれば、$n$次元空間にプロットされたデータを線形分離することが難しい場合、$(n+1)$次元空間に一度データを写像しその空間内で一旦線形分離をし、次にその超平面を元の次元に逆写像することによって$n$次元空間での非線形分離を行なっていることになります。
そしてこの写像は次元の数に依らないので、$n$次元から$(n+a)$次元への写像⇄逆写像を行うことによっても$n$次元空間での非線形分離が可能となります。
以上をまとめると、**『$n$次元空間に$(n-1)$次元の非線形分離超平面を設けることは、$(n+a)$次元空間に$(n+a-1)$次元の線形分離超平面を設けることで補うことができる』**ことになります。そして、次元を上げれば上げるほど、元の$n$次元では複雑になるような非線形分離超平面を線形分離超平面から求めることができるようになります。つまり、高次元に写像することは、$n$次元にプロットされたデータの分離可能性(=精度)を高めることに貢献します。
4.2.2. 非線形分類問題における学習とは
さて、それでは本章のまとめに入ります。本章では、『$n$次元空間に$(n-1)$次元の非線形分離超平面を設けることは、$(n+a)$次元空間に$(n+a-1)$次元の線形分離超平面を設けることで補うことができる』ことについて言及しました。
しかし、一体どの次元に写像すれば良いのでしょうか。実は、このような適切な次元を見つけることこそが、分類問題における学習の役割です。つまり、**分類問題における学習問題の根幹の役割とは、『線形分離ができないような状況で、線形分離ができるような高次元空間を発見すること』**となります。線形分離可能な状況になれば、境界を決めるのは簡単です。引くための目安やルールさえ決めてしまえば、境界は簡単に求めることができます。
ニューラルネットワークは、出力次元への変換だけでなく、誤差逆伝播法によって高次元への変換までも学習に含めることで分離性能を向上させました。一方サポートベクターマシンは、無限次元への埋め込みを実現することによって、高い汎化性能で実用化に至りました。
再度ですが、SVM、ニューラルネットなどに共通する分類問題における考え方にも非常に分かりやすく説明されているので、そちらも合わせてご参照ください。
5. まとめ
本記事では、ニューラルネットワークやSVMの分類問題における『学習』について再確認しました。学習とは、パラメータを決定することである、識別境界としての超平面を求めることである...etc様々に捉えられます。しかし、その**根幹にあるのは、『線形分離可能な写像先空間の発見』そして『その空間内での線形分離』**です。これをユニット間で連続して繰り返すことで、最適パラメーターを求めようとしていくわけです。
次の記事では、ニューラルネットワークの実装時の学習工夫について説明する予定です。