1. 本記事の目的
本記事では、ランダムフォレストについて理論的な説明を詳しくしていきます。
最近は深層学習を用いた研究が活発ですが、まだランダムフォレストの適用がふさわしい場面も多々あると言われています。そこで本記事では、気軽に利用できる機械学習アルゴリズムであるランダムフォレストへの理解を深めることで、より応用的な活用を可能にすることを目的とします。
加筆修正の必要箇所がございましたら、是非ご指摘頂けると幸いです。
2. ランダムフォレストの概要
ランダムフォレストは、権威ある記事では以下のように説明されています。
ランダムフォレストは、機械学習のアルゴリズムであり、分類、回帰、クラスタリングに用いられる。決定木を弱学習器とするアンサンブル学習アルゴリズムであり、この名称は、ランダムサンプリングされたトレーニングデータによって学習した多数の決定木を使用することによる。
フリー百科事典『ウィキペディア(Wikipedia)』
あるいは、
ランダムフォレスト(random forests)は機械学習のアルゴリズムのひとつで、決定木による複数の弱学習器を統合させて汎化能力を向上させる、アンサンブル学習アルゴリズムである
日経リサーチ「ランダムフォレスト」
これらの説明をみると、どうやらランダムフォレストは**「決定木をベースとし、決定木を複数合体させた機械学習アルゴリズム」**のようです。
決定木が複数束ねられていることから、フォレストと呼ばれていることが分かります。
つまり、ランダムフォレストの理解のためにはまず決定木について理解しなければなりません。
以下の記事では、その決定木についての詳説を行っているので、本記事では割愛します。
参考:初心者の初心者による初心者のための決定木
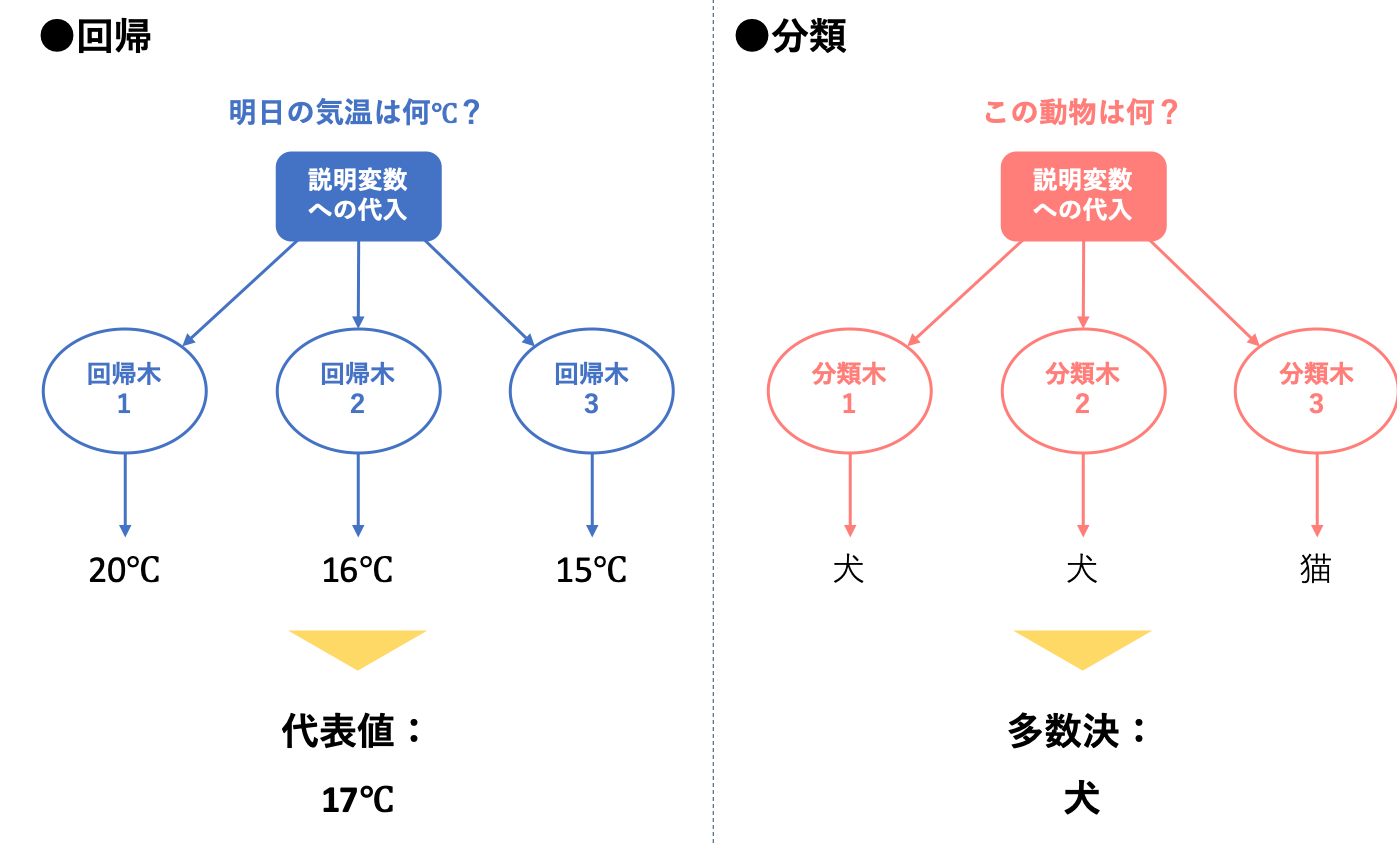
現時点では何となく上図のイメージを持たれているところでしょうか。図左部では代表値と記していますが、多くは平均値を代表値として扱うことが多いようです。
このように、ランムフォレストは決定木を複数組み合わせ、その出力結果を総合して解釈することによって学習を行います。
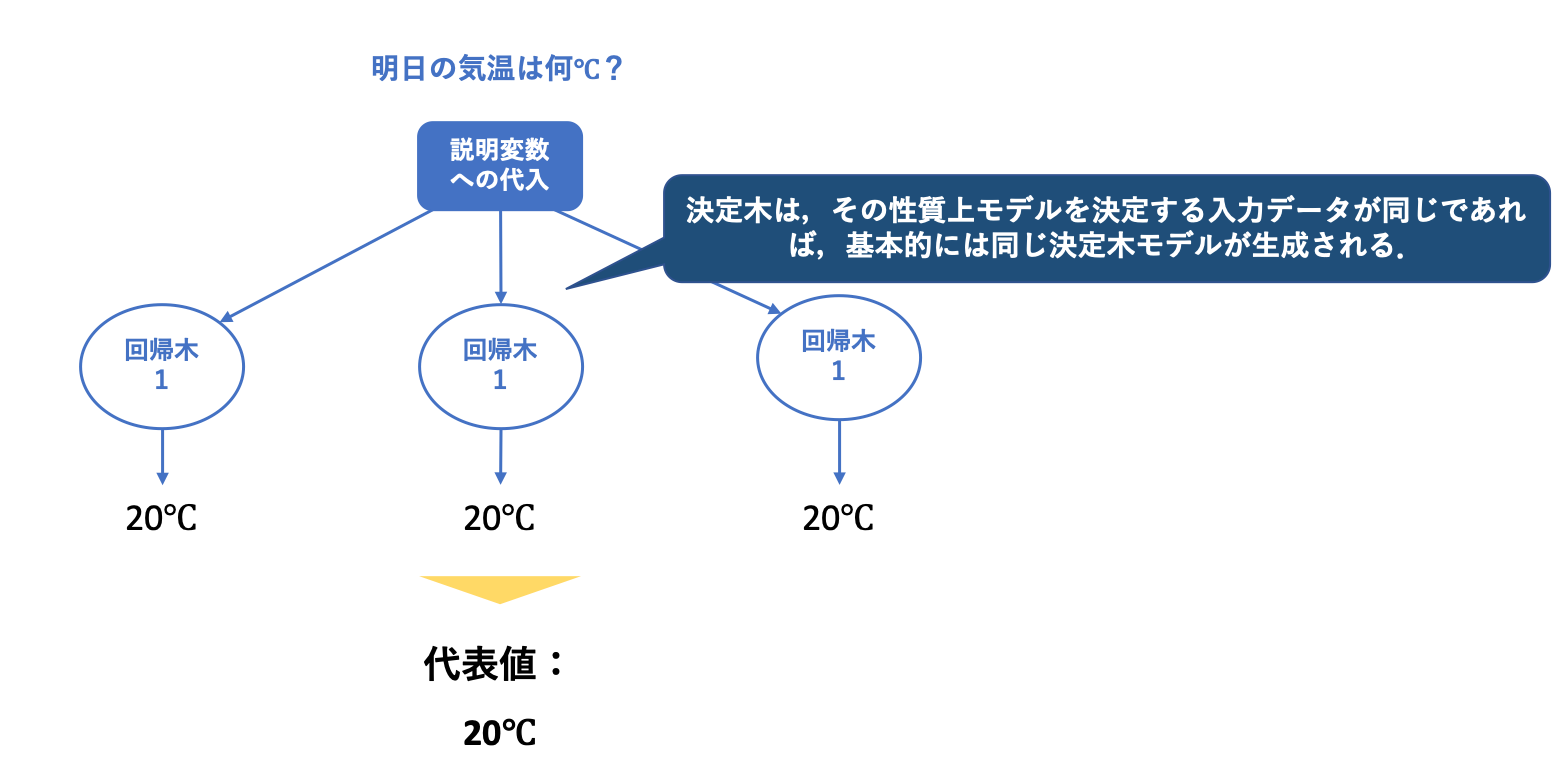
しかし、組み合わせる決定木が同じだと、当然決定木を何本組み合わせたところで同じ出力結果が複数出力されるだけで、平均値による算出や多数決を行っても全く意味がありません。
そして決定木モデルは、そのアルゴリズムの性質上、モデル生成のための入力データが同じ場合は基本的には同じ決定木モデルが生成されてしまいます。(厳密には、不純度の算出の手法を替えることで異なるモデルとすることは可能です)
ですが一番初めの図では、回帰木1, 回帰木2, 回帰木3など異なる決定木モデルが生成されていました。これは複数モデルの組み合わせでモデルの精度を上げるランダムフォレストのまさに狙い通りになっています。
ではランダムフォレストでは、どのように複数パターンの決定木(決定木1, 決定木2, 決定木3...)を生成しているのでしょうか。
この疑問は、ランダムフォレストのアルゴリズムを理解することで解決されます。
3. アルゴリズム
ランダムフォレストのアルゴリズムは、その順で大きく三つから成ります。
1. データの抽出
2. 各データセットに対する決定木モデルの生成
3. 予測のためのデータを入力し、全ての決定木モデルによる結果を統合、1つの予測結果として出力する。
以下では、それぞれのステップについて細かく説明していきます。
3.1. 訓練データからN個のブートストラップデータ集合を抽出
ランダムフォレストでは、このデータ抽出が一つ大きな特徴として挙げられます。
先述したように、ランダムフォレストは決定木を複数組み合わせた学習器なので、その決定木モデルはそれぞれ異なる必要があり、そのためには、そのモデル生成のための教師データを異なるものにする必要があります。
ここで用いられるのが、ブートストラップ法という手法です。
ブートストラップ法
母集団となるデータがあるときに、母集団から重複を許してランダムにいくらかデータを取り出して再標本化をする手法。
具体例としては、
母集団を$X=x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9, x_{10}$としたとき、
- 再標本化を行う回数と,再標本化されたサンプルのサンプルサイズを設定する(例では再標本化を3回,サンプルサイズを5としておく)
- 母集団$X$から重複を許してランダムにサンプリングをする
ことで、
$$X_1 = x_1, x_3, x_3, x_6, x_9$$$$X_2 = x_2, x_2, x_2, x_3, x_7$$$$X_3 = x_2, x_4, x_4, x_5, x_8$$
というブートストラップデータ集合が抽出されます。
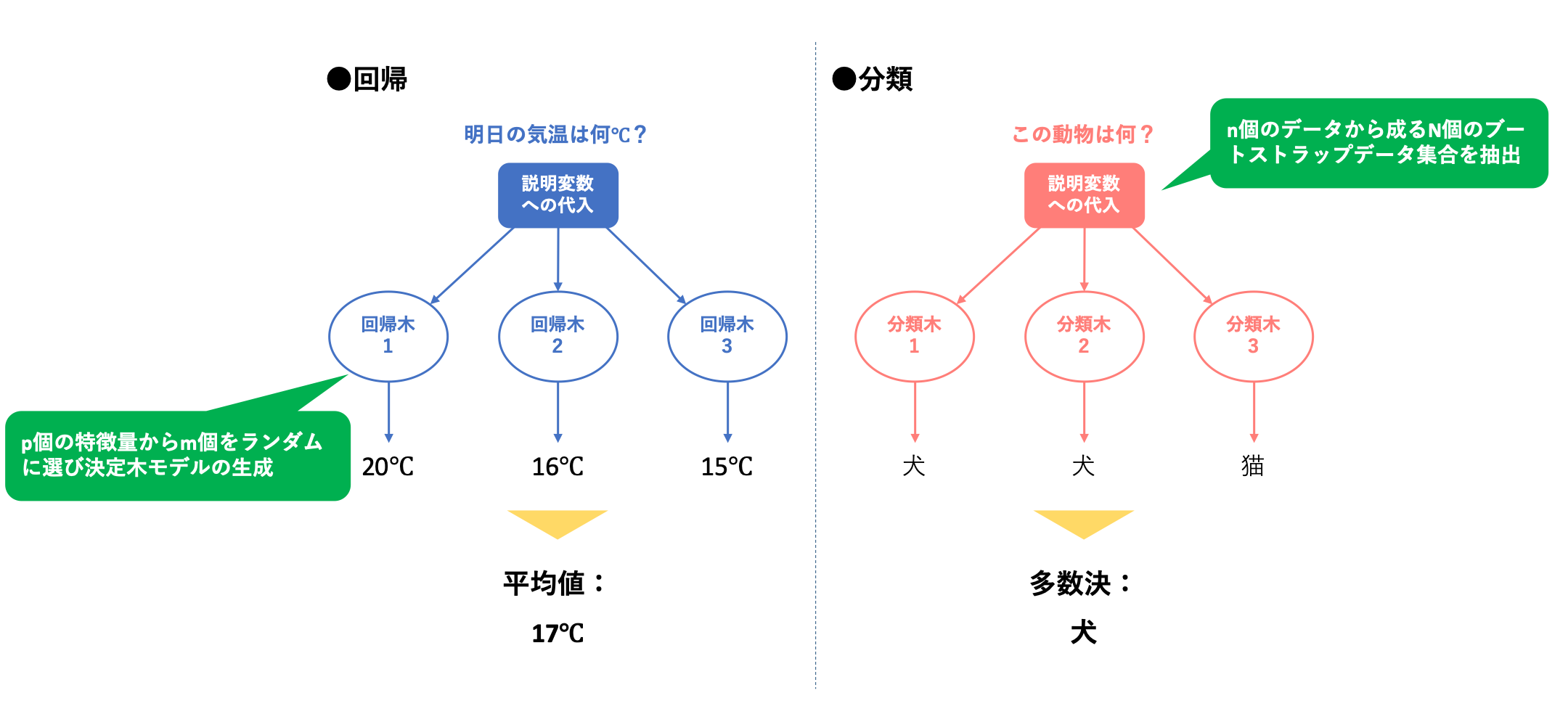
このブートストラップ法を用いて、ランダムフォレストにおいてはまず、**「訓練データから、n個のデータから成るN個のブートストラップデータ集合を抽出」**します。
3.2. 各データセットに対する決定木モデルを生成
続いて、3.1.で抽出したN個のデータ集合に対して、N個の決定木$T^{k}_n(k=1,2,...,N)$を生成する。
ここで非常に重要となるのが、この決定木の生成において、p個の特徴量(説明変数)からm個をランダムに選ぶということです。
- ランダムサンプリングする特徴量の数mはユーザが自由に設定することができますが、一般的には変数の数の正の平方根を取ることが多いようです。
そして、この後決定木$T^{k}_n(k=1,2,...,N)$それぞれに対して学習を行わせるわけなのですが、その決定木アルゴリズムに関しては前記事(初心者の初心者による初心者のための決定木)で説明しているので今回は割愛させて頂きます。(そこが大変笑)
3.3. 全ての決定木モデルによる結果を統合、1つの予測結果として出力
このステップについては簡単な説明に留めますが、決定木$T^{k}_n(k=1,2,...,N)$を介してN個の出力結果が得られるので、回帰の時には平均値を、また分類の時には多数決を行うことによって、一つの出力結果を得ることができます。
3.4. アルゴリズムまとめ
-
訓練データから、n個のデータから成るN個のブートストラップデータ集合を抽出
-
p個の特徴量からm個をランダムに選び、各データセットに対する決定木モデル$T^{k}_n(k=1,2,...,N)$の生成
-
予測のためのデータを入力し、全ての決定木モデルによる結果を統合、1つの予測結果として出力する。(回帰の時は平均値、分類の時は多数決)
4. 特徴
ここで最後に、学習アルゴリズムとしてのランダムフォレストの長所/短所を整理します。
長所
- 各決定木を作成する計算は並列化できるので、高速な計算が可能
- 特徴量のスケーリングが必要ない(SVMなどの分類手法では必要になる)
- 考慮するパラメータが少ない
- どの特徴量が重要かを知ることができる
短所
- 複雑なデータではSVMなどの分類手法に比べて汎化性能が下がる
- ノイズが多すぎるデータでは過学習してしまう
- 決定木よりも計算が複雑
5. 参考記事
初心者の初心者による初心者のための決定木
ブートストラップサンプリング(Bootstrap Sampling)法とそのscikit-learnを用いた実行
ランダムフォレストとは?PythonとRで実装してみよう!
ランダムフォレストの概要を大雑把に解説
【機械学習】ランダムフォレストについて メモ
ランダムフォレストの理論と重要な特徴量の選定
【機械学習】ランダムフォレスト