機械学習初心者でも、決定木(Decision Tree)について理解しなければならない日がいつか来る。なので初心者代表の私が、決定木について初心者なりに分かりにくいところなどを含め解釈したものをまとめてみました。
加筆修正のコメント等あれば、遠慮なく教えてください。
そして、タイトルが非常に類似している以下の記事について、本記事も大いに参考にさせて頂いているので、よろしければご参照ください。
[入門]初心者の初心者による初心者のための決定木分析
1. 本記事の目的
本記事では、決定木を実装する上で施されている工夫について理論的な説明を詳しくしていきます。
決定木は他の機械学習手法と比較して分かり易いと言われてますが、ランダムフォレストを理解するうえで必須になるので、自己復習がてらまとめようと思います。
2. 機械学習手法の中での決定木
ここでは、決定木の中身について詳述する前に、他の機械学習手法と比較したときの決定木の立ち位置について述べていきます。
2.1. 決定木の使い所
以下に、決定木分析はどの状況下で行うことが適切かを表したチートシートを示します。
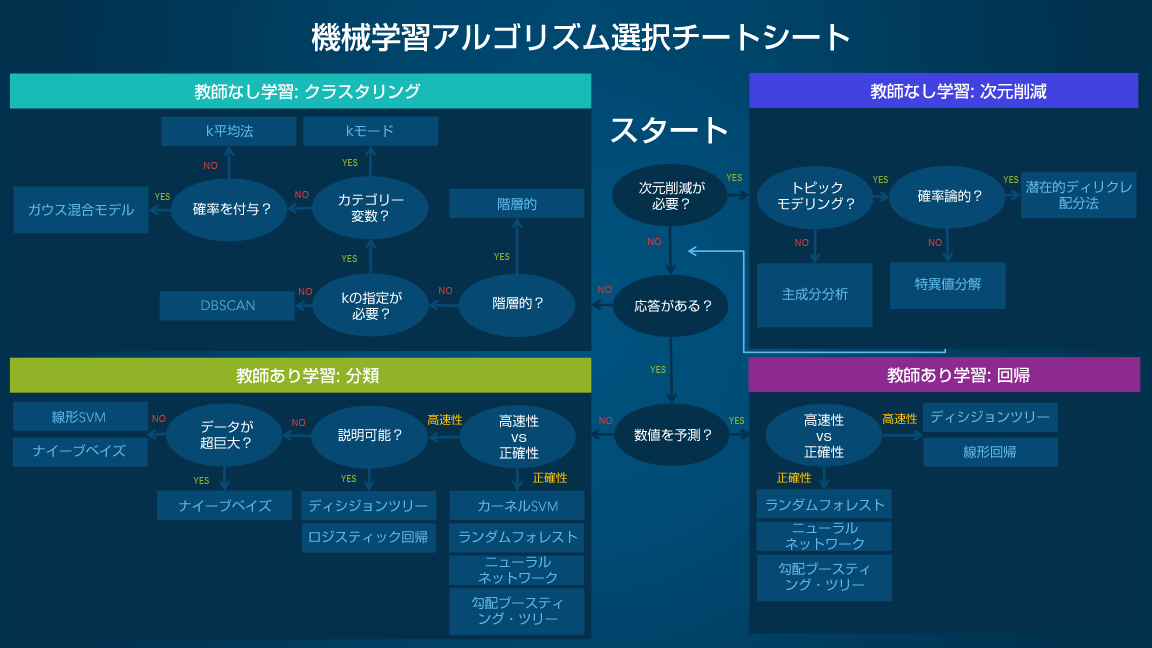
参照:機械学習アルゴリズム選択ガイド
上表をみると、複数ある機械学習手法の中で決定木(ディシジョンツリー)を選択することが推奨される状況は、
**「次元削減が必要ではなく、元データに応答があり、回帰/分類どちらにおいても高速性を重視し、説明可能な結果を得たいとき」**となります。
ここで、元データの応答の有無とは、おそらく元データに教師ラベルがあらかじめ付与されているかどうかだと考えられます。
2.2. 決定木の長所と短所
ここで、決定木の長所/短所を整理します。ただ以下は引用であり、いまいち自分では腑に落ちない部分があるため、そこに関しては所感を述べています。詳しい方によるご指摘をお待ちしています!
長所
-
結果の解釈が容易である:分類過程をツリーの出力によって可視化できます
-
説明変数/目的変数共に名義尺度から間隔尺度まで様々扱える:質的データから量的データまで様々扱えます
-
外れ値に対して頑健←分類問題自体がそもそもそうではないか?他の学習器と比較して相対的に頑健な理由がよく分からない
-
データの分布の型を問わない:決定木分析では、「データを分割する指標」として特徴量を使うので、データの前処理(スケーリング等)に伴う負担がかなり軽減されます。ツリーの分岐条件において、決定木は複数次元での比較を行わないため、ニューラルネット等と異なりデータを正規化する必要がありません。(おそらく)
短所
-
性能自体はそこまで高くはない:SVMの方が良いと言われています
-
過学習を起こしやすい:木が過度に分岐することが多いため、学習設定や刈り込みが必要となります
-
データが少し変わるだけで全く異なるツリーが生成されることがある
-
線形性のあるデータには適していない
-
XOR(線形分離不能)には適用できない←これも曖昧のようです。すみません><
3. 決定木(Decision Tree)の基本
3.1. 決定木とは
決定木とは、**「教師データをもとにある数理的基準にのっとってIF-ELIF-ELIF...-ELSE THEN文の形で表せるように分岐を作って分類するモデル」**と一言で表すことができます。
そして決定木とは、分類木という分類モデルと回帰木という回帰モデルを合わせたモデルの総称を指すようです。
やりたいことが分類であれば分類木を使い、やりたいことが数値予測であれば回帰木を使います。
ただ僕の勝手な印象ですが、回帰よりは分類のために用いられることが多いのではないかなと思います。後述する決定木作成のアルゴリズムを見ても分類向きなような気がしますが、その理由については後述します。
では、いよいよ本題である決定木アルゴリズムの中身について見ていくことにしますが、まず概観としての大枠を示し、そのあとにそれぞれ細かい部分について見ていくことにします。
3.2. 決定木アルゴリズムの概観
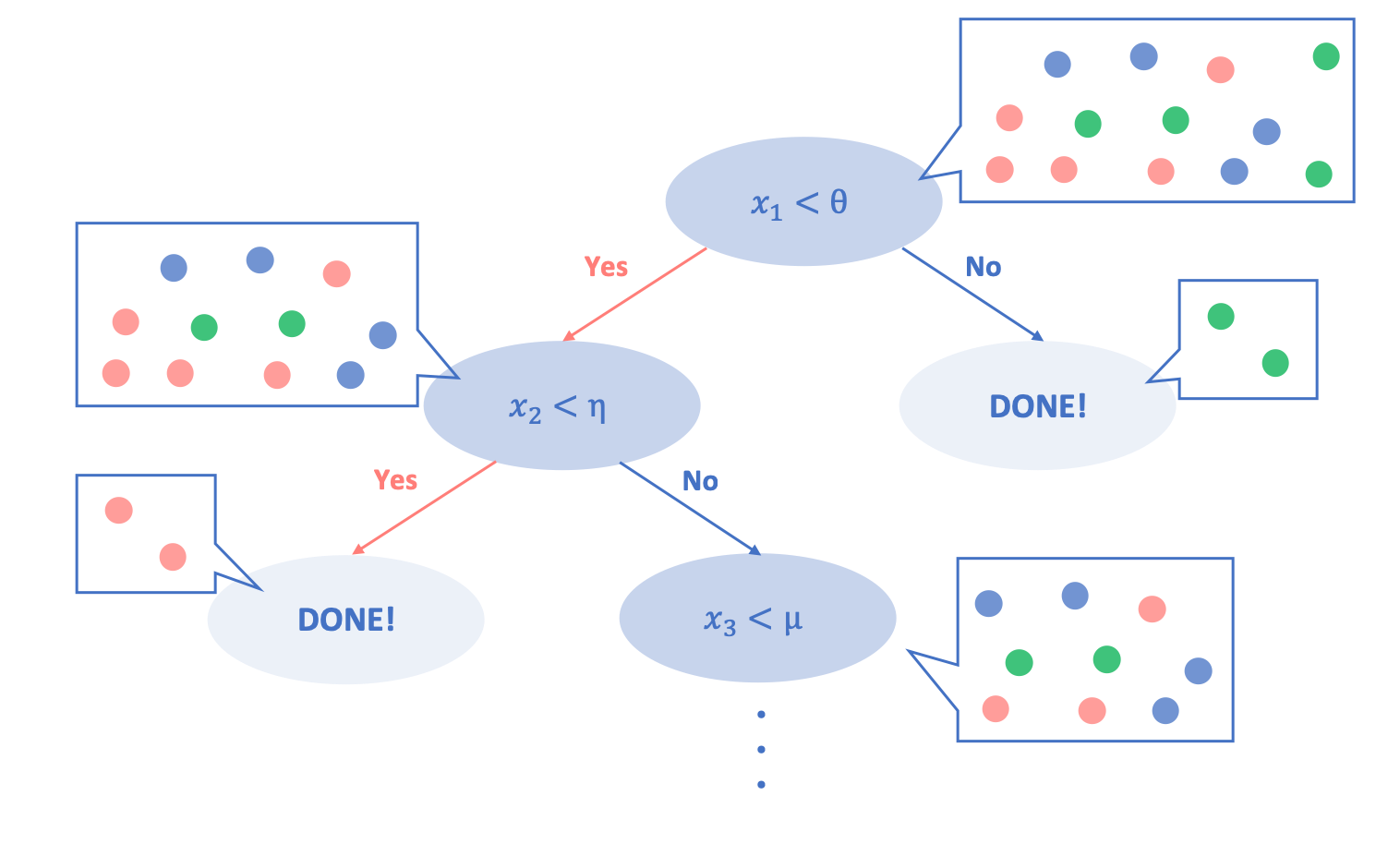
以下の図は、決定木分析がどのようになされるかを簡単に示したものです。
学習ステップとしては、次のようなフローになります。
1. まずこのツリーを構築するために、学習データがすべてルートノード(ツリーの大元)に集められます。
2. そして、教師ラベルをもったそのデータが「一つの説明変数の元で最適に分割される」ような説明変数を一つ選び、その説明変数における閾値を設定することで、元データを分割します。
3. 分割後、またそれぞれのノードにおいて分割を行います
4. ステップ2,3をそれぞれのノードにおいて、「最終的に最適に分割される」まで繰り返します。
ここで問題となるのは、**「一つの説明変数の元で最適に分割される」, 「最終的に最適に分割される」ことがどのようになされるかということに関してですが、ここでポイントになるのが「不純度」(purity)**という概念です。
**「最適な分割」は、このノード内の「不純度の減少幅を最も大きくなる」ような説明変数とその閾値を選び出し、その条件に従って行われます。**つまり、「個々の分岐に来るごとにできるだけその1回で『集団としてのバラバラさ=不純度』が大幅に少なくなるようにする」ことで、分岐が進めば進むほどサンプルが純度が高く綺麗に分類されていくように、木の枝を茂らせていく(条件を変えながら分岐を増やしていく)というのがアルゴリズムの基本です。そしてこれを、全ての分岐ノードが打ち切り基準に達するまで繰り返す。これが決定木の具体的なアルゴリズムとなります。
さて、それではその「不純度」がどのように数値化されるかですが、指標としては主に二つ、**「エントロピー」, 「ジニ係数」**が用いられています。以下では、その二つの指標それぞれについて説明します。
3.3. 不純度指標としてのエントロピー
「エントロピー」とは一言で言えば物事の乱雑さを測る指標のことで、主に熱力学や情報理論の中で用いられます。Googleで検索すると、「原子的排列および運動状態の混沌(こんとん)性・不規則性の程度を表す量」と定義づけされていることが分かります。
そして決定木分析においては、一つのノードにおける、分割前と分割後のエントロピーの減少幅が最大になることを目指します。
情報理論分野では、エントロピーは平均情報量とも呼ばれており、通常以下の式で表されます。
\begin{align}
H(P) &= E_P\left[\log\frac{1}{P(\omega)}\right] = \sum_{\omega\in\Omega}^{}P(\omega)\log\frac{1}{P(\omega)}\\
&= -\sum_{\omega\in\Omega}^{}P(\omega)\log{P(\omega)}\end{align}
ここで、$H(P)$は、確率$P(\omega)$で発生する事象を伝えるのに要する情報量$(\log\frac{1}{P(\omega)})$の全体での期待値を示しています。エントロピーについてより詳しく知りたい方は、以下の記事が参考になるかと思います。
雑記: 交差エントロピーって何
そして、このエントロピーの式を決定木において用いられる式に置き換えてみると以下のようになります。
I_{H}(t) = -\sum_{i=1}^{c}p(i|t)\log_2p(i|t)\\
ただし、p(i|t) = \frac{n_i}{N}
ここで、$c$は目的変数のクラス数、$t$は現在のノード、$N$はノード$t$でのトレーニングデータのサンプル数、$n_i$はノード$t$でクラス$i$に属するトレーニングデータの数を示しています。
例えば以下にあげる先ほどの図を用いれば、
左側のノードのエントロピー
$= -\sum_{i=1}^{1}\frac{n_i}{N}\log\frac{n_i}{N} = \frac{2}{2}\log\frac{2}{2} = 0$
右側のノードのエントロピー
$= -\sum_{i=1}^{3}\frac{n_i}{N}\log\frac{n_i}{N} = \frac{2}{9}\log\frac{2}{9}+\frac{3}{9}\log\frac{3}{9}+\frac{4}{9}\log\frac{4}{9} = …$
となります。
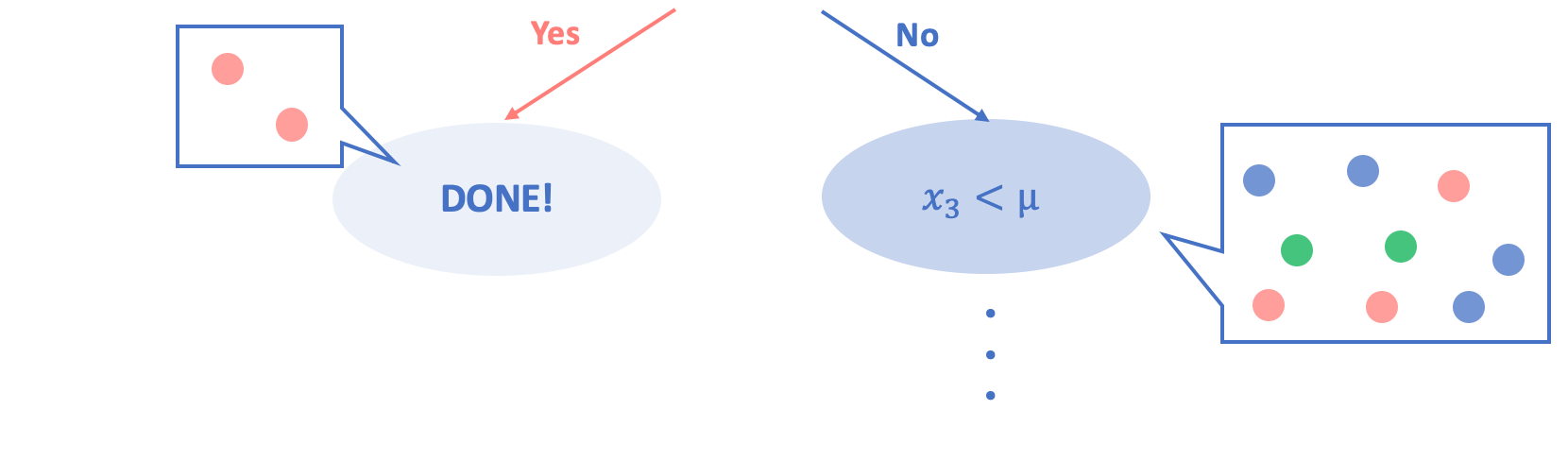
つまり、不純度が最も低い、すなわちノード内のサンプルが全て同じクラスに属している場合はそのエントロピーは0となり、不純度が高い、すなわちノード内のサンプルが全て異なるクラスに属している場合はそのエントロピーの値が大きくなります。
このことから、エントロピーを用いてノードの不純度を数値化できることが伺えます。そして、この分割指標を用いて決定木を構築していくアルゴリズムがC4.5です。
3.4. 不純度指標としてのジニ係数
さて、上項では不純度を数値化するための指標としてエントロピーを紹介しましたが、もう一つ一般的に用いられている不純度指標として「ジニ係数」があります。以下それについて説明します。
ジニ係数は、もともと計量経済学の分野で社会における所得などの分布の均等度合いを示す指標であり、国民経済計算等に用いられるもののようです。ジニ係数の値は0から1の間をとり、係数が0に近づくほど所得格差が小さく、1に近づくほど所得格差が拡大していることを示します。
そしてジニ係数は決定木においては以下の式で表されます。
\begin{align}
I_{G}(t) &= \sum_{i\neq{j}}p(i|t)p(j|t) = \sum_{i=1}^{c}p(i|t)(1-p(i|t))\\
&= 1 - \sum_{i=1}^{c}{p(i|t)}^2\end{align}\\
ただし、p(i|t) = \frac{n_i}{N}
ここで、$c$は目的変数のクラス数、$t$は現在のノード、$N$はノード$t$でのトレーニングデータのサンプル数、$n_i$はノード$t$でクラス$i$に属するトレーニングデータの数を示しています。
先ほどの図をもう一度用いれば、それぞれのジニ係数は、
左側のノードのジニ係数
$= 1 - \sum_{i=1}^{1}\left(\frac{N}{N}\right)^{2} = 0$
右側のノードのジニ係数
$= 1 - \sum_{i=1}^{3}\left(\frac{n_i}{N}\right)^{2} = 1-\left[\left(\frac{2}{9}\right)^2+\left(\frac{3}{9}\right)^2+\left(\frac{4}{9}\right)^2\right]$
となります。

つまり、不純度が最も低い、すなわちノード内のサンプルが全て同じクラスに属している場合はそのジニ係数は0となり、不純度が高い、すなわちノード内のサンプルが全て異なるクラスに属している場合はそのジニ係数の値が大きくなり、その値は1に漸近します。
このことから、ジニ係数を用いてノードの不純度を数値化できることが伺えます。そして、この分割指標を用いて決定木を構築していくアルゴリズムがCARTです。
3.5. 情報利得
さて、ここまでで不純度を数値化するための指標として**「エントロピー」, 「ジニ係数」**の二つが一般的に用いられていることが分かりました。
では、『「最適な分割」はノード内の「不純度の減少幅を最も大きくなる」ような説明変数とその閾値を選び出し、その条件に従って行われる』と述べましたが、では具体的に不純度の減少幅はどのようにして求められるのでしょうか。
これについては、**「情報利得」**という概念を用いることによって算出します。「情報利得」とは、データ分割の前後を比較してどれだけ綺麗にデータを分割できたかを数値化したものです。
そして、その情報利得は以下の式で表されます。
= 分割前の不純度 - $\sum$(重み$\times$不純度)
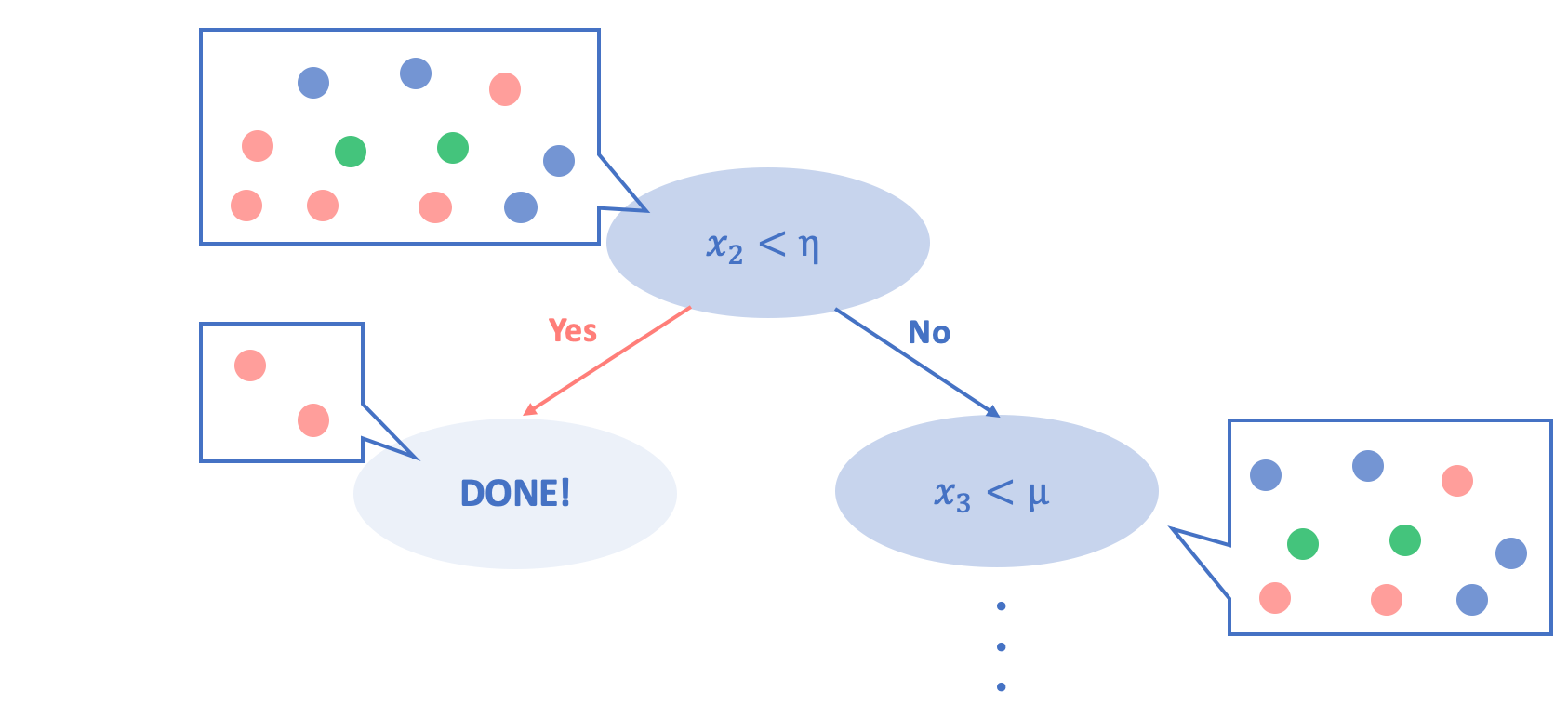
既出の図に分割前のデータを加えた上図を見てみましょう。
不純度の算出にジニ係数を用いた場合、
分割前の不純度
$= 1 - \sum_{i=1}^{3}\left(\frac{n_i}{N}\right)^{2} = 1-\left[\left(\frac{4}{11}\right)^2+\left(\frac{3}{11}\right)^2+\left(\frac{4}{11}\right)^2\right]$
分割後の不純度
$= \sum(重み\times不純度) = \frac{2}{11}\times0 + \frac{9}{11}\times(1-\left[\left(\frac{2}{9}\right)^2+\left(\frac{3}{9}\right)^2+\left(\frac{4}{9}\right)^2\right])$
となります。そして、決定木は分割前と分割後の不純度の差を情報利得として算出し、その情報利得が最大となるような分割を行います。
数式で表すと、以下のようになるでしょうか。(雑でごめんなさい)
$$\Delta I = max (I_{before} - \sum_{i=1}^{b} w_{i}*I_{i, after})$$
※一般的な感覚としては、(分割後ー分割前)の絶対値を最大化させるという解釈をしやすいですが、不純度の値が小さい方がいいという性質上、max(分割前ー分割後)を求めることと同義になります。
4. 決定木の工夫
さて、以上が決定木分析の基本アルゴリズムとなります。しかし、いよいよこの手法を実データに適用しようとしたとき、決定木には「過学習(オーバーフィッティング)を起こしやすい」という難点がありました。そこで、決定木分析に欠落している「汎化性能」を得るためには、「剪定」をすることによって木の深さを制限する必要があります。
もし剪定をせずに木の深さに制限をかけなかった場合、「モデル作成に利用したデータ」に対して過剰に適合してしまい、「新しいデータ」に対する精度が低くなってしまうからです。 また、決定木分析をする目的として「なんとなくデータが分割されていく過程を目視したい」といった場合もありますが、そのような際にも木があまりにも深いと理解が難しくなってしまいます。
決定木分析についてざっくりまとめ_理論編
4.1. 正則化項
ここでは正則化項についての詳細な説明は省略しますが、正則化項とは目的関数の中に組み込むサブ的な項であり、過学習を防ぐために加えられる追加項のことです。
決定木においては、木が細かく複雑になりすぎる、すなわち終端ノード(最終的に分割され切った後のノード)の数が多ければ多いほど過学習になっている可能性が高いと考えて、正則化項は一般的に、
$$\alpha|T|$$
と表されます。ただし、$\alpha$は正則パラメーター, Tは終端ノードの数を表します。
なのでこれを基本的な目的関数に加え、それぞれの情報利得を計算していくことになります。
4.2. αの決定
ではその正則パラメーター$\alpha$はどのように求められるのでしょうか。もし、直観的に分かりやすくするために小さい木を求める場合はαを大きく、学習データにおける精度を上げたい場合はαを小さく設定すればよいです。
しかし一般的には、交差検証法(cross validation)によって最適と思われるαを定めることが多いようです。
補足: Cross Validationとは
学習に使ったデータに対しての当てはまりではなく、予測の際の当てはまりでどれだけ信頼できるかを求めるための手法の1つとなります。 機械学習などでは、未知のデータの予測がどれだけ行えるかが重要となるため、データの一部を学習には使わずに作成されたモデルに対する予測がどの程度うまくいかに利用したりします。 Cross Validationはデータが少ないときなどに効果的なやり方で、データ全体をn個に分割してn-1個を学習に、残りの1個を評価に用いるというのをn回繰り返す手法になります。
決定木モデルを作る #alteryx #03 | Alteryx Advent Calendar 2016
最後の方少し力尽きた感が出てしまいましたが、ランダムフォレストを完璧に理解するための決定木の理解だったので、実装などについては割愛します!
読んでくれた方はありがとうございました。次回はランダムフォレストについてゴリゴリ書いていこうと思います。
5. 参考文献
[入門]初心者の初心者による初心者のための決定木分析
パッケージユーザーのための機械学習(1):決定木
決定木による学習
決定木モデルを作る #alteryx #03 | Alteryx Advent Calendar 2016
複雑になりがちな決定木を汎用的に変身!剪定の考え方について