ランダムフォレストという概念についてのメモです。
ど素人によるまとめなので誤りなどあるかもしれません。その時は指摘していただけると嬉しいです。
ランダムフォレストとは
ランダムフォレスト(英: random forest, randomized trees)は、2001年に Leo Breiman によって提案された機械学習のアルゴリズムであり、分類、回帰、クラスタリングに用いられる。決定木を弱学習器とする集団学習アルゴリズムであり、この名称は、ランダムサンプリングされたトレーニングデータによって学習した多数の決定木を使用することによる。対象によっては、同じく集団学習を用いるブースティングよりも有効とされる。(Wikipedia)
決定木が複数を束ねるところから、「フォレスト」と呼ばれる。
ブートストラップサンプリングにより標本データ群から無作為に抽出されたデータ・特徴量から決定木を作成し、作成された決定木を多数決的に結合することで適切なモデルを生成するアルゴリズム。
回帰・分類の両方の分析に用いることができ、それぞれ回帰木・分類木と呼ぶ。
バギングが無作為のデータ抽出(ブートストラップサンプリング)のみを行うのに対して、ランダムフォレストではそれに加えて特徴量もランダムに抽出する点で、バギングの応用的立ち位置にある。
ランダムフォレストに関する諸概念
決定木
機械学習の分野においては決定木は予測モデルであり、ある事項に対する観察結果から、その事項の目標値に関する結論を導く。内部節点は変数に対応し、子節点への枝はその変数の取り得る値を示す。 葉(端点)は、根(root)からの経路によって表される変数値に対して、目的変数の予測値を表す。
データから決定木を作る機械学習の手法のことを決定木学習 (英: decision tree learning)、あるいはくだけた言い方では単に決定木と呼ぶ。(Wikipedia)
どの特徴量を元に分割すると良い分け方ができるか、を探すアルゴリズム。
ブートストラップサンプリング
サンプル集合 X={x_i}^N から,重複を許してサンプリングして新たなサンプル集合 X' を作る方法
(引用:http://ibisforest.org/index.php?ブートストラップ)
GradientBoosting,AdarBoosting,XgBoostingなど。
標本データから無作為にデータを抽出し、標本データと同じサイズのデータを作る(リサンプリング)こと。
バギング
ブートストラップサンプリングを繰り返して生成した判別器を合成して,より判別精度の高い判別器を生成する方法.
(引用:http://ibisforest.org/index.php?バギング)
ブートストラップサンプリングにより生成されたモデル(弱識別器)を多数決的に結合し、より優れたモデルを生成する方法。
一つの決定木からモデルを生成するよりも高い精度のモデルを生み出すことができる。
ランダムフォレストの流れ
ランダムフォレストの実践は以下のような流れを取る。
- 1.データの抽出
- 2.決定木の成長
- 3.算出された決定木群から多数決によって優れた決定木を生成
1.データの抽出
対象の標本データ群から、決定木作成のためにデータを抽出する。
一つの標本データから復元抽出を繰り返すことで大量の標本データを生成する。
(ブートストラップサンプリング)
2.決定木の生成
生成された大量の標本データそれぞれから、決定木を生成する。
作成した標本データと同じ数だけの決定木が作成される。
3.優れた決定木の生成
作成された大量の決定木を多数決的に結合し、優れた決定木(判別機)を生成する。
プログラムによる試行
回帰木
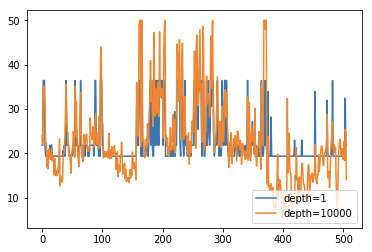
ランダムフォレストによる回帰について。
設定する決定木の深さにより、粒度が変化するのが見て取れる。
深いほど粒度が小さくなるので過学習してしまいやすい。
import pandas as pd
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
from matplotlib import pyplot as plt
dataset = load_boston()
data_x = pd.DataFrame(dataset.data, columns=dataset.feature_names)
data_y = pd.DataFrame(dataset.target, columns=['target']).as_matrix().ravel()
# ランダムフォレストの生成および訓練
# モデル1は決定木の深さを1に、モデル2は深さを10000に設定
rf1 = RandomForestRegressor(max_depth=1)
rf2 = RandomForestRegressor(max_depth=10000)
rf1.fit(data_x, data_y)
rf2.fit(data_x, data_y)
result1 = rf1.predict(data_x)
result2 = rf2.predict(data_x)
# 生成したモデルが判断した特徴量の重要性について。
print('深さ 1 の時の各特徴量の重要性')
print(rf1.feature_importances_)
print('深さ 10000 の時の各特徴量の重要性')
print(rf2.feature_importances_)
# 出力結果
深さ 1 の時の各特徴量の重要性
[ 0. 0. 0. 0. 0. 0.5 0. 0. 0. 0. 0. 0. 0.5]
深さ 10000 の時の各特徴量の重要性
[ 0.03435951 0.00117056 0.00528091 0.00051407 0.02940801 0.36078732
0.01256347 0.06518549 0.00908767 0.01362662 0.01148436 0.01460661
0.44192541]
plt.plot(result1,label="depth=1")
plt.plot(result2,label="depth=10000")
plt.legend(loc="lower right")
plt.show()
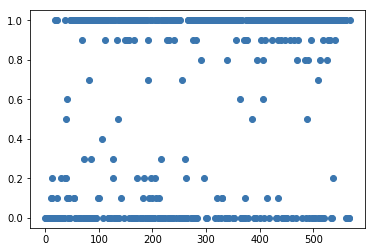
分類木
正解データが2値であるデータを読み込ませると分類となります(多値でも)
from sklearn.datasets import load_breast_cancer
dataset = load_breast_cancer()
data_x = pd.DataFrame(dataset.data,columns=dataset.feature_names)
data_y = pd.DataFrame(dataset.target,columns=['target']).as_matrix().ravel()
model = RandomForestRegressor()
model.fit(data_x,data_y)
print('モデルの決定係数')
print(model.score(data_x,data_y))
print('各特徴量の重要性')
print(model.feature_importances_)
# 出力結果
モデルの決定係数
0.966769991015
各特徴量の重要性
[ 0.00494909 0.01918329 0.0010003 0.00375017 0.00574955 0.00173082
0.00464166 0.08584162 0.00121563 0.00397705 0.0014529 0.00079244
0.00189821 0.01166476 0.00168054 0.0006904 0.00399333 0.00573283
0.00187071 0.00322677 0.08570888 0.0346185 0.35983106 0.10812259
0.00998039 0.00295977 0.00167323 0.22573015 0.00179003 0.00454332]
plt.plot(model.predict(data_x), 'o')
plt.show()
終わりに
ちょっと説明が雑になってしまったので、後ほど編集し直します。
以上。