<機械学習を目的関数から考えてみる>
こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、機械学習において重要な位置を占めます目的関数について考えてみます。
1. はじめに
機械学習を適用するとき、一般にデータを用いてモデルのパラメータ値を決める学習と呼ばれる手続きを行います。このとき、その多くは、目的関数と呼ばれるデータの値を変数として持つ関数の値を最小化あるいは最大化することで、パラメータ値を決めます。目的関数にはさまざまな種類があり、適用する機械学習に応じて変わります。本記事では、さまざまな目的関数とそれに対応する機械学習を紹介することで、機械学習を目的関数から考えてみたいと思います。
2. 機械学習の分類と損失関数の役割
機械学習は、教師あり学習、教師なし学習、強化学習の3つに分類されることが多いです。いずれも、なんらかの形で得たデータを用いてモデルのパラメータ値を決定する学習と呼ばれるプロセスが存在します。
教師あり学習もしくは教師なし学習の一部では、基本的にはモデルの出力と所望の出力との差違が小さくなるようにモデルのパラメータ値を決めます。このようなパラメータ値を決めるために、目的関数と呼ばれる関数を用いて、当該関数の値を最小化あるいは最大化することで、モデルの出力と所望の出力との差違を小さくするようなパラメータ値を得ます。目的関数には、さまざまな形がありますが、学習に用いた目的関数は、そのモデルのパラメータ値がどのような考え方で決められたのかを表しており、その役割は重要です。本記事では、次の目的関数をご紹介したいと思います。
・二乗誤差の和
・尤度
・ヒンジ損失の和
・ε-不感損失の和
・情報利得
・交差エントロピー
3. さまざまな損失関数
3-1. 二乗誤差の和(二乗和誤差)
二乗誤差 $l_s^k$ を(1)式に示します。$k$は、データ番号(レコード番号)です。
$$
l_s^k=(\hat{y}_k-y_k)^2\hspace{1cm}・・・(1)\\
\hat{y}_k:モデルの出力\\
y_k:所望の出力
$$
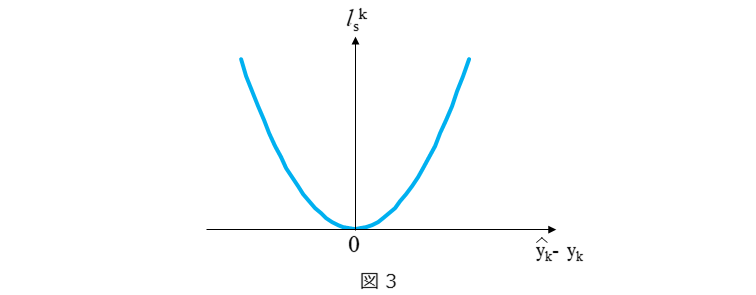
モデルの出力と所望の出力との差違として、モデルの出力と所望の出力の差の二乗を用います。二乗誤差 $l_s^k$ のイメージを図3に示します。モデルの出力と所望の出力の誤差が大きくなるほど、二乗誤差 $l_s^k$ は急激に大きくなっていくことが分かります。
各データで演算される二乗誤差 $l_s^k$ をすべて足した二乗和誤差が最小となるように、モデルのパラメータ値を決めます。二乗和誤差 $J_s$ を(2)式に示します。
$$
J_s=\sum_{k=1}^{N}l_s^k\hspace{1cm}・・・(2)\
$$
上述しましたように、モデルの出力と所望の出力の誤差が大きくなると、二乗誤差 $l_s^k$ は急激に大きくなりますので、このとき、 二乗和誤差 $J_s$ の値も応分大きくなります。$J_s$をできるだけ小さくするようにパラメータ値が学習されますので、著しい外れ値がある場合、その影響で $J_s$ の値が大きくなり、その外れ値による差違を優先的に小さくするようにパラメータ値が学習されることになります。このことは、モデルの特性が、その外れ値に引きずられやすくなることを意味しています。
二乗和誤差を最小化するようにパラメータ値を決める方法が最小二乗法です。特に、パラメータに対して線形なモデルであるとき、正規方程式と呼ばれる方程式を解くことで、最小二乗解が得られます。このとき、二乗和誤差はパラメータ値に対して下に凸になりますので、大域最適解が保証されます。また、パラメータに対して線形、非線形に関わらず、全領域で微分可能ですので勾配を用いた最適化が可能です。
この二乗和誤差を目的関数として用いるモデルとして、線形回帰、深層学習などがあります。なお、前者は全線形モデル、後者は非線形モデルです。二乗誤差は、上述のように、外れ値の影響を受けやすい特性はあるもののモデルの出力と所望の出力の誤差が大きいほど、その値も大きくなるので予測精度を表現する指標としては自然です。誤差の絶対値を用いる方が自然に思う方もいらっしゃるかもしれませんが、上述のように、二乗誤差にすることで、勾配を用いた最適化が可能なことが絶対値誤差との違いで、計算上のメリットと言えます。
あくまでも私の個人的な見解ですが、二乗和誤差は、もっともポピュラー(?)な、目的関数ではないでしょうか。
3-2. 尤度
確率密度関数 $f(y_k;\theta)$ について考えます。 $y_k$ 観測値であり、$\theta$ は確率分布を決めるパラメータです(たとえば、正規分布の平均値、分散に当たります)。$f$ は、なんらかの確率分布を表しますが、パラメータ $\theta$ の値はすでに決まっていて、確率変数の観測値 $y_k$ が発生する確率を与えます。このとき、(3)式で与えられる $J_l(=L(\theta;y_k))$ を尤度と言います。
$$
J_l=L(\theta;y_k)=\prod_{k=1}^{N}f(y_k;\theta)\hspace{1cm}・・・(3)\
$$
(3)式の意味を考えます。$y_1$~$y_N$ までのデータが得られたとき、それをもっともうまく説明できるパラメータ $\theta$ を求めることを考えます。つまり、実際に起きたことが、パラメータ $\theta$ を求めるためのもっとも有力な情報であるとの立場を取ります。このとき、$y_1$~$y_N$ が発生した確率の積である $f(y_1;\theta)\times f(y_2;\theta)\times・・・ \times f(y_N;\theta)$ がもっとも高くなるように $\theta$ の値を決めれば良いことになります。前節でご紹介しました二乗和誤差 $J_s$ では、各データで演算される二乗誤差 $l_s^k$ の和でしたが、尤度 $J_l$ は $f$ のかけ算になっています。これは、上記の理由からです。なお、尤度 $J_l$ は、パラメータ $\theta$ の関数ですので、このとき尤度を尤度関数とも呼びます。
この $J_l$ を最大化するような $\hat{\theta}$ を求めます。上述しましたように、これは、ある仮定したモデル(確率密度関数)$f(y_k;\theta)$ に、実際に観測した $y_k$ の分布がもっとも当てはまるように $\hat{\theta}$ の値を決めることを意味します。当てはまり度合いが高いほど、$J_l$ は高くなります。もう少し考えてみますと、このことは、観測値 $y_k$ が従う真の分布から得られる出力 $y$と、仮定した分布から得られる出力 $\hat{y}$ の差がもっとも小さくなるように、$\theta$ の値を決めていると言え、所望の出力(真の出力)$y$ とモデルの出力 $\hat{y}$ との差違を小さくするように、パラメータ値を決める手法とも解釈できます。
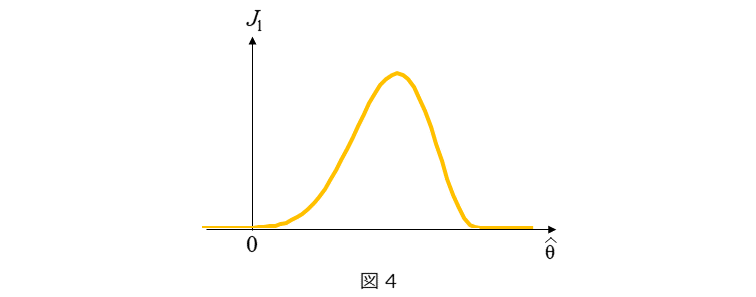
尤度 $J_l$ のイメージを図4に示します。二乗和誤差では、パラメータ値に対して下に凸になりますが、 尤度 $J_l$ はパラメータ値 $\hat{\theta}$ に対して上に凸になっていることがわかります。また $J_l$ が取る範囲は、0≦ $J_l$ ≦1となります。
$J_l$ を最大化するようにパラメータ値を決める方法が最尤推定法です。実際には、尤度関数ではなく、数学的に扱いやすい対数化した対数尤度を最大化することでパラメータ値を決定します。対数尤度にしますと、(3)式の右辺の $f$ のかけ算が、$f$ の対数の足し算になりますので、微分しやすく扱いやすくなります(この形になりますと、二乗和誤差と同じく積算の形になりますね)。なお、対数尤度も同じく、パラメータ $\hat{\theta}$ に対して上に凸になりますが、対数尤度が取り得る範囲は、$-\infty$ ≦(対数尤度)≦ 0となり、最大値は0となります。対数尤度も上に凸ですので、大域最適解が保証されます。なお、真の分布として正規分布を仮定しますと、求めたいパラメータ $\theta$ は正規分布の母数となりますが、このとき、最小二乗法で求められるパラメータ $\hat{\theta}_s$ の値と最尤推定法で求められるパラメータ $\hat{\theta}_l$ の 値は一致します。
この尤度 $J_l$ を目的関数として用いるモデルとして、ロジスティック回帰があります。ロジスティック回帰は疾病などの発生確率を求めるモデルですので、尤度を目的関数とすると相性が良いと言えます。ロジスティック回帰については、下記の記事でより詳しく御説明しておりますので、適宜、ご参考下さい。
3-3. ヒンジ損失の和
ヒンジ損失 $l_h^k$ を(4)式に示します。
$$
l_h^k=max\{\ 0, 1 - \hat{y}_k\cdot y_k\ \} \hspace{1cm}・・・(4)
$$
ヒンジ損失は聞いたことがない、という方もいらっしゃるかもしれません。式を見ただけでは、イメージが湧かないかもしれませんので、図5に、$\hat{y}_k\cdot y_k$ と $l_h^k$ の関係を示しています。ヒンジ損失の値は、$\hat{y}_k\cdot y_k$≧1のとき0で、$\hat{y}_k\cdot y_k$<1のとき $\hat{y}_k\cdot y_k$ が小さくなるほど線形に大きくなります。もう少し考えてみましょう。$\hat{y}_k$ と $y_k$ の極性が合っているとき、$\hat{y}_k\cdot y_k$ > 0 ですので、ヒンジ損失は0もしくは比較的小さい値となります。一方で、$\hat{y}_k$ と $y_k$ の極性が合っていないとき、$\hat{y}_k\cdot y_k$<0ですので、ヒンジ損失は、$\hat{y}_k$ と $y_k$ の乖離が大きいほど、大きくなります。つまり、$\hat{y}_k$ は $y_k$ の極性を当てようとするときに、有効そうな損失と言えそうです。$\hat{y}_k$ は $y_k$ の極性を当てる問題とは、2値分類です。ヒンジ損失は、2値分類を行うモデルの学習に適用される損失関数です。このことは、$\hat{y}_k$ と $y_k$ の乖離を小さくなるようにパラメータ値を決めていると言え、モデルの出力 $\hat{y}$ と所望の出力 $y$ との差違を小さくするように、パラメータ値を決める手法と解釈できます。
これまでにご紹介した目的関数と同じく、ヒンジ損失においても、各データで演算されるヒンジ損失 $l_h^k$ をすべて足したヒンジ損失和 $J_h$ が最小となるように、モデルのパラメータ値を決めます。ヒンジ損失和 $J_h$ を(5)式に示します。
$$
J_h=\sum_{k=1}^{N}l_h^k \hspace{1cm}・・・(5)
$$
このヒンジ損失和を目的関数として用いるモデルは、SVM(Support Vector Machine)です。SVMは2値分類を行うモデルであり、SVMのパラメータ値の決定問題はラグランジュの双対問題という凸2次計画問題に帰着しますが、SVMを学習時の損失関数から紐解いていくと、ヒンジ損失最小化問題と言えます。なお、SVMについては、下記の記事でより詳しく御説明しておりますので、適宜、ご参考下さい。
SVMをおさらい(ハードマージン線形SVMの編) - Qiita
SVMをおさらい(ソフトマージン線形SVMの編) - Qiita
3-4. ε-不感損失の和
ε-不感損失 $l_h^k$ は、(6)式で定義されます。
$$
l_e^k= max\{\ 0,\ |\ \hat{y}_k - y_k\ | - \epsilon\ \}\hspace{1cm}・・・(6)\\
(\epsilon > 0)
$$
ヒンジ損失と同じく、ε-不感損失は聞いたことがない、という方もいらっしゃるかもしれません。式を見ただけでは、イメージが湧かないかもしれませんので、図6に、$\hat{y}_k- y_k$ と $l_\epsilon^k$ の関係を示しています。$\hat{y}_k- y_k >\epsilon$ もしくは $\hat{y}_k- y_k < \epsilon$ のとき、$\hat{y}_k- y_k$ の値が大きくなるほどあるいは小さくなるほど、ε-不感損失の値は、線形に大きくなります。$\epsilon=0$ のとき、ε-不感損失は、絶対値誤差になりますので、ε-不感損失は、2εの不感帯を持つ絶対値誤差と言ってよいかもしれません。絶対値誤差がε以下のときは、パラメータ値を決定する際に考慮しない、というものですね。このことは、$\hat{y}_k$ と $y_k$ の乖離を小さくなるように、パラメータ値を決めていると言え、モデルの出力 $\hat{y}$ と所望の出力 $y$ との差違を小さくするように、パラメータ値を決める手法と解釈できます。
これまでにご紹介した目的関数と同じく、ε-不感損失においても、各データで演算されるε-不感損失 $l_\epsilon^k$ をすべて足したε-不感損失和 $J_\epsilon$ が最小となるように、モデルのパラメータ値を決めます。ε-不感損失和 $J_\epsilon$ を(7)式に示します。
$$
J_\epsilon=\sum_{k=1}^{N}l_e^k
\hspace{1cm}・・・(7)
$$
このε-不感損失和を目的関数として用いるモデルは、SV回帰です。前節でご紹介したヒンジ損失を2つ用意し、一つは左右反転させて、結合させたような形をしています。SV回帰はその名の通り回帰モデルですが、2値分類モデルであるSVMから派生したモデルです。目的関数からみても、派生したものであることを感じられます。SV回帰のパラメータ値の決定問題はSVMと同じくラグランジュの双対問題という凸2次計画問題に帰着しますが、SV回帰を学習時の目的関数から紐解いていくと、ε-不感損失最小化問題と言えます。
3-5. 情報利得
情報利得を(8)式に示します。ここに、$S_0$ および $S_1$ はそれぞれ事前エントロピーおよび事後エントロピーを表し、それぞれ(9)式および(10)式で定義されます。$p(a_j)$ は事象 $a_j(j=1,2,\cdots,M)$ が起きる確率を表す値です。
$$
J_g=S_0-S_1\hspace{1cm}・・・(8)\\
S_0=\sum_{j=1}^{M}(-p^0(a_j)\cdot log\ p^0(a_j)\ )\hspace{1cm}・・・(9)\\
S_1=\sum_{j=1}^{M}(-p^1(a_j)\cdot log\ p^1(a_j)\ )\hspace{1cm}・・・(10)\\
0\leq p(a_j)^i\leq 1
$$
(8)式から情報利得は、例えばなんらかの現象や処理が起きる前のエントロピーと起きた後のエントロピーの差です。では、エントロピーとは、どのような意味を持つ値なのでしょうか。(9)式もしくは(10)式を見てみますと、
$-p(a_j)\cdot log\ p(a_j)$ → $p(a_j) \cdot (-1\cdot log\ p(a_j)$ → $p(a_j)\cdot log\ 1/p(a_j)$
と変形できます。$log\ 1/p(a_j)$ は、$p(a_j)$ が0に近づくほど$\infty$に近づき、$p(a_j)$ が1に近づくほど0に近づきます。つまり、 $log\ 1/p(a_j)$ は、事象 $a_j$ の起きにくさ、あるいは、不確定さと言えそうです。$log\ 1/p(a_j)$ に、事象 $a_j$ が起きる確率 $p(a_j)$ を掛けていますので、$p(a_j)\cdot log\ 1/p(a_j)$ は、不確定さの期待値と言えそうです(100円もらえる確率が0.5のとき、その期待値は50円ですね)。
以上から、(9)式は、事象 $a_1, a_2, \cdots, a_M$ を取り得る事象に対して、なんらかの現象や処理が起きる前の不確定さであり、(10)式は、なんらかの現象や処理が起きた後の不確定さと言えそうです。とするならば、(8)式で表される情報利得は、なんらかの現象や処理が起きる前に対して起きた後では、どの程度不確定さが下がったかを表す量と言えそうです。つまり、情報利得が大きいほど、なんらかの現象や処理が起きた後では、事象 $a_1, a_2, \cdots, a_M$ のうち、どの $a_j$が起きるかが、より確定的になった、と言ってよさそうです。
この情報利得を予測性能に結びつけて考えますと、情報利得が大きいほど、処理を行う事によって、より確定的になったと言えますので、処理を行う事によって予測精度がより高まったと言えそうです。したがって、情報利得が大きくなるようにモデルのパラメータ値を決めれば、そのモデルの予測精度は高くなる、と言えます。これが、情報利得です。図7は、情報利得の考え方を簡単に示しています。なんらかの現象や処理が起きる前の事象 $a_1, a_2, a_3, a_4$ が起きる確率 $[p^0(a_1), p^0(a_2), p^0(a_3), p^0(a_4)]$ は、$[0.25, 0.25, 0.25, 0.25]$ であるのに対して、起きた後の事象 $a_1, a_2, a_3, a_4$ が起きる確率 $[p^1(a_1), p^1(a_2), p^1(a_3), p^1(a_4)]$ は、$[0, 1, 0, 0]$ となっています。なんらかの現象や処理が起きる前は、事象 $a_1, a_2, a_3, a_4$ の発生確率は全て0.25で、どれが発生するかわからない状況(不確定性が高い状況)でしたが、なんらかの現象や処理が起きた後は、事象 $a_2$ の発生確率は1で、それ以外の事象の発生確率は0で、事象 $a_2$ が確実に発生する状況(不確定性が低い状況)となっています。このとき、起きる前のエントロピー $S_0$は約0.6であり、起きた後のエントロピー $S_1$は0で、エントロピーが大幅に減っていることがわかります。情報利得は、約0.6となります。
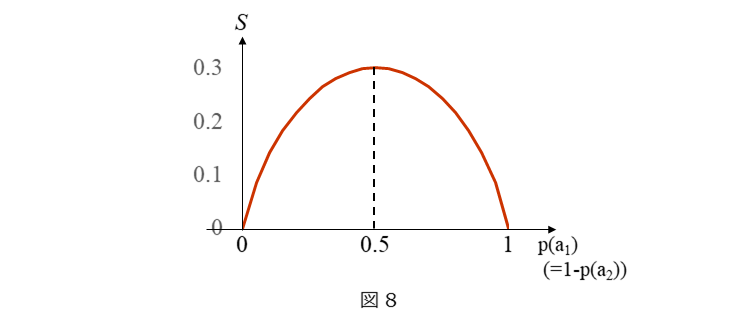
このように、エントロピーは、確実性が高いほど低くなり、確実性が低くなるほど高くなる値です(不確実性が高いほど高くなり、不確実性が低いほど低くなる値です)。図8は、$a_1$と$a_2$の2つしか起きない事象(例:コインの表/裏)の時の確率 $p(a_1)$ に対するエントロピー $S$ の関係を示しています。 $p(a_1)=0$ もしくは $p(a_2)=1$ のとき、エントロピー $S$ は0です。$p(a_1)=1-p(a_2)$ ですので、$p(a_1)=0$ のときは、$p(a_2)=1$ で、$a_1$ は確実に起きず、$a_2$ は確実に起きますので、確実性はいわば100%です。$p(a_1)=1$ のとき、$p(a_2)=0$ で、$a_1$ は確実に起きず、$a_2$ は確実に起きますので、確実性はいわば100%です。したがって、エントロピー $S$ の値はもっとも低くなります。逆に $p(a_1)=0.5$ のとき、エントロピー $S$ は約0.3です。$p(a_1)=0.5$ のとき、$p(a_2)=0.5$ ですので、$a_1$と$a_2$ のどちらが起きるかは、文字通り五分五分でどちらが起きるか分かりませんので確実性はもっとも低いと言えます。したがって、エントロピー $S$ の値はもっとも高くなります。以上から、なんらかの現象や処理の起きる前と起きた後のエトロピー差である情報利得は、当該現象や処理により、どの程度、不確定さが減ったかを表す値であると言えます。
情報利得を目的関数として用いるモデルとして、決定木があります。決定木の学習は、各ノード(分岐)でどのような属性(分岐条件)で分類するのが良いかを選ぶことと言えますが、この学習を行うときに、そのノードを通過することで、もっとも情報利得が大きくなるような属性を選びます。情報利得が大きくなるということは、上述しましたように、ノードでの処理により、学習データに対する予測精度がより高まった(不確定さがより減少した)と言えますので、そのように属性を選ぶことで、決定木で予測される結果 $\hat{y}$ と学習データにおける $y$ との 乖離を小さくなるように、パラメータ値(ノード属性)を決めていると言えます。したがって、情報利得を用いた学習も、モデルの出力 $\hat{y}$ と所望の出力 $y$ との差違を小さくするように、パラメータ値を決める手法と解釈できます。なお、情報利得として、エントロピーの差ではなく、ジニ係数と呼ばれる値の差を用いることもあります。
3-6. 交差エントロピーの和
交差エントロピー $l_e$ を(11)式に示します。$j$ は、クラス番号を表しますので、クラス分類を行うモデルの学習に用いられそうと予想がつきます。また、交差エントロピーは、前述のエントロピーと文言も式も似ています。
$$
l_e^k=ー\sum_{j=1}^{M}\ y_k^j\cdot log\ \hat{y}_k^j\hspace{1cm}・・・(11)\
j:クラス番号
$$
具体的に考えてみましょう。クラス数が4 ($M$=4) のときを考えてみます。このとき、$k$ 番目のデータは、クラス番号3が正解とします。すなわち、$[\ y_k^1, y_k^2, y_k^3, y_k^4\ ]=[\ 0, 0, 1, 0\ ]$ です。このとき、(11)式は、$l_e^k=-log\ \hat{y}_k^3$ であり、正解クラス番号のみの $-log\ \hat{y}_k$ の値を考えればよいことがわかります。$\hat{y}_k$ は、分類対象がそのクラスである可能性(確率)を表す値と考えられますので、$0\leq\hat{y}_k\leq1$ とします。このとき、$-log\ \hat{y}_k$ の値は、$\hat{y}_k$ が0に近づくほど(正解から遠ざかるほど)$\infty$に近づき、$\hat{y}_k$ が1に近づくほど(正解に近づくほど)0に近づくことがわかります。すなわち、交差エントロピーとは、複数のクラス分類を行うとき、$y^j$ が0もしくは1の値をとり、$0\leq\hat{y}_k^j\leq1$であるときの $y$ に対する $\hat{y}$ の差違を表していると言えます。エントロピーの形をしつつ、 $y$ に対する $\hat{y}$ の差違を表していることから交差エントロピーと呼ばれます。交差エントロピーを用いた学習もモデルの出力 $\hat{y}$ と所望の出力 $y$ との差違を小さくするように、パラメータ値を決める手法と解釈できます。各データで演算される交差エントロピー $l_e^k$ をすべて足した交差エントロピーの和が最小となるように、モデルのパラメータ値を決めます。交差エントロピーの和 $J_e$ を(12)式に示します。
$$
J_e=ー\sum_{k=1}^{N}\ l_e^k\hspace{1cm}・・・(12)
$$
この交差エントロピーの和を目的関数として用いるモデルとして、深層学習があります。上述しましたように、交差エントロピーの和は、多クラス分類問題を行うモデルの学習を行う際に適切な目的関数ですので、多クラス分類を行う深層学習の学習に用いられます。3-1で紹介しました二乗和誤差も深層学習の学習に用いられますが、特に深層学習による回帰を行う場合に二乗和誤差は用いられます。
ちなみに、「3-2 尤度」で触れましたロジスティック回帰は対数尤度を最大化することで、そのパラメータ値を得ると述べましたが、この対数尤度最大化は、交差エントロピー最小化と等価です。ロジスティック回帰は、2クラス分類問題とも解釈できますが、交差エントロピー最小化としてパラメータ値を求めても、対数尤度最大化としてパラメータ値を求めても理論上は同じ値が得られます。私の理解では、尤度は統計学の枠組みの値で、交差エントロピーは情報理論の枠組みの値です。両者が同じ値を示しているのは、両者とも2つの確率分布の差違を表そうとしていることに端を発しているためと考えています。
4. まとめ
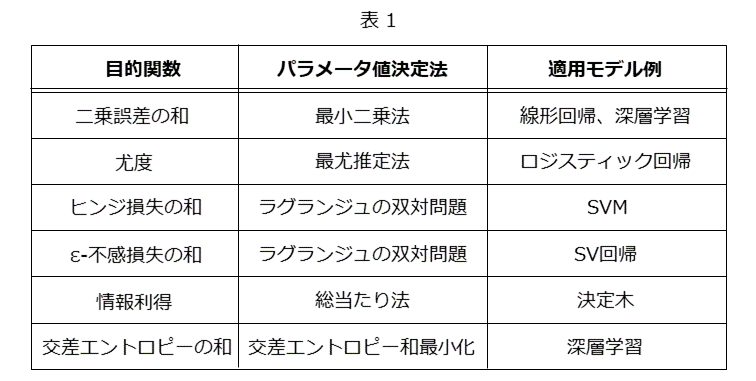
3章でご紹介しました6つの目的関数をあらためて表1にまとめました。
表1に示しました目的関数以外にも、さまざまな目的関数がありますので、ご興味がありましたら、調べてみて下さい。また、今回、ご紹介しました目的関数は、モデルの出力と所望の出力との差違を評価する関数ですが、この関数に正則項と呼ばれる過学習抑制やスパース化の効果を持つ項を加えて目的関数とすることもあります。正則項については、機会がありましたらあらためてご紹介したいと思います。
5. おわりに
今回は、さまざまな目的関数とそれに対応する機械学習を紹介することで、機械学習を目的関数から考えてみました。教師あり学習と教師なし学習の一部は、目的関数の値を最小化もしくは最大化することで、モデルのパラメータ値を決めますので、今回ご紹介しました目的関数をより一般化することで、目的関数最適化として教師あり学習と教師なし学習の一部を体系的に扱うことができるかもしれません。機械学習は、モデル構造や性能に目が行きがちかもしれませんが、目的関数は、そのモデルのいわば教育方針を示していると言っても良い重要な役割を果たしているのではないかと思っています。いつもとは違う角度からの見方で面白いな、と思った方がいらっしゃれば幸いです。
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
杉山将:イラストで学ぶ機械学習
竹内一郎、鳥山昌幸:サポートベクトルマシン
岡谷貴之:深層学習
元田 浩他:データマイニングの基礎