こんにちは、(株)日立製作所 Lumada Data Science Lab. の中川です。普段は人工知能を制御に適用する研究に従事しています。近年、機械学習が注目される中、機械学習理論および機械学習を使った技術開発環境は急速に進歩すると共に、多くの方がデータサイエンスに関わるようになってきました。すでにデータサイエンスに携わっている方や、これからデータサイエンスに関わってみようと思っている方の中で、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから基本的な内容で記事を書きます。今回は、ロジスティック回帰についてご紹介します。
1. はじめに
ロジスティック回帰は、目的変数を確率で扱う場合に適用する線形モデルです。線形回帰は目的変数は、-$\infty$から$\infty$までの値を取りえますが、ロジスティック回帰では、目的変数は0~1の値となります。本記事では、ロジスティック回帰を以下の内容であらためて、おさらいします。
・ロジスティック回帰を直感的に理解する
・ロジスティック回帰の歴史を紐解く
2. ロジスティック回帰を直感的に理解する
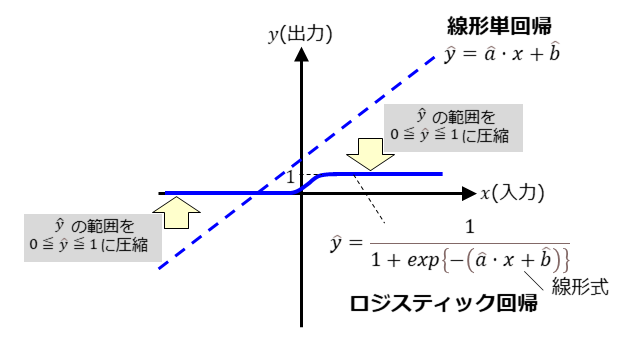
下図にロジスティック回帰の直感的な理解を示しています。ロジスティック回帰は、線形単回帰の$\hat{y}$の範囲を0$\leq\hat{y}\leq$1に圧縮するような式になっています。ロジスティック回帰は、$\hat{y}$が確率であることを想定した式であると言えます。
上図中のロジスティック回帰の式は、(1)式に示すようにパラメータが$\hat{a}$と$\hat{b}$の2つですが、(2)式のように、パラメータ数を拡張できます。
$$
\begin{align}
\hat{y}&=\frac{1}{1+exp(-(\hat{a}x+\hat{b}))}\hspace{6cm}・・・(1)\
\mspace{1cm}\
\hat{y}&=\frac{1}{1+exp(-(\hat{a}_1x_1+\hat{a}_2x_2+\cdots+\hat{a}_nx_n+\hat{b}))}\hspace{1.3cm}・・・(2)\
\mspace{1cm}\
&n:1,2,3,・・・\hspace{13.5cm}\
\end{align}
$$
(2)式におけるパラメータ $\hat{a}_1, \hat{a}_2, ・・・, \hat{a}_n, \hat{b}$ のパラメータ値を決定する場合、一般に最尤推定法が用いられます。最尤推定法については、今回は、御説明しませんが、線形回帰のパラメータ値を決定する場合は、一般に最小二乗法が用いられますので、その点も、線形回帰とロジスティック回帰は異なります。ロジスティック回帰で最尤推定法を用いるのは、上述しましたように、確率を扱うことが主な理由です。
3. ロジスティック回帰の歴史を紐解く
3-1. フラミンガム研究
前章で、ロジスティック回帰と線形単回帰とを関連付けて説明しました。本章では、ロジスティック回帰の歴史を紐解くことで、理解を進めて行きたいと思います。
ロジスティック回帰は、フラミンガム研究と呼ばれる研究で、ある疾患の発生にリスク要因がどの程度寄与しているかを調べるために開発された方法です。具体的には、アメリカのフラミンガムという町の住人を対象として心血管病の原因を調査するために1948年に開始されました。フラミンガムの住人を対象としたアンケート調査結果(リスク要因)と心血管病の発生状況の関係を調べることで、心血管病の発生原因とその寄与度を探りました。この研究において、複数のリスク要因と心血管病の発生確率を結びつける方法として、ロジスティック回帰が開発されました。
ロジスティック回帰では、次の2つの仮定をおいています。
・リスクをオッズで表せる。
・リスク要因が複数あるときのある事象(疾患)の発生確率を、個々のリスクのオッズ比の積で表せる。
以下に、詳細を説明します。
3-2. オッズ
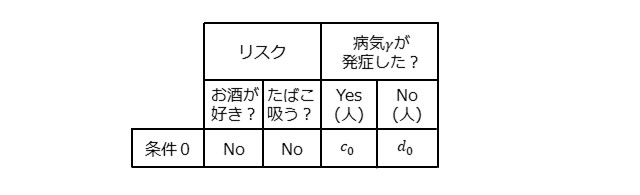
下表について考えてみます。お酒が好きではなく、たばこを吸わない人を対象として、病気$\gamma$が発症した人が$c_0$[人]、発症しなかった人が$d_0$[人]いたとします。
このとき、病気$\gamma$の発症率およびオッズは、下記となります。
$$
\begin{align}
(発症率)&=\hspace{0.2cm}\frac{c_0}{(c_0+d_0)}\
\mspace{1cm}\
(オッズ)&=\hspace{0.2cm}\frac{c_0}{d_0}\
\end{align}
$$
オッズとは、ある事象の起こりやすさを示し、以下で定義されます。
(オッズ)=(ある事象が起こる確率(回数))/(ある事象が起こらない確率(回数))
あるいは、
(オッズ)=(ある事象が起こりそうと思われる確率(回数))
/(ある事象が起こらないと思われる確率( 回数))
とも定義されます。ここでは、ある事象とは、病気$\gamma$の発症を指します。オッズは、一般的ななんらかの事象の発生率(ここでは発症率)とは異なることに注意しましょう。
3-3. オッズ比
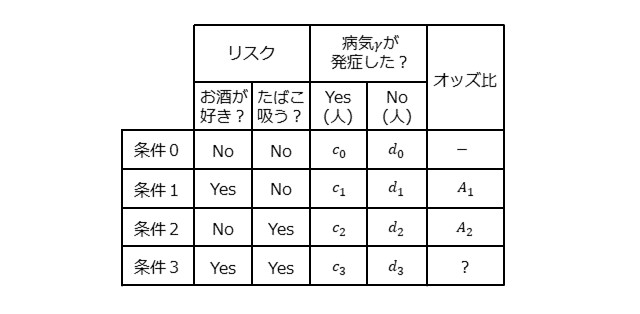
次に、下表について考えてみます。
お酒が好きでたばこを吸う人を対象として、病気$\gamma$が発症した人が$c_1$[人]、発症しなかった人が$d_1$[人]であった追加のデータが得られたとします。このとき、条件1の病気$\gamma$の発症率およびオッズは、下記となります。
$$
\begin{align}
(発症率)&=\hspace{0.2cm}\frac{c_1}{(c_1+d_1)}\
\mspace{1cm}\
(オッズ)&=\hspace{0.2cm}\frac{c_1}{d_1}\
\end{align}
$$
ここで、条件0に対する条件1のオッズ比とは、以下で定義されます。
$$
\begin{align}
(オッズ比)&=\hspace{0.2cm}\frac{(条件1のオッズ)}{(条件0のオッズ)}\
\mspace{1cm}\
&=\hspace{0.2cm}\frac{c_1/d_1}{c_0/d_0}\
\end{align}
$$
オッズ比は、2つのオッズの比であり、ある事象の起こりやすさ(ここでは病気$\gamma$の発症しやすさ)を異なる条件の間で比較した値です。
3-4. 相乗モデル
次に、下表について考えてみます。
条件1のオッズは、$c_1/d_1$ですが、オッズ比$A_1$を用いて、以下のようにも表せます。
$$
(条件1のオッズ)=\frac{c_0}{d_0}{\times}A_1
$$
同様に、条件2のオッズは、以下のように表せます。
$$
(条件2のオッズ)=\frac{c_0}{d_0}{\times}A_2
$$
ここで、条件1のオッズ比($A_1$)は、特定の前提条件ではなく、任意の条件に対する条件1のオッズ比という仮定を置きます。同じく、条件2のオッズ比($A_2$)は、特定の前提条件ではなく、任意の条件に対する条件2のオッズ比という仮定を置きます。
このとき、上表の条件3のオッズは、以下のように表せることがわかります。
$$
(条件3のオッズ)=\frac{c_0}{d_0}{\times}A_1{\times}A_2
$$
前述しましたように、$A_1$は特定の前提条件ではなく、任意の条件に対する条件1のオッズ比を表すとしましたので、前提条件が$c_0/d_0$の時においても$c_0/d_0{\times}A_2$の時においても、条件1のオッズ比は$A_1$となります。すなわち、条件1であるお酒が好きでかつたばこを吸わない場合、前提条件に依存せず病気$\gamma$のオッズは$A_1$倍になります。
同様に考えて、$A_2$は特定の前提条件ではなく、任意の条件に対する条件2のオッズ比を表すとしましたので、前提条件が$c_0/d_0$の時においても$c_0/d_0{\times}A_1$の時においても、条件2のオッズ比は$A_2$となります。すなわち、条件2であるお酒が好きではなくかつたばこを吸う場合、前提条件に依存せず病気$\gamma$のオッズは$A_2$倍になります。
以上の前提を置けば、条件0のオッズをベースオッズ($B$)としますと、条件0~3のオッズ( $p/(1-p)$ )は(3)式で表せることがわかります。
$$
\begin{align}
\frac{p}{1-p}&=B{\times}A_1^{x_1}{\times}A_2^{x_2}\hspace{3cm}・・・(3)\
&p:ある事象が起こる確率あるいはある事象が起こりそうと思われる確率\
&1-p:ある事象が起こらない確率あるいはある事象が起こらないと思われる確率\
&x_1,x_2:0か1の2値をとる\
\end{align}
$$
まとめると下表となります。
(3)式のような形を相乗モデルと呼びます。一方で、前述の仮定を置かない場合は、条件3のオッズ比($A_3$)が必要となります。このとき、条件0~3のオッズ( $p/(1-p)$ )は(4)式で表すことになります。
$$
\frac{p}{1-p}=B{\times}A_1^{x_1}{\times}A_2^{x_2}{\times}A_3^{x_3}\hspace{5.2cm}・・・\hspace{0.2cm}(4)\
$$
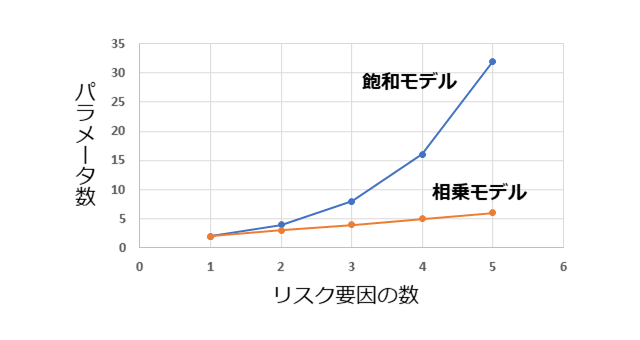
(4)式を飽和モデルと呼びます。相乗モデルではリスク要因の数だけパラメータがありますが、飽和モデルでは、リスク要因の組み合わせの数だけパラメータがあります。下のグラフは、相乗モデルおよび飽和モデルにおけるリスク要因の数に対するオッズを表すパラメータ数の関係を示しています。リスク要因の数が多くなるほど、パラメータ数の差が大きくなっていくことがわかります。パラメータ数が多くなるほど、最適化に必要なデータ量が多くなるだけでなく、パラメータ値の最適化時、モデル利用時の計算コストにも大きくなりますので、重要な性質と言って良いと思います。
3-5. リスク相乗モデルからロジスティック回帰へ
(3)式において、リスク要因の数をnとしますと、(5)式が得られます。
$$
\begin{align}
\frac{p}{1-p}&=B{\times}A_1^{x_1}{\times}A_2^{x_2}{\times}\cdots{\times}A_n^{x_n}\hspace{3.9cm}・・・\hspace{0.2cm}(5)\
&x_1,x_2,\cdots,x_n:0か1の2値をとる\
\end{align}
$$
ここで、
$$
\begin{align}
B&=e^{b}\
A_1&=e^{a_1}\
A_2&=e^{a_2}\
&\hspace{0.27cm}\vdots\
A_n&=e^{a_n}\
\end{align}
$$
とおいて、下記変形を行います。
$$
\begin{align}
\frac{p}{1-p}&=e^{b}×e^{a_1x_1}×e^{a_2x_2}{\times}\cdots{\times}e^{a_nx_n}\
&=e^{(b+a_1x_1+a_2x_2+\cdots+a_nx_n)}\hspace{4.6cm}・・・\hspace{0.2cm}(6)\
\end{align}
$$
(6)式を$p$について、解きますと、(7)式のロジスティック回帰の式が得られます
$$
p=\frac{1}{1+e^{-(b+a_1x_1+a_2x_2+\cdots+a_nx_n)}}\hspace{3.15cm}・・・\hspace{0.2cm}(7)\
$$
このように、もともとロジスティック回帰は、ある疾患の発生確率$p$を求めるための式から得られました。(7)式においては、$x_1$, $x_2$, ・・・, $x_n$は、0か1の2値しか取らないことが前提になっています。また、ベースオッズ$B$およびオッズ比$A_1$,$A_2$, ・・・, $A_n$は、0以上の値が前提となっています。
3-6. 補足
3-6-1. リスク要因が0, 1以外の離散値の場合
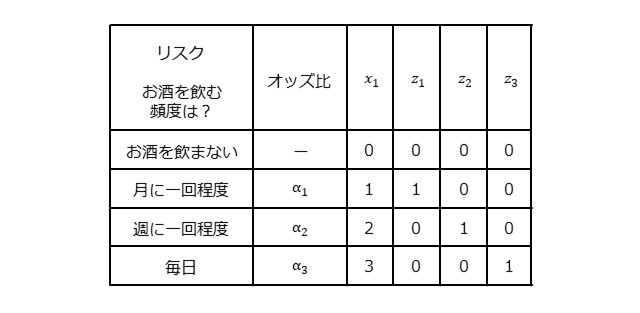
前章で紹介しましたように、ロジスティック回帰は、ある疾患の発生リスク要因の有無からある疾患の発生確率$p$を求めるための式でした。したがいまして、(7)式においては、$x_1$, $x_2$, ・・・, $x_n$は、0か1の2値しか取らないことが前提となっています。すなわち、各リスク要因があるかないかの2つを考えることが前提になっています。ここでは、$x_k$が0もしくは1以外の値を取る場合を考えます。下表は、$x_1$が、0,1,2,3の4通りの値を取る場合を考えます。下表にありますように、お酒が好きか好きでないかの2値の情報ではなく、お酒を飲む頻度を、飲まない、月に一回程度、週に一回程度、毎日の4つのカテゴリーに分けて、$x_1$の値をそれぞれ0,1,2,3としています。
お酒をのまないときのオッズをベースオッズ($B$)としたとき、オッズ( $p/(1-p)$ )は(8)式で表せます。
$$
\frac{p}{1-p}=B{\times}\alpha_1^{z_1}{\times}\alpha_2^{z_2}{\times}\alpha_3^{z_3}\hspace{5.5cm}・・・\hspace{0.2cm}(8)\
$$
$x_1$を用いる代わりに、0か1の2値しか取らない変数$z_1$,$z_2$,$z_3$を導入して、ロジスティック回帰式で扱えるようにします。このとき、$z_1$,$z_2$,$z_3$は、高々ひとつだけが1の値を取ることに注意しましょう。
3-6-2. リスク要因が連続値の場合
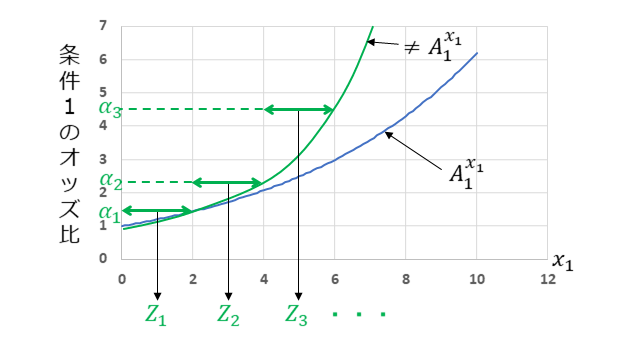
まず、$x_k$の値に対して、オッズ比$A_k$が$x_k$の累乗の関係にあるとき、 (5)式あるいは(7)式で表せます。下図は、k=1のときを例に示しており、青線がオッズ比$A_k$が$x_k$の累乗の関係にあるときです。一方で、$x_1$の値に対して、オッズ比$A_1$が累乗の関係にないときは、 $A_1$が$x_1$の累乗の関係となるように、 $x_1$を変換するなど工夫が必要となります。下図の緑線は一例を示してしています。
1つとして、3-6-1で述べました方法が適用できるように、$x_k$を区間毎に分けて、(8)式の形にすることです。上図では、($z_1$,$\alpha_1$), ($z_2$,$\alpha_2$), ($z_3$,$\alpha_3$)の決め方の一例を示しています。
あるいは、オッズ比$A_k$が$x_k$の累乗の関係となるように、もともとのリスク要因の変数値を変換するなど工夫する必要があります。
以上、ロジスティック回帰の歴史を紐解くことで、ロジスティック回帰を御説明しました。
4. おわりに
今回は、ロジスティック回帰をおさらいしました。ロジスティック回帰は、もともとは、ある疾患の発生確率を求めるために創出されたことを示し、その数理的な意味をご紹介しました。冒頭で述べたように、ロジスティック回帰は、線形回帰と考え方が近いところもあり、線形回帰における信頼区間の区間推定および検定に相当するものが、ロジスティック回帰にもあります。ロジスティック回帰における信頼区間の区間推定・検定、線形回帰との差違については、あらためて、ご紹介したいと思います。
今回も、理論の大切さをあらためて知りたいあるいは感じたいという方がいらっしゃいましたら、それをできるだけわかりやすく伝えられたら、という思いから記事を書かせて頂きました。より詳しく知りたいという方は、参考文献などをご参考頂ければと思います。
参考文献
丹後俊郎、山岡和枝、高木晴良:新版ロジスティック回帰分析 SASを利用した統計解析の実際
鶴田陽和:すべての医療系学生・研究者に贈る 独習統計学応用編24講 分割表・回帰分析・ロジスティック回帰