Go to Qiita Advent Calendar 2024 Top
LoginSignup
3
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@rudorufu1981

【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part3/22】

Last updated at Posted at 2020-05-01

目指せ水色コーダー！！！！！！

ということで、
レッドコーダーが教える、競プロ・AtCoder上達のガイドライン【中級編：目指せ水色コーダー！】(@e869120さん)

AtCoder で水色コーダー、つまりレーティング 1200 を少ない問題数で達成するために、茶色コーダー・緑コーダーにとって適切な教育的良問を 100 問集めました。

こちらの記事の初中級者が解くべき過去問精選 100 問
をPythonで解いていきます！
@e869120さんに感謝！！！！！！

###過去記事リンク
全探索：全列挙
【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part1/22】
全探索：工夫して通り数を減らす全列挙
【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part2/22】
全探索：ビット全探索
[【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part3/22】]
(https://qiita.com/rudorufu1981/items/74d5f37c26c62fc7a27f)
全探索：順列全探索
【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part4/22】
二分探索
【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part5/22】
深さ優先探索
【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part6/22】
幅優先探索
【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part7/22】

(2020/05/07 追記)
※補足
この100問解いてみたシリーズの(Part6)の記事から、入力を
input()→sys.stdin.readline().rstrip()
に変えています！
【Python】競プロテンプレ【AtCoder】
テンプレ用の記事も作ったので、よかったら使ってください〜

#「Part3」〜ビット全探索編〜
以下の5問を解いていきます！

#####全探索：ビット全探索
10　ALDS_5_A - 総当たり　基本問題です。
11　AtCoder Beginner Contest 128 C - Switches
12　AtCoder Beginner Contest 002 D - 派閥
13　JOI 2008 予選 5 - おせんべい　茶色コーダーにはやや難問ですが解くことをおすすめします。
14　Square869120Contest #4 B - Buildings are Colorful!　工夫も必要で、一筋縄では解けない難問ですが、解けば確実に力がつきます。

#10　ALDS_5_A - 総当たり
ビット全探索の最強テンプレを独自開発しました！
bit = [i>>j&1 for j in range(N)]
このテンプレを使えば、
どんなビット全探索がきても
もうなにも怖くない

test.py
def I(): return int(input())
def LI(): return list(map(int,input().split()))
n = I()
A = LI()
q = I()
m = LI()
ans = 0
partial_sum = set()
for i in range(2**n):
    bit = [i>>j&1 for j in range(n)] #最強テンプレ
    partial_sum.add(sum([A[k]*bit[k] for k in range(n)]))
for x in m:
    print('yes' if x in partial_sum else 'no')

(2020/05/04 追記)
＜別解＞
DFSでも解けます！
次の桁を足すか、足さないか、を最後まで全探索する感じです！
インデックスと和をセット、でスタックに貯めるのがポイント！！！

◆再帰Ver

test.py
def I(): return int(input())
def LI(): return list(map(int,input().split()))
n = I()
A = LI()
q = I()
m = LI()
partial_sum = set()
def dfs(i,_sum):
    if i==n:
        partial_sum.add(_sum)
        return
    dfs(i+1,_sum)
    dfs(i+1,_sum+A[i])
dfs(0,0)
for x in m:
    print('yes' if x in partial_sum else 'no')

◆スタックVer

test.py
def I(): return int(input())
def LI(): return list(map(int,input().split()))
n = I()
A = LI()
q = I()
m = LI()
partial_sum = set()
stack = [] #indexとsumを入れておく
def dfs():
    stack.append([0,0])
    stack.append([0,A[0]])
    partial_sum.add(A[0])
    while stack:
        i,s = stack.pop()
        i += 1
        if i==n:
            partial_sum.add(s)
            continue
        stack.append([i,s])
        stack.append([i,s+A[i]])
dfs()
for x in m:
    print('yes' if x in partial_sum else 'no')

※ちなみに実行時間もDFSの方が早いです〜
n,q=(20,200)のテストケース
上のコードでの計測結果！

  • ビット全探索：6.81秒
  • DFS(再帰Ver)：0.54秒
  • DFS(スタックVer)：1.03秒

#11　AtCoder Beginner Contest 128 C - Switches
Difficulty:807
ビット全探索の最強テンプレが大活躍！
問題文は少し複雑だけど、入出力例も見ながら頑張って理解して、
スイッチは最大10個なので(計算量的に)ビット全探索でいけそう！
と方針さえ立てられたらこの問題も解ける！！！
もうなにも怖くない

test.py
def LI(): return list(map(int,input().split()))
N,M = LI()
ks = [LI() for _ in range(M)]
p = LI()
ans = 0
for i in range(2**N):
    bit = [i>>j&1 for j in range(N)]
    for k,x in enumerate(ks):
        _,*s = x
        if p[k] != sum([bit[y-1] for y in s])%2:
            break
    else:
        ans += 1
print(ans)

#12　AtCoder Beginner Contest 002 D - 派閥
Difficulty:1405！！！ついに水色レベルの問題！！！
初見で解けませんでした！
ビット全探索の他に、グラフの知識があると解きやすいかも。
グラフの考えはDFSやBFSにも関わってくるので、マスターしておきたい！！！
※けんちょんさんの記事
DFS (深さ優先探索) 超入門！ 〜 グラフ・アルゴリズムの世界への入口 〜【前編】

以下のように考える！
1.人間関係を無向グラフで表す。
2.ビット全探索で、それぞれの国会議員が派閥に入っているか？入っていないかの全通り考える。
3.2のそれぞれについて、全員互いに人間関係があれば答えの候補！

test.py
import itertools
def LI(): return list(map(int,input().split()))
N,M = LI()
xy = [LI() for _ in range(M)]
ans = 1
graph = {i:[] for i in range(1,N+1)} #1_indexed
for a in xy:
    x,y = a
    graph[x].append(y)
    graph[y].append(x)
for i in range(2**N):
    bit = [i>>j&1 for j in range(N)]
    giinsuu = sum(bit)
    if giinsuu<=1:
        continue
    giinNO_bit1 = [k+1 for k in range(N) if bit[k]==1]
    for b,c in itertools.product(giinNO_bit1,repeat=2):
        if b==c:
            continue
        if not b in graph[c]:
            break
        if not c in graph[b]:
            break
    else:
        ans = max(ans,giinsuu)
print(ans)

コードの細かい補足をすると、

for b,c in itertools.product(giinNO_bit1,repeat=2):
    if b==c:
        continue
    if not b in graph[c]:
        break
    if not c in graph[b]:
        break
else:
    ans = max(ans,giinsuu)

itertools.productとfor/elseの使い方については、前回の記事
【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part2/22】
で簡単に解説しているので、こちらもあわせてご参考に・・・

また、if文のところのイメージは、過去記事
【Python】ABC133B(右上三角形問題)【AtCoder】
この記事に出てくる表の右上三角形と左下三角形をすべて計算していくイメージ！！！
この表のイメージが持てたら、コードもすらすらかけると思う！

#13　JOI 2008 予選 5 - おせんべい
初見で解けませんでした！！
NumpyとXOR(排他的論理和 ^)の知識があると解きやすいかも。

  • Numpy
    　2次元配列以上のデータを扱う時に、コードが複雑にならないのでロジックがわかりやすくなる
  • XOR(演算子：^)
    「0 or 1」で表せるものは「0⇄1」という操作をするときに相性良さそう(0^1→1、1^1→0)

と、すごい人たちのACコードを見て思いました。

以下のように考える！
1.すべての行のひっくり返す/ひっくり返さないの全パターンを調べる
2.1のそれぞれのパターンに対し各列の1の数をカウント(=black)
3.2で出荷できるのは、0の数=>つまりR-black。
ただし、列もひっくり返せるので
R-blackとblackの大きいほう！の各列の結果をすべて足したものが答えの候補！

各列の1の数のカウントは、各列を足し算すれば答えが出る。
（各列の足し算とかはNumpyの十八番！）

test.py
import numpy as np
def LI(): return list(map(int,input().split()))
R,C = LI()
a = np.array([LI() for _ in range(R)])
ans = 0
for i in range(2**R):
    bit = np.array([[i>>j&1 for j in range(R)]]).T
    black = (a^bit).sum(axis=0)
    ans = max(ans,np.fmax(R-black,black).sum())
print(ans)

案外短いコードだった！

コードの細かい補足をすると、

bit = np.array([[i>>j&1 for j in range(R)]]).T

Tは転置してくるものであるが、
[こちらのサイト]
(https://deepage.net/features/numpy-transpose.html)
より、転置の対象が2次元以上でないと効果を発揮してくれない！
転置の対象が1次元
np.array([i>>j&1 for j in range(R)]).T
ではだめ。

以下のいずれかの書き方でかける。どれでもいい！

  • np.array([[i>>j&1 for j in range(R)]]).T
  • np.matrix([i>>j&1 for j in range(R)]).T
  • np.array([i>>j&1 for j in range(R)]).reshape(R,-1)
  • np.array([[i>>j&1] for j in range(R)])
black = (a^bit).sum(axis=0)

a^bitは、こんな感じ〜
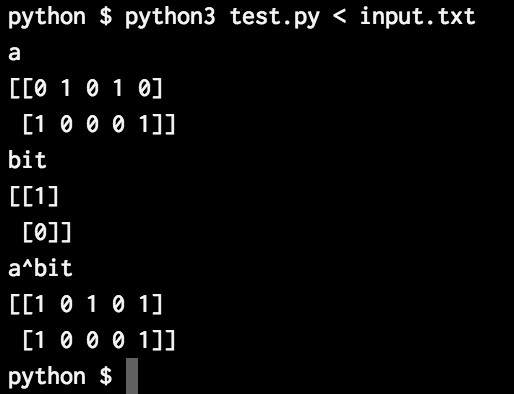
スクリーンショット 2020-05-01 14.10.15.png
1とのXOR(演算子：^)を使えば、ひっくり返る！！！！！
上の例だと、上の行だけひっくり返っている！下の行はそのまま！
すごい！！！！！！

各列の1の数のカウントは、各列を足し算すればいい。
各列の足し算は、axis=0で足し算できる！
axisについては、
こちらの記事
がわかりやすかった！

ans = max(ans,np.fmax(R-black,black).sum())

R-blackは、こんな感じ〜
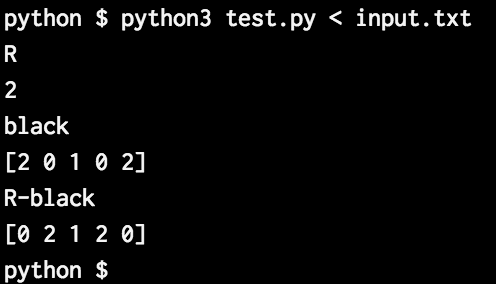
スクリーンショット 2020-05-01 14.41.21.png
イメージ的には、以下の2つは一緒！

  • 2 - [2 0 1 0 2] = [0 2 1 2 0]
  • [2 2 2 2 2] - [2 0 1 0 2] = [0 2 1 2 0]

np.fmaxについては、
[こちらのサイト]
(https://note.nkmk.me/python-numpy-maximum-mimimun-fmax-fmin/)
がわかりやすかった！

結論！
NumpyとXORはすごい！！！！！！

#14　Square869120Contest #4 B - Buildings are Colorful!
初見で解けそうだったけど、解けなかった！！！
くやしい！
bitが0のときも、建物のkijunの高さが増えていくパターンに気付けなかった・・・

でもこれまでのビット全探索の問題がすべて理解できれば、考え方自体はそこまで難しい問題ではない！

test.py
def LI(): return list(map(int,input().split()))
N,K = LI()
a = LI()
ans = float('INF')
for i in range(2**(N-1)):
    bit = [i>>j&1 for j in range(N-1)]
    if K-1!=sum(bit):
        continue
    cost,kijun = 0,a[0]
    for k in range(N-1):
        if bit[k]==0:
            kijun = max(kijun,a[k+1])
            continue
        if a[k+1]>=kijun+1:
            kijun = a[k+1]
            continue
        cost += (kijun+1)-a[k+1]
        kijun += 1
    ans = min(ans,cost)
print(ans)

次回は、以下の3問を解いていきます！

#####全探索：順列全探索
15　AtCoder Beginner Contest 145 C - Average Length
16　AtCoder Beginner Contest 150 C - Count Order
17　ALDS_13_A - 8 クイーン問題　面白いです。

Part3/22
おわり！

次(Part4/22)へ

3
7
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
7

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?