【Python】ABC133B(右上三角形問題)【AtCoder】

プログラム初心者がつまずきそうな箇所。
重複なしの2重ループ。
俺はこれ系の問題を右上三角形問題と勝手に定義しているw

ABC133B

Difficulty:137
添字とかあると問題理解するのが大変・・・
とりあえずD次元とかいわれても想像できないので2次元でイメージする。
要は
①異なる2点間の距離の組み合わせすべて計算して
②それぞれの距離が整数かどうか
を調べればおk

①異なる2点間の距離の組み合わせすべて計算

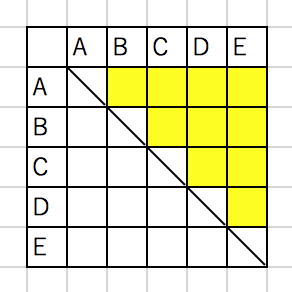異なる2点間の距離の組み合わせ
=右上の三角形（黄色の部分！）を全探索すればよい！だから右上三角形問題！！！
（A点とB点、A点とC点、・・・D点とE点）

右上三角形の全探索(5行*5列)をコードにするとこんな感じ

test.py

for i in range(5):
    for j in range(i+1,5):
        #距離の計算

iは、0行目(A行)、1行目(B行)、2行目(C行)、3行目(D行)、4行目(E行)
iが0のときjは、range(1,5)→1,2,3,4
iが1のときjは、range(2,5)→2,3,4
iが2のときjは、range(3,5)→3,4
iが3のときjは、range(4,5)→4
iが4のときjは、range(5,5)→なしなのでなにも処理されません。
⇨しっかり右上の三角形（黄色の部分！）の10箇所(4+3+2+1+0)が全探索できてる！

ここが理解できれば、どんな右上三角形問題が来ても「もう何も怖くない」

②それぞれの距離が整数かどうか

こっちは簡単。
%1==0 or is_integer
どっちでもいいと思うよ。俺は英語苦手マンなので前者を使います。

①＋②

まとめるとこんな感じかなぁ

test.py

def LI(): return list(map(int,input().split()))
N,D = LI()
X = [LI() for _ in range(N)]
_ans = 0
for i in range(N):
    for j in range(i+1,N):
        temp = 0
        for k in range(D):
            temp += (X[j][k]-X[i][k])**2
        if temp**0.5%1==0:
            _ans += 1
print(_ans)

temp = 0の記述する場所は、問題数をこなしていけば感覚的にわかるようになると思う。
あと2点間の距離の公式は中学数学を思い出す事！

類題 (右上三角形問題の重複なしの３重ループ問題)

これとくとより理解が深まると思います。
AOJ(ITP1_7_B) 組み合わせの数

こんな感じ〜

test.py

def LI(): return list(map(int,input().split()))
while 1:
    n,x = LI()
    if n==x==0:
        break
    _ans = 0
    for i in range(1,n+1):
        for j in range(i+1,n+1):
            for k in range(j+1,n+1):
                if i+j+k==x:
                    _ans += 1
    print(_ans)

この記事の本題とは外れますが、おまけのおまけの話をすると、
k=x-i-j (kの条件：1<=k<=n and j<k)
とおくことで2重for文で解けます！！！

(2020/05/07 追記)
現在は、上の3重for文の問題
itertools.combinationsを使ってコードを書きます！
詳細はこちら！
【Python】初中級者が解くべき過去問精選 100 問を解いてみた【Part1/22】

(2020/05/26 追記)

※補足
上の図において

• 右上三角形の全探索
  • itertools.combinations(range(N),2)
• 右上三角形+斜線部分の全探索
  • itertools.combinations_with_replacement(range(N),2)

となります。
itertools.combinations_with_replacementは重複組み合わせ！！！

おわり！