はじめに
今回は機械学習のアルゴリズムの一つであるサポートベクトルマシンについての理論をまとめていきます。
お付き合い頂ければ幸いです。
サポートベクトルマシンの理論
それでは最初にサポートベクトルマシンの理論についてまとめていきます。
ハードマージンとソフトマージン
サポートベクトルマシン(svm)は汎化性能や応用分野の広さから、データ分析の現場でよく用いられる機械学習のアルゴリズムの一つです。
マージン最大化と呼ばれる考えに基づき、主に2値分類問題に用いられます。多クラス分類や回帰問題への応用も可能です。
計算コストが他の機械学習のアルゴリズムと比較して大きいため、大規模なデータセットには向かないという弱点があります。
線形分離可能(一つの直線で二つに分けられる)なデータを前提としたマージンをハードマージン、線形分離不可能なデータを前提として、誤判別を許容するマージンをソフトマージンと呼びます。
線形分離可能を一つの直線で二つに分けられると書きましたが、これは2次元のデータにおいてのみであるので、線形分離可能の概念を一般化してn次元空間上の集合をn-1次元の超平面で分離できることを線形分離可能と定義します。
二次元の平面上のデータを一次元の線で分類できるとき、それは線形分離可能であるといえます。また、三次元の空間上のデータを二次元の平面で分類できるときも、線形分離可能であるといえます。
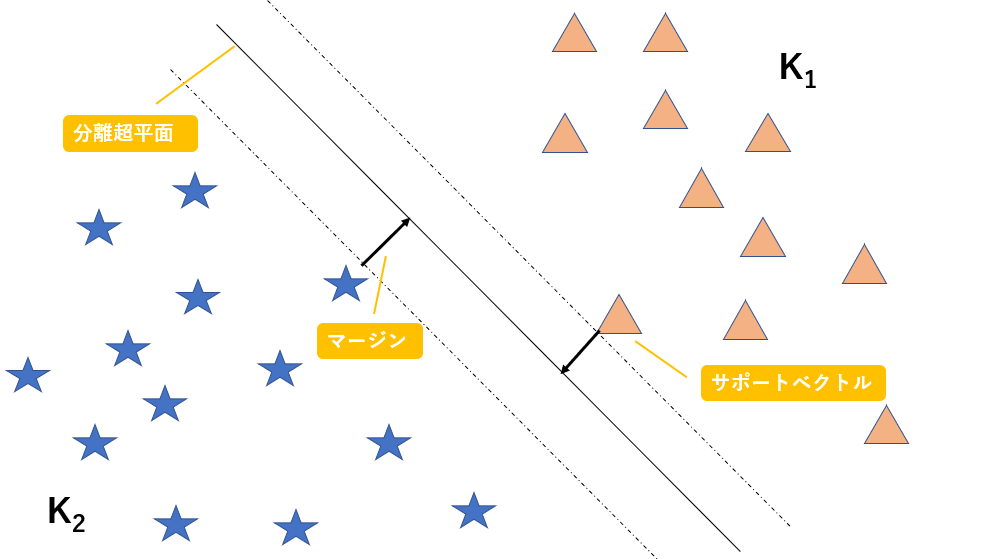
このように、n次元のデータを分類するn-1次元の平面(厳密には平面ではない)を分離超平面と呼び、また分離超平面とその分離超平面に最も近いデータとの距離をマージンと呼び、このマージンを最大化することがこのアルゴリズムの目標になります。
また、分離超平面に最も近いでデータのことをサポートベクトルと呼びます。以下に図解します。
図に示すマージンを最大化するような超平面を作成することで精度を上昇させることができるのは、直感的に明らかですよね。
図示するために今回は二次元でデータを表現しましたが、n次元空間上のデータをn-1次元の超平面で分割していると考えてください。
二次元の数ベクトル空間上においては、上の図のように二つのデータを分割する直線を$ax + by + c = 0$と表すことができ、パラメータ$a, b, c$を調整することで全ての直線を表すことができます。
n次元数ベクトル空間の超平面の式
今回はn次元数ベクトル空間上の超平面を想定しているので、その超平面の式を以下数式で与えられます。今、全部でN個のデータが存在する場合を考えます。
$$W^TX_i + b = 0 \quad (i = 1, 2, 3, ...N)$$
それではこの超平面の式を用いて、ハードマージン(線形分離可能な問題)の最適化に用いる式を導出しましょう。
ハードマージン最適化の式を導出
$W^TX_i+b=0$の部分を計算すると、$w_1x_1 + w_2x_2 + ...w_nx_n+b=0$となり、これは二次元における直線の式である$ax + by + c = 0$をn次元に拡張した超平面の式であることが感覚的に理解できると思います。
図の三角のデータは$K_1$の集合に属していて、図の星のデータは$K_2$の集合に属していると考えると、以下の式を満たすことが分かります。
W^TX_i + b > 0 \quad (X_i \in K_1)\\
W^TX_i + b < 0 \quad (X_i \in K_2)
この式をまとめて表すためにラベル変数tを導入します。
i番目のデータ$x_i$がクラス1に属するときに$t_i=1$、クラス2に属するときに$t_i=-1$とします。
t_i = \left\{
\begin{array}{ll}
1 & (X_i \in K_1) \\
-1 & (X_i \in K_2)
\end{array}
\right.
このように定義した$t_i$を用いると、条件式を以下のように表すことができます。
$$t_i(W^TX_i + b) > 0 \quad (i = 1, 2, 3, ...N)$$
このように、条件式を一行で表すことができました。
マージンはn次元空間上の点と超平面との距離になるので、点と直線の距離について復習しましょう。二次元の点と直線の距離は、点を$A(x_0,y_0)$ 、直線を$l:ax+by+c=0$とすると以下の式で表されましたね。
d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2+b^2}}
n次元空間上の1点と超平面との距離は以下の式で表されます。
d = \frac{|w_1x_1 + w_2x_2... + w_nx_n + b|}{\sqrt{w_1^2+w_2^2...+w_n^2}} = \frac{|W^TX_i + b|}{||w||}
よって、ここまでの式からマージンMを最大化するという条件は以下の式で表されます。
max_{w, b}M, \quad \frac{t_i(W^TX_i + b)}{||W||} \geq M \quad (i = 1, 2, 3, ...N)
ちょっとよく分からないと思うので、解説します。
あるデータ$X_a$を選んだときの、$X_a$と超平面$W^TX + b=0$との距離は、$ \frac{t_i(W^TX_a + b)}{||W||}$と表されますね。
$|W^TX_a + b|$をラベル変数tを用いて$t_i(W^TX_a + b)$と表しています。
また、$max_{w, b}M$は変数$w, b$のもとでMを最大化するという意味であり、$\frac{t_i(W^TX_i + b)}{||W||} \geq M $という条件は、超平面と全てのデータとの距離をマージンMよりも大きくするということを表しています。
よって、この数式を満たすMを求めるということが、サポートベクトルマシンを最適化するということになります。
ここで、$\frac{t_i(W^TX_i + b)}{||W||} \geq M $の両辺をMで割り、以下の条件を導入します。
\frac{W}{M||W||} = \tilde{W}\\
\frac{b}{M||W||} = \tilde{b}
すると、最適化問題の条件式は以下のように表されます。
t_i(\tilde{W^T}X_i + \tilde{b}) \geq 1
全てのデータに対して上の式は成り立ちますが、等号が成り立つときの$X_i$が最も近いデータの$X_i$になります。
つまり、マージンMを簡略化した $\tilde{M}$は以下の式で表されます。
\tilde{M} = \frac{t_i(\tilde{W^T}X_i + \tilde{b})}{||\tilde{W}||} = \frac{1}{||\tilde{W}||}
この式変形により、最適化問題は以下のようになります。
max_{\tilde{W}, \tilde{b}}\frac{1}{||\tilde{W}||}, \quad t_i(\tilde{W^T}X_i + \tilde{b}) \geq 1 \quad (i = 1, 2, 3, ...N)
結構難しくなってきましたね。頑張っていきましょう。
途中の式変形でチルダがついてしまいましたが、簡単のために取っ払いましょう。そして、$\frac{1}{||\tilde{W}||}$の部分については、ノルムの逆数を最大化するという意味ですので、簡単のためにノルムを二乗を最小化する問題に変換しましょう。ここの部分の式変形は少しごり押しです。後の計算を簡単にするために$\frac{1}{2}$をつけます。
min_{W, b}\frac{1}{2}||W||^2, \quad t_i(W^TX_i + b)\geq 1 \quad (i = 1, 2, 3, ...N)
上記の式を解くこと、つまり$t_i(W^TX_i + b)\geq 1$という条件の下で$\frac{1}{2}||W||^2$を最小化することによりマージンを最大化することができます。これが線形分離可能な場合の最適化問題の式になります。
しかし、この条件では線形分離可能な問題しか解くことができません。つまり、ハードマージンにしか適用できません。
この式をソフトマージンにも適用できるように、制約条件を緩めましょう。
ソフトマージンの最適化の式を導出
上記の式の制約条件$t_i(W^TX_i + b)\geq 1$を緩めることで、線形分離不可能な問題(ソフトマージン)にも対応できるようにしましょう。
以下に図解します。
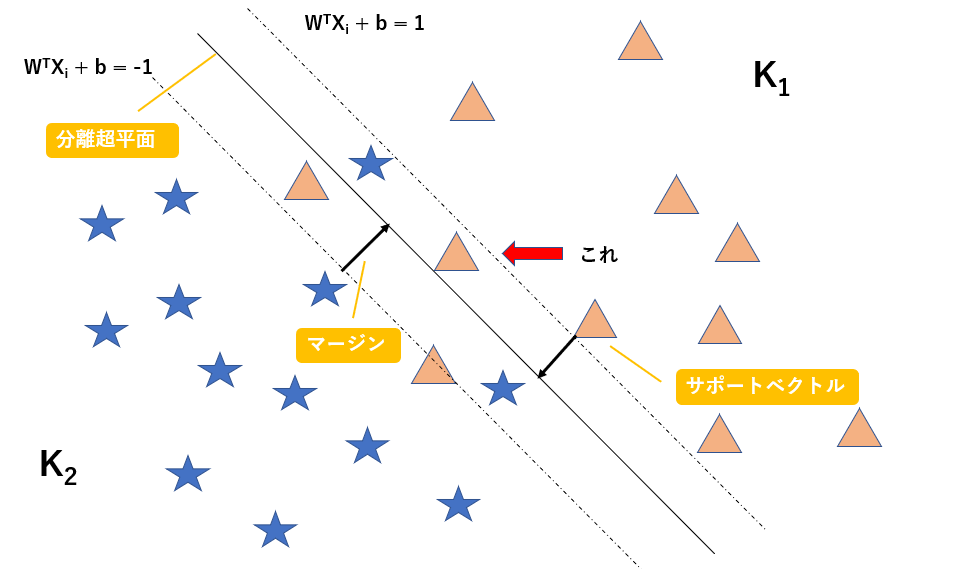
この図のように線形分離不可能な問題を考えます。図の赤矢印で示すように、マージンの内側にデータが入り込んでしまっています。
$W^TX_i + b = 1$を満たす超平面上にサポートベクトル(超平面に最も近いデータ)が存在するのはここまでの話から考えると当然ですね。
図の赤矢印で示すデータは$ t_i(W^TX_i + b)\geq 1$を満たしていませんが、$ t_i(W^TX_i + b)\geq 0.5$という条件なら満たすかもしれません。
よって、スラッグ変数$\xi$を導入することで制約条件を緩めることにしましょう。以下のように定義します。
t_i(W^TX_i + b)\geq 1 - \xi_i \\
\xi_i = max\Bigl\{0, M - \frac{t_i(W^TX_i + b)}{||W||}\Bigr\}
以上の式より、データがマージンの内側にある場合にのみ、制約を緩めることにします。
よって、このスラッグ変数を導入することにより、マージン最適化問題は以下のようになります。
min_{W, \xi}\Bigl\{\frac{1}{2}||W||^2 + C\sum_{i=1}^{N} \xi_i\Bigr\} \quad 制約条件\quad
t_i(W^TX_i + b)\geq 1 - \xi_i\\
\xi_i = max\Bigl\{0, M - \frac{t_i(W^TX_i + b)}{||W||}\Bigr\}\\
i = 1, 2, 3, ... N
マージンを最大化しようとする、つまり$\frac{1}{2}||W||^2$を最小化すると当然マージンの中に入ってくるデータが増えるため、$C\sum_{i=1}^{N} \xi_i$が増加します。よって、この最適化問題は相反する二つの項のバランスを取りながら最小化をはかることになります。
Cハイパーパラメーターであり、私たちが調節しながらモデルを構築することになります。
ここまでの復習
ここまでで、ハードマージンとソフトマージンにおける最適化問題の式を導出しました。以下にまとめます。
ハードマージンのとき
min_{W, b}\frac{1}{2}||W||^2, \quad t_i(W^TX_i + b)\geq 1 \quad (i = 1, 2, 3, ...N)
ソフトマージンのとき
min_{W, \xi}\Bigl\{\frac{1}{2}||W||^2 + C\sum_{i=1}^{N} \xi_i\Bigr\} \quad \quad
t_i(W^TX_i + b)\geq 1 - \xi_i\\
\xi_i = max\Bigl\{0, M - \frac{t_i(W^TX_i + b)}{||W||}\Bigr\}\\
i = 1, 2, 3, ... N
ソフトマージンは線形分離不可能な問題のときに用いるもので、ハードマージンは線形分離可能な問題のときに用いるものでしたね。
最適化問題を解く
それでは最適化問題を解いていくことを考えていきましょう。
この最適化問題を解くときに、上記の式を直接解くことはほとんどありません。
上記のような式を最適化問題の主問題といいますが、多くの場合この主問題を直接解くのではなく、この主問題を双対問題と呼ばれる別の形の数式に変換して、その数式を解くことで最適化問題を解いていきます。
今回、この最適化問題を解くためにラグランジュの未定乗数法を用いましょう。
ラグランジュの未定乗数法についてはこちらの記事を参考にしてください。
自分も完全に理解している訳ではないので、一部厳密性に欠ける部分があると思いますがご了承ください。簡単に解説します。
ラグランジュの未定乗数法について
ラグランジュの未定乗数法は制約付き最適化問題の代表的な手法です。
目的関数$f(X)$をn個の不等式制約$g(X)_i \leqq0, i = 1, 2, 3, ...n$の条件の下で最小にするときを考えます。
まず、以下のラグランジュ関数を定義します。
L(X, α) = f(X) + \sum_{i=1}^{n}α_ig_i(X)
この不等式制約付き最適化問題は、ラグランジュ関数について以下の四つの条件を満たす$(\tilde{X}, \tilde{α})$を求める問題に帰結します。
\frac{\partial L(X, α)}{\partial X}=0\\
\frac{\partial L(X, α)}{\partial α_i} = g_i(X)\leqq 0, \quad (i=1, 2,... n)\\
0 \leqq α, \quad (i = 1,2, ...n)\\
α_ig_i(X) = 0, \quad (i = 1, 2,...n)
このように、最適化問題を直接解くのではなく、ラグランジュの未定乗数法を用いることで別の式を用いて最適化問題を解くことができます。この別の式を双対問題と呼ぶのでしたね。
最適化問題に適用
それでは、サポートベクトルマシンのソフトマージンの式にラグランジュの未定乗数法を適用してみましょう。
目的関数は以下です。
min_{W, \xi}\Bigl\{\frac{1}{2}||W||^2 + C\sum_{i=1}^{N} \xi_i\Bigr\}
不等式制約は以下です。
t_i(W^TX_i + b)\geq 1 - \xi_i \quad \xi_i \geq 0 \quad i = 1, 2,...N
今回はn個のデータ全てに不等式制約が二個ずつあるため、ラグランジュ乗数をα、βとすると、ラグランジュ関数は以下のようになります。
L(W,b,\xi,α,β)=\frac{1}{2}||W||^2 + C\sum_{i=1}^{N} \xi_i-\sum_{i=1}^{N}α_i\bigl\{t_i(W^TX_i+b)-1+\xi_i\bigl\}-\sum_{i=1}^{N}β_i\xi_i
最適化問題を解くとき、次の条件を満たします。
\frac{\partial L(W,b,\xi,α,β)}{\partial W}= W - \sum_{i=1}^{N}α_it_iX_i=0\\
\frac{\partial L(W,b,\xi,α,β)}{\partial b}= -\sum_{i=1}^{N}α_it_i = 0\\
\frac{\partial L(W,b,\xi,α,β)}{\partial W} = C - α_i -β_i = 0
これら三つの式を整理すると以下のようになります。
W =\sum_{i=1}^{N}α_it_iX_i\\
\sum_{i=1}^{N}α_it_i = 0\\
C = α_i + β_i
この三つの式をラグランジュ関数に代入して頑張って計算すると以下のように変数αのみの式になります。
\tilde{L}(α) = \sum_{i=1}^{N}α_i - \frac{1}{2}\sum_{i=1}^{N}\sum_{i=j}^{N}α_iα_jt_it_j{X_i}^TX_j
また、αは0以上であるため、双対問題は以下の条件を満たすαを求めることになります、
max\Bigl\{{\tilde{L}(α) = \sum_{i=1}^{N}α_i - \frac{1}{2}\sum_{i=1}^{N}\sum_{i=j}^{N}α_iα_jt_it_j{X_i}^TX_j\Bigr\}}\\
\sum_{i=1}^{N}α_it_i = 0, \quad 0 \leqq α_i \leqq C, i = 1,2,...N
このように、ソフトマージンにおけるサポートベクトルマシンの双対問題の式を導出することができました。
それではこれから、この双対問題を簡単に解くための手法の一つであるカーネル法についてまとめていきます。
カーネル法について
それではカーネル法について解説していきます。
ここで、Wikipediaからの引用を見ていきましょう。
カーネル法(カーネルほう、英: kernel method)はパターン認識において使われる手法の一つで、 判別などのアルゴリズムに組み合わせて利用するものである。よく知られているのは、サポートベクターマシンと組み合わせて利用する方法である。
パターン認識の目的は、一般に、 データの構造(例えばクラスタ、ランキング、主成分、相関、分類)を見つけだし、研究することにある。この目的を達成するために、 カーネル法ではデータを高次元の特徴空間上へ写像する。特徴空間の各座標はデータ要素の一つの特徴に対応し、特徴空間への写像(特徴写像)によりデータの集合はユークリッド空間中の点の集合に変換される。特徴空間におけるデータの構造の分析に際しては、様々な方法がカーネル法と組み合わせて用いられる。特徴写像としては多様な写像を使うことができ(一般に非線形写像が使われる)、それに対応してデータの多様な構造を見いだすことができる。
カーネル法とは、低次元のデータを高次元に写像して分離する方法だと考えてよいと思います。
厳密には違うのですが、まあここはざっくりとした理解で良いでしょう。
それでは、なぜサポートベクトルマシンでカーネル法が用いられるのかを解説します。
なぜサポートベクトルマシンでカーネル法が用いられているのか
以下の二種類のデータを分類する場合を考えてください。
このような二次元のデータの場合、一次元の直線で二つの種類のデータを分離することができませんね。
このように線形分離不可能な問題に対応するために、このデータを多次元のデータに拡張しましょう。
具体的には、二次元のデータ$X = (x_1, x_2)$を五次元に拡張する場合には以下のような関数を通して写像します。
$$ψ(X) = (x^2_1, x^2_2, x_1x_2, x_1, x_2)$$
このように、データの次元をより高次元に拡張したものを高次元特徴空間と呼び、それに対して最初の入力データの空間を入力空間と呼びます。
上の式をより一般化しましょう。n次元の入力空間のデータを、より高次元のr次元特徴空間に写像する関数を以下のように定義します。
ψ(X) = (φ_1(X), φ_2(X), φ_3(X), ...φ_r(X))
$φ_1(X)$などの関数は、元の関数のデータを組み合わせて変化を加えるという関数です。
このような関数を用いて高次元特徴空間にデータを拡張していくと、ある段階で分離超平面により分離可能なデータになります。というか、究極的には一つ一つのデータを全て別の次元、データがn個あればn次元まで拡張すれば、必ずn-1次元の分離超平面で分離することができます。
つまり、線形分離可能なデータに変化するのです。
後はこの分離超平面を逆写像して元のデータの分離超平面に変換することで、入力空間においてデータを分離する曲線(厳密には入力空間よりも一つ次元が小さな次元に曲線を拡張したもの)を得ることができます。
それでは、高次元特徴空間における最適化問題の式を考えていきましょう。
高次元特徴空間の最適化問題の式を考える前に、入力空間の最適化問題の復習です。
入力空間の最適化問題の復習
max\Bigl\{{\tilde{L}(α) = \sum_{i=1}^{N}α_i - \frac{1}{2}\sum_{i=1}^{N}\sum_{i=j}^{N}α_iα_jt_it_j{X_i}^TX_j\Bigr\}}\\
\sum_{i=1}^{N}α_it_i = 0, \quad 0 \leqq α_i \leqq C, i = 1,2,...N
高次元特徴空間のデータは入力空間のデータ$X_i^T$,$X_j$1を関数$ψ(X)$を用いて写像したものであるので、高次元特徴空間の最適化問題は以下のようになります。
max\Bigl\{{\tilde{L}(α) = \sum_{i=1}^{N}α_i - \frac{1}{2}\sum_{i=1}^{N}\sum_{i=j}^{N}α_iα_jt_it_j{ψ(X)_i}^Tψ(X)_j\Bigr\}}\\
\sum_{i=1}^{N}α_it_i = 0, \quad 0 \leqq α_i \leqq C, i = 1,2,...N
高次元特徴空間において、この最適化問題をといていけばよいことが分かりますね。
カーネル法を用いる
ここで問題になるのは以下の項です。
{ψ(X)_i}^Tψ(X)_j
特徴空間が高次元になればなるほど、この項の計算量がとんでもないことになりますよね。
この部分の計算を簡単にする方法がカーネルトリックと呼ばれる方法です。
以下のようにカーネル関数を定義します。
K(X_i, X_j) = {ψ(X)_i}^Tψ(X)_j
少しごまかしますが、このカーネル関数を用いると$ψ(X)$を直接計算せずに内積を計算することができます。
このように、$ψ(X)$を直接計算せずに内積を計算するためにはある条件を満たす必要があるのですが、なんだかよく分からない 説明するのが大変なので参考となるサイトだけ貼っておきます。
双対問題において$ψ(X)$は内積の形でしか出てこないため、この方法は非常に有用です。
以下のような三つのカーネル関数が用いられます。
ガウスカーネル
K(X_i, X_j) = exp\bigl\{-\frac{||X_i -X_j||^2}{2σ^2}\bigl\}
多項式カーネル
K(X_i, X_j) = (X_i^TX_j + c)^d
シグモイドカーネル
K(X_i, X_j) = tanh(bX_i^TX_j + c)
それでは、実際に多項式カーネルにより内積が簡単に計算できる具体例をみていきましょう。
カーネル法の具体例
以下のような二次元入力空間を三次元特徴空間に写像する関数を考えます。
ψ(X) = ψ(x_1, x_2) = (x_1^2, \sqrt{2}x_1x_2, x_2^2)
この関数を用いると、二つの二次元ベクトルX, Yは以下のようになります。
ψ(X) = ψ(x_1, x_2) = (x_1^2, \sqrt{2}x_1x_2, x_2^2)\\
ψ(Y) = ψ(y_1, y_2) = (y_1^2, \sqrt{2}y_1y_2, y_2^2)
それではこれらの内積を考えていきましょう。
\begin{align}
ψ(X)^Tψ(Y) & = (x_1^2, \sqrt{2}x_1x_2, x_2^2)^T(y_1^2, \sqrt{2}y_1y_2, y_2^2)\\
&=x_1^2y_1^2 + 2x_1y_1x_2y_2 + x_2^2y_2^2\\
&= (x_1y_1 + x_2y_2)^2\\
&=((x_1,x_2)^T(y_1,y_2))^2\\
&=(X^TY)^2
\end{align}
このように、$ψ(X)^Tψ(Y)$を直接計算せずに、元のベクトルの内積を二乗することで、$ψ(X)^Tψ(Y)$を計算することができます。
カーネル法についてもう少し詳しく知りたい方はこちらの記事を参考にしてください。
それではこれから、サポートベクトルマシンの実装についてまとめていきます。
サポートベクトルマシンの実装
分類問題:ハードマージン
線形分離可能なデータを分離するsvmを実装していきます。
用いるデータはiris(アヤメ)データセットです。
iris(アヤメ)データセットについて
irisデータは、アヤメという花の品種のデータです。
アヤメの品種であるSetosa、Virginica、Virginicaの3品種に関するデータが50個ずつ、全部で150個のデータです。
実際に中身を見ていきましょう。
from sklearn.datasets import load_iris
import pandas as pd
iris = load_iris()
iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)
print(iris_df.head())
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2
iris.feature_namesに各々のカラム名が格納されているので、それをpandasのDataframeの引数に渡すことで上のようなデータを出力できます。
Sepal Lengthはがく弁の長さが、Sepal Widthにはがく弁の幅が、Petal lengthには花びらの長さが、Petal Widthには花びらの幅のデータが格納されています。
以下のようにすれ正解ラベルを表示できます。
print(iris.target)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
このように、アヤメの品種であるsetosa、versicolor、virginicaをそれぞれ0, 1, 2としています。
アヤメのデータについての説明はここまでです。
実装
以下のコードでデータセットを作成しましょう。
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
import mglearn
iris = load_iris()
X = iris.data[:100, 2:]
Y = iris.target[:100]
print(X.shape)
print(Y.shape)
(100, 2)
(100,)
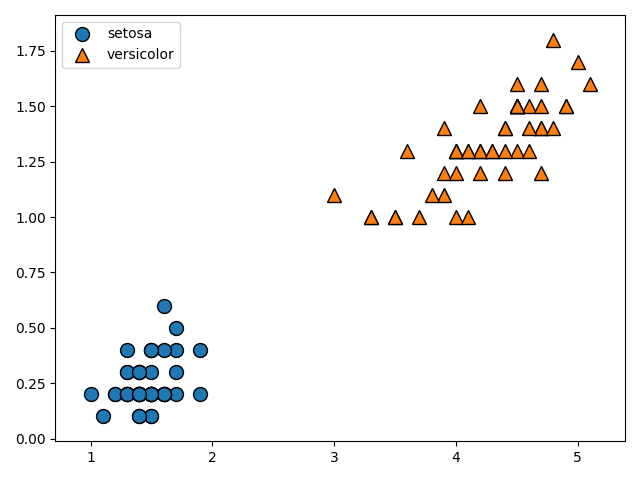
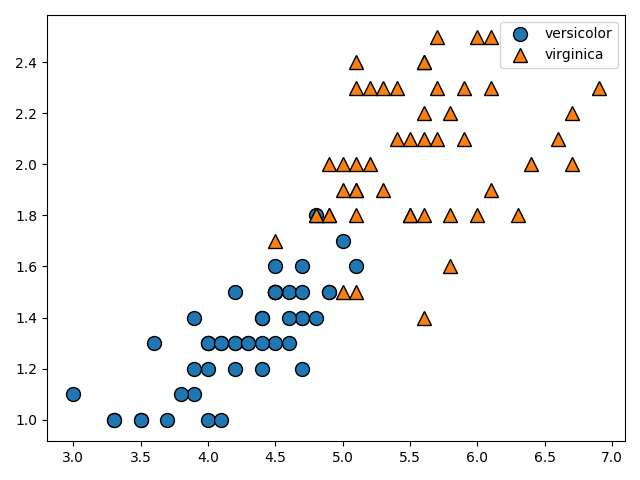
今回はsetosa、versicolorのpetal lengthとpetal widthのデータを用いて分類を行います。
以下のコードでデータの描画を行います。
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.legend(['setosa', 'versicolor'], loc='best')
plt.show()
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)のコードは第一引数をX軸、第二引数にY軸、第三引数に正解ラベルをとって、scatterプロットを行います。
loc='best'により、凡例がグラフの邪魔にならない位置にくるように調整しています。
上のデータから、明らかに直線で分離できることが分かりますね。むしろ簡単すぎるくらいです。
次のコードでモデルを作成しましょう。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, stratify=Y, random_state=0)
svm = LinearSVC()
svm.fit(X_train, Y_train)
モデルの作成自体はこのコードで終わりです。簡単ですね。
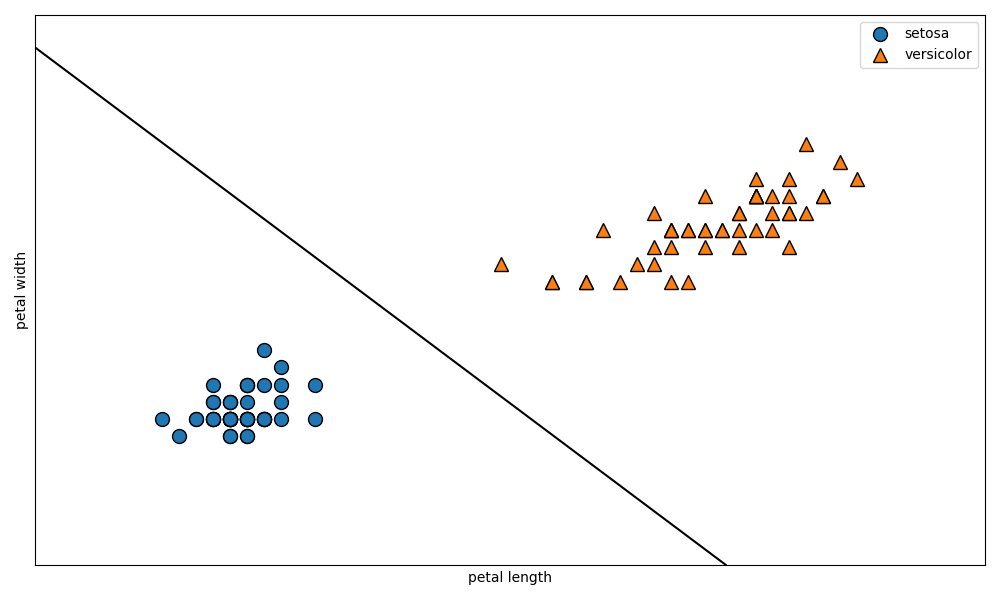
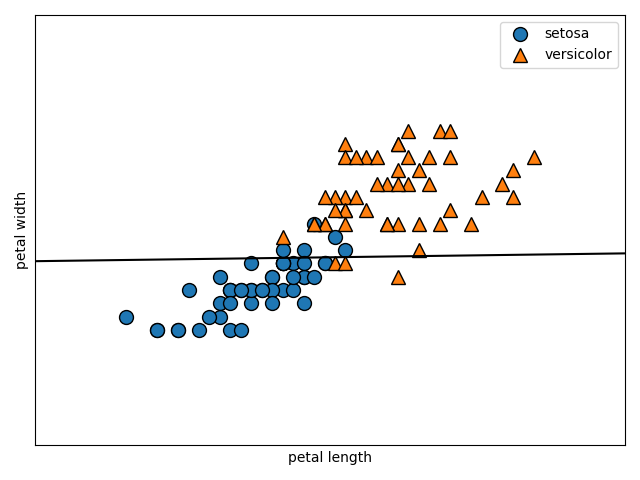
以下のコードでモデルがどのような形になったのかを図示しましょう。
plt.figure(figsize=(10, 6))
mglearn.plots.plot_2d_separator(svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(['setosa', 'versicolor'], loc='best')
plt.show()
しっかりとデータを分ける境界線が作成されていることが確認できますね。
mglearn.plots.plot_2d_separator(svm, X)の部分は少し分かりにくいと思うので解説します。定義となるコードを確認しましょう。
plot_2d_separator(classifier, X, fill=False, ax=None, eps=None, alpha=1,cm=cm2, linewidth=None, threshold=None,linestyle="solid"):
第一引数に分類モデルを渡して、第二引数に元のデータを渡すと境界線を引いてくれる関数ですね。
ここまでで、線形分離可能な問題におけるsvmのモデルの実装は終了です。
分類問題: ソフトマージン
今回はソフトマージンの問題について取り扱います。
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.svm import LinearSVC
from sklearn.datasets import load_iris
import mglearn
iris = load_iris()
X = iris.data[50:, 2:]
Y = iris.target[50:] - 1
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.legend(['versicolor', 'virginica'], loc='best')
plt.show()
今度はversicolorとverginicaのpetal lengthとpetal widthについてのデータをプロットしています。
完全に線形分離することは不可能な問題ですね。
ここでソフトマージンの式を復習です。導出はこちらの記事を参考にしてください。
min_{W, \xi}\Bigl\{\frac{1}{2}||W||^2 + C\sum_{i=1}^{N} \xi_i\Bigr\} \quad \quad
t_i(W^TX_i + b)\geq 1 - \xi_i\\
\xi_i = max\Bigl\{0, M - \frac{t_i(W^TX_i + b)}{||W||}\Bigr\}\\
i = 1, 2, 3, ... N
データがマージンの内側に入り込んでしまうので、$ C\sum_{i=1}^{N} \xi_i$の項により制限を緩めているのでしたね。
このCの値はskleaarnにおいて、デフォルトで1.0になっています。この数値を変化させて、図がどう変わるのか確認してみましょう。以下のコードで、引数に与えたモデルの境界線をプロットする関数を定義します。
def make_separate(model):
mglearn.plots.plot_2d_separator(svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.xlabel('petal length')
plt.ylabel('petal width')
plt.legend(['setosa', 'versicolor'], loc='best')
plt.show()
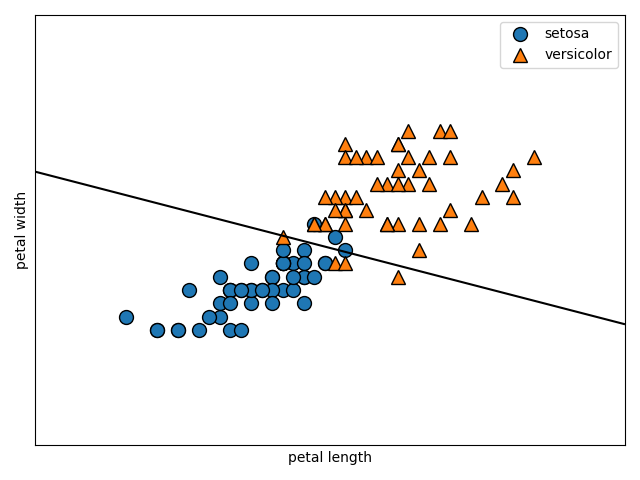
以下のコードで図を描画しましょう。C=0.1とします。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, stratify=Y, random_state=0)
svm = LinearSVC(C=0.1)
svm.fit(X_train, Y_train)
make_separate(svm)
print(svm.score(X_test, Y_test))
0.96
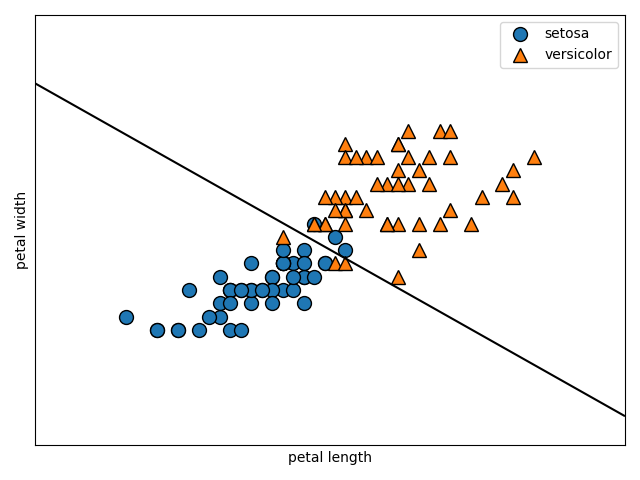
次はC=1.0です。
svm = LinearSVC(C=1.0)
svm.fit(X_train, Y_train)
make_separate(svm)
print(svm.score(X_test, Y_test))
1.0
次はC=100です。
svm = LinearSVC(C=100)
svm.fit(X_train, Y_train)
make_separate(svm)
print(svm.score(X_test, Y_test))
1.0
適切なCを設定するのが大切ですね。色々変えながら様子を見ていくのがよさそうです。
ここまででソフトマージンの実装は終了です。
それではこれから、カーネル法を用いたときの実装と用いなかったときの実装についてまとめていきます。
カーネル法を用いずに実装
今回は線形分離不可能な問題をカーネル法を用いずに分類していきます。
ここでは、カーネル関数を使わない方法を、カーネル法を使わないと定義しています。
以下のコードでデータを準備して、図示しましょう。
import mglearn
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
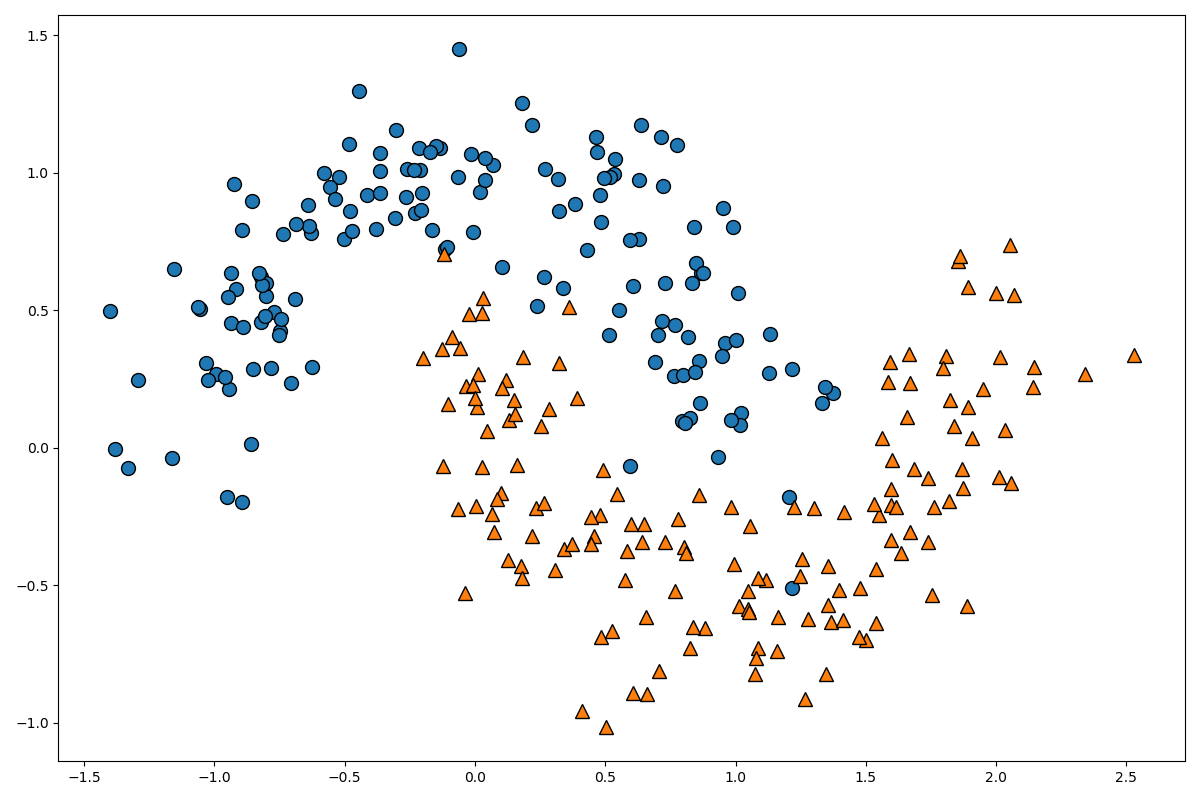
moons = make_moons(n_samples=300, noise=0.2, random_state=0)
X = moons[0]
Y = moons[1]
plt.figure(figsize=(12, 8))
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.plot()
plt.show()
make_moonsは、二次元の月のような形をしたデータを作成する関数です。
サンプル数とノイズを設定することができます。
図を見て頂ければ分かりますが、明らかに線形分離不可能ですよね。
この線形分離不可能なデータを線形分離可能なデータに変形するために、この入力空間のデータを高次元特徴空間のデータに写像しましょう。
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, stratify=Y, random_state=0)
poly = PolynomialFeatures(degree=2)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.fit_transform(X_test)
これで、入力空間のデータを高次元特徴空間に写像することができました。
どのようなデータに写像されたか確認しましょう。
print(poly.get_feature_names())
print(X_train_poly.shape)
['1', 'x0', 'x1', 'x0^2', 'x0 x1', 'x1^2']
(225, 6)
このような形で、二次元入力空間が六次元特徴空間に拡張されています。
次のコードでデータを標準化します。
scaler = StandardScaler()
X_train_poly_scaled = scaler.fit_transform(X_train_poly)
X_test_poly_scaled = scaler.fit_transform(X_test_poly)
データの標準化とは、全てのデータに対して平均を引いた後に標準偏差で割ることで、データの平均を0、分散を1にすることです。
こちらの記事に分かりやすく書いていたので、参考にしてください。
それでは、次のコードでモデルを実装して評価します。
lin_svm = LinearSVC()
lin_svm.fit(X_train_poly_scaled, Y_train)
print(lin_svm.score(X_test_poly_scaled, Y_test))
0.84
ちょっと低いですね。もう少し高次元に写像しましょう。
しかし、高次元に写像して標準化するという処理が面倒くさいので、Pipelineというものを使用しましょう。
poly_scaler_svm = Pipeline([
('poly', PolynomialFeatures(degree=3)),
('scaler', StandardScaler()),
('svm', LinearSVC())
])
poly_scaler_svm.fit(X_train, Y_train)
print(poly_scaler_svm.score(X_test, Y_test))
0.9733333333333334
このように、Pipelineを用いると、データを高次元に写像して、標準化して、svmモデルに入れるという作業を簡略化して書くことができます。degree=3にすることで、より高次元の特徴空間に写像しています。
精度はかなり良いですね。高次元に写像するとかなり効果的です。
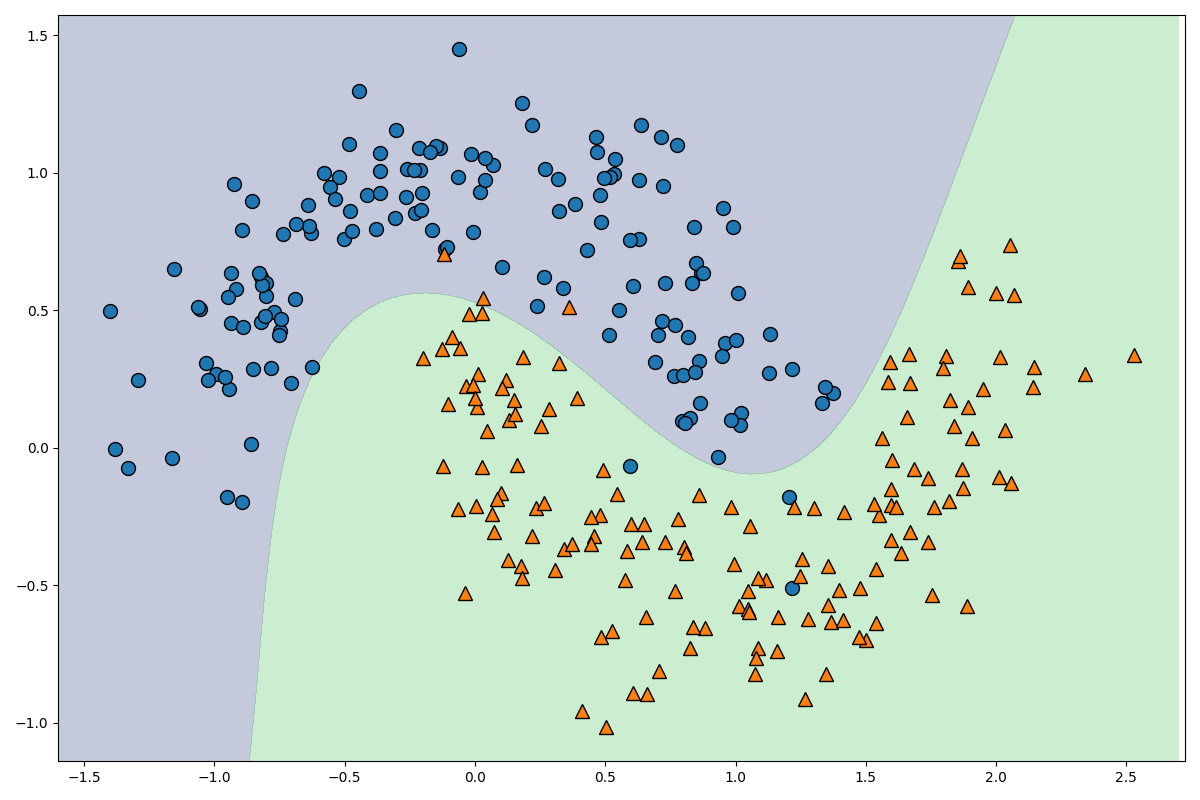
次は、この図を描画してみましょう。以下のコードです。
_x0 = np.linspace(-1.5, 2.7, 100)
_x1 = np.linspace(-1.5, 1.5, 100)
x0, x1 = np.meshgrid(_x0, _x1)
X = np.hstack((x0.ravel().reshape(-1, 1), x1.ravel().reshape(-1, 1)))
y_decision = model.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_decision, levels=[y_decision.min(), 0, y_decision.max()], alpha=0.3)
plt.figure(figsize=(12, 8))
mglearn.discrete_scatter(X[:, 0], X[:, 1], Y)
plt.show()
なかなかきれいな線が引けていることが確認できましたね。それではコードを解説します。
_x0 = np.linspace(-1.5, 2.7, 100)
_x1 = np.linspace(-1.5, 1.5, 100)
x0, x1 = np.meshgrid(_x0, _x1)
ここの部分のコードで格子点を作成しています。こちらの記事に分かりやすく書いてあるので、参考にしてください。
np.linspaceは第一引数に始点、第二引数に終点、第三引数に点の数を指定して、numpyのarrayを作成します。それをnp.meshgridに渡すことで、100×100の格子点を作成しています。
X = np.hstack((x0.ravel().reshape(-1, 1), x1.ravel().reshape(-1, 1)))
(x0.ravel()により、100×100のarrayを一次元配列に変換した後、reshape(-1, 1)により二次元の10000×1の行列に変換し、np.hstackによりaxis=1の水平方向に対して結合しています。つまり、Xは10000×2の行列になっています。
y_decision = model.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_decision, levels=[y_decision.min(), 0, y_decision.max()], alpha=0.3)
model.decision_function(X)により10000個の格子点と分離超平面との距離を求めて、それを100×100のデータに変換しています。
plt.contourfは等高線を図示する関数で、levelsにどの部分で色を変化させるかを指定できます。
以上でカーネル法を使わない実装は終了です。
カーネル法を用いた実装
それではカーネル法を用いて実装を行っていきます。
データを準備しましょう。ここまでは同じです。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
moons = make_moons(n_samples=300, noise=0.2, random_state=0)
X = moons[0]
Y = moons[1]
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, stratify=Y, random_state=0)
次のコードでモデルを実装しましょう。
karnel_svm = Pipeline([
('scaler', StandardScaler()),
('svm', SVC(kernel='poly', degree=3, coef0=1))
])
karnel_svm.fitX_train, Y_train()
SVCのkarnel引数にpolyを指定することで、多項式カーネルを指定し、degree=3を指定することで三次元までの写像を考えることができます。
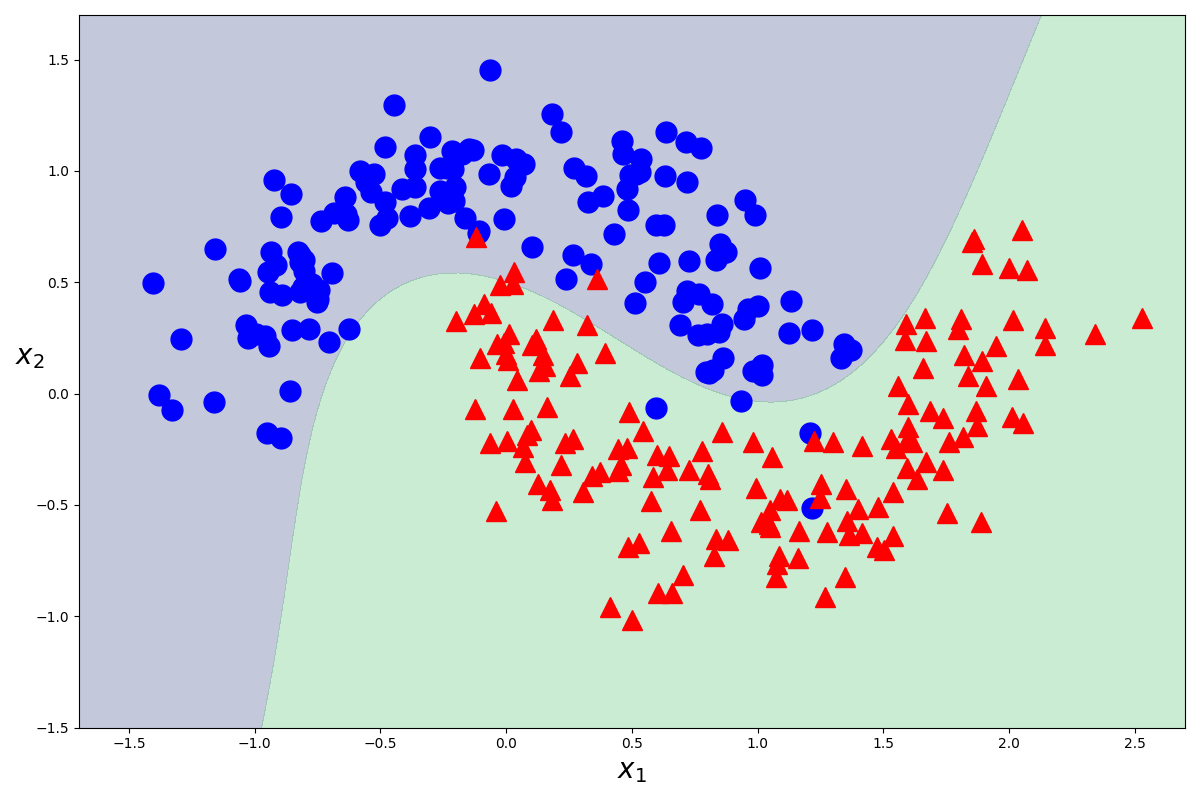
これでモデルの作成ができました。次は、このモデルを図示してみましょう。また同じことをするんですが、面倒くさいので関数にします。
def plot_decision_function(model):
_x0 = np.linspace(-1.7, 2.7, 100)
_x1 = np.linspace(-1.5, 1.7, 100)
x0, x1 = np.meshgrid(_x0, _x1)
X = np.hstack((x0.ravel().reshape(-1, 1), x1.ravel().reshape(-1, 1)))
y_decision = model.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_decision, levels=[y_decision.min(), 0, y_decision.max()], alpha=0.3)
def plot_dataset(x, y):
plt.plot(x[:, 0][y == 0], x[:, 1][y == 0], 'bo', ms=15)
plt.plot(x[:, 0][y == 1], x[:, 1][y == 1], 'r^', ms=15)
plt.xlabel('$x_1$', fontsize=20)
plt.ylabel('$x_2$', fontsize=20, rotation=0)
plt.figure(figsize=(12, 8))
plot_decision_function(karnel_svm)
plot_dataset(X, Y)
plt.show()
mglearnでプロットしても良かったのですが、今回はplt.plotでプロットしました。Y=0となるものを青色の丸で、Y=1となるものを赤色の三角で描画しています。
図から分かるように、カーネル法を使っても使わなくても同じ結果が返ってきます。しかし、カーネル法を用いた方が内部的に計算がかなり簡単になっているので、できるだけカーネル法を使った方が良い気がします。
どのように簡単になるのかはこちらの記事を参考にしてください。
終わりに
ここまでお付き合い頂きありがとうございました。
非常に長い記事になりました。ここまで読んで下さり本当にありがとうございます。
お疲れさまでした。