はじめに
確率論や統計学を勉強したら色々な確率分布が出られて、どんな分布がどんな状況で使うか迷ってしまうくらいいっぱいあるのですね。
自然に発生する現象における確率変数の値はどの確率分布で説明できるかは現象によって色々違うのです。
この記事では各種の確率分布が発生する現象をpythonでシミュレーションして分布を描いてみます。
実は分布の由来がわからなくても、scipyのscipy.statsモジュールを使ったら色んな確率分布を簡単に実装できますが、まずはどんな事情でどうやってこんな分布ができるかわかることに意味があると思います。
なのでここでpythonのrandomモジュールとnumpyだけで実装します。
一つずつランダムする時はrandomモジュールを、一気にたくさんランダムする時はnumpyを使います。(グラフはmatplotlibで)
その後scipy.statsでも使って結果を比較してみます。その分布の意味の理解が間違いなければ結果は一致するはずです。
scipy.statsの使い方についてはこの記事など https://qiita.com/supersaiakujin/items/71540d1ecd60ced65add 色んな記事に書いてあるのでは詳しく説明しません。
基本的に確率分布は離散型確率分布と連続型確率分布に二種類に分けられ、実装方法はちょっと違います。
主な違いとして例えば、離散型確率分布は確率質量関数(PMF)で確率分布を示するのに対し、連続型確率分布は確率密度関数(PDF)で確率分布を示します。
ここで説明する確率分布は
離散型確率分布
連続型確率分布
離散型確率分布
二項分布
成功か失敗のいずれかという結果になる実験をする時、成功する回数の確率分布は二項分布になるのです。
確率質量関数は
P(x) = C(n,x)p^x(1-p)^{n-x}
p=成功する確率
n=行なった回数
$C(n,x)$はn個からx個を選ぶ組合せ関数
例えば、あるゲームではあるモンスターを倒すと確率pでアイテムをドロップし、もしn匹倒したらどれくらいアイテムがドロップするか、という話でドロップの数は二項分布になるはずです。
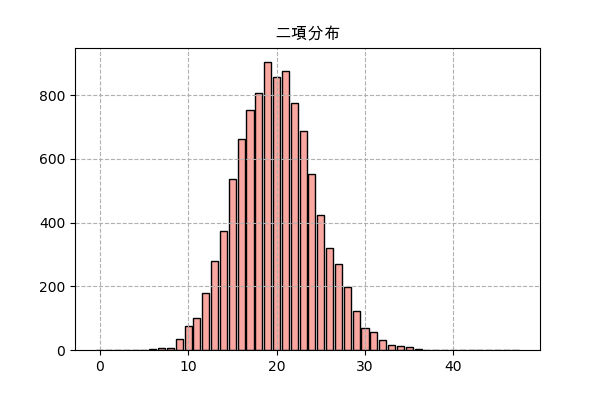
実際にランダムして結果を見てみます。ここでn=2000、p=0.01で、サンプリング回数は10000にします。
import random
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats
# ここでまず全部使うモジュールをimportしておきます。
n_sampl = 10000 # サンプリング回数
n = 2000 # 倒すモンスターの数
p = 0.01 # アイテムがドロップする確率
n_drop = [] # 各ドロップ数の回数
for _ in range(n_sampl):
# n個ランダムをしてp以下かどうか判断
drop = np.random.random(n)<=p
n_drop.append(drop.sum()) # ドロップ数を格納
y = np.bincount(n_drop) # 各ドロップ数の回数を数える
x = np.arange(len(y))
# 棒グラフを描く
plt.title('二項分布',family='Arial Unicode MS')
plt.bar(x,y,color='#f9a7a0',ec='k')
plt.grid(ls='--')
plt.savefig('binom.png',dpi=100)
plt.close()
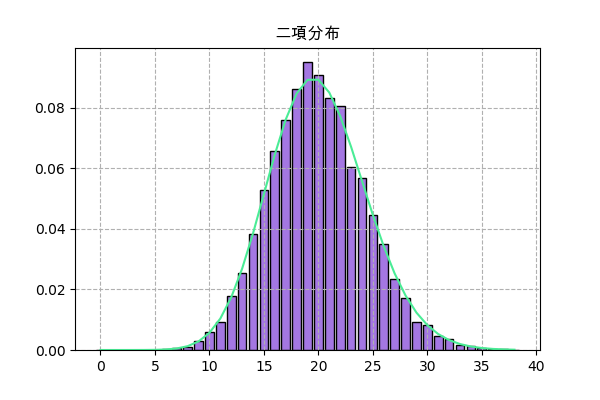
次はscipy.statsでの実装。ここで.rvs()を使ってランダムして、.pmf()を使ってグラフを書きます。
f = scipy.stats.binom(n,p)
plt.title('二項分布',family='Arial Unicode MS')
h = np.bincount(f.rvs(10000))
x = np.arange(len(h))
plt.bar(x,h/n_sampl,color='#a477e2',ec='k')
plt.plot(x,f.pmf(x),'#4aec96')
plt.grid(ls='--')
plt.savefig('binom2.png',dpi=100)
plt.close()
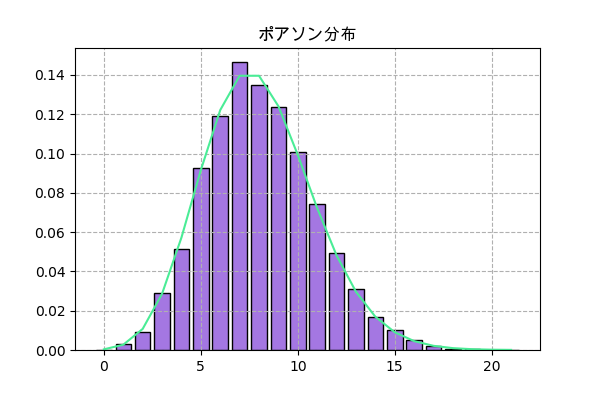
.rvs()で描いた分布は.pmf()のグラフと大体一致しますし、上の図とも一致します。だだし、ここでは全部合わせて1になるようにnサンプリング回数で割ります。
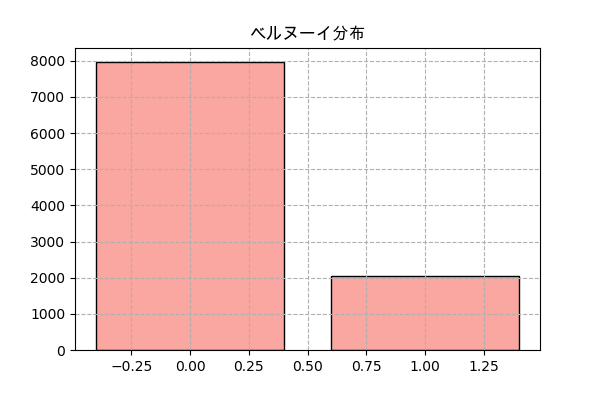
ベルヌーイ分布
二項分布でn=1の場合、ベルヌーイ分布と呼ばれます。
二項分布の確率質量関数にn=1にすると
P(x) = p^x(1-p)^{1-x}
となります。1回の実行なので、結果は0(成功)と1(失敗)しかない。
コードは二項分布より簡単になります。
n_sampl = 10000
p = 0.2 # アイテムがドロップする確率
n_drop = [] # 各ドロップ数の回数(0か1)
for _ in range(n_sampl):
n_drop.append(random.random()<=p) # ランダム値がp以下かどうか
y = np.bincount(n_drop)
x = np.arange(len(y))
plt.title('ベルヌーイ分布',family='Arial Unicode MS')
plt.bar(x,y,color='#f9a7a0',ec='k')
plt.grid(ls='--')
plt.savefig('bernulli.png',dpi=100)
plt.close()
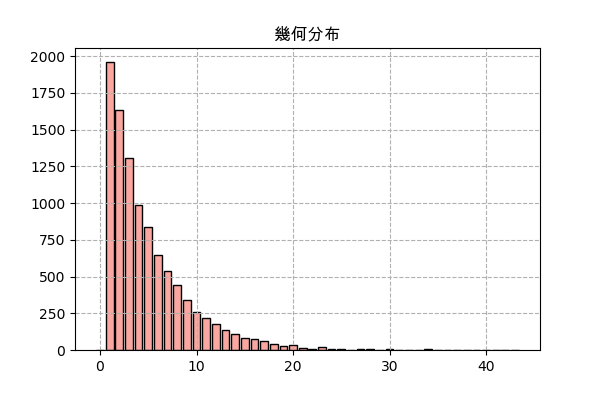
幾何分布
二項分布と同じように、幾何分布も成功と失敗のある実験を行なう時に発生する分布ですが、幾何分布で考慮するのは成功するまでの回数の分布です。
ある成功か失敗のいずれかになる実行を、成功するまでの回数の分布は幾何分布になるということです。
成功する確率はpだとしたら、成功するまでの回数の確率質量関数は
P(x) = p(1-p)^{x-1}
例えば、ゲームで確率pでアイテムがドロップするモンスターが、何匹倒したらドロップするか、その回数の確率分布は幾何分布。
ランダムするものは二項分布の場合と同じですが、今回は倒すモンスターの数が固定ではなく、一回成功するまで繰り返すということになります。
n_sampl = 10000 # サンプリング回数
p = 0.2 # ドロップする確率
kaime_drop = [] # 何回目でドロップするかという結果を格納するリスト
for _ in range(n_sampl):
n_kai = 1 # 倒したモンスターの数
# 成功するまで繰り返す
while(random.random()>p):
n_kai += 1
# 成功した後で倒したモンスターの数を格納
kaime_drop.append(n_kai)
y = np.bincount(kaime_drop) # 倒したモンスターの数を数える
x = np.arange(len(y))
# 棒グラフを描く
plt.title('幾何分布',family='Arial Unicode MS')
plt.bar(x,y,color='#f9a7a0',ec='k')
plt.grid(ls='--')
plt.savefig('geom.png',dpi=100)
plt.close()
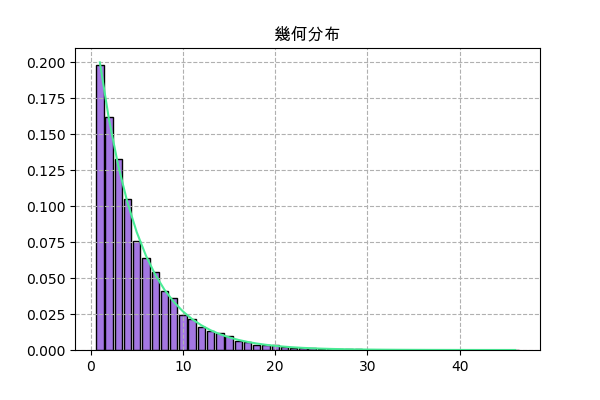
scipyで実装
f = scipy.stats.geom(p)
plt.title('幾何分布',family='Arial Unicode MS')
h = np.bincount(f.rvs(10000))
x = np.arange(1,len(h))
h = h[1:]
plt.bar(x,h/n_sampl,color='#a477e2',ec='k')
plt.plot(x,f.pmf(x),'#4aec96')
plt.grid(ls='--')
plt.savefig('geom2.png',dpi=100)
plt.close()
負の二項分布
幾何分布と似て、負の二項分布も実行する回数の分布ですが、一回成功するだけで満足するのではなく、ある特定の成功回数まで実行する回数を考えることになります。
確率質量関数は
P(x) = C(k+r-1,k)(1-p)^rp^k
p=成功する確率
r=達成したい回数
rが1だったら幾何分布になります。
例えば、確率pでアイテムをドロップするモンスターから、アイテムをr個欲しい場合、どれくらい倒す必要があるか、という例題。
やり方のは幾何分布よりちょっと複雑になりますが、ほぼ同じ。
n_sampl = 10000
p = 0.2 # ドロップする確率
r = 4 # 欲しい成功回数
kaime_drop = []
for _ in range(n_sampl):
n_kai = 0 # 倒したモンスターの回数
n_drop = 0 # ドロップ回数
# 何回も繰り返しモンスターを倒す
while(n_drop<r):
# ドロップかどうか
if(random.random()<=p):
n_drop += 1
n_kai += 1
# r回ドロップした後、倒したモンスターの回数を格納
kaime_drop.append(n_kai)
y = np.bincount(kaime_drop)
x = np.arange(len(y))
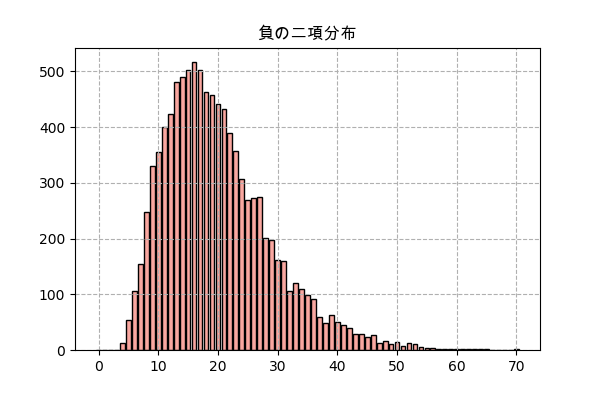
plt.title('負の二項分布',family='Arial Unicode MS')
plt.bar(x,y,color='#f9a7a0',ec='k')
plt.grid(ls='--')
plt.savefig('nbinom.png',dpi=100)
plt.close()
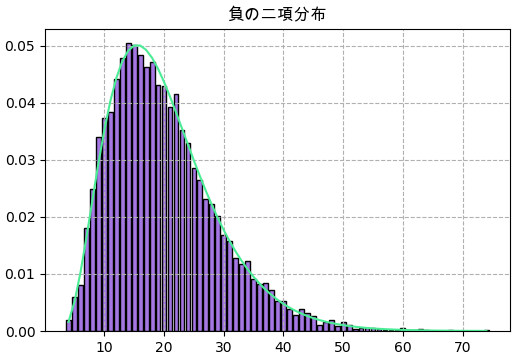
scipyで実装
f = scipy.stats.nbinom(r,p)
plt.title('負の二項分布',family='Arial Unicode MS')
y = np.bincount(f.rvs(10000))
x = np.arange(len(h))
plt.bar(x+r,y/n_sampl,color='#a477e2',ec='k')
plt.plot(x+r,f.pmf(x),'#4aec96')
plt.grid(ls='--')
plt.savefig('nbinom2.png',dpi=100)
plt.close()
ポアソン分布
ある出来事がどんな時でも同じ確率で起きる場合、ある特定の区間の中に起きる回数はポアソン分布となります。
確率質量関数は
P(x) = \frac{λ^x e^{-λ}}{x!}
λ=ある特定の区間の中で起きる平均回数
例えば、あるゲームでモンスターが大体一時間にλ回現れるとしたら、実際に各一時間の間に現れる回数。
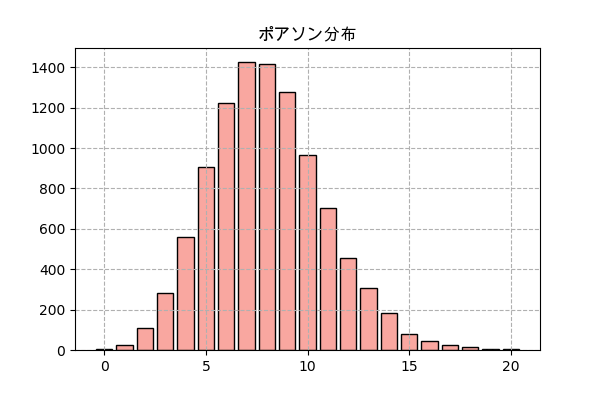
n = 10000 # 分ける時間の区間の数
λ = 8 # ある時間にある平均回数
# 起きる時間をランダム
jikan = np.random.uniform(0,n,n*λ)
# 1時間単位に分けて、各区間の中の回数を数える
kaisuu = np.bincount(jikan.astype(int))
# 回数の分布を見るために、どれくらいの回数が何個あるか数える
y = np.bincount(kaisuu)
x = np.arange(len(y))
plt.title('ポアソン分布',family='Arial Unicode MS')
plt.bar(x,y,color='#f9a7a0',ec='k')
plt.grid(ls='--')
plt.savefig('poisson.png',dpi=100)
plt.close()
やや複雑ですが、要するにまずは起こる時間をランダムします。ある区間でλ回くらい起きるというのだから、ランダムの範囲は分ける区間の数(n)と同じにして、ランダム回数はnλにします。
その後、np.bincount()で各区間に起きる回数を数えます。
そして全部の区間の起きる回数の分布を数えるために又np.bincount()を使います。
scipyでの実装
f = scipy.stats.poisson(λ)
plt.title('ポアソン分布',family='Arial Unicode MS')
h = np.bincount(f.rvs(10000))
x = np.arange(len(h))
plt.bar(x,h/n,color='#a477e2',ec='k')
plt.plot(x,f.pmf(x),'#4aec96')
plt.grid(ls='--')
plt.savefig('poisson2.png',dpi=100)
plt.close()
連続型確率分布
ある特定の数字だけの確率を持つ離散型確率分布とは違って、連続値型確率分布の場合ある特定の数字になる確率が0になり、代わりに求まるのは値が各範囲にあるという確率なので、確率密度関数で確率分布を表示することになります。
連続一様分布
連続一様分布は、ある範囲の中だけで同じような確率分布を持つという簡単な分布です。
分布範囲がaからbまでだとしたら、x∈[a,b]の確率密度関数は
f(x) = \frac{1}{b-a}
範囲外では$f(x)=0$。
簡単にnp.random.uniformやrandom.uniformで実装できます。
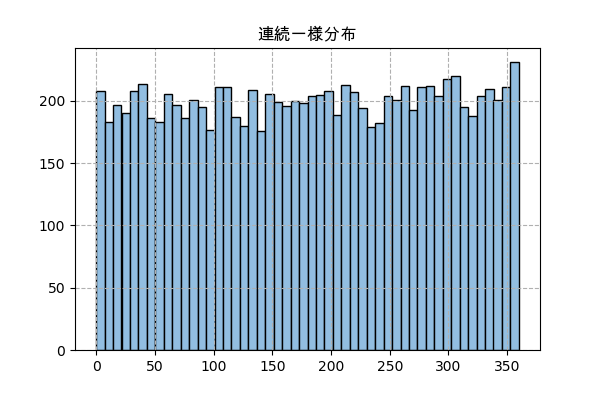
例えば、ある区間のないルーレットの話です。そのルーレットにボールを投げたら普通に考えると、0度から360度まで同じ確率に止まるはずです。
n_sampl = 10000
a = 0 # 最小限
b = 360 # 最大限
x = np.random.uniform(a,b,n_sampl) # ランダム
# ヒストグラムを書く
plt.title('連続一様分布',family='Arial Unicode MS')
plt.hist(x,50,color='#92bee1',ec='k')
plt.grid(ls='--')
plt.savefig('uniform.png',dpi=100)
plt.close()
連続一様分布は場合、np.bincount()で数を数えて棒グラフを描くのではなく、plt.hist()で密度を示すヒストグラムにします。
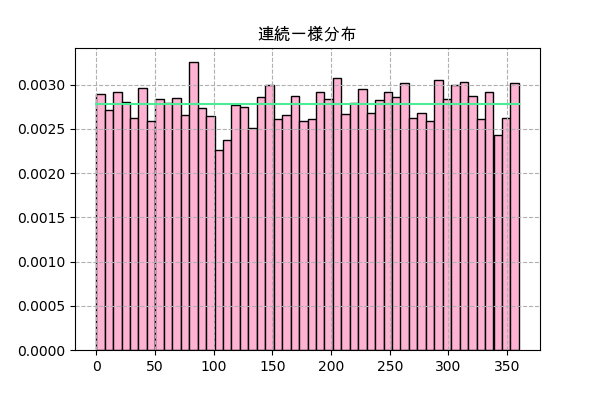
scipyにはscipy.stats.uniformがありますが、.rvs()を使う場合はあまりnp.random.uniformと変わらないようです。
scipy.statsで分布関数のメソッドは離散型とは違って、連続型は.pmf()ではなく、.pdf()になります。
plt.hist()で.rvs()の分布を描く時density=Trueにしたら全部のサンプル数で割られて.pdf()の値と一致することになります。
f = scipy.stats.uniform(a,b)
plt.title('連続一様分布',family='Arial Unicode MS')
_,h,_ = plt.hist(f.rvs(10000),50,color='#ffb3d3',ec='k',density=True)
x = np.linspace(h.min(),h.max(),101)
plt.plot(x,f.pdf(x),'#4aec96')
plt.grid(ls='--')
plt.savefig('uniform2.png',dpi=100)
plt.close()
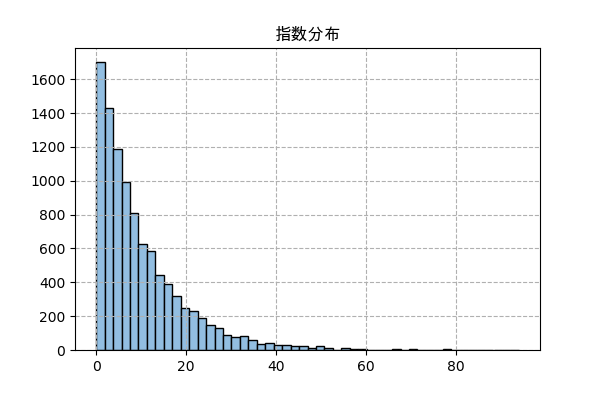
指数分布
指数分布はポアソン分布が発生する同時に発生する分布です。
ある出来事がある時間の中でいつでも起これるとしたら、毎回起きる間の時間の分布は指数分布になります。
確率密度関数は
f(x) = λe^{-λx}
ポアソン分布の場合と同じく、λはある特定の区間の中に起きる平均回数
例えば、モンスターが一時間でλ回現れるとしたら、一匹が現れた後、どれくらい待ったら次は現れるか、という話。
やり方はポアソン分布と似ていますが、指数分布の方が簡単に見えます。
n = 10000 # 時間の長さ
λ = 10 # 一時間で起きる平均回数
t = np.random.uniform(0,n*λ,n) # 起きる時間をランダム
t = np.sort(t) # 並べ替え
x = t[1:]-t[:-1] # 時間の差
# ヒストグラムを描く
plt.title('指数分布',family='Arial Unicode MS')
plt.hist(x,50,color='#92bee1',ec='k')
plt.grid(ls='--')
plt.savefig('expon.png',dpi=100)
plt.close()
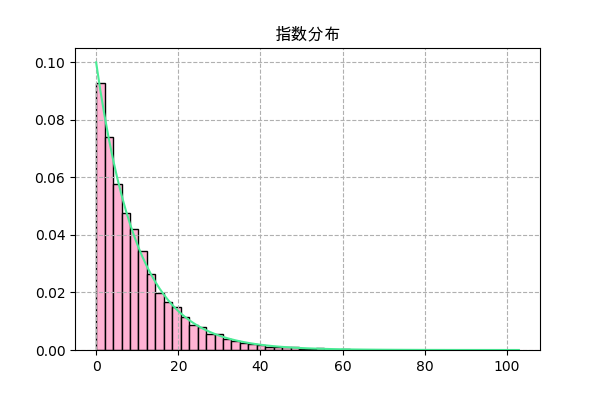
scipyで実装
f = scipy.stats.expon(0,λ)
plt.title('指数分布',family='Arial Unicode MS')
_,h,_ = plt.hist(f.rvs(10000),50,color='#ffb3d3',ec='k',density=True)
x = np.linspace(h.min(),h.max(),101)
plt.plot(x,f.pdf(x),'#4aec96')
plt.grid(ls='--')
plt.savefig('expon2.png',dpi=100)
plt.close()
正規分布
正規分布、またはガウス分布は一番起こりやすい分布なので、ありふれた分布で世界最強。
正規分布は色んな状況で発生できますが、今回は中心極限定理によって発生する正規分布を試します。
中心極限定理によると、あるたくさんの確率変数の平均値を取ったら、(元々の分布はどうであれ)その平均値の確率分布は正規分布になるということです。
正規分布の確率密度関数は
f(x) = \frac{1}{\sqrt{2πσ^2}}e^{\left(-\frac{(x-μ)^2}{2σ^2}\right)}
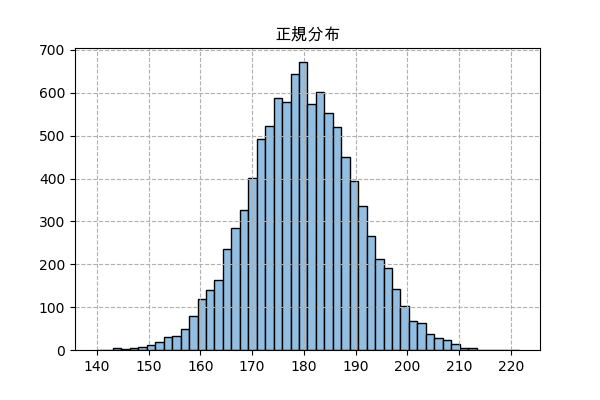
連続一様分布の例題と同じように無限ルーレットで試しますがね今回は100回の結果の平均値の分布を見ます。
n_sampl = 10000
n = 100
a,b = 0,360
x = np.random.uniform(a,b,[n_sampl,n]).mean(1)
plt.title('正規分布',family='Arial Unicode MS')
plt.hist(x,50,color='#92bee1',ec='k')
plt.grid(ls='--')
plt.savefig('norm.png',dpi=100)
plt.close()
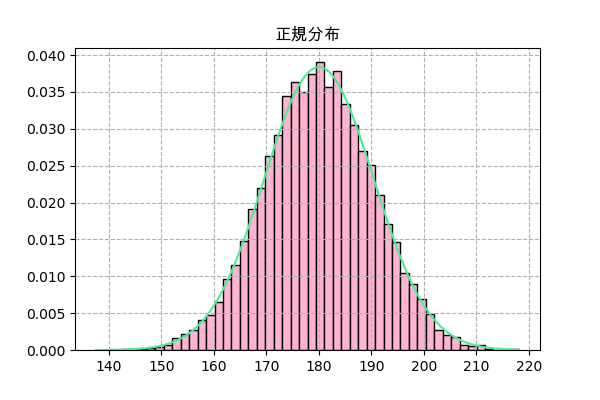
次はscipy.statsで正規分布を実装しますが、まずは平均値と標準偏差を合わせるために計算が必要です。
連続一様分布の平均値は$\frac{b+a}{2}$で、標準偏差は$\frac{(b-a)^2}{12}$ですが、大数の法則$n$によると、回試した結果の標準偏差は$\frac{1}{\sqrt{n}}$となります。
μ = (a+b)/2 # 平均値μを計算
σ = np.sqrt((b-a)**2/12/n) # 標準偏差σを計算
f = scipy.stats.norm(μ,σ)
plt.title('正規分布',family='Arial Unicode MS')
_,h,_ = plt.hist(f.rvs(10000),50,color='#ffb3d3',ec='k',density=True)
x = np.linspace(h.min(),h.max(),101)
plt.plot(x,f.pdf(x),'#4aec96')
plt.grid(ls='--')
plt.savefig('norm2.png',dpi=100)
plt.close()
カイ二乗分布
正規分布に従う確率変数をk回実行してみしたら、その二乗和
\sum_{i=1}^{k}x_i^2
確率密度関数は
f(x) = \frac{x^{k/2-1}e^{-x/2}}{\,2^{k/2} \Gamma(k/2)}
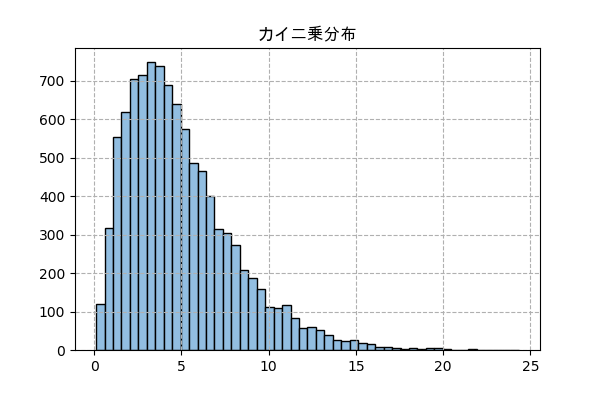
正規分布のランダムから始める実装
n_sampl = 10000
k = 5
randn = np.random.randn(n_sampl,k)
x = (randn**2).sum(1)
plt.title('カイ二乗分布',family='Arial Unicode MS')
plt.hist(x,50,color='#92bee1',ec='k')
plt.grid(ls='--')
plt.savefig('chi2.png',dpi=100)
plt.close()
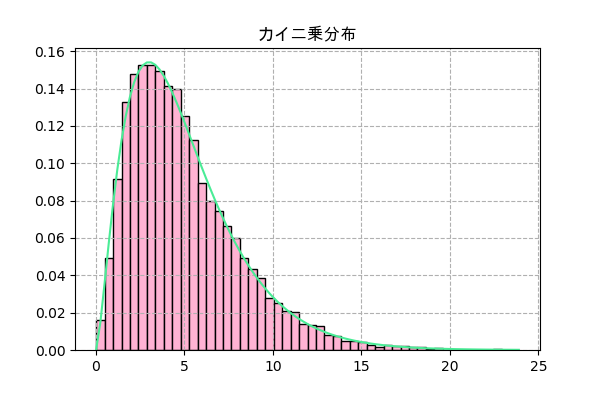
scipyで実装
f = scipy.stats.chi2(k)
plt.title('カイ二乗分布',family='Arial Unicode MS')
_,h,_ = plt.hist(f.rvs(10000),50,color='#ffb3d3',ec='k',density=True)
x = np.linspace(h.min(),h.max(),101)
plt.plot(x,f.pdf(x),'#4aec96')
plt.grid(ls='--')
plt.savefig('chi22.png',dpi=100)
plt.close()
ベータ分布
ベータ分布はベイズ確率を考える時に発生する確率分布で、かなり他の分布より複雑です。
ある出来事の発生する確率が不明で、成功する回数からその確率を推測する場合、その確率の確率分布はベータ分布になります。
確率密度関数は
f(x) = \frac{x^{α-1}(1-x)^{β-1}}{B(α,β)}
α-1=成功の回数
β-1=失敗の回数
Bはベータ関数
詳しくは『完全独習 ベイズ統計学入門』という本を参考に。
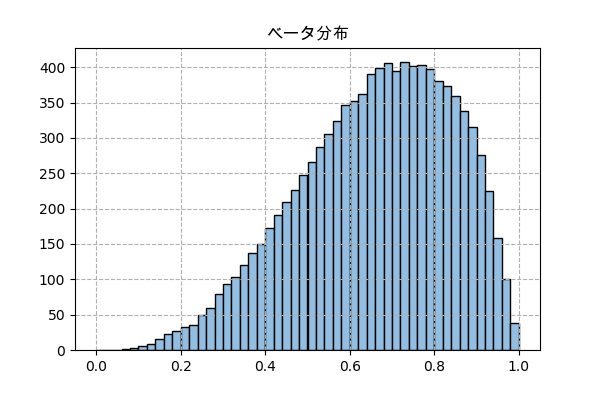
この分布を表現する方法は色々あるはずですが、ここでは0から1の確率の区間を50に分けて考慮します。
4回の中で3回成功するという場合を考えます。
n_sampl = 10000 # サンプリング回数
n_bin = 50 # 分ける区間の数
n = 4 # 全部の回数
k = 3 # 成功の回数
p = [] # 区間の番号を格納するリスト
x = (np.arange(n_bin)+0.5)/n_bin # 各区間の確率の中心 (0.01, 0.03, 0.05, ..., 0.99)
i_shikou = 0 # 試行した回数
while(i_shikou<n_sampl):
rand = np.random.random(n) # 成功か失敗かを決める数字をランダム
for i in range(n_bin):
# その区間の確率での場合で成功する回数
if((rand<=x[i]).sum()==k):
# 特定の数と同じなら区間の番号を格納
p.append(i)
i_shikou += 1
y = np.bincount(p)
plt.title('ベータ分布',family='Arial Unicode MS')
plt.bar(x,y,width=1/n_bin,color='#92bee1',ec='k')
plt.grid(ls='--')
plt.savefig('beta.png',dpi=100)
plt.close()
plt.histではなくnp.bincountとplt.barを使っているが、ベータ分布も連続型分布だから実際に描いたのはヒストグラム。
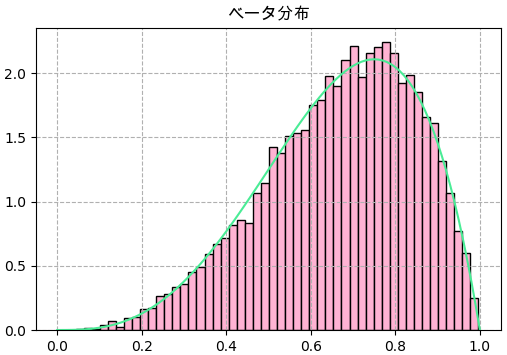
scipy.statsで実装
α = k+1 # 4
β = n-k+1 # 2
f = scipy.stats.beta(α,β)
plt.title('ベータ分布',family='Arial Unicode MS')
plt.hist(f.rvs(10000),50,color='#ffb3d3',ec='k',density=True)
x = np.linspace(0,1,101)
plt.plot(x,f.pdf(x),'#4aec96')
plt.grid(ls='--')
plt.savefig('beta2.png',dpi=100)
plt.close()
纏め
実際にランダムして結果を見ると、やはりこういう分布がこうやって起こるんだな、と実感できて理解を深めて納得できますね。
以上説明した分布をここで纏めています。
| 名 | 関数 | xの範囲 | scipy.stats | パラメータ |
|---|---|---|---|---|
| 二項分布 | $C(n,x)p^x(1-p)^{n-x}$ | 0,1,2,...,n | scipy.stats.binom(n,p) | $n\in${$1,2,3,...$}, $p\in[0,1]$ |
| ベルヌーイ分布 | $p^x(1-p)^{1-x}$ | 0,1 | scipy.stats.bernoulli(p) | $p\in[0,1]$ |
| 幾何分布 | $p(1-p)^{x-1}$ | 1,2,... | scipy.stats.geom(p) | $p\in[0,1]$ |
| 負の二項分布 | $C(x+r-1,x)(1-p)^rp^x$ | 0,1,2,... | scipy.stats.nbinom(r,p) | $r\in${$1,2,3,...$}, $p\in[0,1]$ |
| ポアソン分布 | $\frac{λ^x e^{-λ}}{x!}$ | 0,1,2,... | scipy.stats.poisson(λ) | $\lambda\in(0,\infty)$ |
| 連続一様分布 | $\frac{1}{b-a}$ | [a,b] | scipy.stats.uniform(a,b) | $a\in(-\infty,\infty)$, $b\in(-\infty,\infty)$ |
| 指数分布 | $λe^{-λx}$ | [0,∞) | scipy.stats.expon(0,λ) | $\lambda\in(0,\infty)$ |
| 正規分布 | $\frac{1}{\sqrt{2πσ^2}}e^{\left(-\frac{(x-μ)^2}{2σ^2}\right)}$ | (-∞,∞) | scipy.stats.norm(μ,σ) | $\mu\in(-\infty,\infty)$,$\sigma\in(0,\infty)$ |
| カイ二乗分布 | $\frac{x^{k/2-1}e^{-x/2}}{,2^{k/2} \Gamma(k/2)}$ | [0,∞) | scipy.stats.chi2(k) | $k\in${$1,2,3,...$} |
| ベータ分布 | $\frac{x^{α-1}(1-x)^{β-1}}{B(α,β)}$ | [0,1] | scipy.stats.beta(α,β) | $\alpha\in(0,\infty)$,$\beta\in(0,\infty)$ |
この記事にも参考に: