代表的な確率分布の特徴まとめ

この記事について

代表的な確率分布の使いどころや関係性について直感的に思い出せるように、特徴についてまとめます。

早見表

概要

名称	概要	再生性	形式	共役分布	備考
二項分布	複数回のコイントスで表がk回でる確率	〇	離散	ベータ分布	視聴率調査や、復元抽出時の不良品検査等で利用される
幾何分布	コイントスで初めて表(成功)がでるまでの試行数の確率		離散		無記憶性を持つ唯一の離散確率分布
超幾何分布	コイントスをした複数の人の何人かに表裏の結果を尋ねた時にk人が表である確率		離散		非復元抽出での不良品検査で利用される。
負の二項分布	コイントスで表(成功)がk回でるまでの試行数の確率	〇	離散		平均発生数が一定と仮定できない(ポアソン分布が適しない)計数推定に利用できる
多項分布	サイコロで各面の目がk1,k2,...k6回でる確率		離散	ディリクレ分布	結果が複数のカテゴリに分類される場合に適合する。k=2の時、二項分布となる。
ポアソン分布	電話が1時間にk回鳴る確率	〇	離散	ガンマ分布	稀に発生する現象に適合する
指数分布	次に電話が鳴るまでの時間の確率		連続		ポアソン分布で発生する現象の発生時間間隔は指数分布となる。また、無記憶性を持つ唯一の連続確率分布となる。
ガンマ分布	電話がk回鳴るまでの時間の確率	〇	連続		指数分布に従う確率変数X1,X2,..Xnの和
ワイブル分布	電話が故障するまでの時間の確率		連続		信頼性寿命予測に適用される
ベータ分布	偏りがあるかもしれないコインの表の出る確率を、コイントスの結果から推定した時の確率(確信度)		連続		一様分布はベータ分布の特別バージョン。
ディリクレ分布	偏りがあるかもしれないサイコロの各面が出る確率を、サイコロを振った結果から推定した時の確率(確信度)		連続		複数のカテゴリからなる事象の生起確率を表現できる。 文書分類等で応用される。
正規分布	テストの点数の分布	〇	連続	正規分布 or 逆ガンマ分布	自然現象や社会現象によくあてはまる。ブラウン運動で記述される事象は正規分布に従う。 母集団からサンプリングした標本の平均は正規分布に従う(中心極限定理)
対数正規分布	ある期間に電話が鳴る頻度の確率		連続		幾何ブラウン運動で記述される事象は対数正規分布に従う。 ワイブル分布が適さないケースでの信頼性解析に適用される。
χ2分布	コインやサイコロの出方に偏りがある確率	〇	連続		標準正規分布に従う確率変数の二乗和。仮説検定に使われる(χ2検定)

• コイントス

  • 成功か失敗かいずれかで表される事象
  • 各試行は独立

• サイコロ

  • K種類の状態で表される事象
  • 各試行は独立

• 電話

  • 離散的に発生する事象
  • 各事象の生起は独立

• テスト

  • 平均を最頻値とし、値が離れると発生率が下がる事象
  • 発生率の低減度合は離れる方向によらず一定
  • 各試行は独立

パラメータ

確率分布	母数	平均
二項分布	n:試行回数 p:成功率	$$np$$
幾何分布	p:成功率	$$\frac{1}{p}$$
超幾何分布	N:総数 k：成功状態数 n：抽出数	$$n\frac{K}{N}$$
負の二項分布	r:成功までの回数 p:成功率	$$\frac{pr}{1-p}$$
多項分布	n:試行回数 pk:各試行の発生確率	$$np_k$$
ポアソン分布	λ:平均発生数	$$\lambda$$
指数分布	λ:平均時間間隔	$$\frac{1}{\lambda}$$
ガンマ分布	k:形状母数 Θ:尺度母数	$$k\theta$$
ワイブル分布	η:尺度母数 m:形状母数	$$\eta\Gamma\biggl(1+\frac{1}{m}\biggl)$$
ベータ分布	α,β:形状母数	$$\frac{\beta}{\alpha+\beta}$$
ディリクレ分布	K:変量数 αk:集中度母数	$$\frac{\alpha_{i}}{\sum_{k}\alpha_{k}}$$
正規分布	μ:平均 σ:標準偏差	$$\mu$$
対数正規分布	μ:平均 σ:標準偏差	$$\mu$$
χ2分布	k:自由度	$$k$$

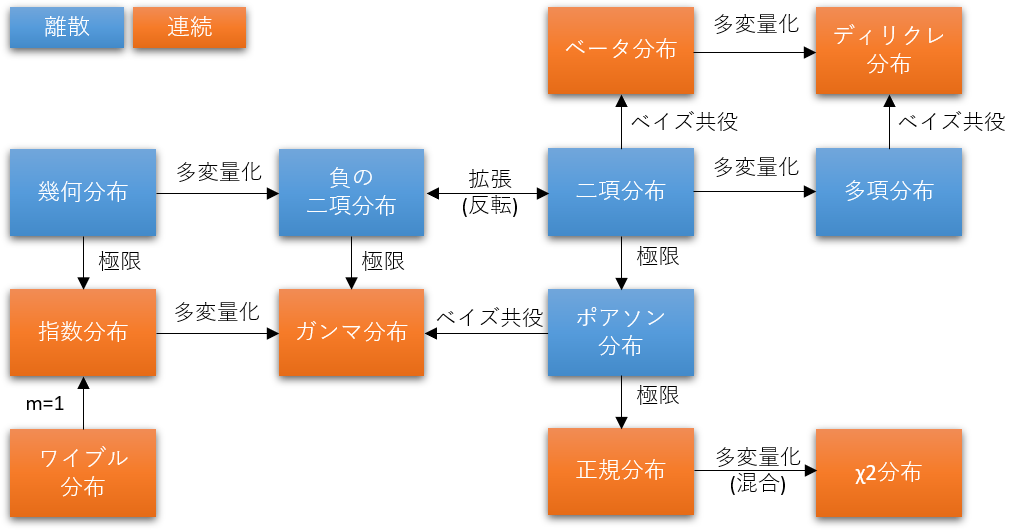
関係性

補足

超幾何分布

• 二項分布と対照的な関係となります
• どちらの分布も一定の試行回数中に起こる成否回数を表現します
• 二項分布と違って試行ごとに次の成否確率が変化します
• 母集団の数が非常に大きい場合、成否確率の変化が小さくなるため、二項分布を近似的に適用できます（非復元抽出でも二項分布を適用できる)

負の二項分布

• 負の二項分布はポアソン分布とガンマ分布の無限混合分布と考えることができます

p(X|φ,μ) = \int_{0}^{∞}Poisson(X|λ)Gamma(λ|φ,μ)dλ

• これは、平均λがガンマ分布に従って変動するポアソン分布と見るイメージです

• 条件によって発生数に変化のある突発的現象に当てはめることができます

  • e.g 交差点の交通事故発生数(昼夜、天候で発生数が異なる可能性があるため)

• マーケティング分野で消費者行動予測に応用されます

  • NBDモデル
    • r：購買回数
    • M: 平均購買回数
    • K: 形状パラメータ(Mの影響を受ける)
  • Kを拡大できるMの拡大方法の分析に利用できます
    • 例
      • 既存顧客に向けての販促によるMの向上
      • 新規顧客に向けての販促によるMの向上

P_r = \frac{(1+K/M)^{-K}\Gamma(K+r)}{\Gamma(r+1)\Gamma(K)}\biggl( \frac{M}{M+K} \biggl)^r

ポアソン分布

• 待ち行列理論で指数分布とともによく利用されます
  • M/M/1モデル
• カウントデータの時系列予測で応用されます（ポアソン回帰分析)

  • 例

    • ソフトウェア欠陥数の予測
    • Webコンバージョン数の予測

  • 回帰式

    • 定義
      • λ ：発生件数期待値
      • β0：定数
      • βk：偏回帰係数
      • ε ：回帰誤差
    • リンク関数を対数変換とした一般化線形モデルと考えることができます
    • 最尤法で係数を求めます(回帰誤差は正規分布ではありません)

ln(λ)=β{_0}+β{_1}X{_1}+β{_2}X{_2}+...++β{_k}X{_k}+ε

ガンマ分布

• 形状母数kを正に固定することで、トラフィック理論の呼到着やサービス時間の表現に使われる**アーラン分布**となります

ディリクレ分布

• 自然言語処理におけるトピックモデル(各トピックに各種単語が所属する確率)の算出で利用されます(LDA：Latent Dirichlet Allocation/潜在ディリクレ過程)
  • 尤度：多項分布
  • 事前分布：ディリクレ分布

ワイブル分布

• さまざまな製品の信頼性データの解析に広く適用されています

  • 故障モード(要因)で形状パラメータを変更します
    • 初期故障
      • 製造工程の遺物混入等が原因の故障
      • 形状パラメータm<1に設定されます
    • 偶発故障
      • 初期故障要因を除去しても残存する原因による故障
      • 形状パラメータm≒1に設定されます
    • 摩耗故障
      • 耐用寿命による摩耗故障
      • 形状パラメータm>1に設定されます
  • 故障率を測定した時にmかηのどちらに変化があるか分析します
    • ηの変化の場合、故障までの時間が変化したと解釈できます
    • mの変化の場合、故障モードの変化のため、物理的な故障要因が変化したと解釈できます
  • 例
    • 製品寿命変化の要因分析
    • モーターの摩耗故障を防ぐための定期保守のタイミング

• 化学反応や半導体故障が原因の製品劣化過程には適さない場合があります

  • この場合、対数正規分布でモデル化する場合があります

• 形状パラメータが2の時、**レイリー分布**となります

  • 通信工学における電波減衰等の解析に使われます

χ2分布

• χ2検定として以下のような統計的有意性の検証に利用されます
  • サンプリングしたデータが理論確率分布に適合するか
    • 例：カウントデータがポアソン分布に適合しているか
  • サンプリングしたデータのカテゴリ変数間が独立か
    • 例：発生したソフトウェア不具合の混入パターンが、出勤曜日に関係しているか

共役事前分布

ある事象Xについて推定したいとき、その事象Xが発生する確率分布P(X)を適当に仮定し、あるデータを観測した後、その取得したデータの発生確率を使って、最初に仮定した事象Xの発生する確率分布を更新する推定方法をベイズ推定と呼びます。

ベイズ推定では、最初に仮定するの事象Xの発生する確率分布を事前確率分布P(X)、データDに基づいて更新する確率分布を**事後確率分布P(X|D)が登場します。更新を繰り返すことで、この事後確率分布の確度をあげていきます。この更新を行う係数として尤度P(D|X)**を使います。これは、事象Xが発生した際にデータDが取得できる確率分布を表しています。ベイズの定理より、以下の式で更新を行います。

P(X|D) \propto P(D|X)P(X)

ベイズ推定では、データが取得できる確率分布(尤度)を適当に仮定します。その上で、母数の事前分布を過去の経験より定めると、上式で事後分布を更新していくことができます。

この時、事前確率分布と事後確率分布が尤度を掛け算した前後で同じ分布であると、とても都合がよくなります。このような確率分布を尤度に対する共役事前分布といいます。