前回の続きです。
他のクラスタリング手法との比較
距離ベースのクラスタリング手法であるk-meansと密度ベースのクラスタリング手法であるDBSCANと比較してみます。
k-meansについてはこちらのページで少し解説しています。簡単に言うと、各データ点を最も近いクラスタに所属させて新しいクラスタ重心を計算するということを繰り返してクラスタを構築していきます。
DBSCANは指定した密度以上のデータ点集合を探して、それらをニョキニョキ成長させることでクラスタを構築する手法です。
k-meansの場合は距離ベースなので二次元データでは円形、三次元データでは球形のクラスタ構築しか出来ないことがわかっています。DBSCANは密度ベースなのでk-meansよりもより複雑な形状に対応することが可能です。
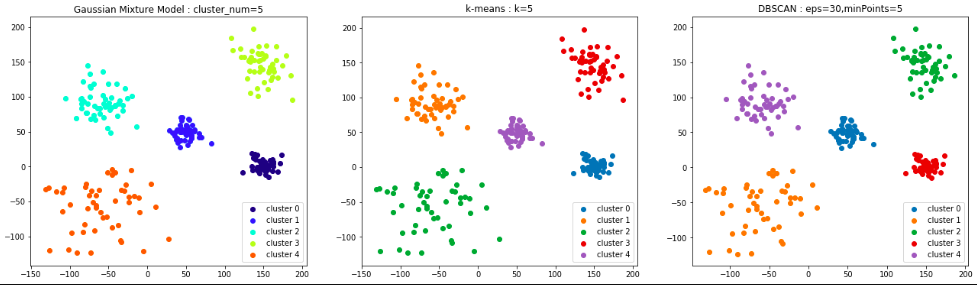
以下は実際に前回のデータを使って各手法でクラスタリングした結果です。
混合ガウスモデル、k-means、DBSCANの順番で図示しています。
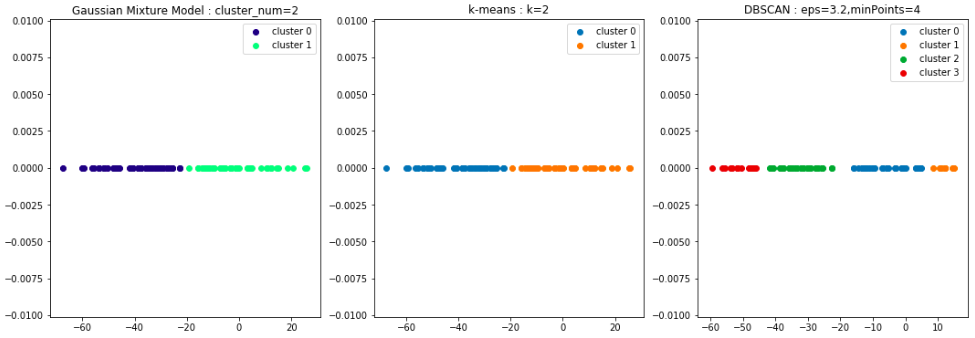
一次元データ
混合ガウスモデルとk-meansはほぼ同じ結果になっています。
DBSCANについてはなんとかそれっぽくなるようなパラメータを探しましたがこのくらいが限度でした。ただ、本来のクラスタ数を知らない前提ならきれいにクラスタが構築されていると思います。
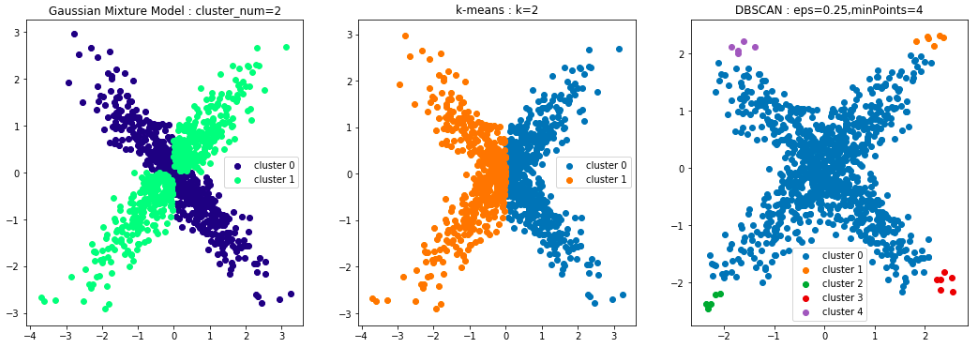
次はX!
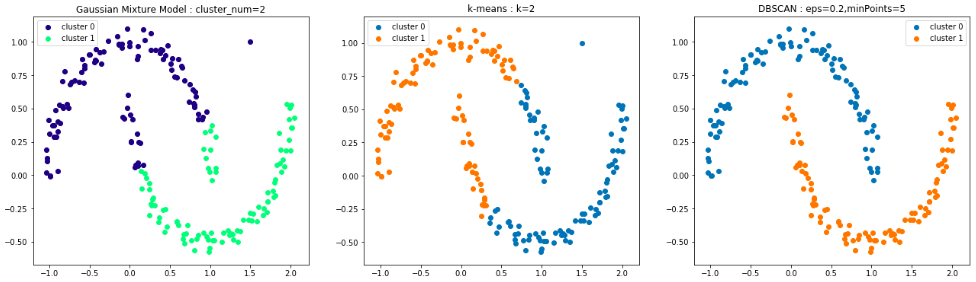
各手法の特徴が良くでています。
このデータは2本の線をクロスさせたような形になっており、それぞれの線はガウス分布に従って生成したような感じです。
よって、混合ガウスモデルでは、どちらかの線を選択して一つのクラスタとしており、もう片方の線は途中で分断されていますが一つのクラスタとしています。
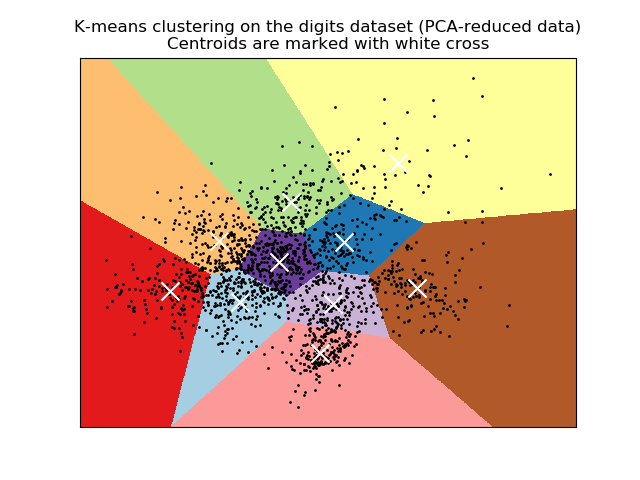
k-meansは距離ベースのクラスタリング手法であり、今回のようなデータは分離できません。下図の公式の例にもあるように、k-meansによって構築したクラスタをエリア別に図示すると以下のようになり、クラスタエリアの境界は直線になります。今回の例でもきれいに直線になっていますね。
DBSCANについてはなんとかXの中心部分を一つのクラスタにするようにパラメータ設定してみました。密度ベースなので、密度の高い部分をクラスタとして構築していきます。(全データが表示されていませんが、表示されていないデータ点はどのクラスタにも含まれなかったことを表しています。)
密度の異なるデータ
今回は混合ガウスモデルとDBSCANが同じような結果となり、k-meansはさきほどのデータと同じように直線でクラスタ境界が引かれています。
ただし、DBSCANは与えられたデータに存在する各クラスタの密度がある程度同じことを前提としているので上手に分割するためのパラメータ選択はかなりシビアです。
一方、混合ガウスモデルは各クラスタに対応するガウス分布の分散のパラメータによってその密度を変更することが出来ます。
つまり、各クラスタの密度が異なることが想定されるデータに対しては混合ガウスモデルを使ったほうが良さそうです。
きれいなデータ
このデータはどれも同じような結果にすることができました。ただし、DBSCANのパラメータ選択はやはり少し難しいです。探索半径を表すパラメータepsのスケールがデータによって違いすぎるので、データを正規化したあとに適用したほうが良さそうです。(普通そうするのかもしれませんがどなたか教えてください。。。)
混合ガウスモデルできれいにクラスタ構築できないデータ
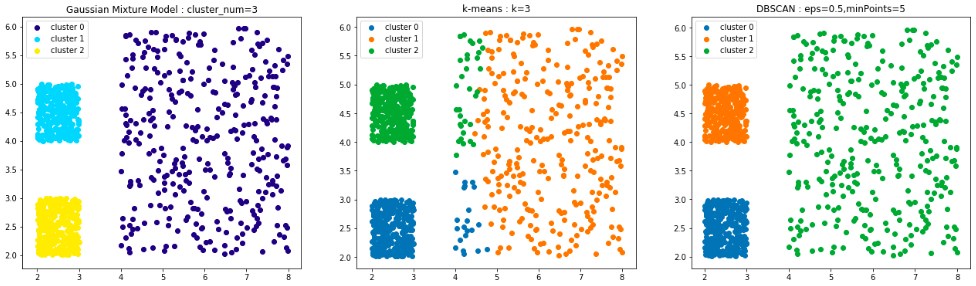
最後はこれです。
このデータではDBSCANのみ正しくクラスタ構築できています。
DBSCANは密度ベースのクラスタリング手法なので、同じような密度でニョキッと伸びているようなクラスタはパラメータさえきちんと設定すれば見つけてくれます。
k-meansは二次元上では円形にデータを探索していくのでこのデータを分離することはできません。
混合ガウスモデルはそもそもガウス分布に従って生成されたデータがあることを前提としており、このデータのような形の場合は見つけることができません。(前回にも書いたとおり、二次元上ではガウス分布に従うデータは中心が濃い円形のような形になります)
(追記)
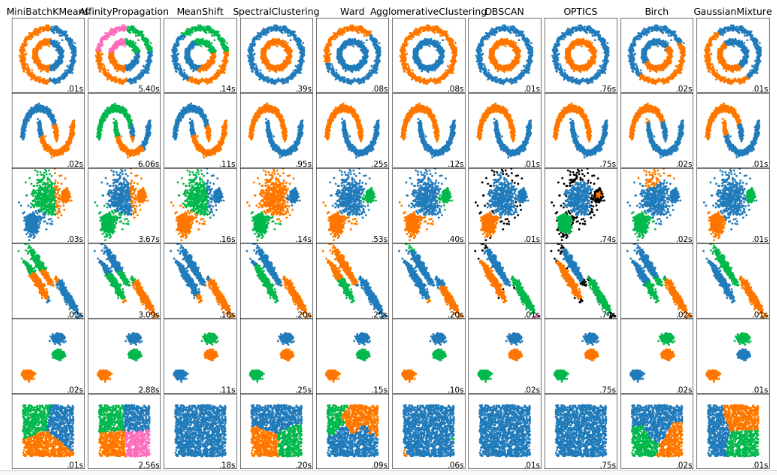
公式に色んなデータを色んな手法でクラスタリングした結果が載っていました。
ドキュメントすごく充実してる感じなので参考にしていきたいです。
その3に続く
その3では混合ガウスモデルで最適なクラスタ数を選ぶための指標AICやBICについてやEMアルゴリズムについて書く予定です!(予定)