最近クラスタリングについて調査している中で出会った、混合ガウスモデル(Gaussian Mixture Model, GMM)について調査した内容です。
※私の現時点での理解を書いているので間違っている箇所もあるかもしれません。その場合は指摘していただけると喜びます。
混合ガウスモデルの特徴
- クラスタリングの手法の一つ
- あるクラスタに属するデータ群がガウス分布に従っていると仮定する
ガウス分布とは
ガウス分布とは正規分布の別名です。
正規分布は平均$\mu$と分散$\sigma$のパラメータを指定することでその形状を決定することが出来る確率分布です。
その形状は以下のように左右対称の山のような形をしています。
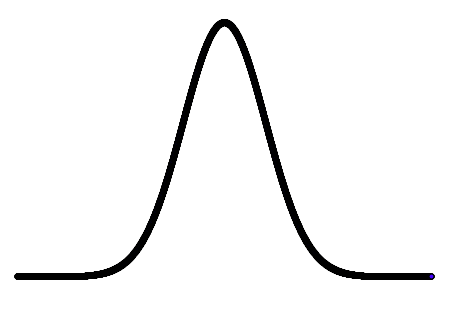
山の頂上部分が平均$\mu$、山の幅が$\sigma$に対応しています。
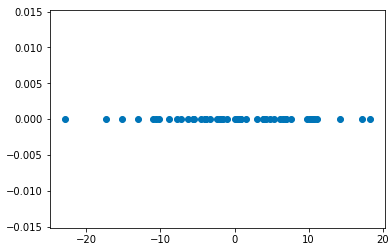
以下のようにすれば、pythonを使ってガウス分布(正規分布)に従ったランダムなデータを生成することが可能です。
# ガウス分布に従うランダムなデータを生成
import numpy.random as rnd
data = rnd.normal(0,10,50)
# 結果を散布図で可視化
import matplotlib.pyplot as plt
plt.scatter(data,[0 for i in range(50)])
rnd.normal(mu,sigma,array_size)は第一引数に平均$\mu$、第二引数に分散$\sigma$、第三引数に出力データサイズを指定します。
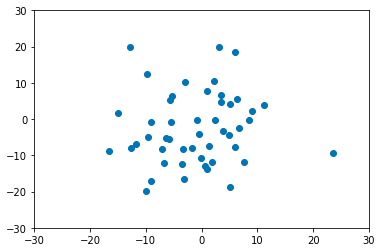
二次元ならこんな感じです。
# ガウス分布に従うランダムなデータを生成
import numpy.random as rnd
data = rnd.normal(0,10,(50,2))
# 結果を散布図で可視化
import matplotlib.pyplot as plt
plt.scatter(data[:,0],data[:,1])
plt.xlim(-30,30)
plt.ylim(-30,30)
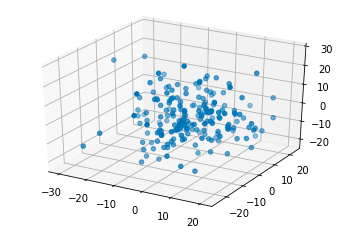
三次元ならこんな感じ。参考URL
from mpl_toolkits.mplot3d import Axes3D
import numpy.random as rnd
data = rnd.normal(0,10,(200,3))
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(data[:,0],data[:,1],data[:,2])
イメージ的には一次元だと山、二次元は円、三次元は球という感じだと思います。(いずれも中心が濃い)
四次元以上は可視化できませんが、同じようにイメージしていればよいはずです(なかなかイメージ出来ませんが。。。)
混合ガウスモデル
混合ガウスモデルでは、与えられたデータはいくつかのクラスタから構築されているはずであり、それぞれのクラスタはガウス分布に基づいて生成されているだろうと仮定します。
この仮定のもと、それぞれのクラスタがどんなガウス分布で表せるかを推定する手法です。
上述したように、ガウス分布(正規分布)はその平均$\mu$と分散$\sigma$を決定すればその形が決まるので、内部的にはこれらのパラメータを推定します。
やってみる
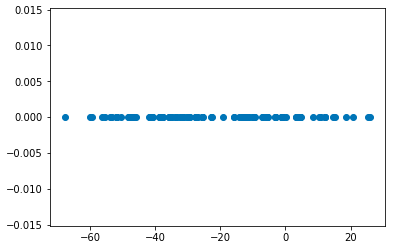
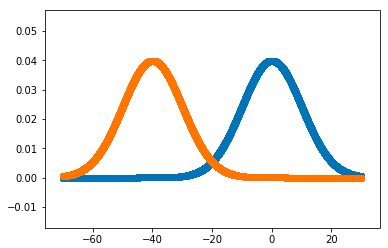
このデータは以下のように2つの異なるガウス分布に従って生成したデータです。
import numpy.random as rnd
data1 = rnd.normal(0,10,50) # 平均0、分散10
data2 = rnd.normal(-40,10,50) # 平均-40、分散10
data_all = np.append(data1,data2)
plt.scatter(data_all,[0 for i in range(100)])
山で可視化すると以下のような感じです。
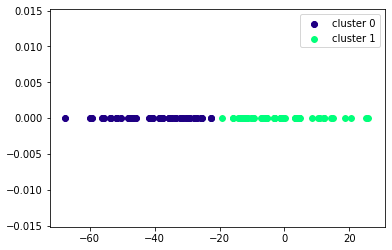
実際に上記のデータをscikit-learnの混合ガウスモデルの実装であるGaussianMixutureクラスで解いてみました。
# 混合ガウスモデルでクラスタリングと可視化
from sklearn.mixture import GaussianMixture
from matplotlib import cm
# 想定するクラスタ数
cluster_num = 2
# データのshapeをあわせる(もっとうまいことできるはず。。。)
data_all = data_all.reshape((100,1))
data_all_2d = np.concatenate([data_all,np.zeros((100,1))],axis=1)
data_all_2d = data_all_2d.reshape((100,2))
# 各クラスタ用のガウス分布のパラメータを推定してデータをクラスタリング
pred = GaussianMixture(n_components=cluster_num).fit_predict(data_all_2d)
# 可視化
for i in range(cluster_num):
cluster_datas = data_all_2d[pred==i]
color = cm.jet(i/cluster_num)
plt.scatter(cluster_datas[:,0],cluster_datas[:,1],c=color,label='cluster {}'.format(i))
plt.legend()
plt.plot()
たしかにそれらしく2つのクラスタに分けることが出来ています。
いろんなデータでやってみた
(二次元データ)
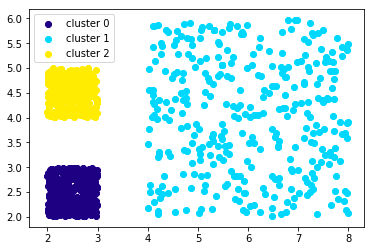
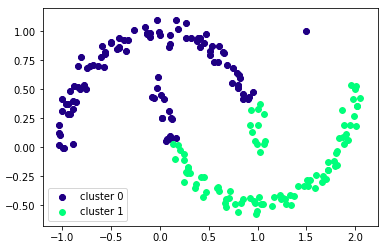
以下はうまくクラスタリング出来ている例です。
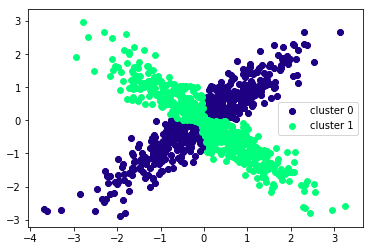
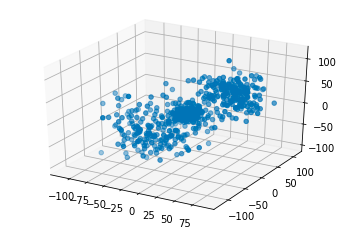
混合ガウスモデルの定義から自明ですが、ガウス分布に従っていない上のようなデータは正しくクラスタリングすることができません。
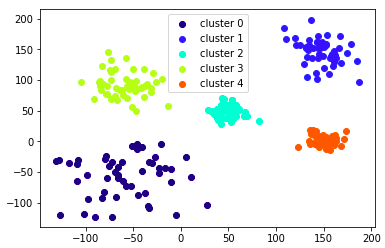
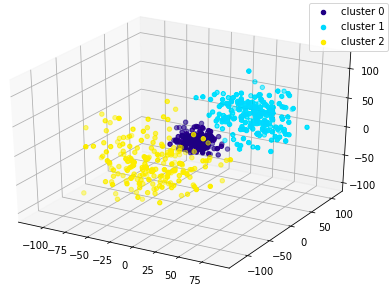
これもぱっと見はわかりませんが、ガウス分布に従って3つのデータを生成しているのでそれなりに正しくクラスタリングできています。
長くなりそうなのでその2に続きます