代表的な非階層型クラスタリング手法としてk-meansが知られています。
k-meansは構築するクラスタ数kを入力として与える必要がありますが、最適なkの値は試行錯誤しながら探す必要があります。
このkを自動推定するための手法としてエルボー法という手法があります。
k-means法とは
与えられたデータをk個のクラスタに分割する比階層的クラスタリング手法です。
k-meansの動作イメージは以下のページがものすごくわかりやすいです。
K-means 法を D3.js でビジュアライズしてみた
k-meansのイメージは↑のような感じですが、数学的には以下の式を最小化する問題として定式化することができます。
\sum_{i=1}^{k}\sum_{p\in C_{i}}(p-c_{i})^2
ここで、$k$はクラスタ数、$C_{i}$は$i$番目のクラスタに含まれるデータ点集合、$c_{i}$は$C_{i}$の重心です。
また、この値はSSE(Sum of Squared errors of prediction)と呼ばれます。
エルボー法とは
エルボー法では、クラスタ数を変えながら上記のSSEを計算し、結果を図示することで最適(と思われる)クラスタ数を推定する手法です。
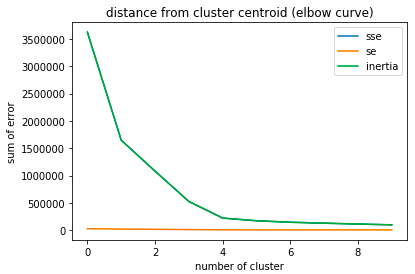
クラスタ数を変えながらSSEを計算し図示することで、例えば以下のようなグラフになります。
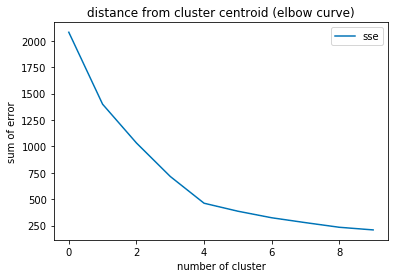
横軸にクラスタ数、縦軸にSSEを図示すると、肘(エルボー)のようにポキっと曲がった場所があることがわかります。
上記の例ではクラスタ数=4の点でグラフがポキっと曲がっていますね。
エルボー法ではこのような点を見つけることで最適な(と思われる)クラスタ数を推定します。
sklearn.cluster.KMeans
scikit-learnのk-means用のクラスを調べると、以下のような記述があります。
Attributes:
inertia_ : float
Sum of squared distances of samples to their closest cluster center.
そうです。
この値を使えば一発でSSEにアクセスできます。
ソースコード
全文はここに置いています(jupyter notebook)。
今回は私の理解のために、上記のinertia_を使って算出したSSEを別の方法でも算出して間違いがないか確認しました。
実際にエルボー法でSSEを計算しているのは以下の部分です。
# エルボー法で最適なクラスタ数を探索する
sse = np.zeros((max_cluster_num,)) # Sum of Square Error(クラスタ内誤差平方和)
se = np.zeros((max_cluster_num,)) # Sum of Error(クラスタ内誤差和)
inertia = np.zeros((max_cluster_num,)) # scikit-learnにより自動計算するクラスタ内誤差平方和
for i in range(max_cluster_num):
cluster_num = i + 1
kmeans = KMeans(n_clusters=cluster_num)
# 各データがどのクラスタに所属するか
pred = kmeans.fit_predict(data_array)
inertia[i] = kmeans.inertia_
# 各データが自身の所属するクラスタ中心からどれだけ離れているか調べる
transforms = kmeans.transform(data_array)
distances = np.zeros((data_array.shape[0]))
for index in range(len(transforms)):
distances[index] = transforms[index,pred[index]]
se[i] = np.sum(distances)
sse[i] = np.sum(distances**2)
結果
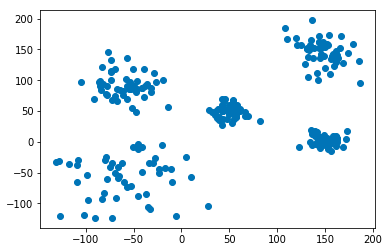
今回使用したデータは以下の2次元データです。
正規分布で適当なパラメータを指定して5クラスタになるようにしました。
クラスタ4のあたりでポキっと折れてますね。
今回の場合は実際にはクラスタ数5が正解なのですが、分析するデータが2次元(もしくは3次元)で可視化可能なことは稀だと思います。
データがどういう形をしているのかわからないという前提で考えればクラスタ数4という推定はまぁまぁ良い結果では無いでしょうか。
最適だろうと推定したクラスタ数プラマイ1ずつ(3、4、5)の結果を図示してみました。
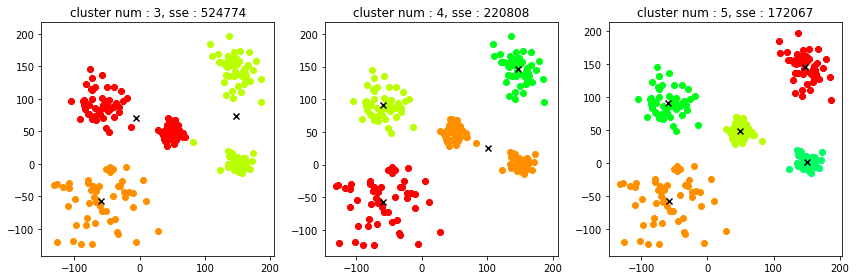
並べてみるとクラスタ数5が最適なことは明確ですが、クラスタ数3の結果とクラスタ数4の結果を比べるとなんとなく今回の結果になったことも納得できる気がします。
間違いなどあったらぜひご指摘ください。