オミータです。ツイッターで人工知能のことや他媒体で書いている記事など を紹介していますので、人工知能のことをもっと知りたい方などは @omiita_atiimoをご覧ください！
他にも次のような記事を書いていますので興味があればぜひ！

GANへの新しい正則化「ICR」が期待大な件&解説

本記事ではICLR2020に登場した[Zhang, H.(ICLR'20)]とその改良版となる[Zhao, Z.(2020)]についてまとめて解説します(改良版を中心的に解説します)。過去記事GANにもオーギュメンテーションは超有効だった！DAだけでSoTA達成した最新論文を解説！で簡単には触れましたが、今回はGANへの新たな正則化手法「Consistency Regularization」(以下、CR)とそれを改善させた「Improved Consistency Regularization」(以下、ICR)について詳しく迫っていきます。CRは半教師あり学習などですでに使われ大きな成果を出していますが、今回紹介する論文ではCRをGANにも適用させ性能をがっつり上げています。後続のICR(のうちbCR単体)は私自身実際に使用してその効果をしっかりと確認できたので、すごくおすすめです。実装もとても簡単です。そのため、この先Spectral Normalizationのように標準的に使われてもおかしくないと思っています。それでは早速CR/ICRの仕組みとその凄さを見ていきましょう！

本記事の流れ:

忙しい方へ
ICRの説明
- Data Augmentation
- Consistency Regularization
- Improved Consistency Regularization
  - balanced CR (bCR)
  - latent CR (zCR)
CR/ICRの実験結果
まとめと所感
参考

略称	名称
DA	Data Augmentation
G	Generator
D	Discriminator
CR	Consistency Regularization
bCR	balanced Consistency Regularization
zCR	latent Consistency Regularization
ICR	Improved Consistency Regularization
SN	Spectral Normalization
FID	Fréchet Inception Distance
IS	Inception Score

(略称多すぎですね。)

0. 忙しい方へ

GANにConsistency Regularizationを適用することで性能を大きく改善したよ
Improved-CRは「balanced-CR + latent-CR」だよ
- bCRはリアル画像とフェイク画像両方にCRしたものだよ
- zCRはノイズ空間のCRをしたものだよ
CRもICRも超絶シンプルで強力だよ
CRとICRはSNとの相性が良く、他の正則化手法を大きく上回ったよ
ICRはCIFAR-10(FID:9.21)とImageNet(FID:5.38)でBigGANにおけるSoTAを達成したよ

1. ICRの説明

ICRはとてもシンプルな手法です。ICRの説明のためにここでは以下のように順を追って説明していきます。

Data Augmentation(=DA)
Consistency Regularization(=CR)
Improved CR(=ICR) 3.1 balanced CR(=bCR) 3.2 latent CR(=zCR)

1.1 Data Augmentation

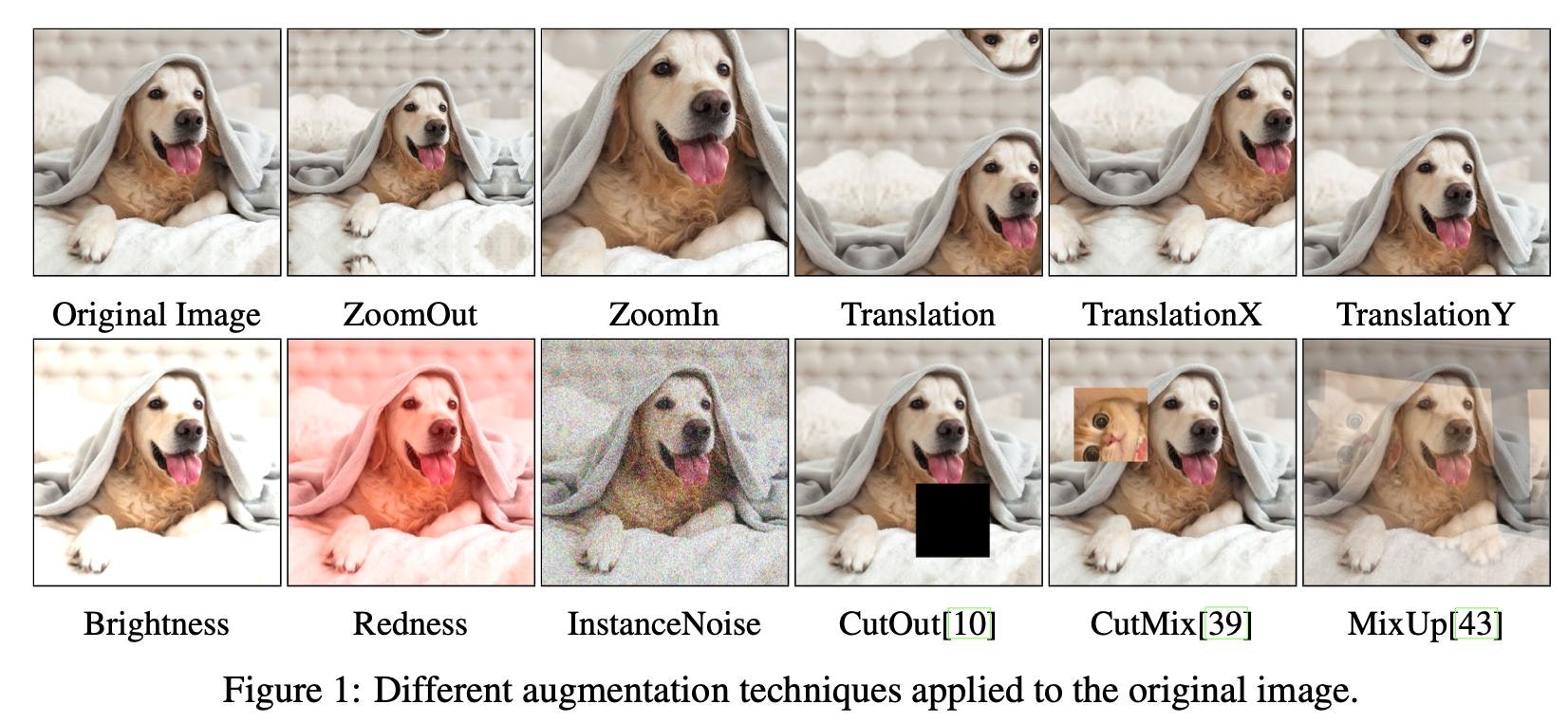
画像認識モデルを少しでも触ったことのある方なら既知だとは思いますが、CRにとってData Augmentation(以下、DA)について説明いたします。ここでのDAはわかりやすさのため画像に対するDAを指します。上図はその例をいくつか表していますが、DAとは「画像本来の意味を大きく変えない処理を画像に加えることでデータ数を水増しする技術」です。「画像本来の意味」というのはつまり画像ラベルのことですね。そのラベルが大きく変わらない程度の処理ということなので、例えば左右反転が画像認識ではよく使われています。犬の画像は左右反転させても犬のままなので合点がいきます(†)。DAは学習データが大量にあればあるほど良いとされるディープラーニングととても相性がよく、性能向上には今や欠かせない存在となっています。DAに関してもう少し詳しく知りたい方は様々なDAをまとめた拙著記事(シリーズもの)をご覧ください。

このようにDAは「本来の意味を変えない処理」という前提のもとで成り立っていますが、続いて紹介するConsistency RegularizationはDAのこの前提ををうまく利用したものになっています。

(†) ちなみに文字画像に対して水平反転を適用するのはDAとして少し危険な可能性があります。小文字の「b」を左右反転すると「d」となってしまうなど本来の意味が保存されないケースが出てしまう可能性があるからです。

1.2 Consistency Regularization

ここで紹介するCR-GANはICLR2020での[Zhang, H.(ICLR'20)]にて提案された手法です(†)。CRとはとてもシンプルで、単にDiscriminatorの損失関数にConsistency正則化項を追加したものとなっています。「いやConsistency正則化ってなんだよ」となってしまうのでもう少し詳しく説明します。

そもそもConsistencyとは日本語で「一貫性」と訳されます。なのでConsistency正則化とは、何かしらの一貫性をDiscriminatorに強制させるもの、と捉えることができます。ではなんの一貫性を強制させるか、ということですがここで登場してくるのがDAです。先ほど説明したように、DAとは「本来の意味を変えない処理」なのでDA適用前と適用後ではその意味は一貫しているはずです。そして、CRとはDAのこの一貫性をDiscriminatorに叩き込むものなのです。GANのDiscriminatorにおける「本来の意味」とは画像の真偽のことなので、つまり、画像がDAされていてもその画像が真なのか偽なのかは一貫されているべき、ということを強制しています。

それではCRを用いたGANであるCR-GANについて数式で考えてみます。数式と言っても、難しいものではなくむしろ数式で考えた方が理解が早いと思います。DAはリアルな画像にしか適用しません。本物の画像データを$x$、 DAの処理を$T(\cdot)$とするとDA適用後の画像データは$T(x)$と表せ、Discriminatorを$D(\cdot)$とします。論文中では少し記号の定義揺れがあり、CRにおける$D(\cdot)$はDiscriminatorの最終層の活性化関数を適用する前の値となっています。そのため、CRを計算する箇所では$D(\cdot)$は最終層の活性化関数直前の値を表していることに注意してください。話を戻すと、CRは次の式を強制することになります。

$$
D(x) = D(T(x))
$$

これは単純に両辺の差分のL2ノルムをゼロにさせるようにDに仕向けることで達成できそうなので、CR項は

$$
L_{\mathrm{real}}=||D(x) - D(T(x))||^2
$$

と表せられます。リアル画像に対してCRを行っているので$L_{\mathrm{real}}$としました。最終的なDの損失関数はこのCR項を追加するだけなので、

$$
L_D^{cr} = L_{\mathrm{D}}+\lambda{L_{\mathrm{real}}}
$$

となります(††)。$L_{\mathrm{D}}$はNon-Saturating損失やHinge損失、Wasserstein距離など通常のDの損失関数です。Gは全くいじらないのでGに対する最終的な損失関数も$L_G^{cr}=L_G$です。CRはとても単純であるにもかかわらず大きなゲインをもたらしてくれます。ここで重要なのが、CRにおいてはDAはリアル画像のみに適用するということです。それではこのCRをさらに改良したICRの説明へと移りましょう。

(†) CR自体は新たな発想ではなく、半教師あり学習などでは強力な手法として広く用いられています[Sajjadi, M.(NIPS'16)]、[Berthelot, D.(NeurIPS'19)]。

(††) CR項の係数である$\lambda$は[Zhang, H.(ICLR'20)]の実験から $\lambda=10$をベストプラクティスとしています。また、CR項の$\mathrm{D}(\cdot)$はDの最終層の活性化関数を適用する直前の値で十分であると実験から結論づけています。

1.3 Improved Consistency Regularization (ICR)

ICRは[Zhao, Z.(2020)](†)において提案された手法で、「blanced CR」と「latent CR」という2つの手法を組み合わせたものとなっています。2つの手法を組み合わせたといってもいずれも先ほどのCRを理解していればとても単純なものなので簡単に理解ができると思います。

1.3.1 balanced CR (bCR)

CRではDAはリアル画像にのみ適用されました。これによって性能向上はしたもののCRは実はある問題を孕んでいたのです。それは 「GがDA適用後の画像も生成するようになってしまう」 という問題です。具体的には下図の右列のような画像を生成するようになってしまうのです。ここではCIFAR-10の画像に対してCutout[DeVries, T.(2017)]というDAを適用しています。Cutoutとは単に画像の一部をマスクする手法です。左列の(a)、(d)、(g)がCutoutを各マスクサイズで適用した真画像で、右列の(b)、(e)、(h)はGによる生成画像です。右列にCutoutされた画像も生成されてしまっていることがわかります。(c,f,iはbCRを用いた場合の結果を示しているのでここでは意図的に除いています。)

なぜこのようなことが起きてしまうのでしょうか。これは、CRではDAがリアル画像のみにしか適用されないことに起因しています。どういうことかというと、逆を言えばDAされていればリアル画像ということになるので、Gが「DAもリアル画像の特徴なんだな！」と勘違いを起こしてしまうということです。そのため、上図のCutoutのようなリアル画像にはない人工物(Cutoutで言うと黒マスク)を画像に含ませるようなDAをリアル画像にのみ適用してしまうと、Gがその人工物を生成するようになってしまうのです。この問題をどうにかしないとMixupやCutMixなどのより発展的なDAをCR-GANに対して使えないという事態が生まれてきてしまうというわけです。

この人工物生成問題を解決したものがbalanced CRになります。CRではリアル画像にのみDAをしていたのが原因であることを考えると、単にリアル画像とフェイク画像両方ともにDAをしてCRを行えば良さそうです。このリアル/フェイクいずれの画像でもCRを行ったものこそがbCRです。すごく単純ですね。このbCRは単純な改良ではありますが、とても強力です。私自身bCRを使ってみてその強力さを感じたのでイチオシです。Dの損失関数は、フェイクのCRである、

$$
L_{\mathrm{fake}}=||D(G(z)) - D(T(G(z)))||^2
$$

も加えるだけなので、

$$
L_D^{bcr} = L_{\mathrm{D}}+\lambda_\mathrm{real}{L_{\mathrm{real}}}+\lambda_\mathrm{fake}{L_{\mathrm{fake}}}
$$

となります。繰り返しになりますが、CRを計算する箇所では$D(\cdot)$は最終層の活性化関数直前の値を表していることに注意してください。$\lambda$はいずれもハイパーパラメータ(††)となります。依然としてGの損失関数は全くいじりません。そしてbCRを用いた場合の人工物の有無を見ると、見事になくなっています(左:真画像, 中央:CRによる生成画像, 右:bCRによる生成画像)。

最後にbCRの全体のアルゴリズムを示して次のzCRに移ります。(下のアルゴリズムでは損失関数にWassersteinを用いていますね。)

1.3.2 latent CR (zCR)

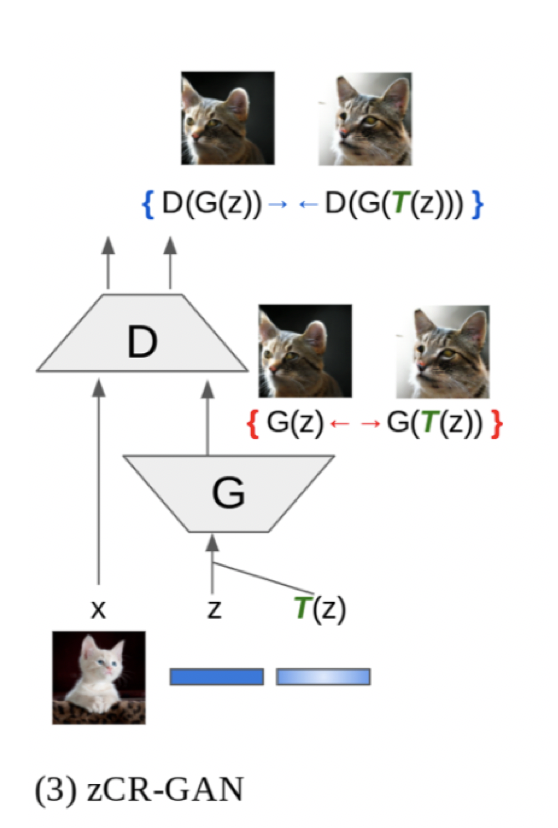
bCRだけでもCRを改善できているのですが、論文著者はさらにzCRも新たに提案しています。CRやbCRでは画像空間での一貫性を強制しましたが、zCRではノイズ空間での一貫性を強制しています。潜在空間への一貫性を行なうからlatent CRなのですが、これの略称を入力ノイズに一般的に使われる文字であるzを冠したzCRとしているのがオシャレに感じます。（latentをzと略すのは広く使われているものなのですかね。他の例があればコメント欄かTwitterで教えてもらえるとありがたいです。)

ノイズ空間への一貫性というのはつまり、ノイズ$z$にちょっとした変化を加えたとしてもDの出力は一貫しているべきという仮定を組み込んでいるということです。ここでのちょっとした変化というのはノイズ$z$に例えばさらに小さなガウシアンノイズ$\Delta z\sim\mathcal{N}(0,\sigma_\mathrm{noise})$を加えるといったものです。あとはこれでDの一貫性をとるために、

$$
L_{\mathrm{dis}}=||D(G(z)) - D(G(T(z)))||^2
$$

をDの損失関数に加えるだけです。なので、zCRにおけるDの損失関数は次のようになります。

$$
L_D^{zcr} = L_{\mathrm{D}}+\lambda_\mathrm{dis}{L_{\mathrm{dis}}}
$$

単純ですね。ただ実はこのままでは1つ問題が起きてしまいます。勘の良い方はすでに気付いてるかもしれませんが、この一貫性を達成させるためにGが望まない行動を取ってしまう可能性があります。それは、「どんなzが来ても全部同じ画像を生成する」というものです。つまり、モード崩壊を起こしてしまいます。これを阻止しGに多様性を持たせるために、Gの損失関数に次のような項を追加します。

$$
L_{\mathrm{gen}}=-||G(z) - G(T(z))||^2
$$

これは、ノイズ$z$と$T(z)$がGに入ったときに生成される画像同士の差分の負となっているので、これを最小にするということは差分の部分をものすごく大きくするということになります。よって、$L_\mathrm{gen}$を最小にすることで$G(z)$と$G(T(z))$が異なるものになってくれることが分かりますね。Gの損失関数を示すと、

$$
L_G^{zcr} = L_{\mathrm{G}}+\lambda_\mathrm{gen}{L_{\mathrm{gen}}}
$$

これでzCRは完成です(†††)。そして、bCRとzCRを同時に使うものをICRと呼んでいます。最後にzCRのアルゴリズムを下に示します。ここでも損失関数はWassersteinになっていますね。

(†) 論文著者の中には前述のCRの第一著者Zhang, H.氏も名を連ねています。この方はSAGAN[Zhang, H.(ICML'19)]の第一著者でもあります。

(††) bCRの具体的なハイパーパラメータの値は、$\lambda_\mathrm{real}=\lambda_\mathrm{fake}=10$などが使われています。

(†††) zCRの具体的なハイパーパラメータの値は、$\sigma_\mathrm{noise}=0.03$, $\lambda_\mathrm{dis}=5$, $\lambda_\mathrm{gen}=0.5$などが使われています。

2. ICRの実験結果

2.1 実験条件

データセット
- CIFAR-10
- CelebA-HQ-128
- ImageNet-2012-128
モデル
- SNDCGAN
- ResNet-SNDCGAN
- BigGAN
評価方法:
- Fréchet Inception Distance(FID)
- Inception Score(IS)
オーギュメンテーション:
- bCRでは水平反転 + ランダムクロップ
- zCRではガウシアンノイズ注入

実験は大きく分けて以下の3つです。
* 条件なし画像生成: ラベル情報を使わない画像生成
* 条件付き画像生成: ラベル情報を使う画像生成
* アブレーションスタディ

2.2 条件なし画像生成

条件なし画像生成においては、データセットにCIFAR-10とCelebA、モデルにSNDCGANとResNet-SNDCGANを用いています。比較手法として、他の正則化手法たちと比べています。:

略称	名称	論文
W/O	Withoutの略称(英語圏ではよく使われます)。正則化なし。	-
GP	Gradient Penalty	[Gulrani, I.(NIPS'17)]
DR	DRAGAN	[Kodali, N.(2017)]
JSR	Jensen-Shannon Regularizer	[Roth, K.(NIPS'17)]
CR	Consistency Regularization	[Zhang, H.(ICLR'20)](ICRの前身)
bCR	balanced Consistency Regularization	[Zhao, Z.(2020)](提案手法)
zCR	latent Consistency Regularization	[Zhao, Z.(2020)](提案手法)
ICR	Improved Consistency Regularization	[Zhao, Z.(2020)](提案手法)

損失関数はICRの前身である[Zhang, H.(ICLR'20)]においてそれぞれのデータセットやモデルの組み合わせで最も良かったものを使っています。また、ICRによる結果は2.2.4にまとめています。

2.2.1 CIFAR-10におけるSNDCGAN

まずはCIFAR-10におけるSNDCGANの結果を見てみましょう。損失関数はヒンジ損失を使っています。ハイパーパラメータは$\lambda_\mathrm{real}=\lambda_\mathrm{fake}=10$, $\sigma_\mathrm{noise}=0.03$, $\lambda_\mathrm{dis}=5$, $\lambda_\mathrm{gen}=0.5$となっています。評価方法はFIDなので、小さければ良い結果です。まず、CRが今までの正則化手法と比べて大きく差をつけていることがわかります。そして、このCRをbCRとzCRがさらに改善させていることもわかります(bCRがベスト)。Inception Score(大きいと良い)も見てみると、同じような傾向になっていることがわかります。CRファミリーすごいですね。

2.2.2 CIFAR-10におけるResNet-SNDCGAN

続いて、ResNetによってスケールアップさせたSNDCGANでのCIFAR-10における結果を見てみます。ここではnon-saturating損失関数(つまり、オリジナルGANで提案された損失関数)を使っています。ハイパラは$\lambda_\mathrm{real}=10$, $\lambda_\mathrm{fake}=5$, $\sigma_\mathrm{noise}=0.07$, $\lambda_\mathrm{dis}=20$, $\lambda_\mathrm{gen}=0.5$となっています。こちらでもCRファミリーの凄さが見て取れます(zCRがベスト)。ISも同様の傾向を示しています。

2.2.3 CelebAにおけるSNDCGAN

CelebAにおける結果も見てみましょう。モデルはSNDCGANを用いており、損失関数はnon-saturating損失関数となっています。ハイパラは$\lambda_\mathrm{real}=\lambda_\mathrm{fake}=10$, $\sigma_\mathrm{noise}=0.1$, $\lambda_\mathrm{dis}=10$, $\lambda_\mathrm{gen}= $となっています。CRファミリーがやっぱりすごいです。bCRがベストですね。ISも同様です。

2.2.4 ICRによる実験

ついにbCRとzCRを組み合わせたICRの登場です。ここにbCRとzCRの結果を一緒にまとめていないのが謎ですが、上述したbCRとzCRの結果と比べてもICRが最も良いことがわかります。ISでもICRがベストですね。(ただ、bCR/zCR単体と比べるとISにおいてはICRが必ずしもベストとは言い難いように見えます。)

2.3 条件付き画像生成

今度はラベル情報も用いている条件付き画像生成について見てみます。データセットはCIFAR-10とImageNetを用いており、モデルはBigGANになっています。BigGANでもいずれのデータセットでもICRが見事に大きく性能向上させています。ハイパラは$\lambda_\mathrm{real}=\lambda_\mathrm{fake}=10$, $\sigma_\mathrm{noise}=0.05$, $\lambda_\mathrm{dis}=20$, $\lambda_\mathrm{gen}=0.5$となっています。

2.4 アブレーションスタディ

アブレーションスタディとしてbCRとzCRのハイパラの値を変えた場合の結果をまとめています。

2.4.1 bCRのハイパーパラメータ

bCRのハイパーパラメータは、リアル画像と生成画像それぞれへのCRの強さを決定する$\lambda_\mathrm{real}と\lambda_\mathrm{fake}$の2つです。SNDCGAN、CIFAR-10、ヒンジ損失関数における各ハイパラでの結果をヒートマップでまとめてくれています。FIDなので青ければ青いほど良いです。ここから言えるのは次の2つです。

リアル/フェイク片方にだけCRをする(=いずれかのハイパラをゼロにする)のは圧倒的に良くない。
両方とも同じような値であれば良い性能を示す。

2.4.2 zCRのハイパーパラメータ

zCRのハイパーパラメータは、入力ノイズに加算するガウシアンノイズの分散$\sigma_\mathrm{noise}$とGとDにおける損失関数での$\lambda_\mathrm{gen}$と$\lambda_\mathrm{dis}$の計3つです。$\lambda_\mathrm{gen}$は中程度(=0.5)の大きさで$\lambda_\mathrm{dis}$は大きい値(=20)で一番いい性能を示しています。(bCRのアブレーションで行なっていたような、ハイパラのお互いの関係性に関する実験は特に記述がありませんでした。)

3. まとめと所感

GANにおけるConsistency Regularizationはシンプルであるのにもかかわらず威力がすごいです。ICRに関しては少し疑問符(ICRはbCRやzCR単体とあまり変わらないのではないかという疑問。)ですが、少なくともbCR(もしくはzCR)だけでも使っておけば大きなゲインが得られると思っています。実際に自分で試してみてもbCRは如実に性能を上げてくれました。やっぱりCRってすごいんですね。こちらではbCRで他のDAを使った場合の結果がまとめてありますのでそちらもぜひご覧ください。bCRもzCRもとても簡単な実装で性能があがるのでぜひ試してみてはいかがでしょうか！

Twitterで人工知能のことや他媒体で書いている記事などを紹介していますので@omiita_atiimoもご覧ください。

こちらもどうぞ：

4. 参考

"Consistency Regularization for Generative Adversarial Networks", Zhang, H., Zhang, Z., Odena, A., Lee, H., (ICLR'20)
原論文
"Improved Consistency Regularization for GANs", Zhao, Z., Singh, S., Lee, H., Zhang, Z., Odena, A., Zhang, H., (2020)
原論文2。本記事ではこちらがメインです。
Improved Consistency Regularization for GANs
(YouTube) 原論文2の解説動画。