はじめに
Juliaを触り始めて、数式との相性が大変良い、計算がそこそこ速いという特徴から、シミュレーション向きではと思い始めています。
そこで、いわゆるイジングモデルの計算をしてみました。イジングモデルについては、色々な方が記事を書いておられます。
所詮n+1番煎じなのですが、せっかくなので、”非正方格子”を扱ってみたいと思います。計算にはMCMCを使います。
(2020/7/17追記) 続編記事を書きました。諸々のテクニックでJuliaコードを高速化してみたら50倍以上速くなった件
イジングモデル(Ising Model)
電子のスピン(z-スピン)の相互作用によって、エネルギー状態が変わるモデルとして知られています(例えば、こちら)。
E = - \frac{1}{2}\sum_i \sum_{j \neq i} J_{ij} s_i \cdot s_j - \sum_i B_i s_i
第1項に$\frac{1}{2}$を掛けている理由は、$(i,j)$のペアが必ず2回現れるので平均化する目的です。ここで、記号は以下の通りです。
- $E$ : 系全体のエネルギー。波動関数に作用する演算子の場合はハミルトニアン。
- $s_i$ : $i$番目の原子の(不対電子の)スピン(z軸)。$s_i = +1, -1$の2値をとる(パウリ行列$\sigma_z$の固有値)。
(※)以後、面倒なので不対電子を省略します。 - $N$ : 原子の個数。
- $J_{ij}$ : $i$番目の原子と$j$番目の原子の相互作用係数。
- $B_i$ : $i$番目の原子の外部磁場による作用係数。
このように書くとシンプルなのですが、近年注目されている量子コンピュータとも大変深い関連があります。
量子ゲート方式は、z-スピンだけでなく、xやy方向のスピンも考慮します。2次元の複素ベクトルで表される、いわゆるqubitを並べ、ゲート(論理演算)による相互作用によって所与のユニタリ演算子(の固有値など)に対応した物理量を確率的に計算することができるらしいです。
量子アニーリング方式は、z-スピンを0/1のbitとして扱います。相互作用と外部磁場を使って、2次形式で表されるような組み合わせ最適化問題(例えば、巡回セールスマン問題)を高速に解くことができるらしいです。
ですので、イジングモデルは大変重要な物理現象のモデルと言えます。
正方格子のイジングモデルについては、2次元で外部磁場がない条件のもとで厳密解が得られるようです。( 2次元 Ising モデルの厳密解 - NIMS)
格子を定義
イジングモデルでは、原子と原子の相互作用が本質的に重要です。相互作用は、隣接する原子同士で作用すると考えられるので、配置を定義する必要があります。
一番分かりやすいのが下図左の正方格子です。
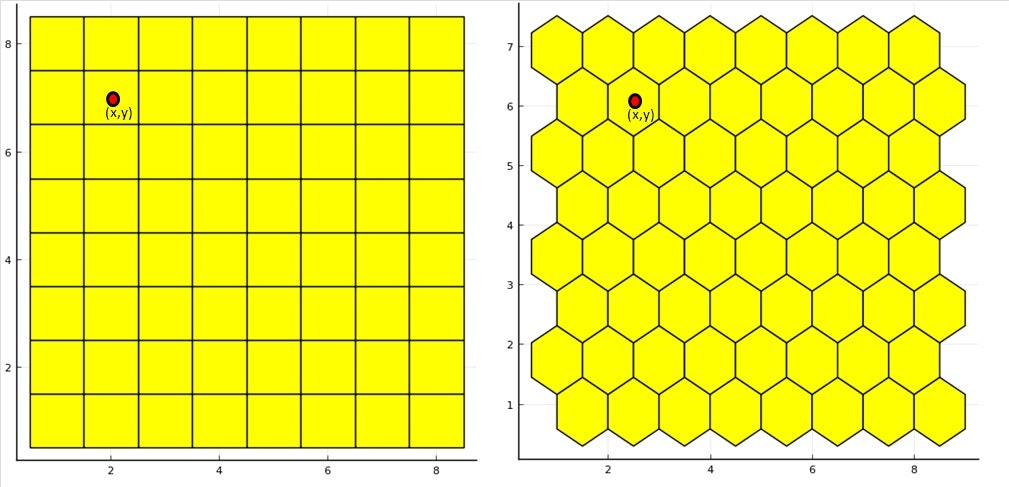
この場合、格子の中心位置$(x,y)$にある原子は
$(x-w,y), (x,y-h), (x+w,y), (x, y+h)$にある4つの原子
と相互作用します。$w=h$は格子の幅ですね。
次に、図右の六角形の格子(六方最密充填構造の格子)を考えてみましょう。この場合、格子の中心位置$(x,y)$にある原子は
$(x-2w,y), (x-w,y-3/2h), (x+w,y-3/2h), (x+2w, y), (x+w, y+3/2h), (x-w, 3/2y)$にある6つの原子
と相互作用します。ただし、$h=\frac{2}{\sqrt{3}}w$とします。
MCMC
MCMC(Markov Chain Monte Carlo method)は、ある確率分布の標本を効率的に生成して、標本から確率分布の性質を推定する手法です。マルコフ連鎖が確率分布に従う標本の生成を、モンテカルロが標本からの推定を担うわけです。MCMCについては伊庭先生の動画が大変分かりやすいです。
イジングモデルにMCMCを適用する場合、各原子のスピン状態を
S = \left( s_1,s_2,\cdots ,s_N \right)
と置いたとき、エネルギー$E=E(S)$が実現する確率が次のボルツマン分布に従うと仮定します(ボルツマン定数$k_B$は省略します)。
Pr(E(S)) = \frac{exp(-E(S)/T)}{Z},\ Z=\sum_S exp(-E(S)/T)
ここで、$T$は温度、$Z$は分配関数(規格化関数)です。温度$T$が低いほど、$E(S)$の違いが強調され、温度$T$が高いほど、$E(S)$の違いが影響しにくくなります。また、エネルギー$E(S)$が低い状態$S$ほど実現する確率が高いわけです。
Metropolis基準を用いたMCMCでは、
S \rightarrow S_{new} \mathrm{\ with\ prob.\ } \frac{Pr(E(S_{new})) }{Pr(E(S))}
となる訳ですが、ボルツマン分布が指数分布であるおかげで、
\begin{eqnarray}
\frac{Pr(E(S_{new})) }{Pr(E(S))}
&=& exp\left( - \frac{E(S_{new}) - E(S)}{T} \right) = exp( - \Delta E/T)\\
\Delta E &=& E(S_{new}) - E(S)
\end{eqnarray}
と計算でき、さらに、$S_{new}$と$S$の差が$i$番目の原子のスピンのみであるというGibbsサンプリングに従う場合、$\Delta E$は次式で書けます。
\Delta E = s_i \left( \sum_{j \in Ne(i)} ( J_{ij} + J_{ji} ) s_j + 2 B_i \right)
ここで、$Ne(i)$は原子$i$に隣接する原子の番号です。
つまり、"隣接"さえ定義してあげれば簡単に$\Delta E$や$Pr(E(S_{new})) / Pr(E(S))$が計算できるので、MCMCを高速に回すことができる訳です。"隣接"の定義は格子の形で決まるので、格子によって隣接関数$Ne(i)$を変えてやれば色々な格子で計算できるはずです。
Juliaでシミュレーション
では、具体的にJuliaで計算してみましょう。
方針
まず、方針として次を考えます。
- 色々な格子を定義しても使えるようにする。
- 相互作用の強度$J_{ij}$や外部磁場$B_i$も自由に定義したい。
- モジュールを適度に切り分ける。
以上をJuliaで実現するため、ファンクターパターンを使うことにしました。
ソースコード
ソースコードは全部で3つのパートで構成しました。
全体はGitHubにアップロードしてあります。
1.格子定義パート
格子を定義するモジュールです。六角格子での定義を載せます。ファンクターではパラメータdを受け取って、(getNeighbors, genPoly)の2つの関数を返します。
関数の意味は次の通りです。
- $getXY : k \rightarrow (x,y) $ : k番目の格子の(x,y)座標を計算。
- $getK : (x,y) \rightarrow k $ : 格子の(x,y)座標から番号kを計算。
- $getNeighbors : k \rightarrow Ne(k)$ : k番目の格子の近接格子の番号リストを返す。
- $genPoly : k \rightarrow (xs,ys)$ : k番目の格子を表すポリゴン座標を返す。
module HexaLatticeModel
mutable struct ParamDict
nrows::Int
ncols::Int
N::Int
end
function genFunctor(d)
d = d
# cell size
w = 0.5
h = 2w/sqrt(3)
function roundN(n, N)
m = (n - 1 + N) % N
m + 1
end
function getXY(k, d=d)
m = roundN(k, d.ncols)
n = roundN(div(k-1, d.ncols)+1, d.nrows)
if n % 2 == 1
x = m + 0.5
y = n*(1.5h)
else
x = m
y = n*(1.5h)
end
(x, y)
end
function getK( x, y, d=d)
# must round each x, y
n = (round(Int,y/(1.5h)) - 1 + d.nrows) % d.nrows + 1
#
if n % 2 == 1
xn = Int(x - 0.5)
else
xn = Int(x)
end
m = (xn - 1 + d.ncols) % d.ncols + 1
k = (n - 1) * d.ncols + m
end
function getNeighbors( k, d=d)
(x, y) = getXY(k, d)
[getK(x-2w, y, d), getK(x+2w, y, d),
getK(x- w, y-1.5h, d), getK(x+ w, y-1.5h, d),
getK(x- w, y+1.5h, d), getK(x+ w, y+1.5h, d)]
end
# polygon for each cell
function genPoly(k, d=d)
(x, y) = getXY(k, d)
(x .+ [ -w, 0, w, w, 0, -w, -w],
y .+ [ h/2, h, h/2, -h/2, -h, -h/2, h/2])
end
return (getNeighbors, genPoly)
end # of functor
end # of module
2.MCMCパート
MCMCを計算するモジュールです。ファンクターでは(getJ, getB)の2つの関数を
受け取って、(E, MCMC)の2つの関数を返します。
MCMCの速度を上げる工夫として、Gibbsサンプリングする位置と乱数を予めリスト化しておいています。
module IsingMCMC
function genFunctor( getJ, getB)
getJ = getJ
getB = getB
# E(S) = - 1/2\sum_{i,j, i not j} J_{i,j} si sj - \sum_i B_i si
function E(S, N)
Et = 0
for i in 1:N
J = Main.getNeighbors(i)
Et += -0.5*S[i]*sum( [getJ(i,j) * S[j] for j in J] )
Et += - S[i]*getB(i)
end
Et
end
# differential energy
function dE(S, k, N)
dEt = 0
J = Main.getNeighbors(k)
dEt += S[k]*sum( [(getJ(k,j) + getJ(j,k)) * S[j] for j in J] )
dEt += 2*S[k]*getB(k)
dEt
end
# probability for dE
PrE(dE, T) = exp(-dE/T)
# flip spin at x
function flipx!(list, x)
list[x] *= -1
end
# MCMC
function MCMC( T, N, trial)
# initialize
sim = []
S = ones(N)
for i in 1:N
if rand() < 0.5
flipx!(S,i) # random flip at first
end
end
# Gibbs sampling position
gpos = [rand(1:N) for i in 1:trial]
# random value in [0,1]
rn = [rand() for i in 1:trial]
# MCMC trial
for t in 1:trial
k = gpos[t]
de = dE(S, k, N)
if rn[t] < PrE(de, T) # MH criteria
flipx!(S, k) # change k
end
push!(sim, copy(S))
end
sim
end
return (E, MCMC)
end # of functor
end # of module
3.メインパート
計算のメインの部分です。
mainの第1引数は格子のタイプ(1:正方格子,1:六角格子)、第2引数は温度です。
格子のタイプに応じて、モジュールを切り替えてファンクターから関数を受け取りグローバルに設定しています。また、$J_{ij}, B_i$はメインパートのグローバル関数で定義します。
Plots.plotにShape型([xs,ys])を渡せばポリゴンも描画できるようです。ただし、plotをループ内で呼ぶと非常に遅いので、複数のポリゴンを一旦結合してからループ外で描画しています。
# load packages
using Plots
gr()
# load modules
# select a model later
include("HexaLatticeModel02a.jl")
include("SquareLatticeModel02a.jl")
# MCMC
include("IsingMCMC02a.jl")
###################################################################################################
# view functions
function drawEnergy(sim, trial, T, d=d, N=N)
xs = [t for t in 1:1000:trial]
ys = [E(sim[t],N) for t in xs]
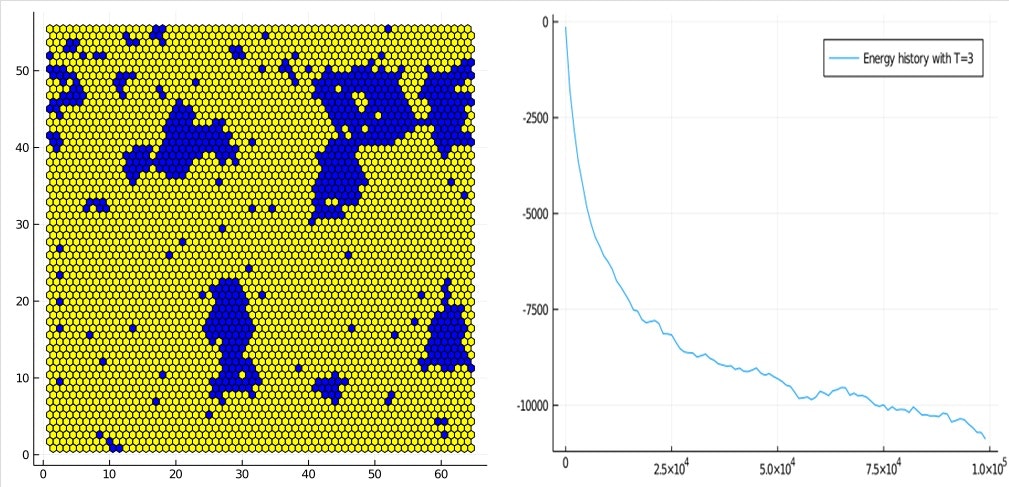
p = Plots.plot(xs, ys, label="Energy history with T=$(T)")
end
function drawSim(sim, f, d=d, N=N)
snap = sim[f]
p=Plots.plot([],[],legend=false, size=(500,500))
p0xs = [];p0ys = []
p1xs = [];p1ys = []
for i in 1:N
# bits
(xs,ys) = genPoly(i, d)
if (snap[i] == 1) # up-spin
p1xs = vcat(p1xs, NaN, xs)
p1ys = vcat(p1ys, NaN, ys)
else # down-spin
p0xs = vcat(p0xs, NaN, xs)
p0ys = vcat(p0ys, NaN, ys)
end
end
poly0 = Shape(p0xs, p0ys) # creating polygon
p = Plots.plot!(poly0, fillcolor = plot_color(:blue) ,legend=false)
poly1 = Shape(p1xs, p1ys)
p = Plots.plot!(poly1, fillcolor = plot_color(:yellow),legend=false)
end
###################################################################################################
# prepare
# setting for energy function
function getJ(i, j, d=d)
J0 = 1
(j in getNeighbors(i,d)) ? J0 : 0
end
function getB(i, d=d)
B0 = 0
##B0 = (i % 40 == 0) ? 10 : 0
B0
end
###################################################################################################
# do simulation
# setting for model
d = SquareLatticeModel.ParamDict(64,64,0)
# d = SquareLatticeModel.ParamDict(32,32,0)
# d = SquareLatticeModel.ParamDict(8,8,0)
N = d.nrows * d.ncols
d.N = N
# main function
# mdlno: 1(square), 2(hexa)
# T: temperature e.g. T=2.26
function main(mdlno, T)
# setting for simulation
trial = 100000 # MCMC trial
# gen functors as global
global getNeighbors, genPoly
if mdlno == 1
(getNeighbors, genPoly)= SquareLatticeModel.genFunctor(d)
elseif mdlno == 2
(getNeighbors, genPoly)= HexaLatticeModel.genFunctor(d)
end
# simulation
global E, MCMC
(E, MCMC) = IsingMCMC.genFunctor(getJ, getB)
print("start MCMC...")
@time sim = MCMC(T, N, trial);
# save images
# energy history
print("start drawEnergy...")
@time p = drawEnergy(sim, trial, T)
Plots.savefig(p, "Ising_energy_M$(mdlno)_T$(T).png")
# cell state
print("start drawSim...")
@time p = drawSim(sim, trial, d)
Plots.savefig(p, "Ising_sim_M$(mdlno)_T$(T).png")
print("done.")
end
###################################################################################################
上記の3つのソースを保存して、Juliaを起動し下記を実行してください。
julia> include("IsingSimMain02a.jl")
julia> main(2,1)
シミュレーション結果
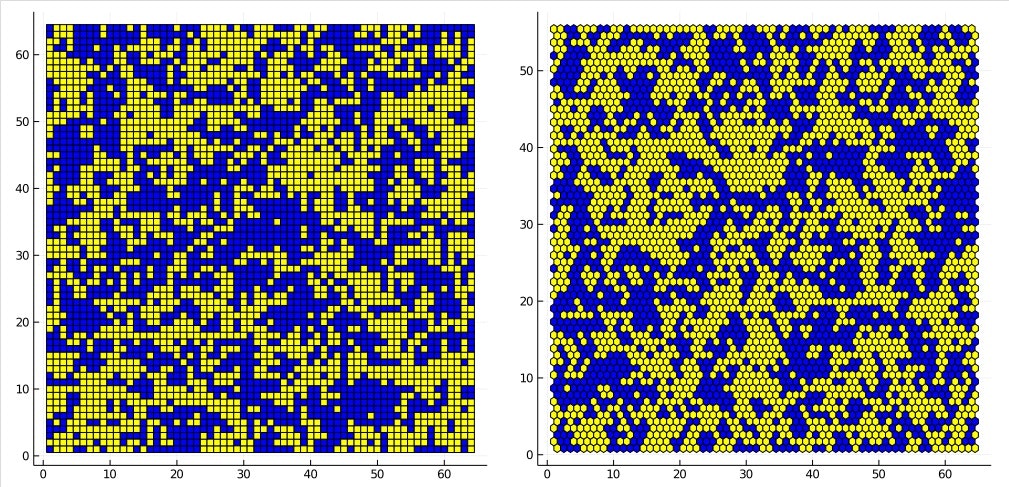
まず、$J_{ij}=1, B=0$の場合を見てみます。
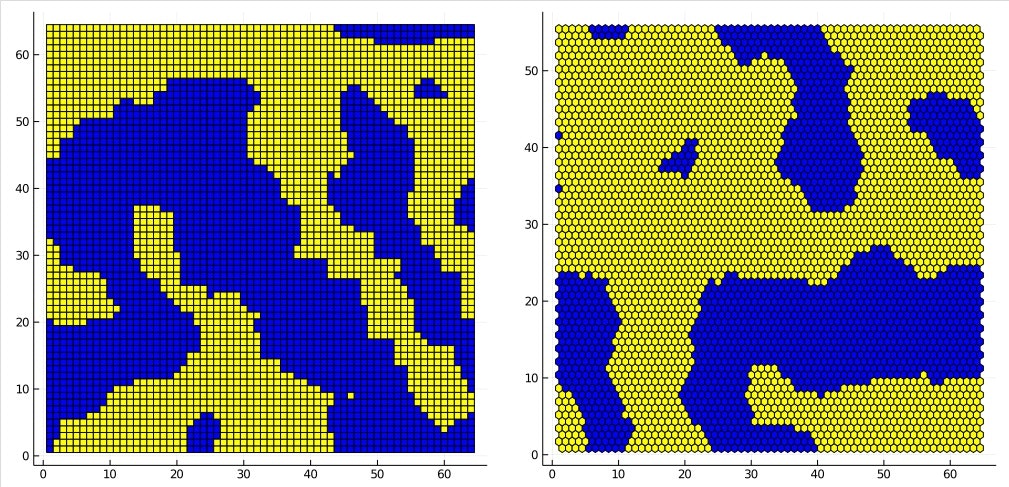
温度T=1
左が正方格子、右が六角格子です。スピンの上下でくっきり領域が分かれます。正方格子の場合は所々に四角形領域が見えます。
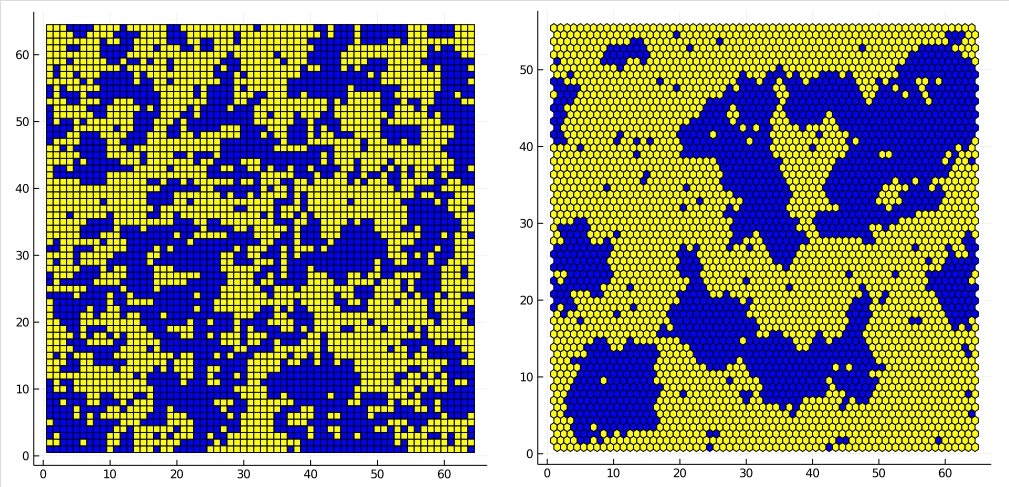
温度T=3
正方格子ではかなり乱れていますが、六角格子ではまだ領域が明確です。
相転移温度
相転移が起こる温度は$Tc = z J / k_B$ (zは隣接原子の数)と言われているので、正方格子では$T=4$, 六角格子では$T=6$としています。相転移温度ではスピンの期待値が0になるので、ほぼランダムな状態となっています。
おまけ
外部磁場作用係数$B_{i}$を少し変わった値にしてみましょう。
function getB(i, d=d)
B0 = (i % 40 == 0) ? 10 : 0
B0
end
つまり、40個に1個は強く外部磁場の影響を受けるようにします。
温度$T=3$のとき、次のようになりました。適当に外部磁場の影響を受けやすい原子を混ぜておくと磁化しやすくなるようですね。
Juliaで書いてみた感想
オブジェクト指向言語のようにクラスに相当する仕様がないので、格子を切り替える部分は、C++なら抽象クラスと継承使うのにな~と思ったのですが、ファンクターを使えばある程度何とかなるようです。
ここで、ファンクターは本記事では以下の意味で使ってます。全然厳密な定義ではないので注意してくださいね。
f: (p \rightarrow a) \rightarrow ( g(p,x) \rightarrow g(p=a,x) )
ただし、ファンクターではメンバ変数が持てない(モジュール変数が書き換えられない)ため、クラスのような柔軟性はありません。
まあ、関数型言語の思想として副作用をできるだけ排除するのが正しい在り方とも言えるので、しょうがないですが。
また、ガベージコレクションの動きが気になります。場合によってはGC timeが数十%にもなることがあるようです。これも書き方で回避できるのでしょうか。
参考リンク
下記のページを参考にさせて頂きました。