メトロポリス・ヘイスティングス法(M-H algorithm)によるイジングモデルのスピンマップ生成

#はじめに
二次元正方格子イジングモデルのスピンマップを温度ごとにメトロポリス・ヘイスティング法で作成したのでまとめる。
イジングモデルについては簡略化した説明しかしてないので、詳しく知りたいのであれば統計力学の教科書を参照して欲しい。
この方法で正方格子以外の三角格子などのスピンマップも作成できるので是非試して欲しい。（ハミルトニアン変化を変えるだけ）

メトロポリス・ヘイスティング法(Metropolis-Hastings algorithm)

メトロポリス・ヘイスティングス法は、直接サンプリングが困難な確率分布からランダムサンプルのシーケンスを得るためのマルコフ連鎖モンテカルロ法（MCMC）であり、統計学や統計物理学でよく使われている。このシーケンスは、分布の近似や積分、期待値を計算するために使用することができる。
###アルゴリズム
任意の初期状態を設定し、下記方法で更新を繰り返し、最終的な状態を尤もらしい状態として採用する。
ある状態$S$が採択されているとする。更新の候補として確率密度関数$g(\acute{S}\mid S)$に従って状態$\acute{S}$を生成する。$g(\acute{S}\mid S)$は状態$S$が状態$\acute{S}$に移る確率の分布関数である。ここで状態の尤度(起こりやすさ)を$P(S)$とし、新たな関数$$a_1 = \frac{P(\acute{S})}{P(S)}、a_2=\frac{g(S\mid \acute{S})}{g(\acute{S}\mid S)}$$$$a = a_1a_2$$を導入する。$a_1$は尤度比（起こりやすさの比率）で$a_2$は確率密度関数の比である。状態$S$は$a$を用いて以下のルールに従って状態を更新する。
・$a \ge 1$のとき状態$S$を状態$\acute{S}$に更新して次のステップに進む。
・$a \lt 1$のとき確率$a$で状態$S$を状態$\acute{S}$に更新して次のステップに進み、確率$1-a$で状態を更新させずに次のステップに進む。
更新は状態が完全に更新されなくなるまで繰り返す。

##イジングモデル(Ising Model)
イジングモデルは主に強磁性体の模型として使用されるモデルである。(強磁性体特有のモデルというわけではなく、様々な現象のモデルとして活躍する。)
このモデルは注目する格子点とその再隣接格子点との相互作用のみを扱う理論である。このような単純な理論であるが、相転移現象を記述することができる優れたモデルである。
このモデルのハミルトニアンは外力が無ければ$$
H = -J\sum_{<i,j>}\sigma_i\sigma_j
$$によって求められる。ここでJは交換相互作用エネルギー、$<i,j>$は隣接格子点の組み合わせ、$\sigma_k$は格子点kでのスピンの値である。イジングモデルの尤度はハミルトニアンを用いて表され、系のハミルトニアンが$H$、温度がTで与えられた時$\frac{\exp(\frac{H}{k_BT})}{Z_\beta}$と表される。つまり状態が変化することによるハミルトニアン変位を$\Delta H$としたとき、$a_1=\exp(\frac{\Delta H}{k_BT})$となる。また、更新の候補をランダムに選ばれた一つの格子点のスピンを反転した状態とすると、どの状態からどの状態に遷移しても確率は一定となる。つまり遷移の向きによって確率密度は変わらないので$a_2=1$よって$a=a_1=\exp(\frac{\Delta H}{k_BT})$となる。

二次元正方格子イジングモデル

格子状に張り巡らされた空間の格子点に電子があるモデルを二次元正方格子イジングモデルという。このモデルのハミルトニアンは$J=1$とすると$$
H = -\sum_{<i,j>}\sigma_i\sigma_j
$$
と表せる。(これはどの格子でも変わらない。)これを用いてある一点$(k,l)$のスピンの値が反転した時のハミルトニアンの変化を求めると$$
\Delta H = -\sum_{i=0}^{1}(\sigma_{k,l}\sigma_{k+2i-1,l}+\sigma_{k,l}\sigma_{k,l+2i-1})
$$
となる。(これは格子によって変わる。)
この時周期境界条件として$\sigma_{N,j}=\sigma_{0,j}、\sigma_{-1,j}=\sigma_{N-1,j}、\sigma_{i,N}=\sigma_{i,0}、\sigma_{i,-1}=\sigma_{i,N-1}$を設けた。
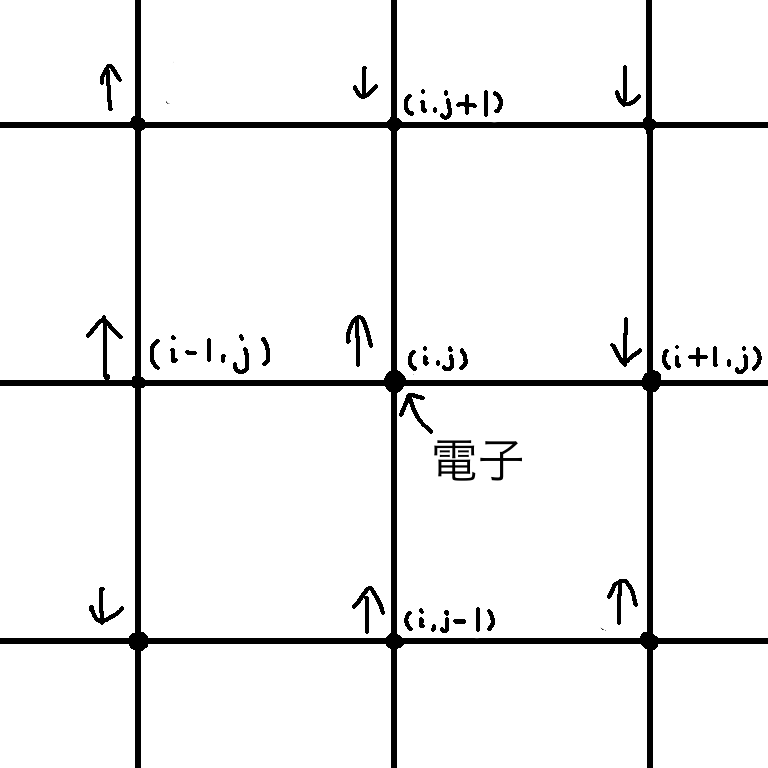例として左図のような系を考え、格子点(i,j)を反転させたときハミルトニアンはどれほど変化するかを求める。先述の通りイジングモデルでは最隣接格子点のみ考えるので、格子点(i,j)が反転することでスピンの商が変わる格子点の組み合わせは(i,j)と(i+1,j)、(i,j)と((i-1,j)、(i,j)と((i,j+1)、(i,j)と((i,j-1)それぞれ4つのみである。幸いスピンの値は1、-1のみを取るので、ハミルトニアン変化は$$\Delta{H}=2(\sigma_{i,j}\sigma_{i+1,j}+\sigma_{i,j}\sigma_{i-1,j}+\sigma_{i,j}\sigma_{i,j+1}+\sigma_{i,j}\sigma_{i,j-1})$$の簡単な形式で表せる。

実装

実装はPythonによって行った。
コード全体は以下のようになっている。

GenerateSpinState.py

import numpy as np

class GSS:
    def __init__(self, N, T):
        # lattice size
        self.N = N
        # temperature list
        self.T = T
        # generate N*N spin state by random
        self.state = 2 * np.random.randint(0, 2, (self.N, self.N)) - 1

    # calc hamiltonian displacement　which is square lattice, after flipping one site(x,y)
    def calc_Hamiltonian_square(self, x, y):
        delta_H = 2 * self.state[x, y] * (self.state[(x+1)%self.N, y] + self.state[x, (y+1)%self.N] + self.state[(x-1)%self.N, y] + self.state[x, (y-1)%self.N])
        return delta_H

    # flip random spin site
    def flip_spin(self):
        new_state = self.state.copy()
        [x, y] = np.random.randint(0, self.N, (2))
        new_state[x, y] *= -1
        return new_state, x, y

    # calc specious spin state by metropolis method
    def calc_spin_state(self, t):
        n = 10000
        for i in range(n):
            # get flip site
            new_state, x, y = self.flip_spin()
            # calc hamiltonian displacement
            deltaH = self.calc_Hamiltonian_square(x, y)
            # decide whether to adopt
            if np.random.rand() <= np.exp(-deltaH/t):
                self.state = new_state

    def calc_each_temperature(self):
        # save spin state
        X = []
        for t in self.T:
            # init spin state
            self.state = 2 * np.random.randint(0, 2, (self.N, self.N)) - 1
            # generate spin state which temperature t
            self.calc_spin_state(t)
            # append generate spin state which temperature t
            X.append(self.state)
        return np.array(X)

main.py

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib.animation import FuncAnimation

import GenerateSpinState

# save path
# train test data
npy_path = "./result//"
# spin map
spin_map_path = "./result/"


# lattice size
N = 32

# number of data (square lattice)
count = 100

# temperaturelist/Significant digits is 3
T_list = np.linspace(0.1, 5.5, count).round(3)

# make gif which write spin state transition
def create_spinmap_gif(data, T, save_path):
    save_path = save_path + "squarelattice.gif"
    fig = plt.figure()

    def Plot(num):
        plt.cla()
        plt.imshow(data[num])
        t_len = len(str(T[num]))
        title = "temperature:" + str(T[num]) + "0"*(5-t_len)
        plt.title(title)

    anim = FuncAnimation(fig, Plot, frames=100)
    anim.save(save_path, writer='imagemagick')


# call module GSS
GSS = GenerateSpinState.GSS(N, T_list)

# create spin map
X_train = GSS.calc_each_temperature()

# create gif
create_spinmap_gif(X_train, T_list, spin_map_path)

まずGenerateSpinState.pyについての説明をする。
格子の大きさ、温度をインスタンス変数とする。またスピンマップの初期状態を生成する。

def __init__(self, N, T):
    # lattice size
    self.N = N
    # temperature list
    self.T = T
    # generate N*N spin state by random
    self.state = 2 * np.random.randint(0, 2, (self.N, self.N)) - 1

任意の格子点$(x,y)$のスピン値が反転したときのハミルトニアン変化$\Delta H$を求める。イジングモデルの特徴として再隣接格子点のみ計算に反映するので、反転した格子点周りの格子点のみ取り出して計算するだけで良い。

# calc hamiltonian displacement　which is square lattice, after flipping one site(x,y)
def calc_Hamiltonian_square(self, x, y):
    delta_H = 2 * self.state[x, y] * (self.state[(x+1)%self.N, y] + self.state[x, (y+1)%self.N] + self.state[(x-1)%self.N, y] + self.state[x, (y-1)%self.N])
    return delta_H

格子点を一つランダムに選び、その一点を反転させたスピンマップをnew_stateとして更新の可否が決まるまで保存する。反転前のスピンマップとしてself.stateをnew_stateに移すときに.copy を忘れないようにする。.copy がないとnew_stateを更新するとself.stateも更新されてしまいスピンマップが更新し続ける。

# flip random spin site
def flip_spin(self):
    new_state = self.state.copy()
    [x, y] = np.random.randint(0, self.N, (2))
    new_state[x, y] *= -1
    return new_state, x, y

上2つの関数を呼び出した後$\exp{\frac{\Delta{H}}{k_B\beta}}$の確率でnew_stateを採用して状態の更新を行っている。採用されなければ状態は更新しない。繰り返し数として10000としているが物理的、数学的根拠はなく、キリの良い値だったので設定した。結果として偶然最もらしい結果を得られたので採用している。(1000回では完全に更新されなかった。)

# calc specious spin state by metropolis method
def calc_spin_state(self, t):
    n = 10000
    for i in range(n):
        # get flip site
        new_state, x, y = self.flip_spin()
        # calc hamiltonian displacement
        deltaH = self.calc_Hamiltonian_square(x, y)
        # decide whether to adopt
        if np.random.rand() <= np.exp(-deltaH/t):
            self.state = new_state

最初に取得した調べたい温度が格納されているリストself.T様々な温度でスピンマップを作成した。

def calc_each_temperature(self):
    # save spin state
    X = []
    for t in self.T:
        # init spin state
        self.state = 2 * np.random.randint(0, 2, (self.N, self.N)) - 1
        # generate spin state which temperature t
        self.calc_spin_state(t)
        # append generate spin state which temperature t
        X.append(self.state)
    return np.array(X)

これにてGenerateSpinState.pyの説明は終わった。次にmain.pyであるが、格子のサイズ、温度の配列を設定し、GenerateSpinState.pyを呼び出すことで温度後とのスピンマップを入手している。このケースでは格子のサイズは36であり、温度の配列は0.1~5.5を100等分したものである。温度の配列は理論相転移温度が2.26であることを考慮して作成した。create_spinmap_gifで以下のようなgif画像を作った。(各温度で採用されたスピンマップ)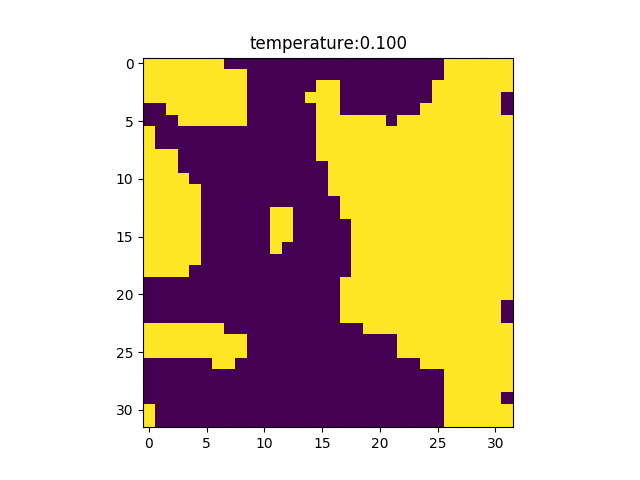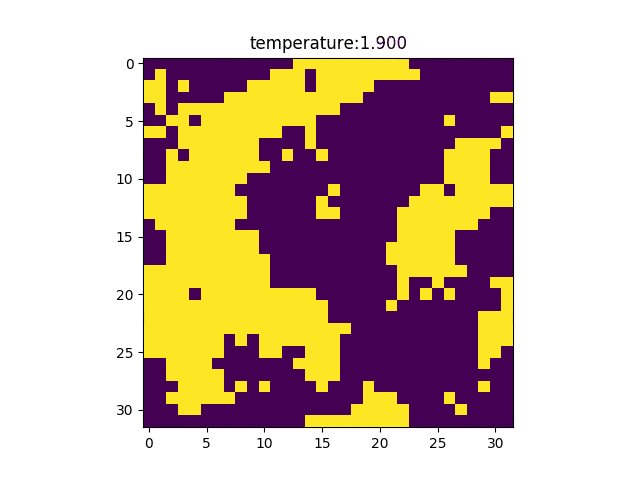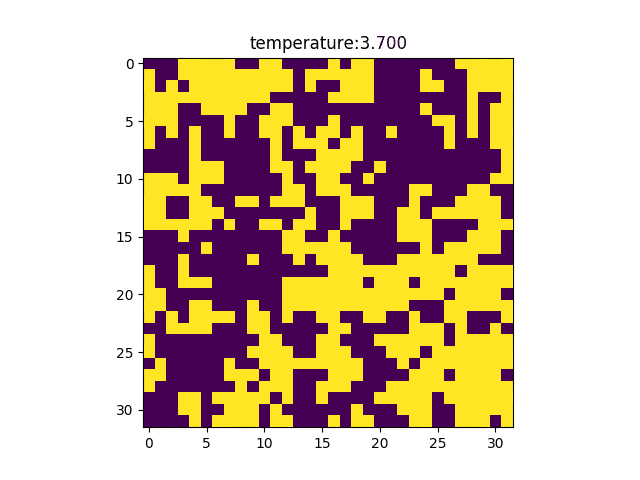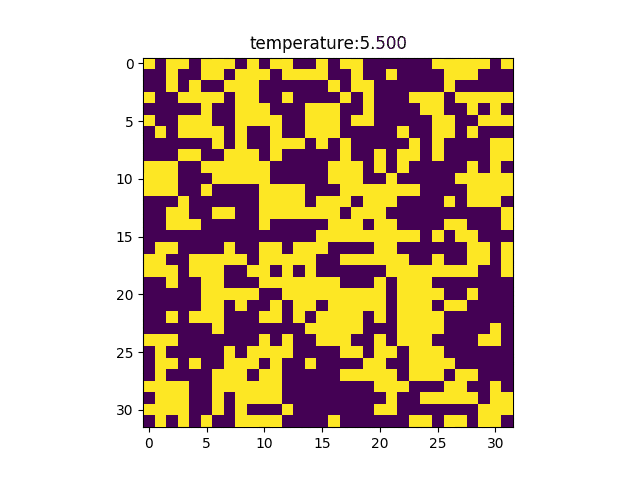

参考文献

Metropolis–Hastings algorithm
Hastings, W.K. (1970). "Monte Carlo Sampling Methods Using Markov Chains and Their Applications".