はじめに
色々な観測データを集めた結果、その観測値の背後にあるであろう確率分布を、モデルに当てはめて推定してみたいという欲求が出てくることがあります。各種の統計量の計算やシミュレーション計算に便利ですからね。確率分布のモデルとして、正規分布、指数分布、2項分布、ベータ分布等ありますが、今回、ガンマ分布を対象として、MCMC法(Markov Chain Monte Carlo method)をその原理から"素朴に"実装しつつ、どのくらいフィッティングできるかを試してみたいと思います。なお、MCMCを実行する優れたツールとして、WinBUGSやPyMC3などがありますので、敢えて自分で作る必要はないでしょう。とはいえ、自分で作ることで色々見えてくるものもあり、理解が進むメリットはあるのかなと思います。
ガンマ分布とは?
ガンマ分布とは、形状パラメータ$k$、尺度パラメータ$q$の2つのパラメータで特徴付けられる分布です。
P(x) = \frac{1}{\Gamma(k)q^k}x^{k-1}e^{-x/q},\ x \geq 0 \ (k>0,\ q>0)
非負の実数をとる分布であり、指数分布やカイ2乗分布、あるいはアーラン分布なども表現できる優れた奴です。特に、裾の広い歪んだ分布を表現できる点がいいですね。世の中の観測データは、物の数、長さ、重さ、時間の間隔、人口、金額、など非負の値で表されるものが沢山あり、そういう変数の分布を表現するのに便利そうです。実際、待ち時間の分布や所得の分布など、工学や経済学で使われるようです。
MCMCとは?
MCMC法(Markov Chain Monte Carlo method)は、ある確率分布の標本を効率的に生成して、標本から確率分布の性質を推定する手法です。マルコフ連鎖が確率分布に従う標本の生成を、モンテカルロが標本からの推定を担うわけです。詳しいことは、統計数理研究所の伊庭幸人先生の解説動画が大変分かりやすいです。
今回の記事では、ガンマ分布の推定にMCMCを使っていくため、以下の言葉を定義します。
- $\theta$ : 推定したい$N$次元のパラメータ
- $P(x|\theta)$ : パラメータ$\theta$に従って計算される確率分布モデル(モデルなので自分は知っている)
- $X_1,X_2,...,X_n$ : 観測された標本値。ただし、独立性を仮定。
- $D_n=(X_1,X_2,...,X_n)$ : 観測されたデータ(値のセット)
- $P(\theta | D_n)$ : データ$D_n$から推定されるパラメータ$\theta$の確率分布
ここでやりたいことは、データ$D_n$を沢山集めて、パラメータ$\theta$の確率分布$P(\theta | D_n)$を上手く計算できれば、想定しているモデルのパラメータ$\theta$の(事後確率に基づく)期待値を計算できるよね、ということです。
確率分布$P(\theta | D_n)$は、ベイズの定理から(または確率分布の正規化条件から)、次式で表されます。
P(\theta|D_n) = P(D_n | \theta)P(\theta) / \int_{\theta} d\theta P(D_n | \theta)P(\theta)
ここで、積分はデータ$D_n$を生み出す確率が0でない全ての$\theta$について取る必要があります。
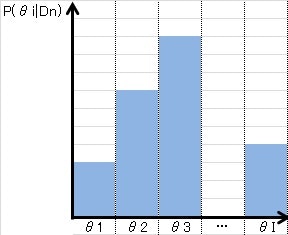
この分布推定を素朴に行う方法の一つが、グリッド計算です。つまり、$\theta$を適当なグリッドで均等にばらまいて離散値$\theta_i (i=1,2,...,I)$で代表してあげると、
P(\theta_i|D_n) \simeq P(D_n | \theta_i)P(\theta_i) / \sum_{j \in I} P(D_n | \theta_j)P(\theta_j)
のように、分母の積分を和で近似することができます。図で書くとこんな感じです。
しかしながら、$\theta$の推定精度を上げるには、離散値の数$I$を十分大きくとらなければいけません。単純に$N$次元のパラメータを$M$個のメッシュで表現しようとすると、$I=M^N$個の離散値が必要で、次元が上がるにつれ爆発的に増加してしまいます。
そこで、MCMCでは発想を変えて、離散値$\theta_i$を固定せずに、どんどん動かしてしまえ、ということをやります。動かす回数を$k(k=1,2,...)$、$k$回目の$\theta_i (i=1,..,I)$を$\theta_i(k)$, $\theta_i(k)$が従う確率分布を$P_k(\theta)$とします。また、$\theta_i(k)$から$\theta_i(k+1)$への動かし方を$\pi(x \rightarrow x')$とします。すると次のように図示できます。
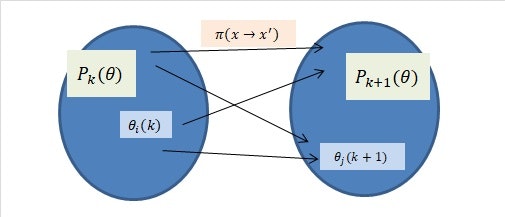
この動かし方$\pi(x \rightarrow x')$を上手いこと設計してあげて、何回も動かすうちに、
P_k(\theta) \rightarrow P(\theta | D_n) \ ({\rm as \ } k \rightarrow \infty)
が成り立てば、目的を達成することができますね。次に、この動かし方の一つとして、Metropolisアルゴリズムを見ていきます。
Metropolisアルゴリズム
Metropolisアルゴリズムとは、確率分布からのサンプリングアルゴリズムです。先ほどの図の中で、さらに登場人物を増やします。
- $P_*(\theta)$ : 推定したいモデルに従う分布(本記事の場合$P(\theta | D_n)$)
- $P_{o_k}(\theta)$ : $P_k(\theta)$の中で$P_*(\theta)$以外に従う分布
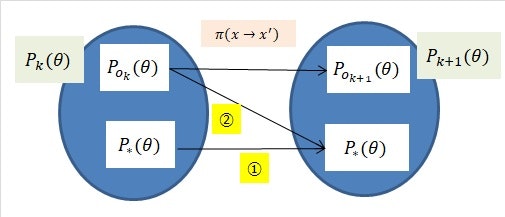
つまり、$\theta_i$がモデルに従う分布と従わない分布の合成で生成されているとしましょう。このとき、下図のように、写像$\pi(x \rightarrow x')$による移動が制限されるとしましょう。
つまり、$P_* (\theta)$に従っていた$\theta_i$はそのまま$P_*(\theta)$に必ず移動する、という制限です(図の①)。さらに、$P_{o_k} (\theta)$に従っていた$\theta_i$は$P_*(\theta)$にも必ず移動できる(図の②)としましょう。
すると、②がそこそこ存在すれば、①の制限から、$k$が増加するにつれて、$P_k(\theta) \rightarrow P_*(\theta)$になる様子が伺えます。
厳密には、①のことを定常性、②のことを既約性、といい、これら2条件から確率分布の収束が成り立つことをエルゴード性というらしい、です。(詳しくは伊庭幸人先生の解説動画を参照)。
これらの性質を満たす写像$\pi(x \rightarrow x')$の一つがMetropolisアルゴリズムで、以下のフローで表されます。
- 現在の点$x$とある対称な確率分布$Q(x,x')(=Q(x',x))$から$x'$を生成。
- 一様乱数$0 \leq r <1$を生成。
- $r < {P_* (x')}/{P_*(x)} $なら、$x \rightarrow x'$に移動。そうでないなら、移動しない($x \rightarrow x$)。
- 1から3を繰り返す。
1の確率分布は対称であればいいので、例えば正規分布が使えます。
Q(x,x') = \frac{1}{\sqrt{2\pi \sigma^2}}exp\left(-\frac{(x-x')^2}{2\sigma^2}\right)
ちなみに、対称でない($Q(x,x') \neq Q(x',x)$)場合へと拡張したアルゴリズムをMetropolis-Hastingsアルゴリズムと言います。
3のステップを見てみると、
- $P_* (x') \geq P_*(x)$なら必ずxからx'に移動します。つまり、より確率の高い方へ移動していきます。(上図の②に相当)
- $P_* (x') < P_* (x)$なら確率$P_* (x')$と$P_* (x)$の比に応じて、x'かxに移動します。(上図の①に相当)
Pythonで計算してみる
それでは、MCMCをPythonで実装していきながらガンマ分布の推定をしてみましょう。
1. 前準備
ライブラリの設定をします。
import numpy as np
import matplotlib.pyplot as plt
from math import gamma
ガンマ関数、ヒストグラムの生成、確率分布の形状を表示する関数を定義します。
def gamma_pdf(x, k, q):
p = 1./(gamma(k) * pow(q, k)) * pow(x, k-1) * np.exp( -x/q )
return p
def genPdfHist(f, xmin, xmax, N):
x = np.linspace(xmin,xmax, N)
p = [f(v) for v in x]
return x,p
def showPdf(f, xmin, xmax, N, yscale=1.0):
x, p = genPdfHist(f, xmin, xmax, N)
y = [e*yscale for e in p]
plt.plot(x,y)
plt.show()
2. 観測データを用意
次に、ガンマ分布を使って、観測データを作ってみます。観測データの作成のために、サンプリングする関数を定義します。
def PlainSampler(pdf, xmin, xmax, N):
n = 0
xs = []
while n < N:
x = xmin + np.random.rand()*(xmax-xmin)
p = pdf(x)
if np.random.rand() < p:
# accept
xs.append(x)
n = n + 1
return xs
上の関数を使って、観測データを生成します。(実験用の観測データという意味です)
まず、正解モデルのパラメータを$(k^* ,q^* )=(2,4)$として、生成してみましょう。
k_true = 2.0
q_true = 4.0
gp1 = lambda x : gamma_pdf(x, k_true, q_true)
smp1 = PlainSampler(gp1, 0, 50, 1000)
h1 = plt.hist(smp1, bins=50)
showPdf(gp1, 0, 50, 100, h1[0].sum()/(h1[1][1]-h1[1][0]))
plt.show()
関数showPdfの行では、ヒストグラムと確率分布のY軸を合わせるための調整係数を掛けています。
データsmp1が観測値で、そのヒストグラムはこのようになります。当然、乱数で生成しているので実行するたびにヒストグラムの形状は変化します。
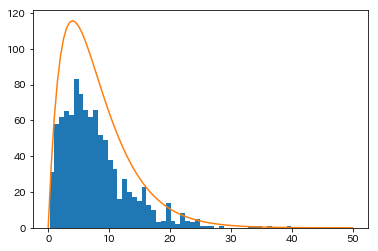
3. MCMC用の関数を準備
MCMCの計算に使う関数を定義していきます。
まず、事後確率分布$P(D_n |\theta)$を計算する関数です。確率計算値が小さくなりすぎるのを防ぐのと、データの独立性を確保するために、50個のサンプル値を元サンプルからさらに選んで同時確率$P(D_n |\theta)=P(X_1 | \theta)P(X_2 | \theta) \cdots P(X_n | \theta)$を計算しています。
def pdf_gamma_sample(x, sample):
k = x[0]
q = x[1]
# Pが小さく成りすぎるのを防ぐ
sample1 = np.random.choice(sample, 50)
p = [gamma_pdf(s, k, q) for s in sample1]
return np.prod(p)
パラメータ$\theta=(k,q)$の事前分布(初期分布)を与える関数です。事前情報がないため、一様乱数から生成することにしましょう。ただし、最大値だけ与えることにします。
def genInit( cdim, xdim, xmax):
x = np.random.rand(cdim, xdim)*xmax
return x
次が核となる部分です。Metropolisアルゴリズムによる写像$\pi(x \rightarrow x')$と、MCMCを実行する関数です。
def MHmap(pdf, x, xdim, sig):
# Gibbs サンプリング(1変数のみ変更)
xnew = x + np.eye(1, xdim, np.random.randint(xdim))[0,:] * np.random.normal(loc=0, scale=sig)
# xの値域を限定する
xnew = np.maximum(xnew, 0.01)
# Metropolis 基準で選択
r = np.random.rand()
if r < pdf(xnew)/pdf(x):
x = xnew
return x
def MCMC_gamma_01(sample, x0, sig, N):
#
pdf1 = lambda x: pdf_gamma_sample(x, sample)
#
x = x0
xs = []
for i in range(N):
# Metropolis基準に従って点群を写像
x = [MHmap(pdf1, e, 2, sig) for e in x]
# ランダムに再サンプリング
s = np.random.randint(0,len(x),(len(x)))
x = [x[j] for j in s]
#
xs.append(x)
return np.array(xs)
コーディングしたときのポイントです。
- Gibbs サンプリングを使う(たぶん使わなくてもよい)
- 遷移関数$Q(x,x')$は標準偏差$\sigma$の正規分布を使う
- 変数xの値域を限定する(負の領域に飛んでいかないように)
- πで写像したあとに、さらに再サンプリングする(理論上はしなくていいはずですが、あまりに遠くに飛んだ点がなかなか戻ってこない可能性を削減したいので)
この実装が最適かどうかは、正直良くわかりませんが、実際のライブラリ(PyMC3, WinBUGSなど)では、さぞかしもっと色々な工夫がなされているであろうことが想像できます。理論と実装の間にあるギャップが見えてくる部分です。
4. MCMCしてみる
では、2で作った観測データsmp1から、ガンマ分布モデルのパラメータ$\theta=(k,q)$を推定すべく、3で作った関数でMCMCしてみましょう。
点群のサイズを500、パラメータの次元は2次元、最大値は10としておきます。また、遷移関数$Q(x,x')$の標準偏差を3とします。MCMCの計算を100回行います。
p0 = genInit( 500, 2, 10)
sig = 3
xs = MCMC_gamma_01(smp1, p0, sig, 100)
数分経過すると結果が出てくるので、グラフにしてみます。
fig = plt.figure()
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
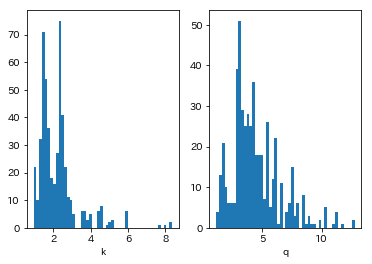
ax1.hist(xs[-1,:,0], bins=50)
ax2.hist(xs[-1,:,1], bins=50)
ax1.set_xlabel("k")
ax2.set_xlabel("q")
k_est = xs[-1,:,0].mean()
q_est = xs[-1,:,1].mean()
print("k*:{}, q*:{}".format(k_est, q_est))
plt.show()
結果が下図です。あまり綺麗なヒストグラムではありませんが、平均値で計算すると、$(\bar{k}, \bar{q})=(2.21, 4.46)$となりました。
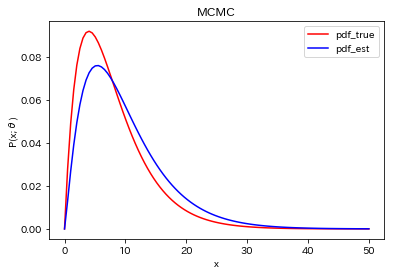
元の生成分布と$(\bar{k}, \bar{q})=(2.21, 4.46)$を使った分布を比較すると下図のようになりました。ちょっとずれてますが、裾の長い分布をまあそれなりに合わせることができるようです。
5. 他の結果
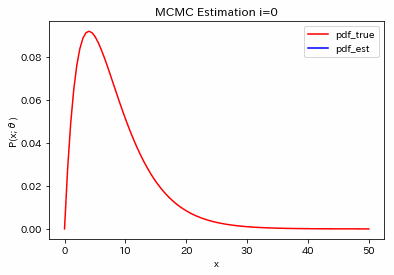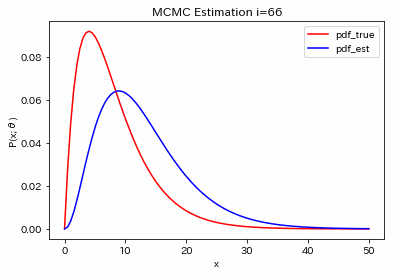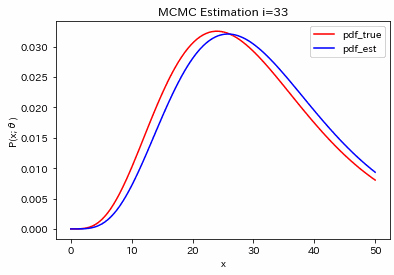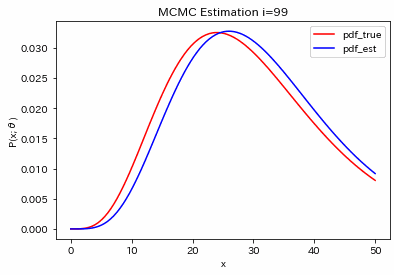
パラメータ$\theta=(k,q)$を色々と変えて試してみると、それなりに合うようです。大体100回くらい繰り返すと収束するような印象です。
考察
以上から、MCMCを素朴に実装してみて、ガンマ分布の推定してみた結果から次の傾向が見られました。
- ガンマ分布から生成した観測データを使って、元のガンマ分布のパラメータをサンプル平均値から(ある程度)推定することは可能。
- ただし、MCMCに与える事前分布としての初期分布や遷移関数$Q(x,x')$(の分散)に依存する傾向があった。
- ガンマ分布という非線形性の強い関数に使える点、パラメータの次元が高くても原理的には使える点、で有用そう。
さらに言えば・・・
- データ$D_n$からモデルに基づいて確率比を計算する部分は、非常に素朴に書きましたが、確率が非常に小さく成る場合の対策や高速化など色々工夫できそうです。
- 点群としてばらまいたサンプル集合の背後にある確率分布を推定する、というのは何だか光の粒子性と波動性に似ている気がして、関連があるような気がしますね。
- 確率分布が時間変化する場合などでどうなるか?も興味深いですね。
参考リンク
下記のページを参考にさせて頂きました。