この記事に関して
ここでは量子アニーリングの計算モデルの一つである、イジングモデル(Ising model)について説明します。
イジングモデル
イジング模型とは二つの状態をとる格子点から構成され、最隣接する格子点のみの相互作用を考えた格子模型を表しています。
難しい説明ですが、とりあえず図は以下のようになります。
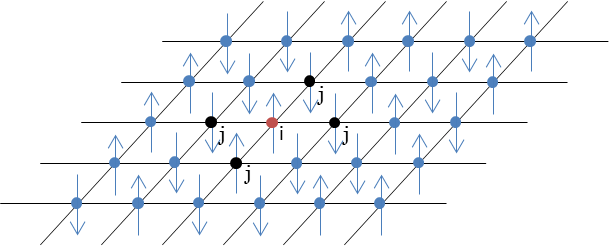
https://stat.ameba.jp/user_images/20170329/16/trite-note/e0/56/p/o0609024713901077207.png?caw=800
このように上と下の2つの状態が格子状に並んでいて各点は隣接した点(上の場合は4点)のみ何かしら相互作用が起こるようなモデルのことを言います。
一次元 Ising 模型(古典)
今回は上の図の横線1本のみ考えます。(一次元)
(つまり線分上に一定の間隔で点が置いている。)
この横線全てにかかるエネルギーを $H$ とすると、式は以下のようになります。
H = -\sum_{i < j}^{}J_{ij}\sigma_i \sigma_j \ , \ (\sigma_i \in \{\pm 1\})\\
J_{ij} = \left\{\begin{array}{cc} J & (i,j が隣接) \\ 0 & (i,j が隣接してない) \end{array} \right.
$H$ をハミルトニアンと言います。
式から上向きを $1$、下向きを $-1$ として、隣接したところでは相互作用 $J$ が働くことがわかります。
上の式から、隣接した点において、
| $\sigma_i$ | $\sigma_j$ | $J_{ij}\sigma_i\sigma_j$ |
|---|---|---|
| $1$ | $1$ | $J_{ij}$ |
| $1$ | $-1$ | $-J_{ij}$ |
| $-1$ | $1$ | $-J_{ij}$ |
| $-1$ | $-1$ | $J_{ij}$ |
| このことから同じ向きならエネルギーが下がり、違う向きならエネルギーが増加することがわかります。 |
$J_{ij}$ の定義からしばしば以下のようにも書かれます。
H = -J\sum_{\left< i,j \right>}^{}\sigma_i \sigma_j
ここで $\left< i,j\right>$ とは $i,j$ が隣接しているところを意味しています。
周期境界条件
上の場合は直線上なので端は繋がっていませんが、もし繋がっているとすると
$\sigma_{i+N} = \sigma_i$ より、上の式は
H = -J\sum_{i}^{N}\sigma_i \sigma_{i+1}
このように書き直せます。(N番目で元に戻る。)
この $\sigma_{i+N} = \sigma_i$ を周期的境界条件といいます。(線分の端を繋げて円にする。)
横磁場 Ising 模型(TFIM)
横磁場 Ising 模型は以下のようになります。
H = -\sum_{i < j}^{}J_{ij}\sigma_i \sigma_j - h\sum_{i}^{}\sigma_i\\
J_{ij} = \left\{\begin{array}{cc} J & (i,j が隣接) \\ 0 & (i,j が隣接してない) \end{array} \right.
$h$ は実数です。
このように一次の項があるイジング模型を横磁場 Ising 模型と言います。
一次元 Ising 模型(量子)
以上の流れを量子力学で考える。
H = -\sum_{i < j}^{}J_{ij}Z_i Z_j \\
J_{ij} = \left\{\begin{array}{cc} J & (i,j が隣接) \\ 0 & (i,j が隣接してない) \end{array} \right.
$Z_i$ は $i$ 番目にかかる Z ゲートで
Z_i = I \otimes \cdots \otimes I \otimes \overset{i}{Z} \otimes I \otimes \cdots \otimes I
= \bigotimes_{i>j}^{}I \otimes Z \bigotimes_{i<j}^{}I
のことです。
横磁場 Ising 模型(TFIM)
横磁場 Ising 模型は以下のようになります。
H = -\sum_{i < j}^{}J_{ij}Z_i Z_j - h\sum_{i}^{}X_i\\
J_{ij} = \left\{\begin{array}{cc} J & (i,j が隣接) \\ 0 & (i,j が隣接してない) \end{array} \right.
古典のときの一次の項が $X$ ゲートになります。
$Z$ ゲートは $\left|0\right>,\left|1\right>$ のような上下から成り立つ状態が固有ベクトルに対し、
$X$ ゲートは上の状態を重ね合わせた $\left|+\right>, \left|-\right>$ を固有ベクトルとします。
bloch 球でわかる通りこれは横向きなので横磁場と呼ばれます。
解法
イジングモデルのあらゆる量を考えるときに分配関数が基準となります。
この分配関数について説明していきます。
古典状態
まずは1次元上で考えます。( $H$ は行列ではない。)
分配関数
上のハミルトニアンについて
温度 $T$ のときに、$H(\sigma)$ を持つ配置 $\sigma$ が出る確率は
p(\sigma) = \frac{1}{Z} e^{-\beta H(\sigma)} \ \ \ (\beta = \frac{1}{k_B T})
これをボルツマン分布といい、$e^{-\beta H(\sigma)}$ をボルツマン因子といいます。
全ての確率の和は $1$ なので、
\sum_{\sigma}^{}p(\sigma) = 1
となります。
よって、$Z$ は以下のように定義できます。
Z = \sum_{\sigma}^{}e^{-\beta H(\sigma)}
この $Z$ を分配関数と言います。( Z ゲートではない。)
このとき、$H(\sigma)$ の期待値を $\langle H(\sigma) \rangle$ とすると、
\langle H(\sigma) \rangle = \sum_{\sigma}^{}H(\sigma)p(\sigma) = \frac{\sum_{\sigma}^{} H(\sigma) e^{-\beta H(\sigma)}}{\sum_{\sigma}^{} e^{-\beta H(\sigma)}} = -\frac{\partial}{\partial \beta}\log Z(\beta)
量子状態
次は量子力学上での振る舞いを考えます。
ハミルトニアン $H(\sigma)$ を行列として、固有値を $E_i(\sigma)$、固有ベクトルを $\left|\psi_i(\sigma)\right>$ とします。
( $E_0(\sigma) ≦ E_1(\sigma) \cdots ≦ E_n(\sigma)$ )
分配関数
上のハミルトニアンについて
配置 $\sigma$ に対し、温度 $T$ のとき $E_i(\sigma)$ を持つ確率は
p_i(\sigma) = \frac{1}{Z} e^{-\beta E_i(\sigma)} \ \ \ (\beta = \frac{1}{k_B T})
上と同様に考えると分配関数は
Z = \sum_{i}^{}e^{-\beta E_i(\sigma)}
このとき古典力学的期待値は
\langle H(\sigma) \rangle = \sum_{i}^{}E_i(\sigma)p_i(\sigma) = \frac{\sum_{i}^{} E_i(\sigma) e^{-\beta E_i(\sigma)}}
{\sum_{i}^{} e^{-\beta E_i(\sigma)}} = -\frac{\partial}{\partial \beta}\log Z(\beta)
と上と同じようにかけます。
また、$\left<\psi_i(\sigma)\right|H(\sigma)\left|\psi_i(\sigma)\right>$ は量子力学的期待値です。
一般にこの二つの値について
\left|\Psi(\beta)\right> = e^{-\frac{\beta}{2} H(\sigma)}\sum_{i}^{}\left|\psi_i(\sigma)\right>
と置くと、
\langle\Psi(\beta) \| \Psi(\beta)\rangle = \sum_{i,j}^{}
\left<\psi_i(\sigma)\right|
e^{-\beta H(\sigma)}
\left|\psi_j(\sigma)\right> =
\sum_{i}^{}
\left<\psi_i(\sigma)\right|
e^{-\beta H(\sigma)}
\left|\psi_i(\sigma)\right> =
\sum_{i}^{}e^{-\beta E_i(\sigma)} = Z(\beta)
より、
\langle H(\sigma) \rangle =
\frac{\left<\Psi(\beta)\right|H(\sigma)\left|\Psi(\beta)\right>}
{\langle\Psi(\beta) \| \Psi(\beta)\rangle}
という関係が成り立ちます。
まとめ
今回は イジングモデル について説明しました。
次回は 量子アニーリング について説明しようと思います。
参考文献
ホロノミック量子場 神保道夫 岩波書店
ボルツマン分布
https://ja.wikipedia.org/wiki/%E3%83%9C%E3%83%AB%E3%83%84%E3%83%9E%E3%83%B3%E5%88%86%E5%B8%83
ニューラルネットワークの理論1:イジングモデルの平均場近似解
https://ameblo.jp/trite-note/entry-12260856781.html
量子アニーリングの数理
https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/189516/1/bussei_el_033203.pdf
物理量を表す演算子
http://www.phys.cs.is.nagoya-u.ac.jp/~tanimura/class/H28-tanimura-quantum3.pdf
【分配関数】Zの意味。例を使って確率と期待値を求める。
https://batapara.com/archives/19092119.html/
分配関数とトレースの関係Z=Tr(exp(-βH))=Σexp(-βEk)の証明
https://batapara.com/archives/19115592.html/