PythonControlで矩形波に対する応答を求める。

目的

Python Controlで、1自由度系(バネマスダンバ系)の伝達関数の任意の矩形波に対する応答を求める。

事前準備

PythonControlをインストールする

システムのモデル化

以下の伝達関数について考える。

G(s)=\frac{Y(s)}{U(s)}=\frac{1}{ms^2+cs+k}

m:質量[kg]
k:ばね定数[N/m]
c:粘性減衰係数[N・s/m]
f：力[N]

Python Controlでの任意入力応答

Python Controlは任意の入力に対する応答は以下の関数で求めることができる。

control.matlab.lsim(sys, U=0.0, T=None, X0=0.0)

• Parameters:
  
  • sys:LTIシステム(線型時不変システム)の状態空間or伝達関数
  • U:各時刻での入力配列（デフォルト= 0）。UがNoneまたは0の場合、特殊なアルゴリズムが使用されます。この特別なアルゴリズムは、他の方法で使用される一般的なアルゴリズムより高速です。
  • T:時刻配列。数値は単調増加しなければなりません。
  • X0: 初期値(default=0)、数値は配列に自動変換。

control.matlab.lsimは線形システムの任意の応答を求めることができる。
パラメータU、X0の便宜として、数値(スカラー)は正しい形状の行列に変換されます。
正しい行列は、引数sysとTから推測されます。

引用元：
control.matlab.lsim

矩形波

矩形波は、numpyの関数を使用して、以下の関数で生成できる。

u = np.sign(amp*np.sin(2*np.pi*freq*t))

• Parameters
  • np.pi:円周率
  • freq：矩形波の周波数
  • t：時刻配列

サンプルコード

responce_lsim_quad.py

#!/usr/bin/env python
from control.matlab import *
from matplotlib import pyplot as plt
from scipy import arange 
import numpy as np

def main():
    k=1.0
    m=0.1
    c=0.1
    num = [0, 0,1] 
    den = [m, c, k]
    x0 = [0, 0]             
    t =np.linspace(0, 10, 1024) 
    freq=1.0    
    amp=1.0
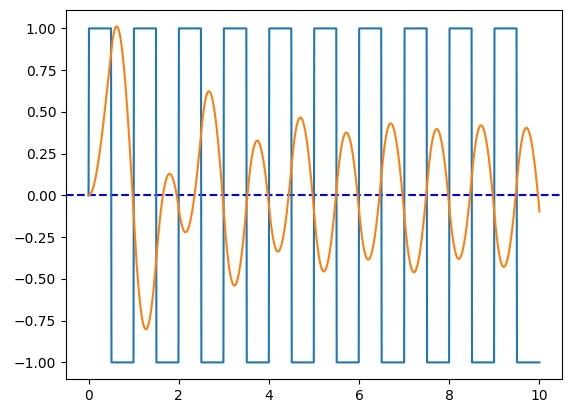
    u = np.sign(amp*np.sin(2*np.pi*freq*t)) 

    sys1 = tf(num, den)         
    print sys1

    (y1a, T1a, x1a )= lsim(sys1, U=u, T=t, X0=x0)

    plt.axhline(0, color="b", linestyle="--")
    plt.plot(T1a, u, label="$X_2$")
   # plt.plot(T1a, x1a[:,1], label="$X_1$")
   # plt.plot(T1a, x1a[:,0], label="$X_2$")
    plt.plot(T1a, y1a, label="Output")
    plt.show()

if __name__ == "__main__":
  main()

サンプルコードは以下に格納。
https://github.com/nnn112358/python-control_test

参考

PythonControlをインストールする
PythonControlで1自由度系の伝達関数を求める。
PythonControlで2自由度系の伝達関数を求める。